形状误差评定

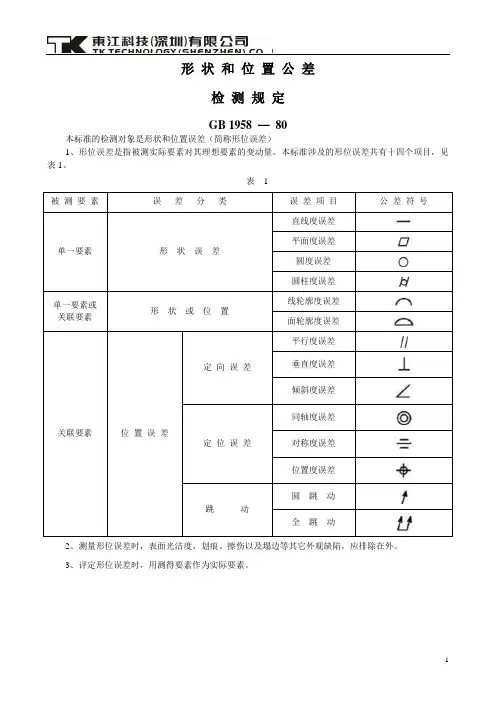
光学自由曲面面形误差评定光学自由曲面面形误差评定是光学工业中非常重要的一项技术任务，其目的是对制造的光学自由曲面进行精确的测量和评估，以确保光学系统的性能和质量满足设计要求。

在进行光学自由曲面面形误差评定之前，我们首先需要了解什么是自由曲面面形误差。

自由曲面是没有旋转对称性的曲面，其形状可以是二次曲线、非旋转对称的非二次曲面或复杂曲率曲面。

面形误差是指光学自由曲面与理想曲面之间的形状偏差。

这种形状偏差可能会导致光学系统的成像质量下降，因此我们需要对其进行准确的评定。

光学自由曲面面形误差的评定方法可以分为直接测量法和间接评定法。

直接测量法主要包括干涉测量法、光栅测量法和轮廓测量法等。

干涉测量法是其中最常用的方法之一，它基于干涉现象来测量光学自由曲面的形状误差。

光栅测量法则利用光栅的光学特性对曲面形状进行测量。

轮廓测量法则是通过测量曲面上一系列截面的形状来评定整个曲面的形状误差。

这些直接测量法能够提供高精度的测量结果，但对于复杂的曲面形状可能会存在一定的困难。

间接评定法则是通过测量光学自由曲面的光学性能来推断其面形误差。

常见的间接评定法有相散法、波前传递函数法和光学薄片法等。

相散法通过测量光学系统的色差对曲面形状误差进行评定。

波前传递函数法则通过测量光学系统的波前传递函数来评估光学自由曲面的面形误差。

光学薄片法则是通过在光学系统中插入不同厚度的光学薄片，观察其对成像质量的影响来推断曲面形状误差。

这些间接评定法相对直接测量法来说更加简便，但对于高精度的评定可能存在一定的局限性。

除了测量方法，光学自由曲面面形误差评定还需要考虑评价指标。

常用的评价指标有均方根误差（RMS）、PV值、直径误差等。

均方根误差是光学自由曲面实际形状与理想曲面之间的平均偏差的均方根值。

PV值则是曲面最高点与最低点之间的高差。

直径误差则是侧视图中曲面与理想圆的径向偏差。

不同的评价指标可以提供不同的面形误差信息，我们可以根据具体需求选择合适的评价指标。

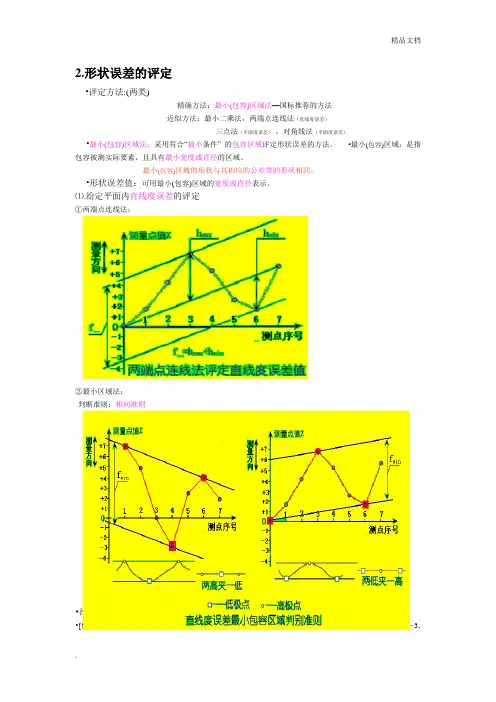
2.形状误差的评定•评定方法:(两类)精确方法：最小(包容)区域法—国标推荐的方法近似方法：最小二乘法，两端点连线法（直线度误差）三点法（平面度误差），对角线法（平面度误差）•最小(包容)区域法：采用符合“最小条件” 的包容区域评定形状误差的方法。

•最小(包容)区域：是指包容被测实际要素，且具有最小宽度或直径的区域。

最小(包容)区域的形状与其相应的公差带的形状相同。

•形状误差值：可用最小(包容)区域的宽度或直径表示。

⑴.给定平面内直线度误差的评定①两端点连线法：②最小区域法：判断准则：相间准则•给定平面内直线度误差评定的实例•[例4-1] 设用水平仪按下图所示测量某导轨的直线度，依次测得的各点读数分别为：－2, ＋1,－3,－3,＋3,＋1,－3,－2(单位为0.01mm)，试确定其直线度误差值。

解:因为水平仪是以水平面为基准测量后一点对前一点的相对高度差，所以首先应将测得的各点读数换算为对同一坐标系的坐标值，即将各点读数a i顺序累积,并取定原点(第0点)的坐标值h0＝0，则其余各点的坐标值：h i＝h i-1+ a i；计算结果如下表所列。

误差图形如下图所示。

按两端点连线方向作两平行包容直线(实线)包容误差图形，可得直线度误差值f_＝0 .06mm；若按最小包容区域法作两平行直线(虚线)包容误差图形，则直线度误差值f_ ＝0 .05mm。

[例4－2]如下图，用“打表法”测量一方条形零件上表面在某一给定垂直面V内的直线度误差。

依次测得五个点的读数为：－2，＋2，0，－1，＋1；（单位均为：µm），试求其直线度误差值。

解：①. 建立坐标系，绘出“误差折线” ；② .作最小区域,量取误差值:f min=3.7 µm；③. 作平行于两端点连线的包容区域,量取误差值: f_= 4.6 µm。

⑵. 平面度误差的评定•如右图所示,检测平面度误差时,一般先在被测平面上等间隔地布置3×3，或4 ×4，或5 ×5，…，然后，用指示表、水平仪等测量各点相对于基准点的读数。

圆度误差评定一、引言圆度误差评定是机械制造和测量技术中的一个重要概念，它涉及到对圆柱体或旋转体的圆周形状精确度的评价。

在实际生产过程中，由于受到多种因素的影响，零件的圆周形状往往存在一定的误差。

为了确保零件的准确性和可靠性，对其进行圆度误差评定是必不可少的。

本篇文章将围绕圆度误差评定的方法、标准及其实际应用进行详细探讨。

二、圆度误差评定方法圆度误差评定主要采用间接测量和直接测量两种方法。

间接测量是通过测量圆周上不同位置的高度差来评定圆度误差，这种方法适用于大型旋转体的测量。

直接测量则是通过测量圆周上若干点的半径值，利用数学模型计算出圆度误差，这种方法在小型零件的测量中较为常见。

1.间接测量方法：利用大直径测量装置，如大直径千分尺、大直径卡尺等，对大型旋转体的不同高度进行测量，根据测量数据计算出圆度误差。

这种方法对设备的要求较高，但测量精度相对较高。

2.直接测量方法：通过精密测径仪、光电显微镜、轮廓仪等高精度测量设备，直接测量小型零件在不同角度下的半径值。

然后利用最小二乘法、三点圆法等数学模型计算出圆度误差。

这种方法对设备的要求相对较低，但在测量大型旋转体时受到限制。

三、圆度误差评定标准为了统一评价零件的圆度误差，国际上制定了一系列的标准和规范。

其中，最为广泛采用的是ISO 5755《圆度和圆柱度误差检测》标准。

该标准规定了圆度和圆柱度误差的定义、评定方法、允许误差等基本要求。

此外，根据不同行业和具体应用需求，还制定了相应的国家和行业标准。

在ISO 5755标准中，圆度和圆柱度误差的评定主要采用最小二乘法、三点圆法等数学模型进行计算。

最小二乘法是以所有测点的半径值拟合出一个最小偏差圆的圆心位置和半径值，以此作为零件的圆度误差。

三点圆法则是选取三个不同的角度下的测点，计算其半径值后构成一个理想圆，该圆的圆心位置和半径值即为零件的圆度误差。

为了确保评定结果的准确性，进行圆度误差评定时需要遵循一定的原则：1.多次测量：对同一零件进行多次测量，以提高结果的可靠性和精度。

公差配合与测量技术| 98 |5种原则描述如下。

（1）与理想要素比较原则。

与理想要素比较原则是将被测实际要素与其理想要素相比较，用直接法或间接法测出其几何误差值。

实际测量中理想要素用模拟方法来体现。

如以平板、小平面、光线扫描平面作为理想平面；以刀口尺、拉紧的钢丝等作为理想的直线。

这是一条基本原则，大多数几何误差的检测都会应用这个原则。

（2）测量坐标值原则。

测量坐标值原则是测量被测要素的坐标值（如直角坐标值、极坐标值、圆柱面坐标值等），并经过数据处理获得几何误差值。

（3）测量特征参数原则。

测量特征参数原则是测量被测实际要素上有代表性的参数，并以此来表示几何误差值。

如图2-31所示，用两点法测量圆度误差值，其特征参数是直径，用指示表分别测出同一正截面内不同方向上的直径值，取最大直径与最小直径差值的一半，作为圆度误差。

按测量特征参数原则评定几何误差是一种近似的测量评定原则。

该原则检测简单，在车间条件下尤为适用。

（4）测量跳动原则。

测量跳动原则是将被测实际要素绕基准轴线回转，沿给定方向测量其对某参考点或线的变动量。

这一变动量就是跳动误差值。

如图2-32所示，用指示表测量径向圆跳动误差，当被测要素回转一周时，指示器的最大、最小读数之差，即径向圆跳动误差。

按上述方法测量若干个截面，取其跳动量最大的截面的误差作为该零件的径向圆跳动误差。

图2-31 利用特征参数测量圆度误差 图2-32 测量径向圆跳动（5）控制实效边界原则。

控制实效边界原则一般用综合量规来检验被测实际要素是否超出实效边界，以判断合格与否。

该原则适用于图样上标注最大实体原则的场合，即几何公差框格中标注的场合。

如图2-33所示，用综合量规测量两孔轴线的同轴度，综合量规通过被测零件，同轴度公差为合格。

图2-33 控制实效边界测量同轴度五、形状误差的检测（1）直线度误差检测（摘自GB/T 1958—2004《产品几何量技术规范（GPS ）形状和位置公差 检测规定》）见表2-3。

目录摘要 (3)前言 (3)第1章形状公差的概述 (4)1．1形状公差的概述 (4)1．2形状公差的定义 (6)第2章编程软件LabVIEW简介2．1 LabVIEW概述 (10)2．2 LabVIEW的应用 (10)2．3 LabVIEW的编程环境 (11)2．4设计过程中常用功能简介 (12)第3章形位误差的评定3． 1 直线度误差的评定 (21)第4章直线度检测系统设计4． 1 检测系统总体方案设计 (28)4．2 机械系统设计计算 (28)4．3 检测系统的硬件设计 (29)4．4 检测系统的软件设计 (31)附录 1 程序图 (37)参考文献 (38)摘要：本设计多功能形位误差测量仪，通过LABVIEW虚拟仪器控制采集与进行数据处理，通过多功能数据采集卡进行采集，使数据进入计算机中，采用不同的方法评定轴类零件的直线度、圆度和同轴度，然后可以得到它们的误差值和误差曲线图。

前言目前，生产现场对形位误差测试的要求不断提高，一些原有的测试手段已不能满足产品生产的需要。

例如各种工件的直线度的测量，以前采用跨桥和自准直仪测出角度，再采用人工计算、作图的方法得出结论。

这种方法存在两方面的不足：一是测量误差大、精度低。

如从自准仪上读数时要产生误差、人工画图时要产生误差；二是劳动强度大、效率低。

由于测量数据必须记录在表格中，再进行人工绘图，造成工作量大，耗费时间。

多功能形位误差测量系统是一种精度高、功能多、性能稳定、测量数度快、操作简单和使用方便的形位误差测量系统。

该系统可对直线度、圆度等形位误差进行测量，并且可以采用不同的方法进行评定误差。

第1章形状公差的概述1．1．概述零件在加工过程中，由于机床——夹具——刀具系统存在几何误差，以及加工中出现受力变形、热变形、震动和磨损等影响，使被加工的零件的几何要素不可避免地产生误差。

这些误差包括尺寸偏差、形状误差（包括宏观几何形状误差、波形和表面粗糙度）及位置误差。

形状误差检测1．直线度误差的检测方法一：光隙法将被测直线和测量基线（刀口尺、平尺）间形成的光隙与标准光隙相比较，直接评定直线度误差值。

此方法属直接测量，适用于磨削或研磨加工的小平面及短圆柱（锥）面的直线度误差测量。

例1：如图1a的图样标注，其检测方法如图1b所示。

将平尺或刀口尺与被测素线直接接触，并使平尺和被测素线间的最大间隙为最小，这个最大间隙就是被测素线的直线度误差。

测量若干条素线，取其中最大的误差值作为被测零件的直线度误差值。

平尺做得足够精确，可以作为直线的理想形状。

由于平尺的位置就是理想直线的位置，因此，测量时，应将平尺的位置放置符合最小条件，使平尺与被测素线间的最大间隙为最小，其方法如下：⑴若素线为两端高、中间低，即高-低-高时，如图2a所示。

平尺与两个高点相接触，则平尺与高点之间的间隙即为素线的直线度误差。

⑵若素线为两端低、中间高，即低-高-低时，如图2b所示。

平尺与最高点接触，并且使平尺与最低点的间隙相等，即f1=f2，此间隙就是素线的直线度误差。

方法二：垫塞法用量块或塞尺测量被测直线和测量基线之间的间隙，直接评定直线度误差值。

此方法属直接测量，适用于低精度被测零件的直线度误差测量。

方法三：指示器法（测微法）用带指示器的测量装置测出被测直线相对于测量基线的偏离值，进而评定直线度误差值。

此方法属直接测量，适用于中、小平面及圆柱、圆锥面素线或轴线等直线度误差测量。

例2：将被测零件放在平板上，并使零件紧靠直角座，在被测素线的全长范围内测量，同时记录读数，如图3中①所示。

根据记录的读数，用计算法按最小条件计算该条素线的直线度误差；将零件按图中②所示，间断旋转，重复上述步骤，测量若干条素线的直线度误差，取其中最大的误差值作为被测零件的直线度误差值。

例3：被测零件的图样标注如图4a所示，测量方法如图4b所示。

将被测零件安装在平行于平板的两顶尖之间，在开始端将两指示器调零后，沿铅垂轴截面的两条素线测量，如图4b中的①。