VAR模型应用案例完成

投资组合风险评估报告：VaR模型与应用I. 前言A. 引言B. 市场背景C. 目的和方法II. VaR模型介绍A. VaR的定义B. VaR的计算方法C. VaR的优劣势分析III. VaR模型的应用A. 投资组合风险评估1. 投资组合的概念与分类2. 投资组合的风险特征3. VaR模型在投资组合中的应用案例B. 风险管理与决策支持1. VaR模型在风险管理中的作用2. VaR模型在投资决策中的应用IV. VaR模型的局限性与扩展A. VaR模型的局限性1. 假设条件的不准确性2. 非线性风险的挑战3. 短期市场波动性的忽略4. 难以捕捉系统性风险B. VaR模型的扩展1. Historical VaR2. Monte Carlo VaR3. Conditional VaR4. Stress TestingV. VaR模型的实践与案例分析A. 金融市场中的VaR应用1. 证券投资组合的VaR评估2. 期货市场中的VaR风险分析B. 跨行业的VaR模型应用1. 制造业的VaR模型评估2. 零售行业的VaR风险控制VI. VaR模型在风险管理中的挑战与前景展望A. 流动性风险的考量B. 非线性风险的应对C. 模型的优化与改进D. 数字化技术的应用前景VII. 结论A. VaR模型在投资组合风险评估中的重要性B. VaR模型的应用前景与挑战C. 总结I. 前言A. 引言在投资组合管理中，风险评估是不可或缺的一环。

VaR模型作为一种常用的风险评估方法，在金融界得到了广泛应用。

本报告将详细介绍VaR模型的概念、计算方法及其在投资组合风险评估中的应用。

B. 市场背景随着金融市场的复杂性和波动性的增加，传统的风险评估方法已经无法满足投资者对风险敞口的需求。

VaR模型的应用能够更准确地评估投资组合的风险水平，有助于投资者制定更有效的风险管理策略。

C. 目的和方法本报告旨在系统地介绍VaR模型的原理与计算方法，并以案例分析的方式展示VaR模型在投资组合风险评估中的应用。

VAR案例分析范文
一、VAR案例分析
VAR，或“经济风险测量”，是用来度量经济实体暴露于金融风险的
一种常用方法。

它将交易风险和投资风险（由不确定的市场价格产生）组
合起来，以估计可能损失的潜在最大额度。

它并不是一种单独的工具，而
是一系列工具和系统，可以帮助金融机构识别和评估风险，以便做出准确
的商业决策。

本文将分析一个关于VAR的案例，以了解它的应用价值。

案例：银行希望使用VAR技术来改进其风险管理进程。

1.分析目标：银行希望改进其风险管理进程，以便尽量减少潜在损失。

2.分析方法：VAR技术可以帮助银行改进其风险管理过程，以便识别
和评估风险。

它通过分析历史行为和当前情况，以预测未来可能发生的交
易风险和投资风险，以识别可能损失的最大值，并制定相关的风险管理措施。

3.分析步骤：
（1）分析现有的交易风险和投资风险，包括市场风险、信用风险、
流动性风险等；
（2）根据历史行为和当前情况，利用VAR技术来估计可能发生的最
大损失；
（3）根据VAR估计值，进一步针对不同的类型风险制定具体的风险
管理措施，以减少风险；
（4）定期对金融市场进行预警和监测。

VAR模型的原理及应用1. 引言VAR（Vector Autoregression）模型是一种常用的计量经济学模型，用于分析多个相关时间序列变量之间的动态关系。

VAR模型在宏观经济学、金融学、营销研究等领域具有广泛的应用。

本文将介绍VAR模型的原理以及其在实际应用中的一些特点和注意事项。

2. VAR模型的原理VAR模型是基于时间序列数据的统计模型，它假设各个时间序列变量之间存在互相影响的关系。

VAR模型的核心思想是用当前变量的过去值和其他相关变量的过去值来预测当前变量的值。

具体来说，VAR模型可以表示为如下形式：$$ X_t = \\alpha_1X_{t-1} + \\alpha_2X_{t-2} + \\cdots + \\alpha_pX_{t-p} +\\epsilon_t $$其中，X t表示当前时间点的变量向量，$\\alpha_1, \\alpha_2, \\cdots,\\alpha_p$是模型的参数，$X_{t-1}, X_{t-2}, \\cdots, X_{t-p}$表示过去几个时间点的变量向量，$\\epsilon_t$表示误差项。

VAR模型的核心在于确定模型的参数和滞后阶数p。

参数的估计可以使用最小二乘法、极大似然法等方法。

滞后阶数的选择可以通过信息准则（如赤池信息准则、贝叶斯信息准则）来确定，一般通过对比不同滞后阶数下模型的拟合优度。

3. VAR模型的应用VAR模型具有广泛的应用场景，以下是一些常见的应用情况：3.1 宏观经济学中的应用对于宏观经济学研究来说，VAR模型可以用于分析不同经济指标之间的关系，例如国内生产总值（GDP）、消费者物价指数（CPI）、货币供应量等。

通过建立VAR模型，可以研究这些宏观经济指标之间的因果关系、冲击传递效应等。

3.2 金融领域中的应用VAR模型在金融领域中的应用广泛，可以用于分析股市、汇率、利率等金融变量之间的关系。

通过构建VAR模型，可以研究金融变量之间的动态相关性、风险传染效应等。

多元时间序列模型实例1. 引言1.1 背景介绍多元时间序列模型是现代经济学中重要的分析工具，它能够有效地捕捉多个经济变量之间的互动关系和动态演变规律。

在实际应用中，多元时间序列模型被广泛运用于宏观经济预测、货币政策制定、金融风险管理等领域。

随着经济全球化和金融市场的不断发展，经济变量之间的关联性不断增强，传统的单变量时间序列模型已无法满足复杂的分析需求。

多元时间序列模型的研究和应用变得尤为重要。

本文将重点讨论VAR模型和VECM模型两种典型的多元时间序列模型，分析它们的原理、优缺点以及应用范围。

通过实例分析，我们将探讨这两种模型在实际经济数据中的应用效果和结果。

并对研究过程中的局限性进行分析，为未来研究提出展望。

通过深入探讨和研究多元时间序列模型，我们可以更好地理解经济变量之间的内在联系，为经济政策制定和风险管理提供更为准确和可靠的参考依据。

1.2 研究意义多元时间序列模型在经济学、金融学、环境科学等领域具有重要的应用价值。

通过对多元时间序列数据的建模分析，可以帮助研究者更好地理解变量之间的关系和内在规律，预测未来的发展走势，制定有效的政策和决策，促进经济社会的可持续发展。

多元时间序列模型可以用来分析经济系统中不同变量之间的相互影响和作用机制。

通过构建VAR模型和VECM模型，可以揭示变量之间的联动关系，帮助研究者更好地理解经济系统内部的运行机制，从而为制定政策提供科学依据。

多元时间序列模型还可以用来预测未来的发展趋势。

基于对历史数据的建模分析，可以得出一定的预测结果，为政府、企业和个人提供决策参考，减少不确定性因素的影响，提高决策的准确性和效益。

多元时间序列模型的研究具有重要的实践意义和理论意义，对于推动经济社会的发展和提高决策的科学性都具有重要的意义。

本文将通过实例分析，探讨多元时间序列模型在实际中的应用效果和局限性，为相关研究提供参考和借鉴。

1.3 研究对象研究对象是指在本研究中所关注和研究的主体或对象。

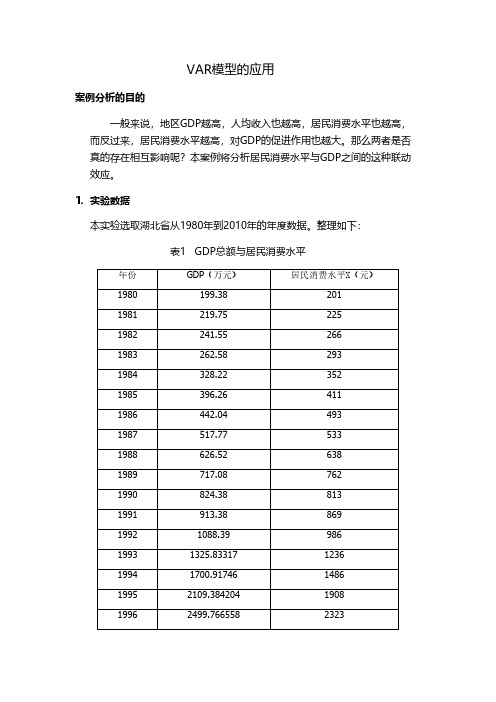
VAR模型的应用案例分析的目的一般来说，地区GDP越高，人均收入也越高，居民消费水平也越高，而反过来，居民消费水平越高，对GDP的促进作用也越大。

那么两者是否真的存在相互影响呢？本案例将分析居民消费水平与GDP之间的这种联动效应。

1.实验数据本实验选取湖北省从1980年到2010年的年度数据。

整理如下：表1 GDP总额与居民消费水平年份GDP（万元）居民消费水平X（元）1980199.382011981219.752251982241.552661983262.582931984328.223521985396.264111986442.044931987517.775331988626.526381989717.087621990824.388131991913.3886919921088.3998619931325.83317123619941700.91746148619952109.384204190819962499.766558232319972856.47035245919983114.015576257919993229.291593254520003545.392517268020013880.533733296220024212.82456326320034757.450974385320045633.24430920056590.19488320067617.47548020079333.46513200811328.927406200912961.17791201015967.6189773.VAR模型的构建3.1 数据平稳性检验因为数据变动趋势较大，本例对数据取对数，其中LGDP表示GDP总额，LX表示居民消费水平。

表2 将数据取对数调整后的新序列LGDP与LX年份LGDP LX1980 5.295213 5.3033051981 5.392491 5.41611982 5.487076 5.5834961983 5.570556 5.6801731984 5.793684 5.8636311985 5.982071 6.018593 1986 6.0914 6.200509 1987 6.249531 6.278521 1988 6.440181 6.458338 1989 6.575187 6.635947 1990 6.714632 6.700731 1991 6.817152 6.767343 1992 6.992455 6.893656 19937.1897967.119636 19947.4389237.303843 19957.6541517.553811 19967.8239537.750615 19977.9573427.80751 19988.0436687.855157 19998.0800187.841886 20008.1734047.893572 20018.2637287.99362 20028.3458898.090402 20038.4674678.256607 20048.636448.368461 20058.7933378.493515 20068.93828.60886 20079.1413558.781555 20089.3351148.91004620099.4697088.960725 20109.6783189.102421图1 居民消费水平与GDP的对数值的对比图图2 LX序列的单位根检验结果图4 LGDP序列的单位根检验结果从而LX和LGDP在5%的显著水平上均是平稳序列。

var模型r语言应用实例VAR模型是一种常用的时间序列分析方法，可以用来分析多个变量之间的相互关系。

R语言是一个功能强大的统计分析工具，可以用来实现VAR模型的建模和预测。

下面是一个VAR模型在R语言中的应用实例：假设我们有两个变量X和Y，它们之间存在某种关系。

我们可以使用VAR模型来建立它们之间的关系模型。

首先，我们需要导入数据并将其转换为时间序列对象：```R# 导入数据data <- read.csv('data.csv')# 转换为时间序列对象ts_data <- ts(data[,c('X','Y')], start=1, end=100, frequency=1)```然后，我们可以使用vars包中的VAR函数来建立VAR模型：```R# 导入vars包library(vars)# 建立VAR模型model <- VAR(ts_data, p=2)```在这个例子中，我们使用了滞后阶数p=2，这意味着我们考虑了前两个时期的影响。

接下来，我们可以使用predict函数来预测未来的值：```R# 预测未来10期的值forecast <- predict(model, n.ahead=10)```最后，我们可以使用plot函数来可视化预测结果：```R# 可视化预测结果plot(forecast)```以上就是一个简单的VAR模型在R语言中的应用实例。

通过VAR 模型，我们可以更好地理解多个变量之间的相互关系，并进行未来值的预测。

金融风险度量中的VaR模型解析引言：金融市场的复杂性和风险性注定了其对于风险度量的需求。

金融风险度量是金融机构和投资者在进行投资和管理资产时必备的工具，能够帮助他们了解和评估风险水平。

Value at Risk（VaR）模型是一种常见的金融风险度量模型，它通过对风险敞口的概率分布进行建模，计算出在给定置信水平下的最大可能损失额。

本文将对VaR模型进行解析，包括其定义、计算方法、模型假设、优缺点以及应用案例等内容。

一、VaR模型的定义VaR是Value at Risk的缩写，它被定义为在给定置信水平下可能发生的最大可能损失额。

VaR模型的核心思想是通过对风险资产或投资组合的概率分布进行建模，计算出在一定置信水平下的最大可能损失。

一般来说，VaR模型可以分为历史模拟法、参数法和蒙特卡洛模拟法等几种主要方法。

二、VaR模型的计算方法1. 历史模拟法：这种方法通过使用过去一段时期的历史数据来计算VaR。

具体而言，历史模拟法将过去的市场价格收益率作为未来市场价格收益率的概率分布，并根据所选的置信水平确定VaR。

这种方法的优点是简单易行，但缺点是没有考虑到市场条件的变化和不确定性。

2. 参数法：参数法使用统计模型对风险资产或投资组合的价格收益率进行建模，并基于这些模型计算VaR。

常见的参数法包括正态分布法、t分布法和GARCH模型等。

这种方法的优点是可以考虑到市场条件的变化和不确定性，但缺点是需要对概率分布的参数进行估计，估计结果的准确性对VaR的计算结果影响较大。

3. 蒙特卡洛模拟法：这种方法通过随机模拟未来市场价格的路径，并根据这些路径计算出未来的投资组合或风险资产的价值，并确定VaR。

蒙特卡洛模拟法的优点是能够模拟复杂的市场条件和不确定性，但缺点是计算复杂度较高，需要大量的计算资源。

三、VaR模型的假设1. 假设市场是有效的：VaR模型的计算基于市场价格收益率的概率分布，要求市场是有效的，即市场价格反映了所有可得到的信息。

多变量时间序列预测模型研究及应用随着各行各业的数据不断增长，如何有效地进行数据分析和预测成为了现代社会所关注的问题。

多变量时间序列（Multi-Variate Time Series，简称MVTS）预测模型是一种可以有效解决这个问题的方法。

本文将介绍该方法，以及其在实际应用中的重要性和可行性。

一、多变量时间序列预测模型概述所谓时间序列，指的是随着时间推移，数据以特定的顺序不断产生。

比如股票价格、气温、交通流量等等。

因为时间序列数据具有时序关联性，因此可以通过历史数据来预测未来趋势。

而所谓“多变量”，则是指在预测过程中，考虑了多个影响因素的情况。

比如，预测某城市未来一周的空气质量，可能需要考虑气象数据、交通拥堵状况、工厂排放情况等多个因素。

因此，多变量时间序列预测模型可以帮助我们更准确地预测未来。

传统的时间序列模型主要有AR、MA、ARMA、ARIMA等。

而MVTS模型则是在此基础上进行了扩展和改进，加入了多个过程变量或者多个之间变量的关系。

常用的MVTS模型有VAR、VECM、VARMA、VARX等。

VAR 模型（Vector Autoregression Model）是多变量时间序列模型中最常用的一种模型。

它是一种基于线性回归的方法，通过历史时间序列数据来预测未来一段时间的数据。

该模型并不依赖于特定的假设，因此在实际应用中有较广泛的适用性。

二、多变量时间序列预测模型的应用多变量时间序列预测模型在经济学、金融学、环境科学、气象学等领域都有着重要的应用。

下面将以几个实际案例来说明：1、经济学：以 GDP 和通货膨胀率为例，通过 VAR 模型预测未来几年的经济发展趋势。

同时，还可以考虑其他影响因素，比如政策变化、市场需求等。

这些因素的加入可以提高模型的预测准确度。

2、金融学：以股票价格为例，通过 VAR 模型预测未来股票的价格变化。

同时，可以考虑主要政策、市场需求等变量的影响。

通过这种方法，可以为投资者提供有用的决策参考。