(新六年级)圆环的面积练习题_

小学六年级圆环的练习题圆环是小学六年级数学学习中的重点内容之一。

通过练习圆环题目可以帮助学生巩固对圆环的认识和运用，提高数学思维和解题能力。

本文将为大家提供一些小学六年级圆环的练习题，以帮助学生更好地理解和应用相关知识。

1. 题目一：已知圆的半径为3cm，求其周长和面积。

解析：周长的公式为C=2πr，面积的公式为S=πr²。

将半径r=3cm 代入公式中计算即可得到结果。

周长C=2π×3≈18.85cm，面积S=π×3²≈28.27cm²。

2. 题目二：已知一个圆的周长为25.12cm，求其半径和面积。

解析：已知周长C=25.12cm，我们可以通过周长的公式推导出半径的计算公式r=C/(2π)。

将周长C=25.12cm代入计算可得半径r≈4cm。

接下来，我们可以通过半径的公式S=πr²求得面积S≈50.27cm²。

3. 题目三：一个圆的直径等于另一个圆的半径的两倍，如果小圆的周长为18.84cm，求大圆的周长和面积。

解析：我们设小圆的半径为r，由题意可知大圆的半径为2r。

已知小圆的周长C=18.84cm，我们可以通过周长的公式求得小圆的半径r≈3cm。

而大圆的半径为2r≈6cm。

再利用周长的公式C=2πr，我们可以求得大圆的周长C=2π×6≈37.7cm。

同样，根据面积的公式S=πr²，大圆的面积S=π×6²≈113.1cm²。

4. 题目四：已知一个圆的周长与直径的比值为π，求其半径和面积。

解析：已知周长与直径的比值C/d=π，我们可以推导出周长与半径的比值C/r=2π。

由于周长与半径的比值为常数，我们可以设周长为C，半径为r，则C/r=2π。

根据题意，可以得到周长C=r×2π，将此式代入C/r=2π中可得r×2π/r=2π，即2π=2π，该等式恒成立。

因此，我们无法求出具体的半径和面积。

六年级上册数学圆环的面积同步练习2一、选择题1．一个圆环的外圆半径是a厘米，内圆半径是b厘米，这个圆环的面积是（）平方厘米.A. πa2B. π（a2－b2）2．一个环形，内圆的半径是4cm，外圆的半径是5cm，下面计算圆环面积错误的算式是（）.（π取3.14）A. 3.14×52－3.14×42B. 3.14×（52－42）C. 3.14×（5－4）23．一座圆环形土楼，外圆半径是17米，内圆半径是7米，求这座土楼的占地面积，下面列式错误的是（）.（π取3.14）A. 3.14×（172-72）B. 3.14×（17-7）2C.3.14×172-3.14×724．一个环形铁片的外圆直径是10厘米，内圆直径是6厘米，求这个圆环的面积正确列式是（）.（π取3.14）A. 3.14×102-3.14×62B. 3.14×（10÷2）2-3.14×（6÷2）2C. 3.14×（10-6）25．一个圆环，它的外圆直径是内圆直径的两倍，则这个圆环的面积（）.A. 比内圆面积大B. 比内圆面积小C. 与内圆面积一样大D. 无法判断二、填空题6．一个环形垫圈的外圆半径是2厘米，内圆半径是1厘米，那么这个垫圈的面积是______平方厘米.7．一个环形铁片外圆直径是10分米，内圆直径是6分米，那么这个环形铁片的面积是______平方分米.8．某圆形滑雪场的直径是100米，经过均匀向外扩建，半径增加到60米，它原来的面积是______平方米，扩建后面积增加了______平方米.三、判断题9．圆环面积和外圆半径、内圆半径有关系.（）10．一个圆环，外圆直径是4米，内圆直径是2米，则圆环面积是37.68平方米.（）四、解答题11．在直径10米的圆形池塘的周围铺一条2米宽的小路，求路的面积是多少平方米.12．一个圆形花坛，直径为6米，沿花坛的周围修一条1米宽的小路.这条小路的面积是多少平方米？13．节假日里，明明在小区的广场坚持长跑，在广场中央的圆形喷水池的直径是20米，在水池的周围是一条宽10米的环形水泥路（如图）.这条水泥路的面积多少平方米？14．一个圆环的外圆半径是6cm，内圆的周长是15.7cm.这个圆环的面积是多少平方厘米？参考答案一、选择题1．B2．C3．B4．B5．A二、填空题6．9.427．50.248．7850 3454三、判断题9．✓10．×四、解答题11．路的面积是75.36平方米.12．这条小路的面积是21.98平方米.13．这条水泥路的面积是942平方米.14．这个圆环的面积是93.415平方厘米.答案第1页，共1页。

圆、圆环的面积一、单选题1.一个直径是6厘米的半圆，它的周长是( )厘米。

A. 9.42B. 15.42C. 18.842.一个小圆的直径等于一个大圆的半径，小圆面积是大圆面积的（）A. B. C. D.3.在比例尺是1：8的图纸上，甲、乙两个圆的直径比是2：3，那么甲、乙两个圆的实际的直径比是（）A. 1：8B. 4：9C. 2：3D. 1：44.在周长相等的长方形、正方形和圆中，（）的面积最大．A. 圆B. 长方形C. 正方形5.周长为800m的正方形铁片，要在其上截出一个圆，该圆最大面积是（）A. 100π平方米B. 1000π平方米C. 10000π平方米D. 100000π平方米6.有一个圆的周长是16πcm，那么这个圆的面积的一半是（）．A. 16πB. 32πC. 64πD. 128π7.圆的半径扩大3倍，它的面积扩大____倍．A. 3倍B. 6倍C. 9倍D. 12倍．8.在一个圆里面做一个最大的正方形，正方形和圆的面积比是( )。

A. 4：πB. 2：πC. π：2D. π：49.一个圆的面积是314平方厘米，它的半径是（）A. 1厘米B. 1分米C. 1米10.一个圆的半径扩大3倍，面积扩大（）倍．A. 3B. 6C. 9二、判断题11.(202X·甘肃岷县)小圆的直径是5厘米，大圆的直径是10厘米，那么大圆和小圆的面积比是2：1。

（判断对错）12.半径是2cm的圆的周长和面积相等。

13.（202X秋•罗平县期中）半圆的面积是圆面积的一半，半圆的周长也是圆周长的一半________．（判断对错）14.判断正误.圆A的半径是圆B的半径的3倍．那么，圆A的面积是圆B面积的6倍．15.在同一个圆中，圆心角的度数越大，扇形面积就越大．（判断对错）16.半径2厘米的圆，它的周长和面积相等．17.判断．一个圆的面积是以这个圆的半径为边长的正方形面积的π倍18.判断对错：圆的半径扩大2倍，面积也扩大2倍。

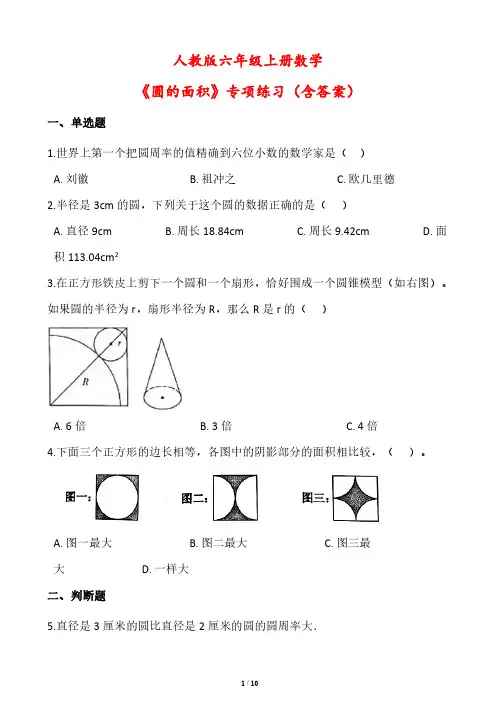
人教版六年级上册数学《圆的面积》专项练习（含答案）一、单选题1.世界上第一个把圆周率的值精确到六位小数的数学家是（）A. 刘徽B. 祖冲之C. 欧几里德2.半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm23.在正方形铁皮上剪下一个圆和一个扇形，恰好围成一个圆锥模型（如右图）。

如果圆的半径为r，扇形半径为R，那么R是r的（）A. 6倍B. 3倍C. 4倍4.下面三个正方形的边长相等，各图中的阴影部分的面积相比较，（）。

A. 图一最大B. 图二最大C. 图三最大 D. 一样大二、判断题5.直径是3厘米的圆比直径是2厘米的圆的圆周率大．6.一个圆的周长是它直径的π倍。

7.当圆的半径是2 cm时，它的周长和面积相等。

8.圆周长是直径的3.14倍．三、填空题9.圆的公式C=________=________，S＝________10.画一个直径是5厘米的圆，圆规两脚之间的距离是________厘米。

如果要画一个周长是12.56厘米的圆，圆规两脚之间的距离应该是________厘米，这个圆的面积是________平方厘米。

11.如图，把一个圆平均分成16份，剪开后拼成一个近似三角形，已知三角形的周长大约是19.14厘米，则圆的面积是________平方厘米。

12.在长8厘米，宽6厘米的长方形里面画一个最大的圆，圆的周长是________厘米，面积是________平方厘米。

13.把一个圆形纸片分成若干等份，然后拼成近似的长方形，量出长方形的长是15.7厘米，这个圆形纸片的面积大约是________。

四、解答题14.求下图阴影部分的面积。

（1）（2）（3）15.小明在纸上设计了一个图案（图中阴影部分），这个图案的面积是多少？五、应用题16.从一张正方形纸上剪下一个周长是18.84厘米的最大圆，求被剪掉的纸屑的面积。

参考答案一、单选题1.【答案】B【解析】【解答】世界上第一个把圆周率的值精确到六位小数的数学家是祖冲之。

第 2 课时
环形面积
作业很轻松，做做乐其中！
1．脑筋转转转，答案全发现。

(1)设C 为圆的周长，则C π×12
是( )。

A ．圆的半径 B ．圆的直径
C ．圆的周长
D ．圆的面积
(2)一个圆环，内圆半径是外圆半径的13
，这个圆环的面积是内圆面积的( )。

A.14 B ．3倍 C.19
D ．8倍 (3)圆的半径扩大到原来的6倍，它的面积( )。

A ．扩大到原来的6倍
B ．扩大到原来的12倍
C ．扩大到原来的36倍
D ．缩小到原来的16
2．求环形面积。

(1)R ＝1.5cm r ＝1cm
(2)r ＝0.6dm R －r ＝0.5dm
(3)大圆周长C ＝31.4cm r ＝2cm
3．一个环形机垫，外圆直径是9dm ，内圆周长是18.84dm ，这个机垫的面积是多少平方分米？
4．一个环形铁片，外圆直径是6dm ，环宽1dm ，这个环形铁片的面积是多少平方分米？
5．沿直径是6m 的圆形水池周围铺2m 宽的石子路，石子路的占地面积是多少平方米？
6．求阴影部分的面积。

不试不知道，一试真奇妙！求图中阴影部分的面积。

答案。

六年级圆环阴影面积练习题在六年级的数学学习中，圆环阴影面积是一个较为复杂的概念，需要学生进行充分的练习才能掌握。

本文将为大家提供一些六年级圆环阴影面积练习题，以帮助学生巩固知识，提升解题能力。

练习题1：在一个圆环中，内圆的半径为5cm，外圆的半径为8cm。

请计算圆环的阴影面积是多少。

解答：首先，我们计算内圆的面积和外圆的面积。

内圆的面积为π* 5² = 25π平方厘米，外圆的面积为π * 8² = 64π平方厘米。

然后，我们用外圆的面积减去内圆的面积，即可得到圆环的面积。

64π - 25π = 39π平方厘米。

所以，该圆环的阴影面积为39π平方厘米。

练习题2：一个圆环的内圆直径为10cm，外圆的半径为15cm。

请计算圆环的阴影面积是多少。

解答：首先，我们需要将内圆的直径转换为半径，即为5cm。

然后，计算内圆的面积和外圆的面积。

内圆的面积为π * 5² = 25π平方厘米，外圆的面积为π * 15² = 225π平方厘米。

最后，用外圆的面积减去内圆的面积，即可得到圆环的面积。

225π - 25π = 200π平方厘米。

所以，该圆环的阴影面积为200π平方厘米。

练习题3：一个圆环的内圆半径为4cm，外圆的周长为30cm。

请计算圆环的阴影面积是多少。

解答：首先，我们需要将外圆的周长转换为半径。

由于周长与半径的关系式为C = 2πr，即半径等于周长除以2π。

所以，外圆的半径为30/(2π) ≈ 4.77cm。

然后，计算内圆的面积和外圆的面积。

内圆的面积为π * 4² = 16π平方厘米，外圆的面积为π * 4.77² ≈ 71.66π平方厘米。

最后，用外圆的面积减去内圆的面积，即可得到圆环的面积。

71.66π - 16π ≈ 55.66π平方厘米。

所以，该圆环的阴影面积为55.66π平方厘米。

通过以上的练习题，相信同学们对六年级圆环阴影面积的计算有了更深入的了解。

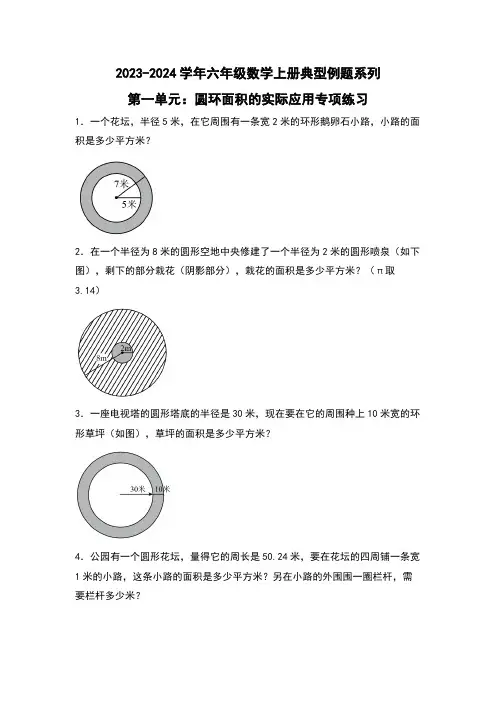
2023-2024学年六年级数学上册典型例题系列第一单元：圆环面积的实际应用专项练习1．一个花坛，半径5米，在它周围有一条宽2米的环形鹅卵石小路，小路的面积是多少平方米？2．在一个半径为8米的圆形空地中央修建了一个半径为2米的圆形喷泉（如下图），剩下的部分栽花（阴影部分），栽花的面积是多少平方米？（π取3.14）3．一座电视塔的圆形塔底的半径是30米，现在要在它的周围种上10米宽的环形草坪（如图），草坪的面积是多少平方米？4．公园有一个圆形花坛，量得它的周长是50.24米，要在花坛的四周铺一条宽1米的小路，这条小路的面积是多少平方米？另在小路的外围围一圈栏杆，需要栏杆多少米？5．一个圆形喷水池，半径8米，正中间有一个圆形小岛，半径6米。

这个喷水池的水面面积是多少平方米？6．一个圆形水池的半径是6米，在它周围用砖砌一条宽2米的小路，这条小路的面积是多少平方米？7．公园内有一个半径为3米的圆形水池。

现在要沿着水池的外边缘用地砖铺一条1米宽的小路，如果每平方米地砖30元，那么买地砖至少需要多少元？8．海滨公园中有一种“围树座椅”，形状如下图，这种“围树座椅”椅面的面积是多少平方米？9．公园里有一个周长是50.24米的花坛，现在要绕花坛周围铺上一条2米宽的水泥路，这条水泥路的面积是多少平方米？10．幸福村修建了一个周长是37.68米的圆形花坛，在花坛周围铺了一条2米宽的石子路，石子路的面积是多少平方米？每平方米植花25棵，每棵成本为4元，这条环形花带共需投资多少元？16．中心广场有一个圆形花坛，花坛外围是一条宽1米的石子路（如图）。

每天晚上小琳和爸爸妈妈都会绕着石子路的内侧（紧贴花坛）散步。

这天，走了1圈后计步器上显示步行了251.2米。

（1）这个圆形花坛的半径是多少米？（2）这条石子路的面积是多少平方米？17．园博园菊花展，有一个直径是40米的圆形花坛，要用大理石沿圆形花坛外围铺一条4米宽的小路。

如果每平方米按200元的费用计算，铺这条小路需要多少元？18．公园修建了一个直径为20米的圆形花坛。

第4课时 圆环的面积(教材例2，P68)一、我会填。

1．如图，阴影部分是一个( )。

它的外圆半径是R ，内圆半径是r ，这个阴影部分的面积是( )。

2．一个大圆的半径为5 cm ，一个小圆的半径为4 cm ，这两个圆的面积相差( )cm 2。

3．用一根长12.56 dm 的铁丝围成一个最大的圆，这个圆的面积是( )dm 2。

二、我会判断。

1．圆环的面积等于外圆的面积与内圆面积的差。

( )2．在一个大圆内剪去一个小圆，剩下的部分就是圆环。

( )三、看图计算阴影部分的面积。

(单位：cm ) 1.2.圆环是( )图形，它有( )条对称轴。

四、解决问题。

1．一个圆形水池，水池的中心有一个圆形小岛，求环形水面的面积。

(单位：米)2．一个圆形的水景坛的直径是100米，在它的周围修一条宽4米的公路，这个环形公路的面积是多少？3．白天鹅俱乐部有一个圆形舞池，周长37.68米，现准备周围加宽1米，这样舞池面积可增加多少平方米？五、如图，在半径为R 的圆形钢板上，除去半径为r 的四个圆，请列出阴影部分面积S 的计算式子，并计算当R ＝6 cm ，r ＝2 cm 时，S 的值。

口算 25×45＝ 0.875×314＝39×413＝ 13＋0.125＝ 0.5×15＝ 1÷79＝ 45÷25＝47÷67＝ 1115÷1115＝ 89÷23＝第4课时圆环的面积一、1.圆环π(R2－r2) 2.28.26 3.12.56二、1.√ 2.×三、1.3.14×(62－42)＝62.8(cm2) 2.16÷2＝8(cm)(82－52)×3.14＝122.46(cm2)四、1.3.14×(152－52)＝628(平方米)答：环形水面的面积是628平方米。

2.3.14×(100÷2＋4)2－3.14×(100÷2)2＝1306.24(平方米)答：这个环形公路的面积是1306.24平方米。

精品文档用心整理
第5单元圆
第6课时圆环的面积
一、填一填。

1.甲圆半径是乙圆半径的3倍，甲圆的周长是乙圆周长的（），甲圆面积是乙圆面积的（）。

2.在周长相等的长方形、正方形、圆中，（）面积最大。

3.用圆规画一个圆，如果圆规两脚之间的距离是7厘米，画出的这个圆的周长是（）厘米，这个圆的面积是（）平方厘米。

4.有大小两个圆，大圆直径是小圆半径的4倍，小圆与大圆周长的比是（），小圆与大圆面积的比是（）。

二、在一个面积80平方分米的正方形铁板上剪一个最大的圆，这个圆的面积是多少？
三、用铁皮剪成一个圆环，内圆半径4厘米，环宽2厘米，它的面积是多少？
资料来源于网络仅供免费交流使用。

北师大版六年级数学第一单元第三课
圆的环形面积专题(3.2)
姓名：班级：座位：家长签名：环形面积公式：S=∏×（R²-r²）
1.一个半径为3m的圆形花坛外，围绕一周修一条1m宽的小路，这条小路的面积是多少平方米？
2.街心花园里有一个半径为6m的圆形花坛，要在其周围修2m宽的水泥路，这条水泥路的面积是多少？
3.在一块直径为10米的圆形草地中间修一个半径为3米的圆形花坛，剩下的草地面积是多少平方米？
4.圆形花坛周围是一条环形的小路，花坛直径是4米，小路宽2米，这条环形小路占地多少平方米？
5.一个环形铁片，外圆直径0.4米，环宽0.1米，这个环形铁片的面积是多少平方厘米？
6.有一个圆环，外圆周长是62.8厘米，内圆周长是56.52厘米，圆环面积是多少平方厘米？。

北师大六年级数学上册圆环面积专题训练（含答案）
1.某师大附小在半径为120m的圆形跑道上举行自行车赛．六（1）班的刘明6分钟骑完两圈，他的自
行车的车轮直径是0.5m．刘明每分钟的车速是多少米？
2.一块圆形菜地原来的周长是18.84米，现在周围加宽2米，这块菜地的面积增加多少平方米？
3.圆形花圃的直径是7米，它的周围筑有篱笆，篱笆的周长是多少？
4.一个圆形花坛的周长是62.8米，若把它的直径增加2米，面积会增加多少平方米？
5.一个圆形羊圈的周长是31.4米．如果要扩建这个羊圈，把它的直径增加2米，羊圈的面积增加了
多少平方米？
6.在一个长12分米，宽5分米的长方形里剪去一个最大的半圆，这个半圆的面积是多少？
7.用一根铁丝围成一个长为5米，宽为2.85米的长方形．如果把这根铁丝围成一个圆形，求这个圆
的面积是多少？
8.一个圆的周长为25.12cm，先把它平均分成若干等份，再拼成一个近似长方形，长方形的周长是多
少厘米？
9.在比赛中，铅球投掷的落点区域是一个圆，如图，某运动员最远投掷距离为15m，铅球可能的落
点区域面积是多少？
3.14×152×
＝3.14×225×
＝176.625（m2）
答：铅球可能的落点区域面积是．
答案：
1. 3.14×120×2÷6＝125.6米
2. 50.24平方米
3. 21.98米
4. 6
5.94平方米
5. 34.54平方米
6. 39.25平方分米
7. 19.625平方米
8. 33.12厘米
9. 176.625平方米。

六年级上册数学书圆环的练习题圆环是数学中一个重要的概念，六年级上册数学书中也有大量的圆环练习题。

通过解答这些练习题，可以帮助学生巩固对圆环的理解与应用。

本文将针对六年级上册数学书中的圆环练习题进行分析和解答，旨在帮助学生更好地掌握这一知识点。

【第一题】已知圆环的外半径为10厘米，内半径为6厘米，求圆环的面积。

解析：根据数学书中给出的定义，圆环的面积可以通过以下公式来计算：面积= π × (外半径² - 内半径²)根据题目中给出的数据，我们可以将其代入公式进行计算：面积= π × (10² - 6²) = π × (100 - 36) = π × 64所以圆环的面积为64π平方厘米。

【第二题】已知一个圆环的外半径为8厘米，圆环的周长为40厘米，求圆环的内半径。

解析：首先，我们知道圆环的周长可以通过以下公式来计算：周长= 2π × 外半径+ 2π × 内半径根据题目中的数据，我们可以将其代入公式进行计算：40 = 2π × 8 + 2π × 内半径40 = 16π + 2π × 内半径2π × 内半径 = 40 - 16π内半径 = (40 - 16π) / 2π将π取近似值3.14代入计算：内半径 = (40 - 16 × 3.14) / (2 × 3.14)内半径 = (40 - 50.24) / 6.28内半径 = -10.24 / 6.28内半径≈ -1.63由于一个圆环的内半径不可能是负数，所以这个题目没有解。

【第三题】一个圆环的圆心角为120度，求这个圆环的弧长。

解析：根据数学书中的定义，圆心角所对的弧长可以通过以下公式来计算：弧长 = 圆心角 / 360度× 2π × 半径根据题目中给出的数据，我们可以将其代入公式进行计算：弧长 = 120 / 360度× 2π × 半径假设圆环的半径为r，代入数据进行计算：弧长 = 120 / 360度× 2π × r弧长= (1/3) × 2π × r弧长= (2/3)πr所以这个圆环的弧长为(2/3)πr。

小学六年级《圆的面积》练习题一.选择题(共6题，共12分)1.圆的半径是一条（）。

A.直线B.射线C.线段2.通过圆心并且两端都在圆上的（）叫做圆的直径。

A.射线B.线段C.直线3.一个半圆形，半径为r，它的周长为（）。

A. B.πr C.πr+2r D.π+r4.圆环的对称轴有（）条。

A.一B.无数C.无法确定5.车轮滚动一周，所行的路程是求车轮的（）。

A.周长B.半径C.直径6.一个圆的半径增加1厘米，它的周长就增加（）。

A.1厘米B.2厘米C.6.28厘米 D.3.14厘米二.判断题(共6题，共12分)1.在一个圆内，剪去一个扇形后，剩下的部分仍是扇形。

（）2.半径2厘米的圆的周长和面积是相等的。

（）3.通过圆心的线段叫做圆的直径。

（）4.6个圆心角都是60°的扇形一定可以拼成一个圆。

（）5.半径2米的圆，它的周长和面积是相等的。

（）6.半径为4cm的圆的周长是它面积的一半。

（）三.填空题(共8题，共16分)1.在一个周长是16米的正方形纸片内，剪下一个最大的圆，这个圆的周长是（）米。

2.一座台钟的钟面直径是10厘米，它的半径是（）厘米。

3.一个圆的半径是3厘米，这个圆的直径是（）厘米，周长是（）厘米。

4.三角形、四边形是直线图形，圆是（）图形；圆中心的一点叫做（），通过圆心，并且（）都在（）的线段叫做圆的直径；战国时期《墨经》一书中记载“圜（圆），一中同长也。

”表示圆心到圆上各点的距离都相等，即（）都相等。

5.用字母表示圆周长的公式是（）或（）。

6.大圆直径是小圆直径的3倍，大圆周长是小圆周长的（）倍。

7.如图，圆上A、B两点之间的部分叫做（），读作（）。

8.圆的周长是6.28米，则圆的直径是（）米，半径是（）米。

四.计算题(共2题，共12分)1.求阴影部分的面积。

2.求下图中阴影部分的面积。

（1）（2）五.作图题(共2题，共22分)1.按要求在方格纸上画图形。

（1）在方格纸上，把圆O向右平移4格，画出平移后的图形。