齿轮传动的载荷和应力

11-4直齿圆柱齿轮传动的作用力及计算载荷：一、齿轮上的作用力：为了计算齿轮的强度，设计轴和选用轴承，有必要分析轮齿上的作用力。

当不计齿面的摩擦力时，作用在主动轮齿上的总压力将垂直于齿面，（因为齿轮传动一般都加以润滑，齿轮在齿啮合时，摩擦系数很小，齿面所受的摩擦力相对载荷很小，所以不必考虑），即为P175图11-5b所示的Fn（沿其啮合线方向），Fn可分解为两个分力：圆周力：Ft=2T1/d1 N径向力：Fr=Fttgα N而法向力：Fn=Ft/cosα NT1：小齿轮上的扭矩 T1=9550000p/n1 n·mmP：传递的功率（KW） d1：小齿轮分度圆直径 mmα：压力角 n1：小齿轮的转速(r·p·m)Ft1：与主动轮运动方向相反；Ft2与从动轮运动方向一致。

各力的方向 Fr：分别由作用点指向各轮轮心。

Fn：通过节点与基圆相切（由法切互为性质）。

根据作用力与反作用力的关系，主从动轮上各对的应力应大小相等，方向相反。

二、计算载荷：Fn是根据名义功率求得的法向力，称为名义载荷，理论上Fn沿齿宽均匀分布，但由于轴和轴承的变形，传动装置的制造安装误差等原因，载荷沿齿宽的分布并不均匀，即出现载荷集中现象（如P176图11-6所示，齿轮相对轴承不对称布置，由于轴的弯曲变形，齿轮将相互倾斜，这时，轮齿左端载荷增大，轴和轴承刚度越小，b越宽，载荷集中越严重。

此外，由于各种原动机和工作机的特性不同，齿轮制造误差以及轮齿变形等原因，还会引起附加动载荷。

精度越低，圆周速度V越大，附加载荷越大。

因此在计算强度时，通常以计算载荷K·Fn代替名义载荷Fn，以考虑上两因素的影响。

K—载荷系数表达式11-311-5 直齿圆柱齿轮的齿面接触强度计算：一、设计准则：齿轮强度计算是根据齿轮失效形式来决定的，在闭式传动中，轮齿的失效形式主要是齿面点蚀，开式传动中，是齿轮折断，在高速变截的齿轮传动中，还会出现胶合破坏，因胶合破坏的计算方法有待进一步验证和完善。

齿轮传动的设计参数、许用应力与精度选择(一)齿轮传动设计参数的选择压力角α的选择由机械原理可知，增大压力角α,轮齿的齿厚及节点处的齿廓曲率半径亦皆随之增加，有利于提高齿轮传动的弯曲强度及接触强度。

我国对一般用途的齿轮传动规定的标准压力角为α=20°。

为增强航空用齿轮传动的弯曲强度及接触强度，我国航空齿轮传动标准还规定了α=25°的标准压力角。

但增大压力角并不一定都对传动有利。

对重合度接近2的高速齿轮传动，推荐采用齿顶高系数为1～1.2 ，压力角为16°～18°的齿轮，这样做可增加轮齿的柔性，降低噪声和动载荷。

小齿轮齿数 z1 的选择若保持齿轮传动的中心距 a 不变，增加齿数，除能增大重合度、改善传动的平稳性外，还可减小模数，降低齿高，因而减少金属切削量，节省制造费用。

另外，降低齿高还能减小滑动速度，减少磨损及减小胶合的可能性。

但模数小了，齿厚随之减薄，则要降低轮齿的弯曲强度。

不过在一定的齿数范围内，尤其是当承载能力主要取决于齿面接触强度时，以齿数多一些为好。

闭式齿轮传动一般转速较高，为了提高传动的平稳性，减小冲击振动，以齿数多一些为好。

小齿轮的齿数可取为 z1=20～40。

开式(半开式)齿轮传动，由于轮齿主要为磨损失效，为使轮齿不至过小，故小齿轮不宜选用过多的齿数，一般可取z1=17～20。

为使轮齿免于根切，对于α=20°的标准直齿圆柱齿轮，应取z1≥17。

齿宽系数φd的选择由齿轮的强度计算公式可知，轮齿愈宽，承载能力愈高；但增大齿宽又会使齿面上的载荷分布趋不均匀，故齿宽系数应取得适当。

圆柱齿轮齿宽系数的荐用值见下表。

对于标准圆柱齿轮减速器，齿宽系数取为，所以对于外啮合齿轮传动：。

φa的值规定为0.2,0.25,0.30,0.40,0.50,0.60,0.80,1.0,1.2。

运用设计计算公式时，对于标准减速器，可先选定φa后再用上式计算出相应的φd值。

133第11章 齿轮传动11.1考点提要11.1.1 重要的术语及概念软齿面、硬齿面、许用应力、弯曲疲劳强度、接触疲劳强度、接触应力、弯曲应力、点蚀、胶合、载荷系数、齿宽系数、齿形系数、应力集中系数、应力循环次数、齿轮精度等级。

11.1.2 许用应力的计算接触疲劳强度的许用应力为： HH HN H S K lim ][σσ= （11—1） 式中：HN K 称为寿命系数，由应力循环次数确定；lim H σ是齿面材料的接触疲劳极限；H S 为安全系数。

即使两齿轮采用同样的材料和热处理，由于两齿轮会有齿数不同，所以应力循环次数也就不同，从而导致寿命系数HN K 不同，因此许用应力也不同。

只有两齿轮齿数相同或齿数虽不同但都按无限寿命取相同的寿命系数HN K 并取相同的安全系数H S ，许用应力才相同。

弯曲疲劳强度的许用应力为：FFE FN F S K σσ=][ （11—2） 式中：环次数确定）为寿命系数（由应力循FN K ；FE σ为齿面材料的弯曲疲劳极限；F S 为安全系数。

即使两齿轮采用同样的材料和热处理，由于两齿轮会有齿数不同，所以应力循环次数也就不同，从而导致寿命系数FN K 不同，因此许用应力也不同。

如果两齿轮齿数相同或齿数虽不同但都按无限寿命取相同的寿命系数FN K 并取相同的安全系数F S ，许用应力才会相同。

为实现等强度设计，如果采用软齿面（HBS 350≤），一般小齿轮比大齿轮硬度高30-50HBS，小齿轮对大齿轮有冷作硬化作用。

如采用硬齿面（HBS 350>），在淬火处理中难以做到如此的硬度差，设计时按同样硬度设计。

要注意：如果是开式齿轮传动，则极限应力要乘以0.7，由于极限应力是按单向转动所获得的数据，如果是双向转动，则也要乘以0.7。

11.1.3齿轮的失效形式和计算准则齿轮的失效形式有五种：（1）轮齿折断。

减缓措施：增大齿根的圆角半径，提高齿面加工精度，增大轴及支承的刚度。

齿轮负载计算公式
齿轮负载计算公式通常用于确定齿轮传动系统中的负载能力。

具体的计算公式取决于所使用的齿轮类型和传动参数。

以下是一些常见的齿轮负载计算公式示例：
1. 弯曲应力法（Lewis公式）：
负载能力= 转矩/ (齿数* 齿宽* 应力修正系数)
2. 动载荷法（ISO 6336标准）：
负载能力= (功率* 1000) / (齿数* 齿宽* 齿轮模数* 齿宽系数* 传动效率)
3. AGMA公式（美国齿轮制造协会）：
负载能力= (齿数* 齿宽* 弯曲强度系数* 齿宽系数* 齿间载荷分布系数* 材料强度系数* 转矩) / (安全系数* 齿轮模数)
这些公式只是较常见的几种，实际的负载计算可能需要考虑更多因素，如齿轮材料、齿轮几何形状等。

对于具体的应用场景，建议参考相关的齿轮设计手册、标准或咨询专业工程师以获取准确的负载计算公式。

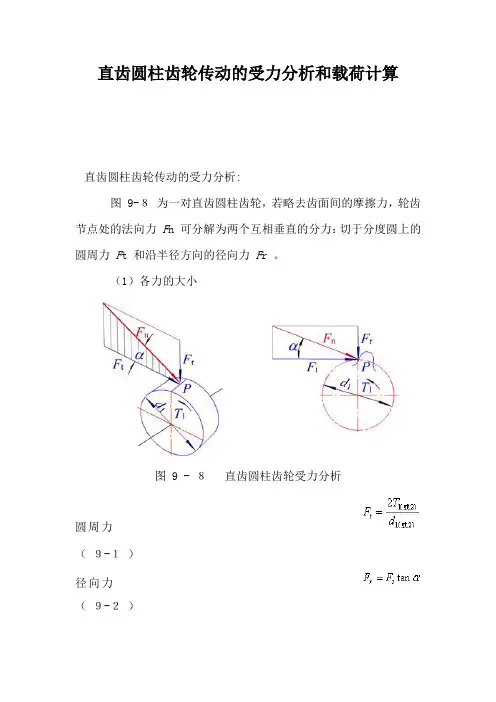
直齿圆柱齿轮传动的受力分析和载荷计算直齿圆柱齿轮传动的受力分析:图 9-８为一对直齿圆柱齿轮，若略去齿面间的摩擦力，轮齿节点处的法向力F n 可分解为两个互相垂直的分力：切于分度圆上的圆周力F t 和沿半径方向的径向力F r 。

（1）各力的大小图 9 - ８直齿圆柱齿轮受力分析圆周力（９-１）径向力（９-２）法向力（９-３）其中转矩（９-４）式中：T1 ，T2 是主、从动齿轮传递的名义转矩，N.mm ；d1 ，d2 是主、从动齿轮分度圆直径， mm ；为分度圆压力角；P是额定功率， kW ；n1 ，n2 是主动齿轮、从动轮的转速， r/min 。

作用在主动轮和从动轮上的各对应力大小相等，方向相反。

即：，，（2）各力的方向主动轮圆周力的方向与转动方向相反；从动轮圆周力的方向与转动方向相同；径向力F r 分别指向各自轮心 ( 外啮合齿轮传动 ) 。

9.4.2 计算载荷前面齿轮力分析中的F n 、F t 和F r 及F a 均是作用在轮齿上的名义载荷。

原动机和工作机性能的不同有可能产生振动和冲击；轮齿在啮合过程中会产生动载荷；制造安装误差或受载后轮齿的弹性变形以及轴、轴承、箱体的变形，会使载荷沿接触线分布不均，而同时啮合的各轮齿间载荷分配不均等，因此接触线单位长度的载荷会比由名义载荷计算的大。

所以须将名义载荷修正为计算载荷。

进行齿轮的强度计算时，按计算载荷进行计算。

（９－４）计算载荷(９ - ５)载荷系数(９- ６)式中：K是载荷系数；K A 是使用系数；K v 是动载系数；是齿向载荷分布系数；是齿间载荷分配系数。

1 ．使用系数K A使用系数K A 是考虑由于齿轮外部因素引起附加动载荷影响的系数。

其取决于原动机和工作机的工作特性、轴和联轴器系统的质量和刚度以及运行状态。

其值可按表 9 - ３选取。

表 9-３使用系数K A工作机的工作特性工作机器原动机的工作特性及其示例电动机、均匀运转的蒸气机、燃气轮机蒸气机、燃气轮机液压装置电动机（经多缸内燃机单缸内燃机（小的，启动转矩大）常启动启动转矩大）均匀平稳发电机、均匀传送的带式或板式运输机、螺旋输送机、轻型升降机、机床进给机构、通风机、轻型离心机、均匀密度材料搅拌机等1.00 1.101.251.50轻微冲击不均匀传送的带式输送机、机床的主传动机构、重型升降机、工业与矿用风机、重型离心机、变密度材料搅拌机、给水泵、转炉、轧机、1.25 1.351.51.75中等冲击橡木工机械、胶积压机、橡胶和塑料作间断工作的搅拌机、轻型球磨机、木工机械、钢坯初轧机、提升装置、单缸活塞泵等1.50 1.601.752.00严重挖掘机、重型球磨机、橡 1.75 1.85 2.0 2.25冲击胶揉合机、落沙机、破碎机、重型给水泵、旋转式钻探装置、压砖机、带材冷轧机、压坯机等0或更大注： 1. 对于增速传动，根据经验建议取表中值的 1.1 倍。

斜齿轮传动载荷计算公式斜齿轮传动是一种常见的机械传动形式，它通过两个斜齿轮的啮合来传递动力和转矩。

在工程设计中，计算斜齿轮传动的载荷是非常重要的，因为它直接影响到传动系统的工作性能和寿命。

本文将介绍斜齿轮传动载荷的计算公式及其应用。

斜齿轮传动的载荷主要包括两部分，弯曲载荷和接触载荷。

弯曲载荷是由于齿轮受到外部载荷作用而产生的变形和应力，而接触载荷则是由于齿轮啮合时产生的压力和摩擦力。

为了计算斜齿轮传动的载荷，我们需要先确定齿轮的几何参数和工作条件，然后应用相应的计算公式进行计算。

首先，我们来看弯曲载荷的计算。

斜齿轮的弯曲载荷可以通过以下公式来计算：Fb = (2T) / (d ym Z) 。

其中，Fb为齿轮的弯曲载荷（N），T为传动的转矩（N·m），d为齿轮的分度圆直径（m），ym为齿轮的模数修正系数，Z为齿轮的齿数。

接下来是接触载荷的计算。

斜齿轮的接触载荷可以通过以下公式来计算：Fc = (T cosα) / (d yz Z) 。

其中，Fc为齿轮的接触载荷（N），T为传动的转矩（N·m），α为齿轮的压力角（°），d为齿轮的分度圆直径（m），yz为齿轮的齿形修正系数，Z为齿轮的齿数。

最后，我们需要将弯曲载荷和接触载荷进行合成，得到斜齿轮传动的总载荷。

合成载荷的计算公式如下：Ft = √(Fb² + Fc²) 。

其中，Ft为齿轮的总载荷（N），Fb为齿轮的弯曲载荷（N），Fc为齿轮的接触载荷（N）。

通过以上公式，我们可以计算出斜齿轮传动的总载荷，并据此进行传动元件的选型和设计。

需要注意的是，在实际工程中，还需要考虑载荷的动态变化、传动系统的寿命和安全系数等因素，以确保传动系统的可靠性和稳定性。

除了上述计算公式外，还有一些特殊情况下的载荷计算方法，比如斜齿轮传动的动载荷、冲击载荷和过载载荷等。

对于这些特殊情况，需要根据具体的工程要求和实际情况进行详细分析和计算。

齿轮承载能力作者：佚名文章来源：网络转载点击数： 3 更新时间：2006-5-2在齿轮传动中﹐齿轮失效前所能传递的最大允许载荷。

齿轮的承载能力取决於齿轮的尺寸﹑结构﹑材质﹑製造水平﹑润滑条件﹑允许的损伤程度﹑要求的寿命和可靠度等。

失效形式齿轮的齿圈﹑轮辐和轮轂等部分通常按经验设计﹐结构尺寸的安全係数较大﹐一般很少遭受破坏。

齿轮的失效主要出现在轮齿上。

轮齿的失效形式主要有轮齿摺断﹑点蚀﹑胶合﹑磨损和塑性变形等(图1 齿轮轮齿的主要失效形式 )。

不过﹐轮齿每一种失效形式的出现并不是孤立的﹐齿面一旦出现了点蚀或胶合﹐就会加剧齿面的磨损﹔齿面的严重磨损又将导致轮齿的摺断等。

轮齿摺断轮齿受载后齿根处的弯曲应力最大﹐当轮齿弯曲应力超过其极限应力时就会发生过载摺断或疲劳摺断。

轮齿摺断一般发生在齿根部分﹐可能一个或多个齿沿齿长整体摺断﹐也可能发生局部摺断。

点蚀在润滑良好的闭式传动中﹐齿面在过高的循环变化的接触应力作用下產生疲劳裂纹﹐裂纹不断扩展蔓延﹐导致工作齿面小块金属剥落﹐形成麻点﹐即点蚀。

点蚀严重时会產生强烈振动和机械噪声﹐使齿轮不能正常工作。

点蚀一般首先出现在节线附近的齿根表面。

胶合在高速重载齿轮传动中﹐油膜会因瞬时高温而破坏﹐相嚙合齿面的金属形成局部熔焊﹐导致较软齿面上的金属撕落﹐形成沟痕。

在低速重载齿轮传动中﹐有时也常因局部压应力很高﹐两接触齿面间油膜被刺破而黏著。

胶合时振动和噪声增大﹐轮齿很快失效。

磨损在闭式传动中﹐润滑油供应不足﹐油不清洁﹐齿面易產生磨损。

在开式传动中﹐灰尘和各种颗粒等进入嚙合齿面会造成磨料磨损。

磨损使齿厚减薄﹑侧隙加大﹐造成衝击﹐降低弯曲强度﹐严重时使轮齿过载摺断。

塑性变形在过大的应力作用下﹐轮齿材料因屈服而產生的塑性流动﹐如齿面碾击塑变﹑鳞皱﹑起脊﹑齿体的歪扭和齿形剧变等。

这些现象多发生在硬度低的齿轮上﹐严重时会破坏正常齿廓﹐使之失去工作能力。

强度计算在机械工程中﹐轮齿的强度计算方法主要有两种。

齿轮弯曲应力计算公式齿轮弯曲应力计算公式弯曲应力概述齿轮在工作时会受到弯曲应力的作用，因此需要对其进行弯曲应力的计算。

弯曲应力是指齿轮在受到外载荷作用时，齿轮齿面上产生的弯曲变形所引起的应力。

弯曲应力计算公式齿轮弯曲应力的计算需要考虑齿轮的几何参数以及受力情况，下面是常用的齿轮弯曲应力计算公式：1.弯曲应力（sigma）的计算公式：sigma = (F * l) / (b * h^2)其中，sigma为弯曲应力，F为外载荷，l为齿轮的长度，b为齿轮的宽度，h为齿轮的模数。

2.弯曲应力（sigma）的修正计算公式：sigma = (F * l) / (b * h^2) * K其中，K为修正系数，由齿轮和齿轮轴的材料性质决定。

3.弯曲应力（sigma）的安全系数计算公式：安全系数 = 弯曲应力极限 / 弯曲应力其中，弯曲应力极限为齿轮材料的弯曲应力极限值。

弯曲应力计算公式举例假设有一台齿轮传动装置，齿轮的模数为2mm，宽度为20mm，长度为100mm。

外载荷为500N，齿轮材料的弯曲应力极限为200MPa。

现在需要计算齿轮的弯曲应力以及安全系数。

1.计算弯曲应力：sigma = (F * l) / (b * h^2)= (500 * 100) / (20 * 2^2)= 125MPa根据计算得到的公式，齿轮的弯曲应力为125MPa。

2.计算安全系数：安全系数 = 弯曲应力极限 / 弯曲应力= 200MPa / 125MPa=通过计算得到的公式，齿轮的安全系数为，表示齿轮的弯曲应力远小于材料的弯曲应力极限，具有较高的安全性。

以上是对齿轮弯曲应力计算公式的列举和举例说明，根据实际情况，可以根据公式进行齿轮的弯曲应力计算，从而评估其结构的合理性和安全性。

当然，还有一些其他的弯曲应力计算公式可以应用于不同的齿轮情况或者特定的应用场景。

这些公式可以根据具体的设计要求和齿轮的几何参数选择使用。

以下是一些常见的齿轮弯曲应力计算公式的补充：1.挤压应力计算公式：当齿轮小于标准公称模数时，可以使用以下公式计算挤压应力：sigma_1 = (F * l * b * h) / (m * p * d * b _s)其中，sigma_1为挤压应力，m为模数，p为压力角，d为齿轮的齿顶直径，b_s为齿宽。

齿轮传动的受力分析齿轮传动是一种常见的机械传动方式，其主要特点在于能够有效地将输入轴的旋转速度转换为输出轴的旋转速度，并将旋转力矩进行传递。

齿轮传动具有传递功率大、传动效率高、运转平稳、使用寿命长等优点，广泛应用于机械制造领域。

齿轮传动的受力分析是研究齿轮传动力学特性的重要内容，这主要涉及到力矩传递、载荷分配、齿面接触等方面的问题。

以下将简要介绍齿轮传动的受力分析过程。

一、齿轮传动的力矩传递在齿轮传动中，力矩是通过齿轮齿面间的接触传递的。

因此，在进行齿轮传动的受力分析时，需要先求出齿轮的齿面接触力，从而确定齿轮传递的力矩。

齿轮齿面间的接触力主要由两部分组成：正向接触力和切向接触力。

正向接触力是指沿着齿轮轴向方向的力，主要用于传递齿轮的轴向载荷；切向接触力是指垂直于齿轮轴向方向的力，主要用于传递齿轮的扭矩。

在齿轮传动的受力分析中，通常采用Hertz接触理论来求解齿轮齿面间的接触力。

Hertz接触理论认为，在齿轮齿面间的接触区域内，应力分布呈现出一个类似于椭圆形的曲面。

根据该曲面的形状和大小，可以计算出齿轮齿面间的接触应力和接触面积。

一般来说，齿轮齿面间的接触应力越大，接触面积越小，齿轮的寿命就越短。

二、齿轮传动的载荷分配在齿轮传动中，不同的齿轮会承受不同的载荷，其原因主要是由于齿轮的尺寸、材料、齿形等不同。

因此，在进行齿轮传动的受力分析时，需要对齿轮的载荷分配进行研究。

齿轮载荷分配的主要方法有两种：按齿数配载法和按力配载法。

按齿数配载法是指根据齿轮的齿数比例来确定齿轮的载荷分配，这种方法简单、实用，但往往不能考虑到齿轮的实际情况。

按力配载法是指根据齿轮的载荷情况来计算其分配比例，这种方法更为精确，但需要进行较复杂的数学计算。

三、齿轮传动的齿面接触齿面接触是齿轮传动中的一个重要问题，直接影响到齿轮的使用寿命和传动效率。

在齿轮传动的受力分析中，需要关注齿面接触区域的形状、大小、位置等因素，并采取相应的措施来避免齿面接触问题的发生。

机械齿轮应力分析报告机械齿轮是一种常用的传动装置，广泛应用于各种机械设备中。

齿轮的应力分析对于确保机械传动的正常运行至关重要。

本报告将对机械齿轮的应力分析进行详细介绍。

一、齿轮的应力分析方法1. 力学分析法力学分析法是通过使用力学原理和公式，对齿轮的受力情况进行分析。

通过计算齿轮的受力情况，可以得到齿轮的应力分布情况。

2. 有限元分析法有限元分析法是通过将齿轮分割为许多小元素，然后对每个小元素进行独立的应力分析，最后将所有小元素的应力结果综合起来，得到齿轮的整体应力分布情况。

二、齿轮的应力分析内容1. 齿轮的接触应力分析齿轮在传动过程中，由于齿轮的啮合，会产生接触应力，该应力对齿轮的强度和寿命有着重要的影响。

因此，需要对齿轮的接触应力进行分析，以确定齿轮的强度。

2. 齿轮的弯曲应力分析齿轮在传动过程中，由于受到转矩的作用，会产生弯曲应力。

该应力对齿轮的变形和破坏有着重要的影响。

因此，需要对齿轮的弯曲应力进行分析，以确定齿轮的变形和强度。

3. 齿轮的疲劳应力分析齿轮在使用过程中，由于反复的加载和卸载作用，会产生疲劳应力。

该应力是齿轮破坏的主要原因之一。

因此，需要对齿轮的疲劳应力进行分析，以确定齿轮的寿命。

三、齿轮应力分析的结果通过对齿轮的应力分析，可以得到如下结果：1. 齿轮的应力分布情况：确定齿轮哪些部位的应力较大，从而采取相应的加强措施。

2. 齿轮的应力大小：确定齿轮的最大应力值，以确保齿轮的强度和寿命。

3. 齿轮的变形情况：确定齿轮在工作过程中是否发生变形，从而调整齿轮的设计参数，以确保其正常运行。

四、齿轮应力分析的意义1. 确保齿轮的强度和寿命，从而提高机械设备的可靠性和安全性。

2. 指导齿轮的设计和制造，从而在设计阶段就预防和解决齿轮应力引起的问题。

3. 对齿轮的使用和维护提供指导，从而延长齿轮的使用寿命。

总之，齿轮的应力分析是确保机械传动正常运行的重要手段之一。

通过对齿轮的应力分析，可以得到齿轮的应力分布情况、应力大小和变形情况，从而指导齿轮的设计和制造，并提高机械设备的可靠性和安全性。

1. 齿轮传动的载荷计算(1) 直齿圆柱齿轮传动的受力分析圆周力：径向力：法向力：o d1——小齿轮的分度圆直径mmoα——分度圆压力角o T1——小齿轮传递的名义转矩(N.m)o P1为小齿轮所传递的功率（KW）o n1为小齿轮转速（rpm）作用在主动轮和从动轮上的力大小相等，方向相反。

主动轮上的圆周力是阻力，其方向与它的回转方向相反；从动轮上的圆周力是驱动力，其方向与它的回转方向相同；两轮所受的径向力分别指向各自的轮心。

齿面上的总法向力方向则为啮合点的法向方向，对于渐开线齿廓即为通过啮合点与基圆相切的啮合线方向。

(2) 斜齿圆柱齿轮传动的受力分析圆周力：径向力：轴向力：法向力：∙αt——端面分度圆压力角；∙αn——法向分度圆压力角；∙β——分度圆螺旋角；∙βt——基圆螺旋角。

(3) 直齿锥齿轮传动的受力分析法向力Fn集中作用在齿宽节线中点处，则Fn可分解为互相垂直的三个分力。

圆周力：径向力：轴向力：dm1——小齿轮齿宽中点分度圆直径mm；δ1——小锥齿轮分度圆锥角圆周力和径向力的方向判别与直齿圆柱齿轮判别方法相同，轴向力方向分别指向各自的大端。

由于锥齿轮传动两轴的空间交角为90°，因此存在以下关系：；。

负号表示方向相反。

(4) 齿轮传动的计算载荷齿轮承受载荷常表现为其传递的力矩或圆周力。

由上述力的分析计算所得出的圆周力为齿轮传动的名义圆周力。

实际工作中，由于各种因素的影响，齿轮实际承受的圆周力要大于名义圆周力。

考虑各种因素的影响，实际圆周力Ftc为：Ftc也称为计算载荷。

1）KA——使用系数。

2）KV——动载系数。

3) KHα和KFα——齿间载荷分配系数。

4) KHβ和KFβ——齿向载荷分布系数。

2. 齿轮传动应力分析齿轮传动工作过程中，相啮合的轮齿受到法向力Fn的作用，主要产生两种应力：齿面接触应力和齿根弯曲应力。

(1) 齿面接触应力σH齿轮传动工作中，渐开线齿面理论上为线接触，考虑齿轮的弹性变形，实际上为很小的面接触。

齿轮弯曲应力齿轮是指由齿轮轴和齿轮齿组成的机械传动元件，同步传递转矩和转速。

在齿轮传动中，齿轮齿的弯曲应力很容易发生，这对齿轮的使用寿命和传动效率有很大的影响。

齿轮弯曲应力的原因主要是由于齿轮的负荷和形状导致载荷方向发生变化。

在齿轮齿的侧面，压力和张力作用于不同的位置，而在齿根和齿槽底上，压力力量的影响最大。

齿轮弯曲应力的大小与齿轮的载荷有关，载荷越大，弯曲应力也越大，这将导致齿轮的强度受到影响。

因此，在设计齿轮时，需要考虑到齿轮的设计、制造和材料的选择，以使其能够承受预期的载荷。

齿轮弯曲应力对齿轮的影响主要表现在以下方面。

1.齿轮变形：齿轮的弯曲应力会导致齿轮的变形，从而影响齿轮的精度和传递效率。

2.齿轮疲劳：齿轮的弯曲应力会增加齿轮的疲劳损坏的风险。

在齿轮的使用过程中，如果应力超过了齿轮材料的极限强度，齿轮将产生疲劳断裂。

3.齿体表面磨损：齿轮的弯曲应力会导致齿轮齿间距离的变化，从而导致齿体表面的磨损加剧，进一步影响齿轮的使用寿命。

为减少齿轮弯曲应力对齿轮的影响，有一些措施可以采取。

1.选用合适的齿轮材料：齿轮材料的强度应与预期负荷相匹配。

不同的应用需要不同的齿轮材料，例如，低载荷应用可以使用低强度的钢铸造齿轮，而高载荷应用则需要使用合金钢等高强度材料制造齿轮。

2.优化齿轮设计：减少齿轮弯曲应力的一种方法是优化齿轮的设计。

通过改变齿轮的几何形状、齿数和齿轮的结构，可以降低弯曲应力，延长齿轮的使用寿命。

3.适当的齿轮预载荷：有效的预载荷可以减少齿轮的弯曲应力，提高齿轮的传动效率和精度。

总之，齿轮弯曲应力是影响齿轮传动效率和使用寿命的重要因素。

对于齿轮的设计、制造和使用，需要综合考虑材料、载荷以及齿轮结构等因素，以减少应力弯曲的影响，提高齿轮的工作效率和寿命。