当前位置：文档之家 › 运筹学课件 第五节 灵敏度分析

运筹学课件 第五节 灵敏度分析

  • 格式：ppt
  • 大小：421.00 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

运筹学课件 灵敏度分析与参数规划

运筹学课件 灵敏度分析与参数规划
2013-4-7 灵敏度分析与参数规划 5-7
灵敏度分析的任务
线性规划的灵敏度分析要解决两个问题：
一个或几个系数或要素变化后，当前的
最优解或最优基是否有变。
这些系数在什么范围内变动时，当前的
最优解或最优基不变。 另外，一旦当前解受影响就要运用适当 方法对其进行调整，以便得到新的最优解。
2013-4-7 灵敏度分析与参数规划 5-8
分析结果的处理方法
针对上述五种不同的分析结果，可按下列相 应的调整方法进行处理。 分析结果 处理方法
最优解不变
最优基不变 变为可行解 变为正则解 变为普通解
2013-4-7 灵敏度分析与参数规划
计算 CN - CBB-1N
计算 XB(*) = B-1b 原始解法求最优解 对偶解法求最优解 混合解法求最优解
2013-4-7 灵敏度分析与参数规划 5-3
生产计划问题
cj CB XB
0 0 0 -1 0 0 3 -1 2 0 3 -1 2 0 3 -1
b
2 3 x1 x2
0 x3
0 x4
0 x5
0 0 1 0 -1/2 0 1/4 -3/4 -1/2 [2] 1/4 1/4 0 1 0 0
θ
x3 8 x4 16 x5 12 z 0 x3 2 x4 16 x2 3 z -9 x1 2 x4 8 x2 3 z -13 x1 4 x5 4 x2 2 z -14
5-14
2013-4-7
灵敏度分析与参数规划
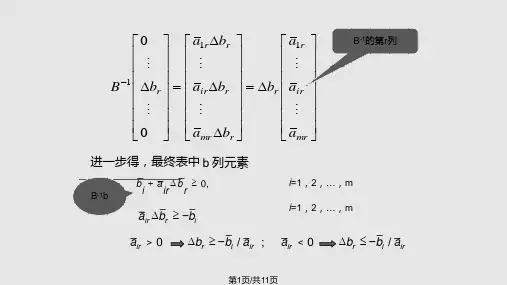
2. 基变量系数 cr 的变化分析
当基变量 xr 的系数 cr (CB)变化 cr 时，就会引起 CB 的变化，从而影响到各非基变量 xj 对应的j 。 设 CB=( 0, …, cr , …,0 )，若要求原最优解不变，则 新的检验数必须满足 j' = cj - (CB +CB )B-1Pj = cj - CBB-1Pj - CB B-1Pj =j - [(0, …,cr , …,0)(b1j, …, brj, …, bmj)T] =j - cr brj ≤0 于是得到 cr ≤j／brj , brj < 0 j=1 , 2 , …, n cr ≥j／brj , brj > 0 cr的变化范围为是 max { j /brj | brj > 0 }≤ cr ≤ min { j /brj | brj < 0 }

运筹学图解法的灵敏度分析 PPT课件

运筹学图解法的灵敏度分析 PPT课件
交于该顶点的两条直线的斜率即cj变动范围，cj在两 条直线斜率之间变动时，原线性规划问题的最优解
不变，最优值变动（cj变动）。
11
四、约束条件中右边系数bi的 灵敏度分析
例：
max F 6 x 1 4 x 2 s .t . 2 x 1 3 x 2 10 4 x 1 2 x 2 12 x1, x2 0
18
图解法
400
2x1x2 400
可行解域为OABCD 最优解为B点（50，250）
300
A
B
x2 250
200
C
100
x1x2 300
最优生产方案为： 甲生产50，乙生产250；
此时， 总利润为27500元。
D
O
100
200
300
400
5x0110x200
19
现提高设备可利用台时数
（b1=300
12
讨论：当b1=10 b1=11时对 原问题的影响
x2
5
4x12x212
A 3
B
1
2x13x210
O
C
2
4
6
x1
6x14x20 6x14x220
13
讨论：b1变动对原问题的影响 （b1=10 b1=11）
x2
5
4x12x2 12
A’
A3
B’
B
2x13x2 11
1
2x13x210
O
C
2
4
6
x1
6x14x20
100
设备台时的约束条件
为0
D D’
O
100
200
300
400

运筹学灵敏度分析

运筹学灵敏度分析

只需由 j 0解得c j的范围。
(2) c j 是基变量x j的价格系数 这时要影响所有的检验 数
i ci (c1 ci ci cm ) B Pi , 应由所有的 i 0解得公共的c j。
1
p11-2
例1：在（煤电油例）中，其单纯形终表如下：
0 x 7 x 12 x
3 1
运筹学
2

84 20 24
0 1 0
0
0 0 1
0
1 0 0
0
- 0.32 0.4 - 0.12
- 1.36
1.16 - 0.2 0.16
- 0.52
z 428
（1）甲产品的价格在何范围内变化时，现最优解不变？
解：甲产品的价格c1是基变量的价格系数。 0.32 由 4 0 0 7 c1 12 0.4 2.8 0.4c1 1.44 0 0.12 得 c 3.4， 1.16 由 5 0 0 7 c1 12 - 0.2 1.4 0.2c1 1.92 0 0.16 得 c 2.6，
2
运筹学
例1：在（煤电油例）中，其单纯形终表如下：
0 x 7 x 12 x
3
1
2

84 20 24
0 1
0
0 0 1
1 0
0
- 3.12 1.16 0.4 - 0.2
- 0.12 0.16
z 428
0
0
0
- 1.36
- 0.52
（3）若有人愿以每度1元的价格向该厂供应25度电，是 否值得接受？
§3.4 灵敏度分析
灵敏度分析——研究系数变化对最优解的影响.

(方案)第三章 第五节 灵敏度分析.ppt

(方案)第三章 第五节 灵敏度分析.ppt

..........
28
8.1 参数c的变化
例1 试分析以下参数线性规划问题当参数 t≥0时的最优解变化。
..........
8
举例
例5.2:
Max z = 2x1 + 3x2 + 0x3 + 0x4+ 0x5
s.t. x1 + 2x2 + x3 = 8 4x1 + x4 = 16 4x2 + x5 = 12 x1 , x2 , x3 , x4 , x5 ≥ 0
..........
9
下表为最优单纯形表,考虑
解 设家电2的利润为(1+λ)元，反映到最终的单纯形表中如 下：
cj→
2 1+λ 0
0
0
CB
XB
b
x1
x2
x3
x4
x5
0
x3 15/2 0
0
1
5/4
-15/2
2
x1 7/2 1
0
0
1/4
-1/2
1+λ x2 3/2 0
1
0
-1/4
3/2
cj-zj
0 0 0 -1/4+λ/4 -1/2-3λ/2
..........
11
为使表中的解仍为最优，应有
1 1 0, 1 3 0
44
22
解得 1 1
3
即家电2的利润变化范围应满足
2 3
c2
2
..........
12
5.2 资源数量(右端常数br)变化的分析
资 源 数 量 变 化 是 指 资 源 中 某 系 数 br 发 生 变 化 ， 即 b使r′最=终br表+Δ中b原r。问并题假的设解规相划应问地题变的化其为他系数都不变。这样 XB′=B-1(b+Δb) 这里Δb=(0,…，Δbr,0,…，0)T。只要XB′≥0，因最终 表中检验数不变，故最优基不变，但最优解的值发生了变 化，所以XB′为新的最优解。新的最优解的值可允许变化 范围用以下方法确定。

系统工程概论运筹学6.5灵敏度分析.ppt

系统工程概论运筹学6.5灵敏度分析.ppt

❖ 原问题最优解不变，若反之
j
0
❖ 则以 B1Pj 替代原最优表的第j列，用单纯 形法继续求解至最优解。
❖ （4）改变某基变量系数列向量的分析
❖ 设 x j 基变量的系数列向量变为
Pj
，试分
析原最优解的变化。
❖
Pj
的变化将导致B的变化，因而原最优表
❖ 所有元素都将发生变化，似乎只能重新计算
❖ 但是经过认真分析，还是可以利用原最优解 来计算新的最优解。
-2/5 1/5
-2 X1 11/5 1
σj
0
0 7/5
-1/5 -2/5
0 -9/5+Δc3 -8/5 -1/5
只要-9/5+Δc3 ≤0 ，即Δc3 ≤9/5 则原最优解不变
表中σ3= c3+Δc3-(c2×a13+c1×a23 ) = -9/5+Δc3
❖ 2)设基变量 XB 的价值系数 CB 有增量 CBr ，
备注
CB X B B 1b x1 x2 x3 x4
4 x2 70 0 1 1/2 -1/4
K=1
6 x1 -5 1 0 -1/4 3/8
L=2
j 4 x2 60 0 x3 20
j
0 0 -1 /2 -5/4
2 1 0 1/ 2 4 0 1 3/2
2 0 0 2
新的最优 解为：
x2
x3
6 2
00,
例4
例2增加3x1+ 2x2≤15，原最优解不 满足这个约束。于是
Ci
2
3
000
0
CB XB b
X1
X2
X3 X4 X5
X6
2 X1 4

运筹学05-灵敏度分析

运筹学05-灵敏度分析

0 1 0
4 4 2
2 1
2
4 1
2 1
8
1 0
4 0 0
4 4 2
0 -8 2
40 4-8 22
4 -4 4
将b’代入原最优单纯形表中，运用对偶单纯形法计算最优解。
Ci
2
3
0
0
0
B-1b
CB
XB
x1
x2
x3
x4
x5
2
x1
1
0
0
1/4
0
4
0
(1)、参数A，b，C在什么范围内变动，对当前方案无影响？
(2)、参数A，b，C中的一个(几个)变动，对当前方案影响？
(3)、如果最优方案改变，如何用简便方法求新方案？
当线性规划问题中的一个或几个参数变化时，可以用单纯 形法从头计算，看最优解有无变化，但这样做既麻烦又没 有必要。
灵敏度分析一词的含义是指对系统或事物因周围条件变化 显示出来的敏感程度的分析。
5.1 目标函数系数的灵敏度分析
考虑检验数 σ C CB B1 A
σ j C j CB B1 Pj
(1) 若ck是非基变量的系数：
设 c'k ck Δck ,则 σ'k ck Δck CB B1 Pk σk Δck 当 σ'k σk Δck 0 即 σk Δck 时 原最优解不变；
B-1(b + b) ≥ 0 ， 则最优基不变，即基变量保持，只有值的变化； 否则，需要利用对偶单纯形法继续计算。
例 Max z 2x1 3x2
x1 2x2 8
s.t
4x1 16 4x2 12
x1,x2 0
解: 下表为最优单纯形表

运筹学-线性规划灵敏度分析_图文

运筹学-线性规划灵敏度分析_图文
在目前计算机普及率很高的情况下，通常的方法是程序 中修改A后重新计算成即可。
例2.1 在例1.1中新增一种产品:防盗门
例2.2 在例1.1中新增一个约束：电力限制
作业:P50—52,1,3,5
运筹学 小结： 一般信息的变化： 价值向量—市场变化 右端向量—资源变化 系数矩阵—技术进步
线性规划
C的变化只影响检验数（对偶问题的解），不影响原问题 的基本解；
格，所以它们所需要的主要原料（木材和玻璃）、制作时间、最大销售量与利润均 不相同。该厂每天可提供的木材、玻璃和工人劳动时间分别为600单位、1000单位 与400小时，详细的数据资料见下表。问： （1）应如何安排这四种家具的日产量，使得该厂的日利润最大？ （2）家具厂是否愿意出10元的加班费，让某工人加班1小时？ （3）如果可提供的工人劳动时间变为398小时，该厂的日利润有何变化？ （4）该厂应优先考虑购买何种资源？ （5）若因市场变化，第一种家具的单位利润从60元下降到55元，问该厂的生产计 划及日利润将如何变化？
表1 雅致家具厂基本数据
家具类型 1
劳动时间 （小时/件）
2
木 材（单 位/件）
4
玻 璃（ 单位/件）
6
单位产品利 润（元/件）
60
最大销售量 （件）
100
2
1
2
2
20
200
3
3
1
1ห้องสมุดไป่ตู้
40
50
4
2
2
2
30
100
可提供量
400小时
600单位
1000单位
解：依题意，设置四种家具的日产量分别为决策变量 x1,x2,x3,x4,目标要求是日利润最大化，约束条件为三 种资源的供应量限制和产品销售量限制。

灵敏度分析(运筹学).ppt

灵敏度分析(运筹学).ppt

0
0
1
0
0
0
x3
1 0
0 1 1
0 2 -1
-1
0
x4
0 1
0
0
-3/2 -1 1
-1
2.5.1 单纯形法的矩阵描述
1. 约束方程系数矩阵的变化
约束方程系数矩阵
，进行初等行
变换，相当于左乘一个相应的初等阵。
即
，在A中所包含的矩阵B，左
乘 后，则得到
。
2. 约束方程右端项的变化
3. 目标函数系数的变化
1. 灵敏度分析的概念：
当某一个参数发生变化后，引起最优解如何改变的 分析。 可以改变的参数有： bi——约束右端项的变化，通常称资源的改变； cj ——目标函数系数的变化，通常称市场条件的变 化； pj ——约束条件系数的变化，通常称工艺系数的变 化； 其他的变化有：增加一种新产品、增加一道新的工 序等。
2．分析原理及步骤：
（1）借助最终单纯形表将变化后的结果按下述基
本原则反映到最终表里去。
B①-1bi△变b化：=
（b+△b）´=B-1 b´+B-1 △b
（b+△b）=
B-1
b+
②pj变化：（pj+△ pj ）´= B-1 （pj+△ pj ）= B-1 pj+ B-1 △ pj = pj ´+ B-1 △ pj
围来确定最优解是否改变。 由于系数的改变，最优值z可能发生 变化而不再是原值了。
2、约束条件右端值的变化
约束条件右端值每增加一个单位 引起的最优值的改进量称为对偶 价格。
对偶价格只适用于在右端值仅发 生了很小变动的情况
2.5.3 单纯形法灵敏度分析

运筹学课件灵敏度分析

运筹学课件灵敏度分析

运筹学教程
Cj
210
CB 基 b X1 x2 x3
0 x3 15 0
51
2 x1 5 1
10
0 x4 2 0
-4 0
Cj-Zj
0
-1 0
00 x4 x5 00 01 1 -6 0 -2
工厂的最优生产计划改为只生产产品1，每天 的生产数量5件。
解：（2）
设每天的调试可用能力为5
运筹学教程
1 b' B1b 0
x5
x4
5
24
x1, x2 , x3, x4 , x5 0
用单纯形法求解如下：
运筹学教程
Cj
210 0 0
CB 基 b X1 x2 x3 x4
x5
0 x3 15/2 0 2 x1 7/2 1 1 x2 3/2 0
01 00 10
5/4 -15/2 ¼ -1/2 -1/4 3/2
Cj-Zj
0
8
2
3 / 2 0 2
运筹学教程
将其反映到最终的单纯形表，原问题非可行解， 采用dual单纯形法
Cj
2
CB 基 b X1
0 x3 35/2 0
2 x1 11/2 1
1 x2 -1/2 0
Cj-Zj
0
10 x2 x3 01 00 10 00
00 x4 x5 5/4 -15/2 ¼ -1/2 [-1/4] 3/2 -1/4 -1/2
aij
y i
i 1
运筹学教程
（2）、检查原问题是否仍为可行解。 （3）、检查对偶问题是否仍为可行解。
原问题
可行解 可行解 非可行解 非可行解
对偶问题
可行解 非可行解 可行解 非可行解

运筹学灵敏度分析PPT课件

运筹学灵敏度分析PPT课件
0 a1r br
a1r
B 1
br
air br
br
air
0 amr br
amr
B-1的第r列
进一步得，最终表中 b 列元素
B-1b
bi + a ir br 0,
air br bi
i=1，2，…，m i=1，2，…，m
air > 0
br bi / air ; air < 0
0 4 0.25 0
B1b
+
B1
b2
4
+
0.5
b2 0
0 2 0.125 0
可得 △b2≥-4/0.25=-16, △b2≥-4/0.5=-8, △b2≤2/0.125=16 由公式知△b2变化范围[-8,16], 显然b2变化范围[8,32]
例题: 将上面例题进行实际应用。每台设备台时的影子价格为1.5元。若该 厂又从别处抽出4台时用于生产两种产品，求这时该厂生产两种产品的最优方 案。
生产规模条件下单位产品利润或单价的可变范围。 2、代表单位原料单价时，灵敏度分析用于预先确定保持现有配方条件下，原
料单价的可变动范围。
第10页/共11页
感谢您的观看！
第11页/共11页
解：这时最终计算表为
第7页/共11页
cj
2 3 + △c2 0
0
0
CB XB b x1
x2
x3
x4
x5
2 x1 4 1 0
0 0.25 0
0 x5 4 0 0
-2 0.5
1
3 x2 2 0 1 0.5 –0.125 0
cj-zj
0 △c2 -1.5 -0.125 0

管理运筹学 第五章灵敏度分析

管理运筹学 第五章灵敏度分析
3
c8 z8 c8 qi ai 8 9 (5 0 4 0.25 3 1)
i 1
50
结论：生产x8有利。
8
第五章 线性规划问题的灵敏度分析
§5.2 对cj 值的灵敏度分析
概述
•cj 变动可能由于市场价格的波动，或生产成本的 变动 •cj 的灵敏度分析是在保证最优解的基变量不变 的情况下，分析cj 允许的变动范围cj •cj 的变化会引起检验数的变化，有两种情况 –非基变量对应的价值系数变化，不影响其 它检验数 –基变量对应的价值系数变化，影响所有非 基变量检验数
概 述
• b的灵敏度分析就是研究最优解基变量保 持不变但基变量的取值可以变化的条件 下b的取值范围 • 设 XB=B1b 是最优解，则有XB=B1b0 • b 的变化不会影响检验数 • b 的变化量 b 可能导致原最优解变为非 可行解（不满足非负约束）
16
右端项 bi 的灵敏度分析
• 在将“≤”形式的约束条件变为“=”形式时，对第i行 的约束条件方程左端要加一个松弛变量Xn+i，因此， 最优解表中B-1可表示为
25
1、对应基变量的 aij ，且资源bi已全部用完 aij=0 2、对应基变量的 aij ，但资源bi未用完
xn i < aij xj
26
3、对应非基变量的 aij
设 x j为非基变量, 则有 : z 0 a kj qk j
k 1 m
设a ij变动a ij , 则有 : z z a ij qi
二、边际值的求解
以(max,)型为例：
z o 最大利润的增量 前面讨论过 qi =(CBb-1)i bi 第i种资源的增量
Zn+i=CBb-1Pn+i =(CBb-1)i

运筹学线性规划对偶理论与灵敏度分析ppt课件

运筹学线性规划对偶理论与灵敏度分析ppt课件
2020/2/21
2020/2/21
一、单纯形法计算的矩阵描述
本节以对称形式的原始-对偶问题为讨论的基础， 除非特别需要，一般不再专门说明。
P. max z = CX AX≤b
D. min w = Yb YA≥C
X≥0
Y≥0
原问题通过加入松弛变量 Xs 可以化为标准形式：
max z = CX +0Xs st. AX + IXs = b
max z = x1－2 x4 + x5 － x6
x1 － x4 － x5 + x6 ≤ 2 x1－ x4 － x5 + x6 ≤ - 1 x1 + x4 + x5 － x6 ≤ 1 2x1+ x4 － x5 + x6 ≤- 2 x1 , x4 , x5 , x6 ≥0
（2）写出上述 对称形式线性规 划问题的对偶。
a12y1+ a22y2 + … + am2ym ≥ c2 ……
a1ny1+ a2ny2 + … + amnym ≥ cn y1 , y2 , …, ym ≥0
2020/2/21
原问题：
max z = C X AX ≤ b X ≥0
Y=(y1,y2,…,ym) 对偶问题： min w = Y b YA≥C Y≥0
max z =c1x1+ c2x2 +… + cnxn
a11x1+ a12x2 + … + a1nxn ≤ b1
st.
a21x1+ a22x2 + … + a2nxn ≤ b2 ……
am1x1+ am2x2 + … + amnxn ≤ bm

运筹学讲义-灵敏度分析

运筹学讲义-灵敏度分析
k=1 −1 m
qi = ∂f ( x) ∂bi− = (CBB−1)i , 左导数 机会成本 zn+i = CBB−1P +i = (CBB−1)i n zn+i 因此 qi = − zn+i
−1 m
, 松弛变量 人工变量 剩余变量
m
机会成本的另外表达形 式 z j = CBB Pj = ∑(CBB )i aij = ∑qiaij
16
2.4.7 灵敏度分析举例 例2.4.3 某工厂生产三种产品 A, B, C，有五种生产组合方案。 ，有五种生产组合方案。
下两表给出有关数据。 产品至少110 个，求收 下两表给出有关数据。规定每天供应 A产品至少 产品至少 益最大的生产方案。 益最大的生产方案。
17
例2.4.3
为已选定各种组合方案的组数(j=1,2,…,5)， x6为A产品 解：设xj为已选定各种组合方案的组数 ， 产品 的剩余变量， 分别为工人工时和机器工时的松弛变量。 的剩余变量， x7，x8分别为工人工时和机器工时的松弛变量。
©管理与人文学院
1999，4 ，
忻展红
2.4 灵敏度分析
灵敏度分析又称为后优化分析
2.4 线性规划的灵敏度分析
• 线性规划是静态模型 • 参数发生变化，原问题的最优解还是不是最优 参数发生变化， • 哪些参数容易发生变化 – C, b, A • 每个参数发生多大的变化不会破坏最优解 • 灵敏度越小，解的稳定性越好 灵敏度越小，
18
例2.4.3 • • • • • • • • • 最优解的B 最优解的 –1是什么 产品A的影子价为多少 产品 的影子价为多少 组方案的生产费用提高2元 第II组方案的生产费用提高 元，是否要调整生产组别 组方案的生产费用提高 若工人加班费为1元 小时 小时， 若工人加班费为 元/小时，是否要采取加班措施 若通过租借机器增加工时， 若通过租借机器增加工时，租费的上限应为多少 A产品的订购合同是否有利 产品的订购合同是否有利 若要选用第IV组方案，该组的生产费用应降低多少 若要选用第 组方案， 组方案 若工人加班费为0.3元 小时 小时， 若工人加班费为 元/小时，最多允许加班时间多少 若机器租费低于44元 小时 问租几部机器才合适(每天 小时， 若机器租费低于 元/小时，问租几部机器才合适 每天 8小时计 小时计) 小时计 • 若第 组方案使机器工时减少 小时，能否被选入 若第III组方案使机器工时减少 小时， 组方案使机器工时减少0.5小时

运筹学 灵敏度分析

运筹学 灵敏度分析
′ （2）由于 1 是基变量，所以 ξ B = 0, ）由于x 是基变量，
T ′ ξ N = ξ N + (c1′ − c1 )( B −1 N )(1) ( B −1 N 中第1行元素）
1 5 7 1 1 1 ‘ = （ ， ， ）+ ( 1 − 5)(− , , − ) c 6 6 6 6 6 6 ‘ ‘ ‘ c1 c1 c1 ‘ = (1 − , , 2 − ) ≥ 0 ⇒ 0 ≤ c1 ≤ 6 6 6 6
原最优单纯形表
基 XB XB I XN 解
ξ
ξB = 0
B N
T T T ξ N = CB B−1 N − CN ≤ 0
−1
B b T −1 CB B b
−ck )加到检验
数行， 得到新问题的单纯形表. 数行，再令 ξ k′ = 0 ，得到新问题的单纯形表
§6 灵敏度分析
概况
• 信息的不确定性
信息的变化： 信息的变化： 价值向量C—市场变化 价值向量 市场变化 右端向量b—资源变化 右端向量 资源变化 系数矩阵A—技术进步 系数矩阵 技术进步
• 产生的问题
当这些参数变化时，问题的最优解会有什么变化？ 当这些参数变化时，问题的最优解会有什么变化？ 这些参数在多大范围内变化时，最优解不变？ 这些参数在多大范围内变化时，最优解不变？
x4
-1/4 ½ -1/4 -1/4 ½ -1/4 -5/4 1 0 7/4 5/2 7/4 7/4 5/2 7/4 -13/4 5 3
-5/4 ½ -1/4 1 ½ -1/4 0 1 0
x2 x3
Z
x2 x3
Z
x1 x3
最优解 x*=（5, 0, 3） 最优值 z*=-13/4

运筹学单纯形法的灵敏度分析课件

运筹学单纯形法的灵敏度分析课件
• 基变量的cj发生变化，由于影响到cB，从而所有非基变 量的检验数均受到影响（基变量的检验数仍保持为0）。
• 如上例中x1、x2为基变量，则甲、乙产品单位利润变化，将影 响除甲、乙外其他变量的检验数。
运筹学单纯形法的灵敏度分析
6
（一）非基变量目标函数系数的改变
• 上例中，x1、x2为基变量，x3为非基变量，它的最优解为x3=0， 既不安排生产。为什么不生产丙产品呢？因为x3所对应的检 验数Cj-Zj不是绝对值最大者，无法调入成为基变量。
最优 ZC B 值 b运筹2 学单纯3 形法 的1 2 灵敏 度 分析8 最优 Z8值 20
分析
• 从以上计算结果表明，增加一个单位b1（劳动力数量）会使总利 润增加，但在实际经济工作中，b1增加不可能是无限的，因为劳 动力增加太多，而其他条件不变时，势必造成劳动力过剩，影响 生产率，进而影响利润率，即Cj会变化，因此，b1的变化也是有 范围的。
运筹学单纯形法的灵敏度分析
8
• 所以，丙产品单位利润的变动范围是c3<4；
• 讨论： • 假设此时c3增加到6元，产量应为多少？
运筹学单纯形法的灵敏度分析
9
C3已超出变动范围
• 代入单纯形表 最后一段 继续计算。
段
Cj ↓
→ 基
0 b
23 x1 x2
6 x3
0 0 Qi x4 x5
2
x1
1
1
0 （-1） 4 -1
但变量值发生变动（产量变化），最优值也会变动
（总利润变化），即运筹学单纯形法的灵敏度分析
23
x1 4 b1 3 x 2 b1 3 x3 0
Z 2 x1 3 x2
2 4 b1 3 3 b1 3

运筹学课件 第五节 灵敏度分析

运筹学课件 第五节 灵敏度分析
参数 aij,bi,cj 的变化引起的单纯形表上的有关 数字的变化：
b ' B 1b Pj B 1 Pj
' m
(c j z j ) c j aij yi
' i 1
运筹学教程
（2）、检查原问题是否仍为可行解。
（3）、检查对偶问题是否仍为可行解。
原问题
可行解 可行解 非可行解 非可行解
0 0 x3 x4 4/5 1 -1/5 0 1/5 0 -1/10 0
0 x5 -6 1 0 -3/2
随利润的变化，调整如下：
生产产品1为2件，产品2为3件。
运筹学教程
解（2）设产品2的利润1+
Cj
CB 基 b 0 x3 15/2 2 x1 7/2 1+ x2 3/2 Cj-Zj
2 X1 0 1 0 0
运筹学教程
CB 0 2 3
2 x1 基 b x5 3/8 0 x1 11/4 1 x2’ 15/8 0 Cj-Zj 0
Cj

3 x2’ 0 0 1 0
0 0 0 x3 x4 x5 -1/24 -1/6 1 -1/12 1/6 0 1/8 0 0 -5/24 -1/3 0
-M x6 1/24 1/12 -1/8 -M+5/24
将其反映到单纯形表
Cj CB 基 b 0 x3 15/2 2 x1 7/2 1 x2 3/2 Cj-Zj Cj 基 b x3 -9 2 x1 x2’ 3 Cj-Zj
2 X1 0 1 0 0 2 X1 0 1 0 0
1 x2 0 0 1 0 1 x2 0 0 1 0
3 0 X2’ x3 11/2 1 ½ 0 ½ 0 3/2 0 3 x2’ 0 0 1 0 0 x3 1 0 0 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

新的最优生产计划为每天生产1产品：7/2件 生产2产品：0件；生产3产品：3/4件。
运筹学教程
4、分析参数 aij的变化
参数 aij的变化导致系数阵A的元素发生变化。相当于增 加1个新变量（系数阵A增加1列），如果 xj在最终单纯 形表中为基变量，则aij 的变化会使相应的B ,B-1 发生变 化，有可能出现原问题与对偶问题无可行解的情况。引
Hale Waihona Puke 运筹学教程2、分析bi（右端常数）变化：
当bi发生变化时，将影响所有基变量的取值。 1 因为： X B B b 若bi的变化→
①保持B-1b≥0,当前的基仍为最优基，最优解的结构 不变（取值改变）； ②（B-1b）<0,当前基为非可行基,但是仍保持为对偶 可行基, 可用对偶单纯形法求出新的最优解；
运筹学教程
例1-1:(1)如果产品1的利润降至1.5元/件，产品2的利润增加 至2元/件，工厂的最优生产计划？
（2）如果产品1的利润不变，则产品２的利润在什么范围内变 化，工厂的最优生产计划不变？ 解（1）将产品1，2的利润变化直接反映到单纯形表
Cj CB 基 b 0 x3 15/2 1.5 x1 7/2 2 x2 3/2 Cj-Zj
1 ' 1 P6 B P6 0 0
运筹学教程
Cj CB 0 2 1 基 b x3 15/2 x1 7/2 x2 3/2 Cj-Zj
2 X1 0 1 0 0
1 x2 0 0 1 0
0 x3 1 0 0 0
0 x4 5/4 ¼ -1/4 -1/4
0 3 x5 x6 -15/2 -7 -1/2 0 3/2 2 -1/2 1
1.5 2 X1 x2 0 0 1 0 0 1 0 0
0 x3 1 0 0 0
0
0
x4 x5 [5/4] -15/2 ¼ -1/2 -1/4 3/2 1/8 -9/4
运筹学教程
Cj CB 基 b 0 x4 6 1.5 x1 2 2 x2 3 Cj-Zj
1.5 2 X1 x2 0 0 1 0 0 1 0 0
进人工变量，使用单纯形法计算。
如果该厂生产的产品2，生产一件所需要设备A,B
以及调试工序的时间分别变为8h,4h,1h，该产品的 利润变为3元/件，对该公司的最优生产计划有何改 变？
运筹学教程
解：将改变的产品看作是一件新的产品，生产量X2’
8 8 ' 4 , 2 3 ( 0 ,1 / 4 ,1 / 2 ) 4 3 / 2 1 1 1 0 0 5 4 1 4 1 4 15 2 8 11 / 2 1 4 1/ 2 2 3 1 1 / 2 2
-M x6 1/24 1/12 -1/8 -M+5/24
最优生产计划每天生产1产品11/4件；
新产品15/8件。
运筹学教程
5、 增加1个约束条件： 相当于系数阵A增加1行 首先将原最优解代入新增约束检查是否 满足？是，则说明新增约束不影响最优 解。否则再作下面的讨论：
运筹学教程
仍然来看例1-1： （1）如果设备A和调试工序的每天的能力不变，设备B每 天的能力增加到32h，分析公司最优的生产计划的变化； （2）如果设备A和设备B每天的能力不变，则调试工序在 什么范围内变化，问题的最优基不变。
解：（ 1） 0 b 8 0 1 ' 1 b B b 0 0 5/4 1/ 4 1/ 4 15 / 2 0 10 1/ 2 8 2 3 / 2 0 2
C 2 3, P
'
' 2
P2 B P
''
1
' 2
将其反映到单纯形表
Cj CB 基 b 0 x3 15/2 2 x1 7/2 1 x2 3/2 Cj-Zj Cj 基 b x3 -9 2 x1 x2’ 3 Cj-Zj
2 X1 0 1 0 0 2 X1 0 1 0 0
1 x2 0 0 1 0 1 x2 0 0 1 0

N
CN CBB
1
N
例：c4发生变化时， 4 0 ，最优解不变 否则 4 >0,可使用原单纯形法继续迭代求出新 的最优解。
运筹学教程
（2）当cj是基变量的价值系数——它的变化 将影响所有非基变量的检验数.

N
CN CBB
1
N
当cj变化时，如能保持 N 0 ，则当前解仍为 最优解，否则可用单纯形法继续迭代求出新 的最优解。
2 X1 0 1 0 0
1 + 0 x2 x3 0 1 0 0 1 0 0 0
0
0
x4 x5 5/4 -15/2 ¼ -1/2 -1/4 3/2 -1/4+ /4 -1/2-3 /2
运筹学教程

1 4


4
0,
1 2

3 2
0

1 3
1
所以产品利润的变化 范围应满足： 2 3 c2 2
回答两个问题：
运筹学教程
①这些系数在什么范围内发生变化时，最优 基不变（即最优解或最优解结构不变）？ ②系数变化超出上述范围时，如何用最简便 的方法求出新的最优解？ 二、 进行灵敏度分析的基本原则
1、在最优单纯形表的基础上进行；
2、尽量减少附加计算工作量；
运筹学教程
3、灵敏度分析的步骤：
（1）将参数的改变通过计算反映到单纯形表。
参数aij,bi,cj 的变化引起的单纯形表上的有关 数字的变化：
b B b
' 1
Pj B Pj (c j z j ) c j
'
'
1
a
i 1
m
ij
yi
运筹学教程
（2）、检查原问题是否仍为可行解。
（3）、检查对偶问题是否仍为可行解。
原问题
可行解 可行解 非可行解 非可行解
b 列数字为
当b≥0问题的最优基不变，
解得： 1 1
所以调试能力在4~6h
运筹学教程
3、增加一个变量xj的分析
分析步骤： 1、计算 2、计算 3、如果 如果
' j

P
' j
c
j
j
z
1
j
c
j


m
a ij y i
i 1
'
B
Pj

' j
0 , 最优解不变；
0 , 继续计算。
原问题与对偶问题均为非可行解，先使原问题转化为可行解 第一行的约束：x3+4x4-24x5=-9,乘以（-1），加上人工变 量 -x3-4x4+24x5 +x6 =9
Cj CB -M 2 3 基 b x6 9 x1 2 x2’ 3 Cj-Zj
2 X1 0 1 0 0
1 x2 0 0 1 0
3 0 x 2’ x 3 0 -1 0 0 1 0 0 -M
运筹学教程
第五节 灵敏度分析
一、灵敏度分析的含义和内容
1、灵敏度分析：对系统或事物因周围条 件变化显示出来的敏感程度。 研究线性规划模型某些参数或限制量的 变化对最优解的影响称为灵敏度分析。
运筹学教程
2、灵敏度分析的内容： 目标函数的系数变化对最优解的影响； 约束方程右端系数变化对最优解的影响； 约束方程组系数阵变化对最优解的影响 ；
用单纯形法求解如下：
运筹学教程
CB 0 2 1
Cj 基 b x3 15/2 x1 7/2 x2 3/2 Cj-Zj
2 X1 0 1 0 0
1 x2 0 0 1 0
0 x3 1 0 0 0
0 x4 5/4 ¼ -1/4 -1/4
0 x5 -15/2 -1/2 3/2 -1/2
运筹学教程
1、价值系数Cj变化 （1）当cj是非基变量的价值系数——它的变 化只影响 j 一个检验数。
1 ' 1 b B b 0 0 反映到单纯形表， 15 15 2 2 7 1 b 2 2 3 3 2 2
5/4 1/ 4 1/ 4
15 / 2 0 15 / 2 1/ 2 0 /2 3 / 2 3 / 2
对偶问题
可行解 非可行解 可行解 非可行解
结论或继续计算的步骤
问题最优解或最优基不变 单纯形求解最优解 对偶单纯形求解最优解 引进人工变量，新单纯形 表重新计算
运筹学教程
三、 灵敏度分析举例： 例1-1
max Z 2 x1 x 2 5 x 2 15 6 x1 2 x 2 24 s .t . x1 x 2 5 x1 , x 2 0
0 0 x3 x4 4/5 1 -1/5 0 1/5 0 -1/10 0
0 x5 -6 1 0 -3/2
随利润的变化，调整如下：
生产产品1为2件，产品2为3件。
运筹学教程
解（2）设产品2的利润1+ 直接反映到单纯形表
Cj
CB 基 b 0 x3 15/2 2 x1 7/2 1+ x2 3/2 Cj-Zj
CB 0 2 1
运筹学教程
CB 0 2 0
Cj 基 b x3 15 x1 5 x4 2 Cj-Zj
2 X1 0 1 0 0
1 x2 5 1 -4 -1
0 x3 1 0 0 0
0 x4 0 0 1 0
0 x5 0 1 -6 -2