当前位置：文档之家 › 运筹学灵敏度分析题

运筹学灵敏度分析题

  • 格式：doc
  • 大小：264.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

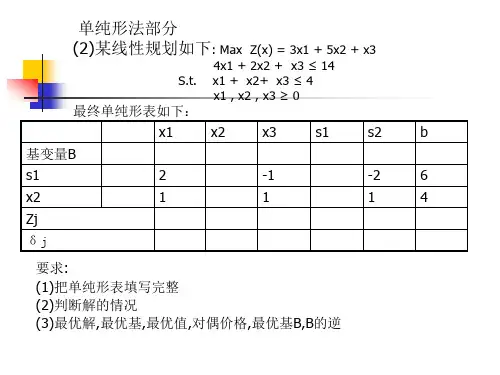
运筹学-单纯形法灵敏度对偶

运筹学-单纯形法灵敏度对偶

若新增约束如下：
max z 50x1 100x2 x1 x2 300 2x1 x2 400 x2 250 10x1 30x2 5000(电力约束) x1, x2 , 0
x1 x2 s1
把最优解x1=50,x2 =250代入电力约束 1050+30 250=80005000 新约束不满足,最优解变化
例题：已知某线性规划初始可行基是（S1 S2 S3 a1）， 最终单纯形表如下，求对偶价格不变时的△bi变化范围
x1 x2 s1
50 100 0
X1 50
1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0
0
1
Zj
50 100 0
δj
0
0
0
（1） △b1的变化范围： ?
（2） △b2的变化范围：?
（3） △b3的变化范围： ? （4） △b4的变化范围：?
1 0 1 2 0.5
B1 p6'
2
1
1
0.5
2
0 0 1 1.5 1.5
Z6' 50 0.5 0 (2) 100 1.5 175
' 6
C6
Z6'
150 175
25
δ6´<0，最优解不变，即仍生产Ⅰ50件，Ⅱ100件。
2、变量xk系数列由pk变为pk´，在最终单纯形表 上xk是基变量
x1 x2 s1
50 100 0
X1 50 1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0

运筹学灵敏度分析题

运筹学灵敏度分析题

运筹学灵敏度举例1．已知以下线性规划问题max z= 2x 1 +x 2-x 3 s.t. x 1 +2x 2 +x 3 ≤8 -x 1 +x 2 -2x 3≤4x 1,x 2,x 3≥0 的最优单纯形表如下：z x 1 x 5(1) 求使最优基保持不变的c 2=1的变化范围C 2 1+δ-1 0 0 0C B z 2 x 1 0x 53-δ≥0，δ≤3，即c 2≤4。

当c 2=5，即δ=4z x 1 8/2 x 512/3x2进基，x 1离基z x 2 x 5新的最优解为x 1=0，x 2=0，x 3=0，x 4=0，x 5=0，max z=20 (2) 对c 1=2进行灵敏度分析C 2+δ1 -1 0 0 0C B z 2+δ x 1 0x 53203020+≥+≥+≥⎧⎨⎪⎩⎪δδδ，δδδ≥-≥-≥-⎧⎨⎪⎩⎪3232/，当δ≥-3/2时，即c 1≥1/2时，最优基保持不变。

当c 1=4时，δ=4-2=2，最优基保持不变，最优解的目标函数制为z=16+8δ=32。

（3）增加一个新的变量x 6，c 6=4，a 612=⎡⎣⎢⎤⎦⎥。

[]z c c T666620124242-=-=⎡⎣⎢⎤⎦⎥-=-=-W aY B a 61610111213==⎡⎣⎢⎤⎦⎥⎡⎣⎢⎤⎦⎥=⎡⎣⎢⎤⎦⎥- 新的单纯形表为z x 1 x 5x 6进基，x 5离基z x 1 x 6新的最优解为x 1=4，x 2=0，x 3=0，x 4=0，x 5=0，x 6=4，max z=24。

（4）增加一个新的约束x 2+x 3≥2，求新的最优基和最优解。

z x 1 x 5 x 63/13/1用对偶单纯形法求解z xx x x x x RHSz x 1 x 5 x 2新的最优解为x 1=4，x 2=2，x 3=0，x 4=0，x 5=6，x 6=0，max z=10。

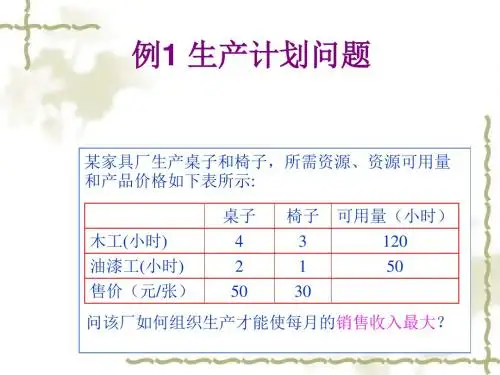
2．(1)利润最大化的线性规划模型为：max z= 25x1+12x2+14x3+15x4s.t. 3x1+2x2+x3+4x4≤24002x1+2x3+3x4≤3200x1+3x2+2x4≤1800x1, x2, x3, x4≥0单纯形表为：zx5x6x7x1进基，x5离基zx1x6x7x3进基，x6离基zx1x3x7x2进基，x1离基zx2x3x7最优解为：x1=0，x2=400，x3=1600，x4=0，x5=0，x6=0，x7=600，max z=27200即最优生产计划为：产品A不生产；产品B生产400万件；产品C生产1600万件；产品D不生产，最大利润：27200万元。

运筹学灵敏度分析

运筹学灵敏度分析

只需由 j 0解得c j的范围。
(2) c j 是基变量x j的价格系数 这时要影响所有的检验 数
i ci (c1 ci ci cm ) B Pi , 应由所有的 i 0解得公共的c j。
1
p11-2
例1：在（煤电油例）中，其单纯形终表如下：
0 x 7 x 12 x
3 1
运筹学
2

84 20 24
0 1 0
0
0 0 1
0
1 0 0
0
- 0.32 0.4 - 0.12
- 1.36
1.16 - 0.2 0.16
- 0.52
z 428
（1）甲产品的价格在何范围内变化时，现最优解不变？
解：甲产品的价格c1是基变量的价格系数。 0.32 由 4 0 0 7 c1 12 0.4 2.8 0.4c1 1.44 0 0.12 得 c 3.4， 1.16 由 5 0 0 7 c1 12 - 0.2 1.4 0.2c1 1.92 0 0.16 得 c 2.6，
2
运筹学
例1：在（煤电油例）中，其单纯形终表如下：
0 x 7 x 12 x
3
1
2

84 20 24
0 1
0
0 0 1
1 0
0
- 3.12 1.16 0.4 - 0.2
- 0.12 0.16
z 428
0
0
0
- 1.36
- 0.52
（3）若有人愿以每度1元的价格向该厂供应25度电，是 否值得接受？
§3.4 灵敏度分析
灵敏度分析——研究系数变化对最优解的影响.

运筹学教材编写组《运筹学》章节题库-对偶理论与灵敏度分析(圣才出品)

运筹学教材编写组《运筹学》章节题库-对偶理论与灵敏度分析(圣才出品)
3 / 36
圣才电子书 十万种考研考证电子书、题库视频学习平台

5．已知 Yi 为线性规划的对偶问题的最优解，若 Yi>0，说明（）。[深圳大学 2006 研] A．原问题的最优解 xi=0 B．在最优生产计划中第 i 种资源己完全耗尽 C．在最优生产计划中第 i 种资源有剩余 D．无法判断 【答案】B 【解析】当影子价格为 0 时，表示某种资源未得到充分利用；而当资源的影子价格不为 零时，表明该种资源在生产中已耗费完毕。
【答案】对偶单纯形法
3．某极小化线性规划问题的对偶问题的最优解的第 l 个分量为 yl=-12，则该问题的第 1 个约束条件的右端常数项的对偶价格为：______。[武汉大学 2006 研]
5 / 36
圣才电子书

【答案】-12
十万种考研考证电子书、题库视频学习平台
【解析】由对偶问题的经济解释可知，原问题约束条件的右端常数项的对偶价格等于对
4．根据对偶解的经济含义，若天然气资源是我国的一种稀缺能源资源，其影子价格必 然是（）。[北京科技大学 2010 研]
A．不能确定 B．＜0 C．=0 D．＞0 【答案】D 【解析】影子价格是对系统内部资源稀缺程度的一种客观评价，某种资源的影子价格越 高，说明该资源在系统内越稀缺，增加该资源的供应量对系统目标函数值贡献也越大。天然 气是资源是一种稀缺能源资源，其影子价格必然大于 0。
学 2008 研]
十万种考研考证电子书、题库视频学习平台
【答案】√
【解析】它的对偶问题可能无解，也可能有无界解。
二、选择题
1．用线性规划制定某一企业的生产计划问题，两种资源的影子价格分别为 y甲=5 ， y乙=8 ，说明这两种资源在该企业中的稀缺程度为（）。[北京交通大学 2010 研]

运筹学实验

运筹学实验

1、实验题目运筹学实验2-线性规划灵敏度分析某公司生产三种产品A1、A2、A3，它们在B1、B2两种设备上加工，并耗用C1、C2两种原材料，已知生产单位产品耗用的工时和原材料以及设备和原材料的最多可使用量如表 C －7所示。

表 C －7 生产三种产品的有关数据已知对产品A2的需求每天不低于70件，A3不超过240件。

经理会议讨论如何增加公司收入，提出了以下建议：（a ）产品A3提价，使每件利润增至60元，但市场销量将下降为每天不超过210件； （b ）原材料C2是限制产量增加的因素之一，如果通过别的供应商提供补充，每千克价格将比原供应商高20元；（c ）设备B1和B2每天可各增加40 min 的使用时间，但相应需支付额外费用各350元； （d ）产品A2的需求增加到每天100件；（e ）产品A1在设备B2上的加工时间可缩短到每件2 min ，但每天需额外支出40元。

分别讨论上述各条建议的可行性，哪些可直接利用“敏感性报告”中的信息，哪些需要重新规划求解2、模型设1X 为A1的产量，2X 为A2的产量，3X 为A3的产量1）数学模型由题目可建立线性规划模型：321502030max x x x z ++=)3,2,1(0240703004204460234302323212131321=≥≤≥≤++≤+≤+≤++i x x x x x x x x x x x x x i2）用Excel 建模求解3、实验结果及敏感性分析1）实验结果以得出题得最优解 x1=0,x2=70,x3=230 时，最优值为 12900，即生产 A1,A2，A3 产品分别是 0 件， 70 件，230 件时，公司可获得最大利润 12900 元2）敏感性报告①A3 产品每件利润提到 60 元，这在灵敏度分析的最优基不变范围 A3[50-23.3333，5 0+∞]内，但市场销量下降为不超过 210 件，而从求解报告中中最优解 A3=230 时，有最大目标值，故此建议可行。

运筹学灵敏度分析(最全版)PTT文档

运筹学灵敏度分析(最全版)PTT文档

c + c YP 表中b列中有负数，即解答列有负数，故可用对偶单纯形法求最优解。
1、代表产品的单位利润或单位售价时，灵敏j度分析可用于j 预先确定保j持现有生产规模条件下单位产品利润或单价的可变范围。
解题步骤：先用单纯形法解题，然后考虑参数变化，最后确定变化范围。
△c2/2≤0和△c2/8-1/8≤0
br bi / air ;
i=1，2，…，m i=1，2，…，m
air < 0
br bi / air
得到公式:
5=-8, △b2≤2/0.
ma ab ix irai{r0} brm iab inira{ ir0}
（2）当cr是基底变量xr的系数，即cr CB，cr变化 cr后，有
故△c2的变化范围:
例题: 将上面例题进行实际应用。每台设备台时的影子 价格为元。若该厂又从别处抽出4台时用于生产两种产品， 求这时该厂生产两种产品的最优方案。
表中b列中有负数，即解答列有负数，故可用对偶单纯 形法求最优解。
最优解见下表
cj
CB XB b 2 x1 4 0 x3 2 3 x2 3
cj-zj
230 0 0 x1 x2 x3 x4 x5 1 0 0 0.25 0 0 0 1 -0.25 -05 0 1 0 0 0.25 0 0 0 -0.5 -0.75
5=-8, △b2≤2/0.
2每台3设例备0台：时的0求影子0第价格一为元章。 例题中当第二个约束条件b2变化范围△b2。
△c2≥-1.
每台设备台时的影子价格为元。
设基变量x2的系数c2变化△c2，在原最优解不变的条件下，确定△c2的变化范围。
x1 x2 x3 x4 x5 0 0 1 -0.

运筹学24灵敏度分析

运筹学24灵敏度分析
非基变量的价格系数变化，在原最优解 不变的条件下，确定的变化范围。
（2）当cj是基变量的价值系数——它的变化 将影响所有非基变量的检验数.
N CN CB B 1 N 为当最cj优变解化，时否，如则能可保用持单纯 N形法0 继，续则迭当代前求解出仍 新的最优解。
将cj看作待定参数，令 N CN CB B1N 0
②（B-1b）i<0, 当前基为非可行基, 可用对偶单纯形法 求出新的最优解；
③如何求出保持最优基不变的bi的范围? 把bi看作待定参数,令B-1b≥0,求解该不等式组即可；
b发生变化， XB B1(b b)
X B B 1b
B1(b b) B1b B1b
B1b B1(0 , 0 ,L , 0 , br , 0 ,L , 0)T (a1r br ,L , air br ,L , amr br )T br (a1r ,L , air ,L , amr )T
（或消耗的资源量）和单位产品利润，设该种 产 品 的 产 量 为 xk， 则 ck 和 Pk 已 知 ， 需 要 进 行 “是否投产”的决策。
如果算出的σk<0,说明新产品D不宜 投产，否则会使产品总利润下降！
(2) 增加1个约束条件：
相当于系数阵A增加1行
首先将原最优解代入新增约束检查是 否满足？是，则说明新增约束不影响最 优解。否则再作下面的讨论：
将新增约束标准化，添加到原最优表 格中（相当于约束矩阵新增1行）；
进行规格化处理——用矩阵的行变换 将当前基变成单位阵；
用适当方法（通常是对偶单纯形法） 进行迭代求出新的最优解。
（3）其他情况讨论： 某个产品工艺参数改变； 新品代替原产品等；
bi air br ≥ 0 i 1 , 2 ,L , m

运筹学讲义影子价格-灵敏度分析-运输问题

运筹学讲义影子价格-灵敏度分析-运输问题

2)
0.000000
48.000000
3)
0.000000
2.000000
4) 40.000000
0.000000
35元可买到1桶牛奶，要买吗？ 35 <48, 应该买！
聘用临时工人付出的工资最多每小时几元？ 2元！
21
结果解释
DO RANGE(SENSITIVITY) ANALYSIS?
Yes
RANGES IN WHICH THE BASIS IS UNCHANGED: OBJ COEFFICIENT RANGES
20桶牛奶生产A1, 30桶生产A2，利润3360元。
18
模型求解
OBJECTIVE FUNCTION VALUE
1)
3360.000
VARIABLE VALUE REDUCED COST
X1 20.000000
0.000000
X2 30.000000
0.000000
ROW SLACK OR SURPLUS DUAL PRICES
16
1桶
12小时 3公斤A1
牛奶 或 8小时 4公斤A2
获利24元/公斤 获利16元/公斤
每天 50桶牛奶 时间480小时 至多加工100公斤A1
决策变量 目标函数
约束条件
x1桶牛奶生产A1 x2桶牛奶生产A2
获利 24×3x1
获利 16×4 x2
每天获利 Max z 72 x1 64 x2
原料供应
12
影子价格的经济意义：在资源得到最优配置，使总效益最大时，该资源投 入量每增加一个单位所带来总收益的增加量。
影子价格是一种静态的资源最优配置价格，不能表现资源在不同时期动态 配置时的最优价格，只反映某种资源的稀缺程度和资源与总体积极效益之间 的关系，不能代替资源本身的价值。

运筹学单纯形法的灵敏度分析

运筹学单纯形法的灵敏度分析
的产量就大于零，即需考虑生产丙产品了。
• 所以，丙产品单位利润的变动范围是c3<4；
• 讨论： • 假设此时c3增加到6元，产量应为多少？
C3已超出变动范围
• 代入单纯形表 最后一段 继续计算。
段
Cj ↓
→ 基
0 b
23 x1 x2
6 x3
0 0 Qi x4 x5
2
x1
1
1
0 （-1） 4 -1
0
0
-1 4 -1
1
2 -1 1
0
-3 -5 -1
Bi变化影响哪些因素？
• 当bi变化时，从单纯形法计算过程可知，它不影响检验数， 只影响b列本身，也就是说，它不影响基变量但会改变最优 解的具体数值，如上例中，假设b1发生变化，劳动力使用从 一个劳动力增加到2个劳动力，即b1=2，则
• ∵b变化不影响检验数 • ∴单纯形表最后一段基变量结构不变，仍是x1，x2，改变的
x5
Qi
0
x4
1
1
0
x5
3
Cj-Zj →
1/3
1/3 1/3 1
1/3 （4/3） 7/3 0
2
3
10
0
3
1 9/4 →
0
0
x4 1/4 （1/4）
0
-1/4 1 -1/4 1
→
2
3
x2 9/4 1/4
1 7/4 0 3/4 9
Cj-Zj →
5/4
0 -17/4 0 -9/4
2
x1
1
1
3
3
x2
2
0
Cj-Zj → -8
5b1 3
分析

运筹学课件 灵敏度分析举例

运筹学课件 灵敏度分析举例

x2
1 0
x3
1 -1/2
x4
-2 3/2

20 x1 15
j cj z j
CB
30 50
cj xB
50
30
0
0
35 0 x1 7.5 1 j c j z j 1425 0
x2
b
x1
x2
1 0 0
x3
x4

1/2 -1/2 -1/4 3/4 -2.5 -22.5

木工用量 4 x1 3x2 120 木工可使用量 油漆工用量 负条件。
2 x1 x2 50 油漆工可使用量 决策变量还应当满足 x 0 ， x2 0，叫做非 1
例1的数学模型
max z 50x1 30x2
s.t.
4 x1 3x2 120 2 x1 x2 50 x1 , x2 0
x3
1
0
x4
0
1

30
25
x4
j cj z j
0
50
30
0
0
第一次换基并求解
CB
0 50
x3 x1
cj xB b
20 25 1250
50
30
0
x1
0 1 0
x2
（1） 1/2 5
x3
1 0 0
x4
-2 1/2 -25 20 50
0
j cj z j
第二次换基和求解
cj xB
50 30 0 0
CB
30 50
x2
b
x1
0 1 0
x2
1 0 0

《运筹学》第三章线性规划对偶理论与灵敏度分析习题及答案

《运筹学》第三章线性规划对偶理论与灵敏度分析习题及答案

《运筹学》第三章线性规划对偶理论与灵敏度分析习题及答案一、填空题1. 在线性规划问题中，若原问题存在最优解，则其对偶问题也一定存在最优解，这是线性规划的基本性质之一，称为______。

答案：对偶性2. 在线性规划问题中，若原问题与对偶问题均存在可行解，则它们均有______。

答案：最优解3. 对于线性规划问题，若原问题约束条件系数矩阵为A，目标函数系数向量为c，则其对偶问题的目标函数系数向量是______。

答案：c的转置（c^T）二、选择题1. 线性规划的原问题与对偶问题之间的关系是：A. 原问题的最优解和对偶问题的最优解相同B. 原问题的最优解是对偶问题的最优解的负数C. 原问题的最优解与对偶问题的最优解互为对偶D. 原问题的最优解和对偶问题的最优解没有关系答案：C2. 在线性规划中，若原问题不可行，则其对应的对偶问题：A. 可行B. 不可行C. 无界D. 无法确定答案：B三、判断题1. 线性规划的原问题和对偶问题具有相同的可行解。

（）答案：错误2. 若线性规划的原问题存在唯一最优解，则其对偶问题也一定存在唯一最优解。

（）答案：正确四、计算题1. 已知线性规划问题：max z = 3x1 + 2x2s.t.x1 + 2x2 ≤ 42x1 + x2 ≤ 5x1, x2 ≥ 0求该问题的对偶问题，并求解原问题和对偶问题的最优解。

答案：对偶问题为：min w = 4y1 + 5y2s.t.y1 + 2y2 ≥ 32y1 + y2 ≥ 2y1, y2 ≥ 0原问题和对偶问题的最优解如下：原问题最优解：x1 = 2, x2 = 1，最大利润z = 8对偶问题最优解：y1 = 2, y2 = 1，最小成本w = 82. 某工厂生产甲、乙两种产品，生产一件甲产品需要2小时的机器时间和3小时的工人劳动时间，生产一件乙产品需要1小时的机器时间和1小时的工人劳动时间。

工厂每周最多能使用12小时的机器时间和9小时的工人劳动时间。

运筹学第二章灵敏度分析

运筹学第二章灵敏度分析

CB
-3 -5 -Z’
xB x1 X2
2.4 对偶解的经济解释
一、对偶线性规划 的解： P55
Cj xB x3 x1 x2 z b 7/2 7/2 3/2 x1 1 0 0 y4 Cj yB b y1 15/2 0 原问题变量 x2 0 0 1 0 y5 对偶问题变量 y2 y3 x3 1 0 0 0 y1 原问题变量 x4 5/4 1/4 -1/4 1/4 y2 x5 -15/2 -1/2 3/2 1/2 y3
T.G.Koopman（库普曼）和 L.V.Kamtorovich（康脱罗维奇）
二人因此而共同分享了1975年的第7届诺贝尔经 济学奖。
2.5 灵敏度分析
一、灵敏度分析的含义 是指系统或事物因周围条件变化显示出来的敏感性程度的分析。 对于线性规划问题的灵敏度分析是指参数A，b，C变化引起的 对原问题解的变化的分析。 其中：A为技术参数矩阵，b为资源向量，C为价值向量 可以用参数变化后的问题重新用单纯形法求解？ 没必要，意义不大，有些问题看不出来。 把相应的变化反映到最终单纯形表中，再根据情况用相应的方 法求解。
Z 50 x1 30 x2
2.1 线性规划的对偶问题与对偶理论
假设现有乙公司准备租借用(购买)该木器厂的木工和 油漆工两种劳力的劳务，需要考虑这两种劳务以什么 样的价格租入最合算？而同时甲公司要以什么条件才 会租让？甲公司肯定会以自己利用两种劳力的劳务组 织生产所获得的利润最大为条件，设每个木工的租用 价格为y1，每个油漆工的租用价格为y2，则乙公司愿 意租用的出资为：
0 变量 0 无限制
型 约束 型 型
0 变量 0 无限制
型 约束 型 型

《运筹学》 第三章线性规划对偶理论与灵敏度分析习题及 答案

《运筹学》 第三章线性规划对偶理论与灵敏度分析习题及 答案

第三章线性规划对偶理论与灵敏度分析习题 一、思考题1．对偶问题和对偶变量的经济意义是什么？2．简述对偶单纯形法的计算步骤。

它与单纯形法的异同之处是什么？3．什么是资源的影子价格？它和相应的市场价格之间有什么区别？4．如何根据原问题和对偶问题之间的对应关系，找出两个问题变量之间、解及检 验数之间的关系？5．利用对偶单纯形法计算时，如何判断原问题有最优解或无可行解？6．在线性规划的最优单纯形表中，松弛变量（或剩余变量）0>+k n x ，其经济意 义是什么？7．在线性规划的最优单纯形表中，松弛变量k n x +的检验数0>+kn σ（标准形为求最小值），其经济意义是什么？8．将i j ji bc a ,,的变化直接反映到最优单纯形表中，表中原问题和对偶问题的解 将会出现什么变化？有多少种不同情况？如何去处理？ 二、判断下列说法是否正确1．任何线性规划问题都存在且有唯一的对偶问题。

2．对偶问题的对偶问题一定是原问题。

3．若线性规划的原问题和其对偶问题都有最优解，则最优解一定相等。

4．对于线性规划的原问题和其对偶问题，若其中一个有最优解，另一个也一定 有最优解。

5．若线性规划的原问题有无穷多个最优解时，其对偶问题也有无穷多个最优解。

6．已知在线性规划的对偶问题的最优解中，对偶变量0>*i y ，说明在最优生产计 划中，第i 种资源已经完全用尽。

7．已知在线性规划的对偶问题的最优解中，对偶变量0=*i y ，说明在最优生产计 划中，第i 种资源一定还有剩余。

8．对于i j ji bc a ,,来说，每一个都有有限的变化范围，当其改变超出了这个范围 之后，线性规划的最优解就会发生变化。

9．若某种资源的影子价格为u ，则在其它资源数量不变的情况下，该资源增加k 个单位，相应的目标函数值增加 u k 。

10．应用对偶单纯形法计算时，若单纯形表中某一基变量0<i x ，且i x 所在行的 所有元素都大于或等于零，则其对偶问题具有无界解。

运筹学2对偶理论与灵敏度分析

运筹学2对偶理论与灵敏度分析

三、增加新变量的灵敏度分析
在管理中经常遇到的问题：已知一 种新产品的技术经济指标，在原有最优 生产计划的基础上，怎样最方便地决定 该产品是否值得投入生产，可在原线性 规划中引入新的变量 ； 无论增加什么样的新变量，新问题 的目标函数只能向好的方向变化。
例2.16 （续例2.14）
设企业研制了一种新产品，对三种资源的消耗系数 列向量以P6表示。试问它的价值系数c6符合什么条件， 才必须安排它的生产？设c6=3，新的最优生产计划是 什么？
1. 强制生产30件A x1 必须等于30 目 标值下降; 下降程度可用 x1 的检验数进行 计算：
cj CB 0 5 4 0 XB x3 x1 x2 x6 σ
j
5 b 25 35 10 150 x1 0 1 0 4 0
4 x2 0 0 1 2 0
0 x3 1 0 0 0 0
0 x4 2 1 -1 0 -1
0 x5 -5 -1 2 0 -3
0 x6 0 0 0 1 0
0 5 4 0
0 5 4 0
90 1 = 80 0 b 0 3
250 - 5b3 - 5 90 80 = 80 b 3 ≥0 1 1 80 2b b3 -1 2 3
2
解得40≤b3≤50，即当3∈[40，50]时，最优基B不变， 最优解为： * x3 250- 5b3 * x1 80 b 3 * = x2 80 2b 3
x4*=x5*=0, z*=5×(80－b3)+4×(－80+2b3)=80+3b3
例2.14 某企业利用三种资源生产两种产品 的最优计划问题归结为下列线性规划

运筹学：对偶理论与灵敏度分析习题与答案

运筹学：对偶理论与灵敏度分析习题与答案

一、填空题1、对偶问题的对偶问题是（）。

正确答案：原问题2、若X﹡和Y﹡分别是线性规划的原问题和对偶问题的最优解，则有CX﹡（）Y﹡b。

正确答案：=3、若X、Y分别是线性规划的原问题和对偶问题的可行解，则有CX（）Yb。

正确答案：<=4、若X﹡和Y﹡分别是线性规划的原问题和对偶问题的最优解，则有CX﹡（）Y*b。

正确答案：=5、设线性规划的原问题为maxZ=CX，Ax≤b，X≥0，则其对偶问题为（）。

正确答案：min=Yb YA>=c Y>=06、影子价格实际上是与原问题各约束条件相联系的（）的数量表现。

正确答案：对偶变量7、线性规划的原问题的约束条件系数矩阵为A，则其对偶问题的约束条件系数矩阵为（）。

正确答案：AT8、在对偶单纯形法迭代中，若某bi<0，且所有的aij≥0(j=1，2，…n)，则原问题（）。

正确答案：无解二、选择题1、线性规划原问题的目标函数为求极小值型，若其某个变量小于等于0，则其对偶问题约束条件为（）形式。

A. “≥”B. “≤”C. “>”D. “=”正确答案：A2、如果z*是某标准型线性规划问题的最优目标函数值，则其对偶问题的最优目标函数值w﹡满足（）。

A.W﹡=Z﹡B.W﹡≠Z﹡C.W﹡≤Z﹡D.W﹡≥Z﹡正确答案：A3、如果某种资源的影子价格大于其市场价格，则说明（）。

A.该资源过剩B.该资源稀缺C.企业应尽快处理该资源D.企业应充分利用该资源，开辟新的生产途径正确答案：B4、线性规划原问题的目标函数为求极小值型，若其某个变量小于等于0，则其对偶问题约束条件为（）形式。

A.≥B.≤C. >D. =正确答案：A5、对偶单纯形法的迭代是从（）开始的。

A.正则解B.最优解C.可行解D.可行解正确答案：A6、如果某种资源的影子价格大于其市场价格，则说明（）。

A.该资源过剩B.该资源稀缺C.企业应尽快处理该资源D.企业应充分利用该资源，开辟新的生产途径正确答案：B7、线性规划灵敏度分析的主要功能是分析线性规划参数变化对（）的影响。

运筹学灵敏度分析目标规划

运筹学灵敏度分析目标规划

3 灵敏度分析
例3 7:
例3 4增加3x1+ 2x2≤15;原最优解不 满足这个约束 于是
Ci
2 3000
0
CB XB b X1 X2 X3 X4 X5
X6
2 X1 4 1 0 0 1/4 0
0
0 X5 4 0 0 -2 1/2 1
0
3 X2 2 0 1 1/2 -1/8 0
0
0 X6 -1 0 0 -1 -1/2 0
故恒有d+×d=0
目标规划问题及其数学模型
2 统一处理目标和约束
对有严格限制的资源使用建立系统约束;数学形式同线性规划中 的约束条件 如C和D设备的使用限制
4 x 1 16 4 x 2 12
对不严格限制的约束;连同原线性规划建模时的目标;均通过目 标约束来表达 1例如要求甲 乙两种产品保持1:1的比例;系统约束表达为： x1=x2 由于这个比例允许有偏差; 当x1<x2时;出现负偏差d;即： x1+d =x2或x1x2+d =0 当x1>x2时;出现正偏差d+;即： x1d+ =x2或x1x2d+ =0
-z
m
f
0…
m
0 σm+1 … σn
其中：f = ∑ ci bi’ j = cj ∑ ci aij’ 为检验数 向量 b’ = B1 b
i=1
i=1
A= p1; p2; …; pn ; pj’ = B1 pj; pj’ = a1j’ ; a2j’ ; … ; amj’ T ; j = m+1; … ; n
0
0
-1.5-ΔC2/2 -1/8+ΔC2/8
0
σj=cjc1×a1j+c5 × a5j+c2+Δc2 ×a2jj=3;4 可得到 3≤Δc2≤1时;原最优解不变
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

运筹学灵敏度举例
1．已知以下线性规划问题
max z= 2x 1 +x 2
-x 3 s.t. x 1 +2x 2 +x 3 ≤8 -x 1 +x 2 -2x 3
≤4
x 1,
x 2,
x 3
≥0 的最优单纯形表如下：
z x 1 x 5
(1) 求使最优基保持不变的c 2=1的变化范围
C 2 1+δ
-1 0 0 0
C B z 2 x 1 0
x 5
3-δ≥0，δ≤3，即c 2≤4。

当c 2=5
，即δ=4
z x 1 8/2 x 5
12/3
x
2进基，x 1离基
z x 2 x 5
新的最优解为x 1=0，x 2=0，x 3=0，x 4=0，x 5=0，max z=20 (2) 对c 1=2进行灵敏度分析
C 2+δ
1 -1 0 0 0
C B z 2+δ x 1 0
x 5
3203020+≥+≥+≥⎧⎨⎪⎩⎪δδδ，δδδ≥-≥-≥-⎧⎨⎪
⎩
⎪3232/，当δ≥-3/2时，即c 1≥1/2时，最优基保持不变。

当c 1=4时，δ=4-2=2，最优基保持不变，最优解的目标函数制为z=16+8δ=32。

（3）增加一个新的变量x 6，c 6=4，a 612=⎡⎣⎢⎤⎦
⎥。

[]
z c c T
666620124242-=-=⎡⎣⎢⎤
⎦
⎥-=-=-W a
Y B a 61
610111213==⎡⎣⎢⎤⎦⎥⎡⎣⎢⎤⎦⎥
=⎡⎣⎢⎤
⎦
⎥- 新的单纯形表为
z x 1 x 5
x 6进基，x 5离基
z x 1 x 6
新的最优解为x 1=4，x 2=0，x 3=0，x 4=0，x 5=0，x 6=4，max z=24。

（4）增加一个新的约束x 2+x 3≥2，求新的最优基和最优解。

z x 1 x 5 x 6
3/1
3/1
用对偶单纯形法求解
z x
x x x x x RHS
z x 1 x 5 x 2
新的最优解为x 1=4，x 2=2，x 3=0，x 4=0，x 5=6，x 6=0，max z=10。

2．
(1)利润最大化的线性规划模型为：
max z= 25x1+12x2+14x3+15x4
s.t. 3x1+2x2+x3+4x4≤2400
2x1+2x3+3x4≤3200
x1+3x2+2x4≤1800
x1, x2, x3, x4≥0
单纯形表为：
z
x5
x6
x7
x1进基，x5离基
z
x1
x6
x7
x3进基，x6离基
z
x1
x3
x7
x2进基，x1离基
z
x2
x3
x7
最优解为：x1=0，x2=400，x3=1600，x4=0，x5=0，x6=0，x7=600，max z=27200
即最优生产计划为：产品A不生产；产品B生产400万件；产品C生产1600万件；产品D不生产，最大利润：27200万元。

原料甲：耗用2400吨，没有剩余；原料乙：耗用3200吨，没有剩余；原料丙：耗用1200吨，剩余600吨。

（问三种原料的利用率？）
（2） 产品A 利润变化范围： -C -25+δ -12 -14 -15 0 0 0 0
-C B z -12 x 2 -14 x 3 0
x 7
-1-δ≤0，δ≥-1，-c 1’=-c 1+δ≥-25-1=-26，即c 1≤26（万元/万件）
产品B 利润变化范围： -C -25 -12+δ -14 -15 0 0 0 0
-C B
z
-12+δ x 2 -14 x 3 0
x 7
--≤-+≤-+≤--≤⎧⎨
⎪⎪⎩⎪⎪102154061204140δδδδ///，δδδδ≥-≤≤≥-⎧⎨⎪⎪
⎩⎪⎪18451216
/，-1≤δ≤12，-13≤-12+δ≤0，-13≤-c 2’≤
0， 即：0≤c 2’≤13。

产品C 利润的变化范围： -C -25 -12 -14+δ -15 0 0 0 0 -C B z -12
x 2
-14+δ x 3
0 x 7
--≤-+≤-+≤⎧⎨⎪⎩⎪10213204120δδδ//，δδδ≥-≤≤⎧⎨⎪⎩
⎪1148 -1≤δ≤8，-15≤-14+δ≤-6，-15≤-c 3’≤-6，6≤c 3’≤15
产品D 的变化范围 -C -25 -12 -14 -15+δ
0 0 0 0 z x
x x x x x x RHS -C B z -12 x 2 -14 x 3 0
x 7
-21-δ≤0，δ≥-21，-15+δ≥-36，-c 4’≥-36，c 4’≤36。

（3） 求三种原料的影子价格和四种产品的机会成本
由最优单纯形表可知，原料甲、乙、丙的影子价格分别为：
6万元/吨、4万元/吨、0万元/吨。

产品A 、B 、C 、D 的机会成本分别为（
∑=m
i ij
i a
q 1
）：
26万元/万件、12万元/万件、14万元/万件、36万元/万件。

产品A 、D 在最优解中不安排生产的原因是机会成本大于利润。

（4） 在最优解中，原料甲的影子价格（6万元/吨）最大，因此这种原料最紧缺。

如果原料A 增加120吨，最优单纯形表的右边常数成为：
B b -'=--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥+⎡⎣⎢⎢⎢⎤⎦
⎥
⎥⎥=
⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥+-⎡⎣⎢⎢⎢⎤
⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎤
⎦
⎥⎥⎥≥11214001203234124001203200180040016006006000180100016004200///// 因此最优基保持不变，影子价格不变，原料的紧缺程度不变。