第四讲异方差和自相关学习资料

自相关和异方差处理顺序引言自相关和异方差是时间序列分析中常见的两种问题，它们影响了模型的准确性和可靠性。

在进行时间序列建模时，需要处理这些问题，以确保模型的有效性。

本文将深入探讨自相关和异方差处理的顺序，并讨论不同处理顺序的影响。

什么是自相关和异方差自相关自相关是指时间序列中当前观测值与之前观测值之间的相关性。

它衡量的是时间序列中各个观测值之间的依赖关系。

自相关可以用自相关函数（ACF）图来表示，通过观察ACF图，可以判断时间序列是否存在自相关。

异方差异方差是指时间序列中方差不稳定的特征。

在时间序列中，方差可能随着时间的推移发生变化，这会导致模型的拟合不准确。

异方差可以用方差函数（VCF）图来表示，通过观察VCF图，可以判断时间序列是否存在异方差。

自相关和异方差处理的重要性自相关和异方差对时间序列建模的准确性和可靠性有重要影响，它们需要被处理以获得可靠的模型结果。

•自相关的存在会导致参数估计不准确，预测结果失真。

如果存在自相关，模型会无法捕捉到序列的真实动态，导致预测结果不准确。

•异方差使得模型的残差不符合正态分布，违背了建模的基本假设。

这会使得模型的显著性检验和置信区间估计不可靠，影响模型的有效性。

因此，为了获得可靠的模型结果，需要对自相关和异方差进行处理。

自相关和异方差处理顺序的影响自相关和异方差的处理顺序会对最终的模型结果产生影响。

不同的处理顺序可能导致不同的模型结构和参数估计。

先处理自相关后处理异方差如果先处理自相关再处理异方差，可能会导致如下影响：1.自相关处理可能会改变时间序列的动态特征。

当我们去除自相关时，可能会削弱序列中的一些重要信息，导致模型无法准确捕捉到序列的动态变化。

2.异方差处理可能会影响自相关的结构。

当我们对残差进行异方差处理时，可能会改变残差序列的结构，从而使得自相关的估计失真。

先处理异方差后处理自相关如果先处理异方差再处理自相关，可能会产生如下影响：1.异方差处理可能改变原始序列的动态特征。

第六章异方差与自相关第一节异方差与自相关的定义一、例子例1，研究我国制造业利润函数，选取销售收入作为解释变量，数据为1998年的食品年制造业、饮料制造业等28个截面数据（即n=28）。

数据如下表，其中Y表示制造业利润函数，X表示销售收入（单位为亿元）。

Y对X的散点图为从散点图可以看出，在线性的基础上，有的点分散幅度较小，有的点分散幅度较大。

因此，这种分散幅度的大小不一致，可以认为是由于销售收入的影响，使得制造业利润偏离均值的程度发生了变化，而这种偏离均值的程度大小不同是一种什么现象？如何定义？下面给出制造业利润对销售收入的回归估计。

模型的书写格式为2ˆ12.03350.1044(0.6165)(12.3666)0.8547,..84191.34,152.9322213.4639,146.4905Y YX R S E F Y s =+=====通过变量的散点图、参数估计、残差图，可以看出尽管表面上模型的估计效果还不错，但随机误差（残差）可能存在一种系统性的表现。

例2，研究中国城镇居民消费函数，其中选取了两个变量，城镇家庭商品性支出（现价）和城镇家庭可支配收入（现价），分别记为CSJTZC 和CSJTSR ，时间从1978年到1997年，n=20。

但为了剔除物价的影响，分别对CSJTZC 和CSJTSR 除以物价（用CPI 表示），这里CPI 为城镇居民消费物价指数（以1990年为100%），经过扣除价格因素以后，记CPICSJTSRX CPICSJTZCY ==即如下表回归以后得到的残差为Dependent Variable: Y Method: Least Squares Date: 10/27/04 Time: 09:39 Sample: 1978 1997 Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. C -103.3692 78.80739 -1.311669 0.2061 X0.9235510.01603357.603880.0000 R-squared0.994605 Mean dependent var 3939.341 Adjusted R-squared 0.994305 S.D. dependent var 2124.467 S.E. of regression 160.3247 Akaike info criterion 13.08692 Sum squared resid 462671.9 Schwarz criterion 13.18649 Log likelihood -128.8692 F-statistic 3318.207 Durbin-Watson stat1.208037 Prob(F-statistic)0.000000通过残差图可以看出，残差有随时间的系统性表现。

七、 异方差与自相关一、背景我们讨论如果古典假定中的同方差和无自相关假定不能得到满足，会引起什么样的估计问题呢？另一方面，如何发现问题，也就是发现和检验异方差以及自相关的存在性也是一个重要的方面，这个部分就是就这个问题进行讨论。

二、知识要点1、引起异方差的原因及其对参数估计的影响2、异方差的检验（发现异方差）3、异方差问题的解决办法4、引起自相关的原因及其对参数估计的影响5、自相关的检验（发现自相关）6、自相关问题的解决办法 （时间序列部分讲解） 三、要点细纲1、引起异方差的原因及其对参数估计的影响原因：引起异方差的众多原因中，我们讨论两个主要的原因，一是模型的设定偏误，主要指的是遗漏变量的影响。

这样，遗漏的变量就进入了模型的残差项中。

当省略的变量与回归方程中的变量有相关关系的时候，不仅会引起内生性问题，还会引起异方差。

二是截面数据中总体各单位的差异。

后果：异方差对参数估计的影响主要是对参数估计有效性的影响。

在存在异方差的情况下，OLS 方法得到的参数估计仍然是无偏的，但是已经不具备最小方差性质。

一般而言，异方差会引起真实方差的低估，从而夸大参数估计的显著性，即是参数估计的t 统计量偏大，使得本应该被接受的原假设被错误的拒绝。

2、异方差的检验 （1）图示检验法由于异方差通常被认为是由于残差的大小随自变量的大小而变化，因此，可以通过散点图的方式来简单的判断是否存在异方差。

具体的做法是，以回归的残差的平方2i e 为纵坐标，回归式中的某个解释变量i x 为横坐标，画散点图。

如果散点图表现出一定的趋势，则可以判断存在异方差。

（2）Goldfeld-Quandt 检验Goldfeld-Quandt 检验又称为样本分段法、集团法，由Goldfeld 和Quandt 1965年提出。

这种检验的思想是以引起异方差的解释变量的大小为顺序，去掉中间若干个值，从而把整个样本分为两个子样本。

用两个子样本分别进行回归，并计算残差平方和。

1.5 假定条件的不成立用OLS 法得到的估计模型通过统计检验后，还要检验摸型是否满足假定条件。

由1.3 节知，只有模型的4个假定条件都满足时，用OLS 法得到的估计量才具有最佳线性无偏特性。

当一个或多个假定条件不成立时，OLS 估计量将丧失上述特性。

本节讨论当假定条件不成立时，对参数估计带来的影响以及相应的补救措施。

以下讨论都是在某一个假定条件被违反，而其他假定条件都成立的情况下进行。

分为5个步骤。

（1）回顾假定条件。

（2）假定条件不成立对模型参数估计带来的影响。

（3）定性分析假定条件是否成立。

（4）假定条件是否成立的检验（定量判断）。

（5）假定条件不成立时的补救措施。

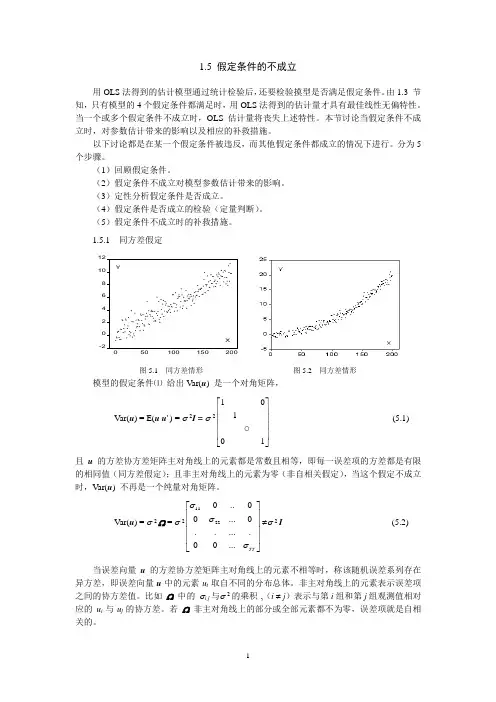
1.5.1 同方差假定-224681012050100150200XY图5.1 同方差情形 图5.2 同方差情形模型的假定条件⑴ 给出V ar(u ) 是一个对角矩阵， Var(u ) = E(u u ' ) = σ 2I = σ 21011⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(5.1) 且u 的方差协方差矩阵主对角线上的元素都是常数且相等，即每一误差项的方差都是有限的相同值（同方差假定）；且非主对角线上的元素为零（非自相关假定），当这个假定不成立时，Var(u ) 不再是一个纯量对角矩阵。

Var(u ) = σ 2 Ω = σ 211220..00...0 00...TT σσσ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦≠σ 2 I (5.2)当误差向量u 的方差协方差矩阵主对角线上的元素不相等时，称该随机误差系列存在异方差，即误差向量u 中的元素u t 取自不同的分布总体。

非主对角线上的元素表示误差项之间的协方差值。

比如 Ω 中的 σi j 与σ 2的乘积 ,（i ≠ j ）表示与第i 组和第j 组观测值相对应的u i 与 u j 的协方差。

若 Ω 非主对角线上的部分或全部元素都不为零，误差项就是自相关的。

本节讨论异方差。

下一节讨论自相关问题。

《计量经济学》中多重共线性、异方差性、自相关三者之间的联系与区别首先我们先来回顾一下经典线性回归模型的基本假设：1、为什么会出现异方差性我们可以从一下两方面来分析：第一，因为随即误差项包括了测量误差和模型中被省略的一些因素对因变量的影响；第二，来自不同抽样单元的因变量观察值之间可能差别很大。

因此，异方差性多出现在截面样本之中。

至于时间序列，则由于因变量观察值来自不同时期的同一样本单元，通常因变量的不同观察值之间的差别不是很大，所以异方差性一般不明显。

含义及影响:y=X β+ε，var(εi )var(εj ), ij ，E(ε)=0，或者记为212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭即违背假设3。

用OLS 估计，所得b 是无偏的，但不是有效的。

111(')'(')'()(')'b X X X y X X X X X X X βεβε---==+=+由于E(ε)=0，所以有E(b )=β。

即满足无偏性。

但是，b 的方差为1111121var(|)[()()'][(')''(')|] (')'['|](') (')'()(')b X E b b E X X X X X X X X X X E X X X X X X X X X X ββεεεεσ------=--===Ω其中212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭2、自相关产生的原因：（1）、经济数据的固有的惯性带来的相关 （2）、模型设定误差带来的相关 （3）、数据的加工带来的相关 含义及影响:cov(,)0,i j i j εε≠≠影响：和异方差一样，系数的ls 估计是无偏的，但不是有效的。

D －W 检验（Durbin －Watson ）221212222121212222112112122211221122121()()()2()()222222(1)n i i i n i i n n n i i i i i i i n i i n n n i i i i i i i n n i i n i i i nn n i i i i nn i ie e d e e e e e e e e e e e e e e e e e e e e e e ρρ=-===-=-====-==-===∑-=∑∑+∑-∑=∑∑+∑-∑--=∑∑+=--∑∑+=--∑≈-其中2121n i i i n i ie e e ρ=-=∑=∑是样本一阶自相关函数。

自相关和异方差处理顺序在统计学和计量经济学中，自相关和异方差是两个常见的问题，需要进行相应的处理才能保证模型的准确性和可靠性。

本文将以人类的视角，采用准确的中文进行描述，详细介绍自相关和异方差的处理顺序及其重要性。

一、自相关处理自相关是指时间序列数据中观测值之间存在的相关性。

当序列中的观测值之间存在一定的相关性时，会导致统计模型的参数估计不准确，假设检验无效，预测结果不可靠。

因此，需要进行自相关的处理。

自相关处理的一种常见方法是使用自相关函数（ACF）和偏自相关函数（PACF）进行分析。

ACF表示观测值与不同滞后期的观测值之间的相关性，PACF表示观测值与滞后期观测值之间的相关性，探究观测值之间的相关性结构。

在进行自相关处理时，可以采取以下步骤：1. 绘制时间序列图，观察序列的趋势和波动性。

2. 进行序列的平稳性检验，确保序列满足平稳性的要求。

3. 绘制ACF和PACF图，分析观测值之间的相关性结构。

4. 根据ACF和PACF的图形特征，选择合适的自回归移动平均模型（ARMA模型）。

5. 估计模型参数，进行模型拟合。

6. 检验模型的残差序列是否存在自相关，如果存在，则返回第3步，重新选择模型。

通过以上步骤，可以有效地处理自相关问题，提高模型的准确性和可靠性。

二、异方差处理异方差是指随着自变量的变化，因变量的方差也发生变化。

当存在异方差时，会导致模型的参数估计不准确，假设检验无效，预测结果不可靠。

因此，需要进行异方差的处理。

异方差处理的一种常见方法是使用加权最小二乘法（Weighted Least Squares, WLS）。

WLS是一种在回归分析中常用的方法，通过对误差项进行加权，降低异方差对回归结果的影响。

在进行异方差处理时，可以采取以下步骤：1. 绘制残差图，观察残差的分布特征。

2. 进行异方差检验，判断是否存在异方差。

3. 如果存在异方差，可以使用加权最小二乘法进行回归估计。

4. 根据异方差的特点，选择合适的加权函数，对误差项进行加权。