2018年上海市业余数学学校招生试卷

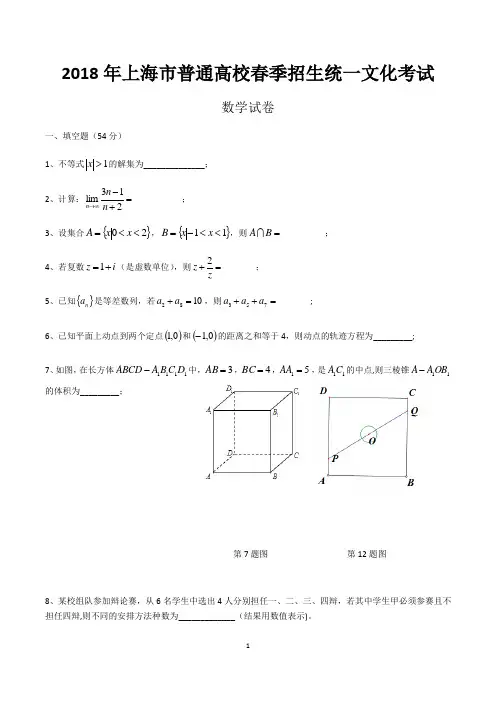
2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题（54分）1、不等式1>x 的解集为______________；2、计算：_________213lim=+-∞→n n n ；3、设集合{}20<<=x x A ，{}11<<-=x x B ，则________=B A ；4、若复数i z +=1（是虚数单位），则______2=+zz ； 5、已知{}n a 是等差数列，若1082=+a a ，则______753=++a a a ;6、已知平面上动点到两个定点()0,1和()0,1-的距离之和等于4，则动点的轨迹方程为_________;7、如图，在长方体1111D C B A ABCD -中，3=AB ，4=BC ，51=AA ，是11C A 的中点,则三棱锥11OB A A -的体积为_________；第7题图 第12题图8、某校组队参加辩论赛，从6名学生中选出4人分别担任一、二、三、四辩，若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________（结果用数值表示)。

9、设R a ∈，若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等，则_______=a ；10、设R m ∈，若是关于的方程0122=-++m mx x 的一个虚根，则-z 的取值范围是________;11、设0>a ，函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点，则的取值范围是__________；12、如图,在正方形ABCD 的边长为米，圆的半径为1米,圆心是正方形的中心,点、分别在线段AD 、上,若线段PQ 与圆有公共点，则称点在点的“盲区”中，已知点以1。

5米/秒的速度从出发向移动,同时，点以1米/秒的速度从出发向移动，则在点从移动到的过程中,点在点的盲区中的时长均为_____秒(精确到0。

2018年普通高等学校招生全国统一考试（上海卷）数学一、选择题（本大题共4小题，共20.0分）1.设P上的动点，则P到该椭圆的两个焦点的距离之和为（）A. B. C. D.2.已知a∈R，则“a＞11”的（）A. 充分非必要条件B. 必要非充分条件充要条件 D. 既非充分又非必要条件3.棱锥为阳马，设该正六棱柱的顶点为顶点、以A. 4B. 8C. 12D. 164.设D是含数1的有限实数集，f（x）是定义在D上的函数，若f（x）的图象绕原点f（1）的可能取值只能是（）D. 0二、填空题（本大题共12小题，共54.0分）5.______．6.-y2=1的渐近线方程为______．7.在（1+x）7的二项展开式中，x2项的系数为______（结果用数值表示）．8.设常数a∈R，函数f（x）=1og2（x+a）．若f（x）的反函数的图象经过点（3，1），则a=______．9.已知复数z满足（1+i）z=1-7i（i是虚数单位），则|z|=______．10.记等差数列{a n}的前n项和为S n，若a3=0，a6+a7=14，则S7=______．11.已知α∈{-2，-1，1，2，3}，若幂函数f（x）=xα为奇函数，且在（0，+∞）上递减，则α=______．12.在平面直角坐标系中，已知点A（-1，0）、B（2，0），E、F是y轴上的两个动点，______．13.有编号互不相同的五个砝码，其中5克、3克、1克砝码各一个，2克砝码两个，从中随机选取三个，则这三个砝码的总质量为9克的概率是______（结果用最简分数表示）．14.设等比数列{a n}的通项公式为a n=q n-1（n∈N*），前n项和为S nq=______．15.已知常数a＞0，函数f（x P（p，，Q（q，．若2p+q=36pq，则a=______．16.已知实数x1、x2、y1、y2满足：x12+y12=1，x22+y22=1，x1x2+y1y2的最大值为______．三、解答题（本大题共5小题，共76.0分）17.已知圆锥的顶点为P，底面圆心为O，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图．求异面直线PM与OB所成的角的大小．18.为偶函数，求a的值；19.某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时，某地上班族S中的成员仅以自驾或者公交方式通勤，分析显示：当S中x%(0<x<100)的成员自驾时，（单位：分钟），而公交群体的人均通勤时间不受x影响，恒为40分钟，试根据上述分析结果回答下列问题：（1）当x在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？（2）求该地上班族S的人均通勤时间g(x)的表达式；讨论g(x)的单调性，并说明其实际意义．20.设常数t＞2．在平面直角坐标系xOy中，已知点F（2，0），直线l：x=t，曲线Γ：y2=8x（0≤x≤t，y≥0）．l与x轴交于点A、与Γ交于点B．P、Q分别是曲线Γ与线段AB上的动点．（1）用t表示点B到点F的距离；（2）设t=3，|FQ|=2，线段OQ的中点在直线FP上，求△AQP的面积；（3）设t=8，是否存在以FP、FQ为邻边的矩形FPEQ，使得点E在Γ上？若存在，求点P的坐标；若不存在，说明理由．21.给定无穷数列{a n}，若无穷数列{b n}满足：对任意n∈N*，都有|b n-a n|≤1，则称{b n}与{a n}“接近”．（1）设{a n}是首项为1b n=a n+1+1，n∈N*，判断数列{b n}是否与{a n}接近，并说明理由；（2）设数列{a n}的前四项为：a1=1，a2=2，a3=4，a4=8，{b n}是一个与{a n}接近的数列，记集合M={x|x=b i，i=1，2，3，4}，求M中元素的个数m；（3）已知{a n}是公差为d的等差数列，若存在数列{b n}满足：{b n}与{a n}接近，且在b2-b1，b3-b2，…，b201-b200中至少有100个为正数，求d的取值范围．2018年普通高等学校招生全国统一考试（上海卷）数学答案和解析1. C2. A3. D4. B5. 186. y=±7. 218. 79. 510. 1411. -112. -314. 3617. 解：（1）∵圆锥的顶点为P，底面圆心为O，半径为2，圆锥的母线长为4，∴圆锥的体积V（2）∵PO=4，OA，OB是底面半径，且∠AOB=90°，M为线段AB的中点，∴以O为原点，OA为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，P（0，0，4），A（2，0，0），B（0，2，0），M（1，1，0），O（0，0，0），（1，1，-4（0，2，0），设异面直线PM与OB所成的角为θ，则∴θ=arccos．∴异面直线PM与OB所成的角的为18. 解：（1）∵f（x）=a sin2x+2cos2x，∴f（-x）=-a sin2x+2cos2x，∵f（x）为偶函数，∴f（-x）=f（x），∴-a sin2x+2cos2x=a sin2x+2cos2x，∴2a sin2x=0，∴a=0；（2）∵f，∴a+2cos2=a，∴f（x）x+2cos2x x+cos2x+1=2sin（2x+1，∵f（x）∴2sin（2x∴sin（2x）∴2x+2kπ，或2x kπ，k∈Z，∴xπ+kπ，或xπ+kπ，k∈Z，∵x∈[-π，π]，∴x x19. 解：（1）由题意知，当30＜x＜100时，f（x）=2x＞40，即x2-65x+900＞0，解得x＜20或x＞45，∴x∈（45，100）时，公交群体的人均通勤时间少于自驾群体的人均通勤时间；（2）当0＜x≤30时，g（x）=30•x%+40（1-x%）当30＜x＜100时，g（x）=（2x）•x%+40（1-x%）+58；∴g（x）当0＜x＜32.5时，g（x）单调递减；当32.5＜x＜100时，g（x）单调递增；说明该地上班族S中有小于32.5%的人自驾时，人均通勤时间是递减的；有大于32.5%的人自驾时，人均通勤时间是递增的；当自驾人数为32.5%时，人均通勤时间最少．20. 1设B（t，），则|BF t+2，∴|BF|=t+2；方法二：由题意可知：设B（t），由抛物线的性质可知：|BF|=t t+2，∴|BF|=t+2；（2）F（2，0），|FQ|=2，t=3，则|FA|=1，∴|AQ∴Q（3OQ的中点D，Dk QF PF方程：y x-2），3x2-20x+12=0，解得：x=，x=6（舍去），∴△AQP的面积S××（3）存在，设P（y），E m），则k PF k FQ直线QF方程为y x-2），∴y Q8-2）=，Q（8，则E（），∴）2=8），解得：y2=∴存在以FP、FQ为邻边的矩形FPEQ，使得点E在Γ上，且P21. 解：（1）数列{b n}与{a n}接近．理由：{a n}是首项为1可得a n b n=a n+1，则|b n-a n|=|+1-＜1，n∈N*，可得数列{b n}与{a n}接近；（2）{b n}是一个与{a n}接近的数列，可得a n-1≤b n≤a n+1，数列{a n}的前四项为：a1=1，a2=2，a3=4，a4=8，可得b1∈[0，2]，b2∈[1，3]，b3∈[3，5]，b4∈[7，9]，可能b1与b2相等，b2与b3相等，但b1与b3不相等，b4与b3不相等，集合M={x|x=b i，i=1，2，3，4}，M中元素的个数m=3或4；（3）{a n}是公差为d的等差数列，若存在数列{b n}满足：{b n}与{a n}接近，可得a n=a1+（n-1）d，①若d＞0，取b n=a n，可得b n+1-b n=a n+1-a n=d＞0，则b2-b1，b3-b2，…，b201-b200中有200个正数，符合题意；②若d=0，取b n=a1|b n-a n|=|a1a11，n∈N*，可得b n+1-b n0，则b2-b1，b3-b2，…，b201-b200中有200个正数，符合题意；③若-2＜d＜0，可令b2n-1=a2n-1-1，b2n=a2n+1，则b2n-b2n-1=a2n+1-（a2n-1-1）=2+d＞0，则b2-b1，b3-b2，…，b201-b200中恰有100个正数，符合题意；④若d≤-2，若存在数列{b n}满足：{b n}与{a n}接近，即为a n-1≤b n≤a n+1，a n+1-1≤b n+1≤a n+1+1，可得b n+1-b n≤a n+1+1-（a n-1）=2+d≤0，b2-b1，b3-b2，…，b201-b200中无正数，不符合题意．综上可得，d的范围是（-2，+∞）．【解析】1. 的焦点坐标在x轴，aP=1上的动点，由椭圆的定义可知：则P到该椭圆的两个焦点的距离之和为2a．故选：C．判断椭圆长轴（焦点坐标）所在的轴，求出a，直接利用椭圆的定义，转化求解即可．本题考查椭圆的简单性质的应用，椭圆的定义的应用，是基本知识的考查．2. 解：a∈R，则“a＞1”⇒⇒“a＞1或a＜0”，∴“a＞1故选：A．“a＞1”⇒⇒“a＞1或a＜0”，由此能求出结果．本题考查充分条件、必要条件的判断，考查不等式的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．3. 【解答】解：根据正六边形的性质，则D1-A1ABB1，D1-A1AFF1满足题意，而C1，E1，C，D，E，和D1一样，有2×4=8，当A1ACC1为底面矩形，有4个满足题意，当A1AEE1为底面矩形，有4个满足题意，故有8+4+4=16故选：D．【分析】根据新定义和正六边形的性质可得答案．本题考查了新定义，以及排除组合的问题，考查了棱柱的特征，属于中档题．4. 解：由题意得到：问题相当于圆上由12位后与下一个点会重合．我们可以通过代入和赋值的方法当f（1）0时，0，然而此时x=0或者x=1时，都有2个y与之对应，而我们知道函数的定义就是要求一个x只能对应一个y，因此只有当x此时满足一个x只会对应一个y，因此答案就选：B．故选：B．直接利用定义函数的应用求出结果．本题考查的知识要点：定义性函数的应用．5. 5-2×1=18．故答案为：18．直接利用行列式的定义，计算求解即可．本题考查行列式的定义，运算法则的应用，是基本知识的考查．6. 解：∵a=2，b=1，焦点在x轴上的渐近线方程为y=±∴的渐近线方程为y=±故答案为：y=±先确定双曲线的焦点所在坐标轴，再确定双曲线的实轴长和虚轴长，最后确定双曲线的渐近线方程．本题考察了双曲线的标准方程，双曲线的几何意义，特别是双曲线的渐近线方程，解题时要注意先定位，再定量的解题思想7. 解：二项式（1+x）7展开式的通项公式为T r+1x r，令r=2，得展开式中x2．故答案为：21．利用二项式展开式的通项公式求得展开式中x2的系数．本题考查了二项展开式的通项公式的应用问题，是基础题．8. 解：∵常数a∈R，函数f（x）=1og2（x+a）．f（x）的反函数的图象经过点（3，1），∴函数f（x）=1og2（x+a）的图象经过点（1，3），∴log2（1+a）=3，解得a=7．故答案为：7．由反函数的性质得函数f（x）=1og2（x+a）的图象经过点（1，3），由此能求出a．本题考查实数值的求法，考查函数的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．9. 【分析】本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题．把已知等式变形，然后利用复数代数形式的乘除运算化简，再由复数求模公式计算得答案.【解答】解：由（1+i）z=1-7i，则|z|=.故答案为5.10. 解：∵等差数列{a n}的前n项和为S n，a3=0，a6+a7=14，解得a1=-4，d=2，∴S7=7a1．故答案为：14．利用等差数列通项公式列出方程组，求出a1=-4，d=2，由此能求出S7．本题考查等差数列的前7项和的求法，考查等差数列的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．11. 解：∵α∈{-2，-1，1，2，3}，幂函数f（x）=xα为奇函数，且在（0，+∞）上递减，∴a是奇数，且a＜0，∴a=-1．故答案为：-1．由幂函数f（x）=xα为奇函数，且在（0，+∞）上递减，得到a是奇数，且a＜0，由此能求出a的值．本题考查实数值的求法，考查幂函数的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．12. 解：根据题意，设E（0，a），F（0，b）；∴a=b+2，或a=b-2；；当a=b+2∵b2+2b-2的最小值为；当a=b-2，最小值也为-3,-3.故答案为：-3．据题意可设E（0，a），F（0，b），从而得出|a-b|=2，即a=b+2，或a=b-2，并可求得a=b+2a=b-2带入，考查根据点的坐标求两点间的距离，根据点的坐标求向量的坐标，以及向量坐标的数量积运算，二次函数求最值的公式．13. 【分析】本题考查古典概型的概率的求法，是基本知识的考查．【解答】解：编号互不相同的五个砝码，其中5克、3克、1克砝码各一个，2克砝码两个，从中随机选取三个，3个数中含有1个2, 2个2，没有2，3种情况，，这三个砝码的总质量为9克的事件只有：5，3，1或5，2，2两个，所以：这三个砝码的总质量为914.解：等比数列{a n}的通项公式为q n-1（n∈N*），可得a1=1，1，，a n+1=q n．可得q=3．故答案为：3．利用等比数列的通项公式求出首项，通过数列的极限，列出方程，求解公比即可．本题考查数列的极限的运算法则的应用，等比数列求和以及等比数列的简单性质的应用，是基本知识的考查．15. 解：函数f（x）P（p Q（q整理得：，解得：2p+q=a2pq，由于：2p+q=36pq，所以：a2=36，由于a＞0，故：a=6．故答案为：6直接利用函数的关系式，利用恒等变换求出相应的a值．本题考查的知识要点：函数的性质的应用，代数式的变换问题的应用．16. 解：设A（x1，y1），B（x2，y2），（x1，y1（x2，y2），由x12+y12=1，x22+y22=1，x1x2+y1y2可得A，B两点在圆x2+y2=1上，1×cos∠AOB即有∠AOB=60°，即三角形OAB为等边三角形，AB=1，A，B两点到直线x+y-1=0的距离d1与d2之和，显然A，B在第三象限，AB所在直线与直线x+y=1平行，可设AB：x+y+t=0，（t＞0），由圆心O到直线AB的距离d可得，解得t即有两平行线的距离为的最大值为故答案为：+．设A（x1，y1），B（x2，y2（x1，y1），（x2，y2），由圆的方程和向量数量积的定义、坐标表示，可得三角形OAB为等边三角形，AB=1何意义为点A，B两点到直线x+y-1=0的距离d1与d2之和，由两平行线的距离可得所求最大值．本题考查向量数量积的坐标表示和定义，以及圆的方程和运用，考查点与圆的位置关系，运用点到直线的距离公式是解题的关键，属于难题．17. （1）由圆锥的顶点为P，底面圆心为O，半径为2，圆锥的母线长为4能求出圆锥的体积．（2）以O为原点，OA为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，利用向量法能求出异面直线PM与OB所成的角．本题考查圆锥的体积的求法，考查异面直线所成角的正切值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．18. 本题考查了三角函数的化简和求值，以及三角函数的性质，属于基础题．（1）根据函数的奇偶性和三角函数的性质即可求出，（2）先求出a的值，再根据三角形函数的性质即可求出．19. 本题考查了分段函数的应用问题，也考查了分类讨论与分析问题、解决问题的能力．（1）由题意知求出f（x）＞40时x的取值范围即可；（2）分段求出g（x）的解析式，判断g（x）的单调性，再说明其实际意义．20. （1）方法一：设B点坐标，根据两点之间的距离公式，即可求得|BF|；方法二：根据抛物线的定义，即可求得|BF|；（2）根据抛物线的性质，求得Q点坐标，即可求得OD的中点坐标，即可求得直线PF 的方程，代入抛物线方程，即可求得P点坐标，即可求得△AQP的面积；（3）设P及E点坐标，根据直线k PF•k FQ=-1，求得直线QF的方程，求得Q点坐标，E2=8），即可求得P点坐标．本题考查抛物线的性质，直线与抛物线的位置关系，考查转化思想，计算能力，属于中档题．21. （1）运用等比数列的通项公式和新定义“接近”，即可判断；（2）由新定义可得a n-1≤b n≤a n+1，求得b i，i=1，2，3，4的范围，即可得到所求个数；（3）运用等差数列的通项公式可得a n，讨论公差d＞0，d=0，-2＜d＜0，d≤-2，结合新定义“接近”，推理和运算，即可得到所求范围．本题考查新定义“接近”的理解和运用，考查等差数列和等比数列的定义和通项公式的运用，考查分类讨论思想方法，以及运算能力和推理能力，属于难题．第11页，共11页。

2018年普通高等学校招生全国统一考试(上海卷) 数 学 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、填空题（本大题共有12题，满分54分第1-6题每题4分，第7-12题每题5分） 1.行列式4125的值为 。

2.双曲线2214x y -=的渐近线方程为 。

3.在（1+x ）7的二项展开式中，x ²项的系数为 。

（结果用数值表示） 4.设常数a R ∈，函数f x x a =+（）㏒₂（），若f x （）的反函数的图像经过点31（，），则a= 。

5.已知复数z 满足117i z i +=-（）（i 是虚数单位），则∣z ∣= 。

6.记等差数列{} n a 的前几项和为S n ，若87014a a a =+=₃，，则S 7= 。

7.已知21123α∈---｛，，，，，，｝，若幂函数()n f x x =为奇函数，且在0+∞（，）上速减，则α=_____8.在平面直角坐标系中，已知点A （-1，0），B （2，0），E ，F 是y 轴上的两个动点，且|EF |=2，则AE ·BF 的最小值为______ 9.有编号互不相同的五个砝码，其中5克、3克、1克砝码各一个，2克砝码两个，从中随机选取三个，则这三个砝码的总质量为9克的概率是______（结果用最简分数表示） 10.设等比数列{错误!未找到引用源。

}的通项公式为a n =q ⁿ+1（n ∈N*），前n 项和为S n 。

若1Sn 1lim 2n n a →∞+=，则q=____________ 11.已知常数a >0，函数222()(2)f x ax =+的图像经过点65p p ⎛⎫ ⎪⎝⎭，、15Q q ⎛⎫- ⎪⎝⎭，，若236p q pq +=，则a =__________ 12.已知实数x ₁、x ₂、y ₁、y ₂满足：²²1x y +=₁₁，²²1x y +=₂₂，212x x y y +=₁₂₁，则2+2的最大值为__________ 二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确选项.考生应在答题纸的相应位置，将代表正确选项的小方格涂黑. 13.设P 是椭圆 ²5x + ²3y =1上的动点，则P 到该椭圆的两个焦点的距离之和为（ ） （A ）2错误!未找到引用源。

2018年普通高等学校招生全国统一考试（上海卷）数学试卷（满分150分,考试时间120分钟）考生注意1.本场考试时间120分钟,试卷共4页,满分150分,答题纸共2页.2.作答前,在答题纸正面填写姓名,准考证号,反面填写姓名,将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题,用黑色字迹钢笔,水笔或圆珠笔作答非选择题.一,填空题（本大题共有12题,满分54分,第1～6题每题4分,第7～12题每题5分）1.行列式4125的值为_________.2.双曲线2214x y -=的渐近线方程为_________. 3.在7(1)x +的二项展开式中,2x 项的系数为_________.（结果用数值表示） 4.设常数a R ∈,函数2()log ()f x x a =+。

若()f x 的反函数的图像经过点(3,1),则a =_________.5.已知复数z 满足(1)17i z i +=-（i 是虚数单位）,则z =_________.6.记等差数列{}n a 的前n 项和为n S ,若30a =,6714a a +=,则7S =_________.7.已知12,1,,1,2,32α⎧⎫∈---⎨⎬⎩⎭。

若幂函数()f x x α=为奇函数,且在(0,)+∞上递减,则 α=_________.8.在平面直角坐标系中,已知点(1,0)A -,(2,0)B ,E ,F 是y 轴上的两个动点,且2EF =,则AE BF •的最小值为_________.9.有编号互不相同的五个砝码,其中5克,3克,1克砝码各一个,2克砝码两个。

从中随机选取三个,则这三个砝码的总质量为9克的概率是_________.（结果用最简分数表示）10.设等比数列{}n a 的通项公式为1n n a q-=（*n ∈N ）,前n 项和为n S 。

C9k x9k
a2k x2k
C9k ak x93k ,k
3,
常数项为C93a3 a 4
10．设 m R ，若 z 是关于 x 的方程 x2 mx m2 1 0 的一个虚根，则 | z | 的取值范围
是__________．
答案：（ 3 ，+） 3
解析：
法一：设z a bi,(b 0)代入方程得：（a bi）2 +m(a bi) m2 1 0,即 a2 b2 ma m2 1 0, 2ab mb 0
（B）60
（C）81
（D）108
本题考查向量的投影，因为 AP 5,所以P点在以A为圆心半径为5的圆面上， 又AP AB 6= AB AP cos ,所以 AP cos =3,根据题意作图如下：
三、解答题（本大题共有 5 题，满分 76 分，第 17~19 题每题 14 分，20 题 16 分， 21 题 18 分）
3/7
仅供学习交流、勿做商用！
答案：A
14．如图，在直三棱柱 ABC A1B1C1 的棱虽在的直线中，与直线 BC1
异面的直线条数为（ ）
（A）1
（B）2
（C）3
（D）4
答案：C
15．记 Sn 为数列{an}的前 n 项和．“{an}是递增数列”是“ Sn 为递增数列”的（ ）
（A）充分非必要条件
答案： C31C53P33 180
9．设 a R
，若

x2

2 x
9

与

x

a x2
9

的二项展开式中的常数项相等，则 a

【试题级别】高三
【试题地区】上海
【试题来源】2018年高考数学真题试卷（上海卷）
15.（2018•上海）《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA₁是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以AA₁为底面矩形的一边，则这样的阳马的个数是（）
A.4
B.8
C.12
D.16
【答案】D
【解析】【解答】以AA1取矩形分别讨论，找到AA1所在矩形个数，并根据每个矩形可做4个阳马的基本位置关系，可得答案为D。

故答案为：D。

【分析】以AA1为底边的直四棱锥，运用线面垂直关系判定的方法分析图形中基本元素及其相互关系解答即可。

【题型】单选题
【考查类型】高考真题
【试题来源】2018年高考数学真题试卷（上海卷）。

（C） 3 3
（D）0【答案】 B
【知识点】函数的概念【考查能力】空间想象能力
【解析】点 (1, f (1)) 在直线 x = 1 上，把直线进行旋转可得旋转后的直线，这样进
行下去直到回到 (1, f (1)) 点可知 f (1) = 3 2
17. 已知圆锥的顶点为 P ，底面圆心为 O ，半径为 2，
2
2
【知识点】直线的交点坐标与距离公式
【解析】数形结合，转化单位圆上圆心角为 60o的两点到直线 x + y -1 = 0 的距离
之和，可求得最大值为 2 + 3 。
13. 设 P 是椭圆 x2 + y2 = 1 上的动点，则 P 到该椭圆的两个焦点的距离之和为（
）．
53
（A） 2 2
（B） 2 3
O
B
A
M
（2）若
f
æ çè
p 4
ö ÷ø
=
3 +1，求方程 f ( x) = 1-
2 在区间[-p ,p ] 上的解．
1）、由偶函数可知 f (-x) = f (x) 得 a = 0 。
（2）、 f (p ) = 3 +1Þ a = 3 ， f (x) = 2sin(2x + p ) +1, \sin(2x + p ) = - 2 ，在
（C） 2 5
（D） 4 2 【答案】 C
14. 已知 a Î R ，则“ a > 1”是“ 1 < 1 ”的（
）．
a
（A）充分非必要条件 （B）必要非充分条件
（C）充要条件 （D）既非充分又非必要条件【答案】 A
15. 《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马．设 AA1 是正六 棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以 AA1 为底面矩形的一边，

A.4 B.8 C.12 D.16 解析：根据正六边形的性质，则 D1﹣A1ABB1，D1﹣A1AFF1 满足题意，而 C1，E1，C，D，E，和 D1 一样，有 2×6=12， 当 A1ACC1 为底面矩形，有 2 个满足题意， 当 A1AEE1 为底面矩形，有 2 个满足题意， 故有 12+2+2=16

6

3 . 2
解析：(1)由圆锥的顶点为 P，底面圆心为 O，半径为 2，圆锥的母线长为 4 能求出圆锥的体 积. (2)以 O 为原点，OA 为 x 轴，OB 为 y 轴，OP 为 z 轴，建立空间直角坐标系，利用向量法能 求出异面直线 PM 与 OB 所成的角. 答案：(1)∵圆锥的顶点为 P，底面圆心为 O，半径为 2，圆锥的母线长为 4，
)+1， 6


6

2
∵b +2b﹣2 的最小值为
2
8 4 3 ； 4
∴ A E B F 的最小值为﹣3，同理求出 b=a+2 时， A E B F 的最小值为﹣3. 答案：﹣3 9.有编号互不相同的五个砝码，其中 5 克、3 克、1 克砝码各一个，2 克砝码两个，从中随 机选取三个，则这三个砝码的总质量为 9 克的概率是____(结果用最简分数表示). 解析：编号互不相同的五个砝码，其中 5 克、3 克、1 克砝码各一个，2 克砝码两个， 从中随机选取三个，3 个数中含有 1 个 2；2 个 2，没有 2，3 种情况， 所有的事件总数为： C 53 =10， 这三个砝码的总质量为 9 克的事件只有：5，3，1 或 5，2，2 两个， 2 1 所以：这三个砝码的总质量为 9 克的概率是： . 10 5 1 答案： 5 10.设等比数列{an}的通项公式为 an=q

2018年普通高等学校招生全国统一考试上海 数学试卷一、填空题（本大题共有12题，满分54分第1-6题每题4分，第7-12题每题5分）1.行列式4125的值为 。

2.双曲线2214x y -=的渐近线方程为 。

3.在（1+x ）7的二项展开式中，x ²项的系数为 。

（结果用数值表示）4.设常数a R ∈，函数f x x a =+（）㏒₂（），若f x （）的反函数的图像经过点31（，），则a= 。

5.已知复数z 满足117i z i +=-（）（i 是虚数单位），则∣z ∣= 。

6.记等差数列{} n a 的前几项和为S n ，若87014a a a =+=₃，，则S 7= 。

7.已知21123α∈---｛，，，，，，｝，若幂函数()n f x x =为奇函数，且在0+∞（，）上速减，则α=_____8.在平面直角坐标系中，已知点A （-1，0），B （2，0），E ，F 是y 轴上的两个动点，且|EF |=2，则AE ·BF 的最小值为______9.有编号互不相同的五个砝码，其中5克、3克、1克砝码各一个，2克砝码两个，从中随机选取三个，则这三个砝码的总质量为9克的概率是______（结果用最简分数表示）10.设等比数列{a n }的通项公式为a n =q ⁿ+1（n ∈N *），前n 项和为S n 。

若1Sn 1lim2n n a →∞+=，则q=____________11.已知常数a >0，函数222()(2)f x ax =+的图像经过点65p p ⎛⎫⎪⎝⎭，、15Q q ⎛⎫- ⎪⎝⎭，，若236p q pq +=，则a=__________12.已知实数x ₁、x ₂、y ₁、y ₂满足：²²1x y +=₁₁，²²1x y +=₂₂，212x x y y +=₁₂₁，则的最大值为__________二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确选项.考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.13.设P 是椭圆 ²5x +²3y =1上的动点，则P 到该椭圆的两个焦点的距离之和为（ ）（A ）2√2 （B ）2√3 （C ）2√5 （D ）4√214.已知a R ∈，则“1a ﹥”是“1a1﹤”的（ ）（A ）充分非必要条件 （B ）必要非充分条件（C）充要条件（D）既非充分又非必要条件15.《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA₁是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以AA₁为底面矩形的一边，则这样的阳马的个数是（）（A）4 （B）8（C）12 （D）1616.设D是含数1的有限实数集，f x（）是定义在D上的函数，若f x（）的图像绕原点逆时针旋转π6后与原图像重合，则在以下各项中，1f（）的可能取值只能是（）（A）3（B）3（C）3（D）0三、解答题（本大题共有5题，满分76分）解答下列各题必须在答题纸的相应位置写出必要的步骤.17.（本题满分14分，第1小题满分6分，第2小题满分8分）已知圆锥的顶点为P，底面圆心为O，半径为2（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA，OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图，求异面直线PM与OB所成的角的大小.18.（本题满分14分，第1小题满分6分，第2小题满分8分）设常数a R ∈，函数f x （）22?asin x cos x =+ （1）若f x （）为偶函数，求a 的值； （2）若4f π〔〕1=，求方程1f x =（）ππ-［，］上的解。

2018年上海市春季高考数学试卷2018.1一.填空题（本大题共12题，满分54分，第1~6题每题4分，第7~12题每题5分）1、不等式1>x 的解集为______________；2、计算：_________213lim=+-∞→n n n ；3、设集合{}20<<=x x A ，{}11<<-=x x B ，则________=B A ；4、若复数i z +=1（i 是虚数单位），则______2=+zz ；5、已知{}n a 是等差数列，若1082=+a a ，则______753=++a a a ；6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4，则动点P 的轨迹方程为_________；7、如图，在长方体1111D C B A ABCD -中，3=AB ，4=BC ，51=AA ，O 是11C A 的中点，则三棱锥11OB A A -的体积为_________；8、某校组队参加辩论赛，从6名学生中选出4人分别担任一、二、三、四辩，若其中学生甲必须参赛且不担任四辩，则不同的安排方法种数为_____________（结果用数值表示）。

9、设R a ∈，若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等，则_______=a ；10、设R m ∈，若z 是关于x 的方程0122=-++m mx x 的一个虚根，则-z 的取值范围是________；11、设0>a ，函数()()1,0),sin()1(2∈-+=x ax x x x f ，若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点，则a 的取值范围是__________；12、如图，在正方形ABCD 的边长为20米，圆O 的半径为1米，圆心是正方形的中心，点P 、Q 分别在线段AD 、CB 上，若线段PQ 与圆O 有公共点，则称点Q 在点P 的“盲区”中，已知点P以1.5米/秒的速度从A 出发向D 移动，同时，点Q 以1米/秒的速度从C 出发向B 移动，则在点P 从A 移动到D 的过程中，点Q 在点P 的盲区中的时长均为_____秒（精确到0.1）.二.选择题（本大题共4题，每题5分，共20分）13、下列函数中，为偶函数的是（）A2-=xy B31xy =C 21-=xy D 3xy =14、如图，在直三棱柱111C B A ABC -的棱所在的直线中，与直线1BC 异面的直线的条数为（）A1B2C 3D415、若数列}{n a 的前n 项和，“}{n a 是递增数列”是“}{n S 是递增数列”的（）A 充分不必要条件B 必要不充分条件C 充要条件D 即不充分也不必要条件16、已知A 、B 是平面内两个定点，且2=→AB ，该平面上的动线段PQ 的两个端点P 、Q满足：5≤→AP ，6=⋅→→AB AP ，→→-=AP AQ 2，则动线段PQ 所围成的面积为（）A、50B、60C、72D、108三.解答题（本大题共5题，共14+14+14+16+18=76分）17、已知x x f cos )(=（1）若31)(=αf ，且],0[πα∈，求)3(πα-f 的值；（2）求函数)(2)2(x f x f y -=的最小值；18、已知R a ∈，双曲线1:222=-Γy ax （1）若点)1,2(在Γ上，求Γ的焦点坐标；（2）若1=a ，直线1+=kx y 与Γ相交于B A ,两点，若线段AB 中点的横坐标为1，求k 的值；19、利用“平行与圆锥母线的平面截圆锥面，所得截线是抛物线”的几何原理；某公司用两个射灯（射出的光锥视为圆锥）在广告牌上投影出其标识，如图1所示，图2投影出的抛物线的平面图，图3是一个射灯投影的直观图，在图2与图3中，点O 、A 、B 在抛物线上，OC 是抛物线的对称轴，AB OC ⊥于C ，3=AB 米，5.4=OC 米.（1）求抛物线的焦点到准线的距离；（2）在图3中，已知OC 平行于圆锥的母线SD ，AB 、DE 是圆锥底面的直径，求圆锥的母线与轴的夹角的大小（精确到01.0）.20、设0>a ，函数xa x f 211)(⋅+=（1）.若1=a ，求)(x f 的反函数)(1x f -（2）求函数)()(x f x f y -⋅=的最大值，（用a 表示）（3）设=)(x g )1()(--x f x f ，若对任意)0()(],0,(g x g x ≥-∞∈恒成立，求a 的取值范围？21、若}{n c 是递增数列，数列}{n a 满足：对任意*,N m R n ∈∃∈，使得01≤--+n m nm c a a a ，则称}{n a 是}{n c 的“分隔数列”（1）设1,2+==n a n c n n ，证明：数列}{n a 是}{n c 的分隔数列；（2）设n n S n c ,4-=是}{n c 的前n 项和，23-=n n c d ，判断数列}{n S 是否是数列}{n d 的分隔数列，并说明理由；（3）设n n n T aq c ,1-=是}{n c 的前n 项和，若数列}{n T 是}{n C 的分隔数列，求实数q a ,的取值范围？2018年春考——参考答案一、填空题：1、()()+∞-∞-,11, ；2、3；3、()1,0；4、2；5、15；6、13422=+y x ；7、5；8、180；9、4；10、⎪⎪⎭⎫ ⎝⎛∞+33；11、⎦⎤⎝⎛619611ππ，；12、4.4；二、选择题：13、A ；14、C ；15、D ；16、B ；三、解答题：17、（1）6621+；（2）23-；18、（1）()()0,30,3-，；（2）215-；19、（1）41；（2）59.9；20、（1）()()1,011log )(21∈⎪⎭⎫⎝⎛-=-x x x f；（2）()211+a ；（3）(；21、（1）证明-略；（2）数列{}n S 不是数列{}n d 的分隔数列；（3）0>a 或2≥q ；。

2018年上海市普通高等学校春季招生统一文化考试数学试卷一、填空题（本大题共有12题，满分54分，第1~6题每题4分，第7~12题每题5分）1．不等式||1x >的解集为__________． 2．计算：31lim 2n n n →∞-=+__________．3．设集合{|02}A x x =<<，{|11}B x x =-<<，则A B =__________．4．若复数z i i =+（i 是虚数单位），则2z z+=__________． 5．已知{}n a 是等差数列，若2810a a +=，则357a a a ++=__________．6．已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4，则动点P 的轨迹为__________．7．如图，在长方形1111B ABC A C D D -中，3AB =，4BC =，15AA =， O 是11A C 的中点，则三棱锥11A AOB -的体积为__________．第7题图 第12题图 8．某校组队参加辩论赛，从6名学生中选出4人分别担任一、二、三、 四辩．若其中学生 甲必须参赛且不担任四辩，则不同的安排方法种数为__________．9．设a R ∈，若922x x ⎛⎫+ ⎪⎝⎭与92a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等，则a =__________．10．设m R ∈，若z 是关于x 的方程2210xmx m -+=+的一个虚根，则||z 的取值范围是__________．11．设0a >，函数()2(1)sin()f x x x ax =+-，(0,1)x ∈，若函数21y x =-与()y f x =的图象有且仅有两个不同的公共点，则a 的取值范围是__________．12．如图，正方形ABCD 的边长为20米，圆O 的半径为1米，圆心是正方形的中心，点P 、Q 分别在线段AD 、CB 上，若线段PQ 与圆O 有公共点，则称点Q 在点P 的“盲区”中．已知点P 以1．5米/秒的速度从A 出发向D 移动，同时，点Q 以1米/秒的速度 从C 出发向B 移动，则在点P 从A 移动到D 的过程中，点Q 在点P 的盲区中的时长约为__________秒（精确到0．1）二、选择题（本大题共有4题，满分20分，每题5分）13．下列函数中，为偶函数的是（ ） （A ）2y x-= （B ）13y x =（C ）12y x-=（D ）3y x =14．如图，在直三棱柱111AB A B C C -的棱虽在的直线中，与直线1BC异面的直线条数为（ ） （A ）1 （B ）2（C ）3（D ）415．记n S 为数列{}n a 的前n 项和．“{}n a 是递增数列”是“n S 为递增数列”的（ ） （A ）充分非必要条件 （B ）必要非充分条件（C ）充要条件（D ）既非充分也非必要条件16．已知A 、B 为平面上的两个定点，且|2|AB =．该平面上的动线段PQ 的端点P 、Q ，满足||5AP ≤，6AB AP ⋅=，2AQ AP =-，则动线段PQ 所形成图形的面积为（ ）（A ）36（B ）60（C ）81（D ）108三、解答题（本大题共有5题，满分76分，第17~19题每题14分，20题16分，21题18分）17．（本题满分14分，第1小题满分6分，第2小题满分8分） 已知cos y x =．（1）若3(1)f α=，且[0,]απ∈，求()3f πα-的值；（2）求函数(2)2()y f x f x =-的最小值．18． （本题满分14分，第1小题满分6分，第2小题满分8分）已知a R ∈，双曲线222:1x y aΓ-=．（1）若点(2,1)在Γ上，求Γ的焦点坐标；（2）若1a =，直线1y kx =+与Γ相交于A 、B 两点，且线段AB 中点的横坐标为1，求实数k 的值．19．（本题满分14分，第1小题满分7分，第2小题满分7分）利用“平行于圆锥曲线的母线截圆锥面，所得截线是抛物线”的几何原理，某快餐店用两个射灯（射出的光锥视为圆锥）在广告牌上投影出其标识，如图1所示，图2是投影出的抛物线的平面图，图3是一个射灯的直观图，在图2与图3中，点O 、A 、B 在抛物线上，OC 是抛物线的对称轴，OC AB ⊥于C ，3AB =米， 4.5OC =米．（1）求抛物线的焦点到准线的距离；（2）在图3中，已知OC 平行于圆锥的母线SD ，AB 、DE 是圆锥底面的直径，求圆锥的母线与轴的夹角的大小（精确到0．01°）．图1 图2 图3 20．（本题满分16分，第1小题满分4分，第2小题满分6分，第3小题满分6分） 设0a>，函数1()12xf x a =+⋅．（1）若1a =，求()f x 的反函数1()f x -；（2）求函数()()y f x f x ⋅-=的最大值（用a 表示）；（3）设()()(1)g x f x f x =--．若对任意(,0]x ∈-∞，)(()0g x g ≥恒成立，求a 的取值范围．21．（本题满分18分，第1小题满分3分，第2小题满分6分，第3小题满分9分）若{}n c 是递增数列，数列{}n a 满足：对任意*n N ∈，存在*m N ∈，使得10m nm n a c a c +-≤-，则称{}n a 是{}n c 的“分隔数列”．（1）设2n c n =，1n a n =+，证明：数列{}n a 是{}n c 的“分隔数列”；（2）设4nc n =-，n S 是{}n c 的前n 项和，31n nd c -=，判断数列{}n S 是否是数列{}n d 的分隔数列，并说明理由；（3）设1n nc aq -=，n T {}n c 的前n 项和，若数列{}n T 是{}n c 的分隔数列，求实数a 、q 的取值范围．参考答案一、填空题1．(,1)(1,)-∞-+∞2．33．(0,1)4．25．156．22143x y +=7．5 8．180 9．410．)+∞ 11．1119(,]66ππ12．4.4二、选择题13．A14．C15．D16．B三、解答题17．（1）16+；（2）32-18．（1）)(；（2． 19．（1）14；（2）9.59︒． 20．（1）121()log (01)x f x x x --=<<；（2）2112max y a a =++（0x =时取最值）；（3）21．（1）证明略；（2）不是．反例：4n=时，m 无解；（3）02a q ≥>⎧⎨⎩．参考答案一、填空题1．(,1)(1,)-∞-+∞2．33．(0,1)4．25．156．22143x y +=7．5 8．180 9．410．)+∞ 11．1119(,]66ππ提示：1212(1)sin()12(1)sin()sin()2x x x ax x x ax ax --=-⇒-=-⇒=-711711711,,2,2,4,4,666666ax ππππππππππ∴=++++0ax a << 117266a πππ∴<≤+ 12．4.4 提示：以A 为原点建立坐标系，设时刻为t ，则40(0,1.5),(20,20),03P t Q t t -≤≤则0 1.5:20020 1.5PQx y tl t t--=---，化简得(8)8120t x y t --+= 点(10,10)O 到直线PQ1≤，化简得23161280t t +-≤即8833t ---+≤≤880 4.433t t -+-+≤≤⇒∆=≈ 二、选择题13．A14．C15．D16．B 提示：建系(0,0),(2,0)A B ，则(,)P x y 的轨迹为线段3,44x y =-≤≤，AP 扫过的三角形面积为12，则利用相似三角形可知AQ 扫过的面积为48，因此和为60三、解答题17．（1；（2）32-18．（1）(；（2． 19．（1）14；（2）9.59︒． 20．（1）121()log (01)x f x x x --=<<；（2）2112max y a a =++（0x =时取最值）； （3）提示：1211()21212232x x x xa g x a a a a --=-=+⋅+⋅⋅++2,(2(0,1])23x at a t at-=∈⋅++ 因为-a <0，所以当x =0,t =1时，分母取到最小值从而分式值取到最小值，此时2210a t t a t =⇒=≥⇒<≤21．（1）证明：存在2m n =,此时*1,22122n m n n c n a n c n +∀∈=<=+<=+N 证毕 （2）不是．反例：4n=时，m 无解；（3）02a q ≥>⎧⎨⎩．提示：因为1{}n aq -为递增数列，因此01a q >⎧⎨>⎩或者001a q <⎧⎨<<⎩①当001a q <⎧⎨<<⎩时，*,0n n c ∈<N ，因此321123T T T c c c <<<=<<<因此不存在23m c T c ≤<，不合题意。

2018-2020年上海四校自招数学试卷汇编版（含答案）--共9套目录2018交附自招数学答案2018上中自招数学2018上中自招数学答案2019复附自招数学答案2019交附自招数学2020上中、交附、七宝自招上海中学自招试题上海中学自招真题解析2018上海市上海中学自招部分真题1、因式分解：6x3-11x2+x+4=【答案】(x-1)(3x-4)(2x+1)【解析】试根法易得x=1时，上式值为0.利用长除法可得原式=(x-1)(6x2-5x-4)=(x-1)(3x-4)(2x+1)2、设a>b>0，a2+b2=4ab，则a+b=a-b【答案】3【解析】令a+b=x，a-b=y则x>y>0a2+b2=4aba2+b2-2ab=2aby2=1(x2-y2)2x2=3y2xa+b=3=3即y a-b3、若x2+x-1=0，则x3+2x2+3=【答案】4【解析】降次法x2=1-x所以原式=x(1-x)+2(1-x)+3=x-x2+2-2x+3=-x-(1-x)+5=4(,34、已知1(b -c )2=(a -b )(c -a )，且a ≠0，则b +c =4a【答案】2【解析】1(b -c )2=(a -b )(c -a )4(c -b )2=4(a -b )(c -a )⎡⎣(c -a )+(a -b )⎤⎦2=4(c -a )(a -b )⎡⎣(c -a )-(a -b )⎤⎦2=0所以c -a =a -bb +c =2a 即b +c=2a5、一个袋子里装有两个红球和一个白球（仅颜色不同），第一次从中取出一个球，记下颜色后放回，摇匀，第二次从中取出一个球，则两次都是红球的概率是【答案】49【解析】P =2⨯2=43396,、直线l ：y =-3x +与x 、y 轴交于点A 、B ，△AOB 关于直线AB 对称得到△ACB ，则点C 的坐标是【答案】33)22【解析】如右图所示易得∠CAD =∠BAO =60︒过C 作CD ⊥x 轴于点D 在△ACD 中AC =1易解得AD =1，CD =3223C (,)223即7、一张矩形纸片ABCD，AD=9，AB=12，将纸片折叠，使A、C两点重合，折痕的长是【答案】45 4【解析】如右图所示易得AC=所以OC=152=15△C△OF∽ABC所以OF=OC解得OF=45即EF=45 AB BC848、任给一个正整数n，如果n是偶数，就将它减半（即n），如果n是奇2数，则将它乘以3再加1（即3n+1），不断重复这样的运算，现在请你研究：如果对于正整数n（首项）按照上述规则实施变换（注：1可以多次出现）后的第八项为1，则n所有可能取值为【答案】128/2/16/20/3/21【解析】92+12212418 12451081632642 163 20 21 1289、正六边形ABCDEF 的面积是6平方厘米，联结AC 、CE 、EA 、BD 、DF 、FB ，求阴影部分小正六边形的面积【答案】2【解析】将小六边形的相对顶点联结后易得：小正六边形的面积是大正六边形面积的13即面积为210、已知y 1=2x 2+(4-m )x +(4-m )与y =mx 在x 取任意实数时，至少有一个是正数，则m 的取值范围为【答案】m <4【解析】（1）当0<m 时，0<x ，y 2=mx >0，且x ≤0时，y 2≤0∴x ≤0时y 1>0∴y 1x =0>0故4-m >0∴m -4<04则∆<0解得-4<m <4∴0<m <4（2）当m <0时，同理解得m <0（3）当m =0时，y 1>0恒成立综上所述，m <411、已知a 、b 、c 是互不相等的实数，x 是任意实数，(x -a )2(x -b )2(x -c )2化简：++=(a -b )(a -c )(c -b )(a -b )(c -a )(c -b )【答案】1-(x -a )2(b -c )-(x -b )2(c -a )-(x -c )2(a -b )=(a -b )(b -c )(c -a )【解析】原式=(a -b )(b -c )(c -a )(a -b )(b -c )(c -a )=1212、已知实数a 、b 满足a 2+ab +b 2=1，t =ab -a 2-b 2，-⎩1则t 的取值范围是【答案】-3≤t ≤-13【解析】由a 2+b 2≥2ab ，a 2+b 2≥-2ab得⎧1-ab ≥2ab 解得-1≤ab ≤1⎨ab ≥-2ab 3t =ab -(1-ab )=2ab -1所以-3≤t ≤-1313、（1）求边长是1的正五边形的对角线长（2）求sin18︒【答案】（1）5+1（2）5-122【解析】（1）正五边形的一个内角大小为：(5-2)⨯180︒÷5=108︒所以△ABE 和△ACD 是黄金三角形在△ABE 中AE =BE 5-1其中AE =1解得BE =25+12（2）在△ACD 中过A 作AF 垂直CD 于点F易得∠FAD =18︒1所以sin18︒=FD =2=5-1AD5+122x y -1⎩14、（1）f (x )=x 3+ax 2+bx +c ，0<f (-1)=f (-2)=f (-3)<3，求c 的取值范围（2）f (x )=x 4+ax 3+bx 2+cx +d ，f (1)=10，f (2)=20，f (3)=30，求f (10)+f (-6)【答案】（1）6<c ≤9（2）8104【解析】（1）令f (-1)=f (-2)=f (-3)=k ，g (x )=f (x )=k ，0<k ≤3则g (x )=(x +1)(x +2)(x +3)所以f (x )=g (x )+k =x 3+6x 2+11x +6+k 故c =6+k ，又0<k <3所以6<c ≤9（2）f (1)=10，f (2)=20，f (3)=30令g (x )=f (x )-10x =x 4+ax 3+bx 2+(c -10)x +d则有g (1)=g (2)=g (3)=0令g (x )=0的第四个根是m 则g (x )=(x -1)(x -2)(x -3)(x -m )所以g (10)+g (-6)=9⨯8⨯7⨯(10-m )+(-7)⨯(-8)⨯(-9)(-6-m )=8064即f (10)+f (-6)=g (10)+g (-6)+40=810415、我们学过直线与圆的位置关系，根据材料完成问题（1）（2）背景知识：平面α：Ax +By +Cz +d =0；球：(x -a )2+(y -b )2+(z -c )2=R 2；点(a ,b ,c )到平面α的距离公式：d =球心到平面的距离为d ，当d <R 时，球与平面相交，当d =R 时，球与平面相切，当d >R 时，球与平面相离；问题（1）：若实数m 、n 、k 满足m +n +k =1，求m 2+n 2+k 2的最小值；问题（2）：解方程++=1(x +y +z )2⎧x =1【答案】（1）1（2）⎪y =2⎨3⎪z =3【解析】（1）设点(m ,n ,k )则该点在平面x +y +z =1上而所求m 2+n 2+k 2即为该点到原点距离的平方Aa +Bb +Cc +D A 2+B 2+C 2z -212+12+12y -1z -2x y -1x ⎨⎨原点到平面x +y +z =1的距离为：d =1=33⎛3⎫21所以(m 2+n 2+k 2)= ⎪=（2）配方法min⎝3⎭3++=1(x +y +z )2x +y +z -(2+2+2z -2)=0(-1)2+(⎧x =1-1)2+(⎧x =1-1)2=0⎪y -1=1解得⎪y =2⎪⎪z =3⎪z -2=1⎩x y -1z -2则交大附中自主招生试卷2018.03第一部分 1. 已知13x x +=-，求3311000x x++. 2. 11(1)x x x tx x x x +++=++有增根，求所有可能的t 之和.3. AB ∥CD ，15AB =，10CD =，3AD =，4CB =，求ABCD S .4. 346y x x =-+，若a x b ≤≤时，其中x 的最小值为a ，最大值为b ，求a b +.5. 22(2)y x m =-+，若抛物线与x 轴交点与顶点组成正三角形，求m 的值.6. DE 为»BC的切线，正方形ABCD 边长为200，»BC 以BC 为直径的半圆，求DE 的长.7. 在直角坐标系中，正ABC ∆，(2,0)B ，9(,0)2C 过点O 作直线DMN ，OM MN =， 求M 的横坐标.8. 四圆相切⊙B 与⊙C 半径相同，⊙A 过⊙D 圆心，⊙A 的半径为9，求⊙B 的半径.9. 横纵坐标均为整数的点为整点，（12m a <<），y mx a =+（1100x ≤≤），不经过整 点，求a 可取到的最大值.10. G 为重心，DE 过重心，1ABC S ∆=，求ADE S ∆的最值，并证明结论.第二部分（科学素养）1. 已知直角三角形三边长为整数，有一条边长为85，求另两边长（写出10组）.2. 阅读材料，根据凸函数的定义和性质解三道小题，其中第（3）小题为不等式证明 1212[(1)]()1()f bx b x bf x bf x ++<+-（1）14b =；（2）13b =.（注：选（1）做对得10分，选（2）做对得20分）3. 请用最优美的语言赞美仰晖班（80字左右）（17分）4. 附加题（25分） （2 points ） solve the following system of equations for 2122.2221w x y z w x y z w w x y z w x y z +++=⎧⎪+++=⎪⎨+++=⎪⎪+++=⎩（4 points ）Compute 98∞（6 points ）Solve the equation 1=.Express your answer as a reduced fraction with the numerator written in their prime factorization.The gauss function []x denotes the greatest less than or equal to xA ）（3 points ）Compute 2018!2015!2017!2016!+⎡⎤⎢⎥+⎣⎦B ）（4points ）Let real numbers 12,,,n x x x ⋅⋅⋅ be the solutions of the equation 23[]40x x --=，find the value of 22212n x x x ++⋅⋅⋅+ C ）（6 points ）Find all ordered triples (,,)a b c of positive real that satisfy ：[]3a bc =，[]4a b c =，and []5ab c =上海中学自主招生试卷2018.031.因式分解：326114x x x -++=2.设0a b >>，224a b ab +=，则a b a b+=-3.若210x x +-=，则3223x x ++=4.已知21()()()4b c a b c a -=--，且0a ≠，则b c a +=5.一个袋子里装有两个红球和一个白球（仅颜色不同），第一次从中取出一个球，记下颜色后放回，摇匀，第二次从中取出一个球，则两次都是红球的概率是6.直线:l y =+x 、y 轴交于点A 、B ，AOB ∆关于直线AB 对称得到ACB ∆，则点C 的坐标是7.一张矩形纸片ABCD ，9AD =，12AB =，将纸片折叠，使A 、C 两点重合，折痕长是8.任给一个正整数n ，如果n 是偶数，就将它减半（即2n ），如果n 是奇数，则将它乘以3加1（即31n +），不断重复这样的运算，现在请你研究：如果对正整数n （首项）按照上述规则施行变换（注：1可以多次出现）后的第八项为1，则n 所有可能取值为9.正六边形ABCDEF 的面积是6平方厘米，联结AC 、CE 、EA 、BD 、DF 、FB ，求阴影部分小正六边形的面积为10.已知212(4)(4)y x m x m =+-+-与2y mx =在x 取任意实数时，至少有一个是正数，则m 的取值范围为11.已知a 、b 、c 是互不相等的实数，x 是任意实数，化简：222()()()()()()()()()x a x b x c a b a c c b a b c a c b ---++=------12.已知实数a 、b 满足221a ab b ++=，22t ab a b =--，则t 的取值范围是13.（1）求边长为1的正五边形对角线长；（2）求sin18︒.14.（1）32()f x x ax bx c =+++，0(1)(2)(3)3f f f <-=-=-≤，求c 的取值范围；（2）432()f x x ax bx cx d =++++，(1)10f =，(2)20f =，(3)30f =，求(10)(6)f f +-.15.我们学过直线与圆的位置关系，根据材料完成问题（1）（2）类似给出背景知识：平面:0Ax By Cz d α+++=；球：2222()()()x a y b z c R -+-+-=；点(,,)a b c 到平面:0Ax By Cz d α+++=的距离公式：d =；球心到平面的距离为d ，当d R <时，球与平面相交，当d R =时，球与平面相切，当d R >时，球与平面相离；问题（1）：若实数m 、n 、k 满足1m n k ++=，求222m n k ++的最小值；问题（21()2x y z +=++.参考答案1.(1)(34)(21)x x x --+2. 3.4 4.2 5.49 6.33(,227.4548.128、2、16、20、3、219.22cm 10.4m <11.112.133t -≤≤-13.（112+；（2）14-14.（1）69c <≤；（2）810415.（1）13；（2）123x y z =⎧⎪=⎨⎪=⎩上海中学自主招生试题1、因式分解：326114x x x -++= ．【答案】()()()13421x x x --+．【解析】容易发现1x =是方程3261140x x x -++=的解，因此原式可以提出因式(1)x -，得到2(1)(654)x x x ---，对2(654)x x --用十字相乘可以得到原式等于(1)(34)(21)x x x --+．2、设0a b >>，224a b ab +=，则a b a b +=- ．【解析】由条件可得2()6a b ab +=，2()2a b ab -=．因此22()63()2a b ab a b ab +==-．由于0a b +>，0a b ->，所以a b a b+=- 3、若210x x +-=，则3223x x ++=． 【答案】4．【解析】对多项式用带余除法可得32223(1)(1)4x x x x x ++=+-++，而由条件2(1)(1)0x x x +-+=，因此原式的值等于4．4、已知()()()24b c a b c a -=--，且0a ≠，则b c a+=_________． 【答案】2．【解析】令a b m -=，c a n -=，则c b m n -=+，代入()()()24b c a b c a -=--中得()24m n mn +=，()20m n ∴-=，m n ∴=， 即a b c a -=-，即2a b c =+，2b c a+∴=． 5、一个袋子里装有两个红球和一个白球（仅颜色不同），第一次从中取出一个球，记下颜色后放回，摇匀，第二次从中取出一个球，则两次都是红球的概率是． 【答案】49．【解析】第一次取出红球的概率为23，且无论第一次取出什么球，第二次取出红球的概率仍为23，因此两次都是红球的概率是224339⨯=． 6、直线:l y =与x 、y 轴交于点A 、B ，AOB ∆关于直线AB 对称得到ACB ∆，则点C 的坐标是 ．【答案】32⎛ ⎝⎭．【解析】根据函数解析式可以算出A 、B 的坐标分别为(1,0)A，B ．由于ACB 是AOB 关于直线AB 对称得到的，所以AC AO =，BC BO =．设(,)C m n，则可列方程组2222(1)1(3m n m n ⎧-+=⎪⎨+=⎪⎩，解得32m n ⎧=⎪⎪⎨⎪=⎪⎩O重合，舍去．因此3(2C ．7、一张矩形纸片ABCD ，9AD =，12AB =，将纸片折叠，使A 、C 两点重合，折痕长是． 【答案】454． 【解析】由题意知折痕是线段AC 的中垂线，设它与AB ,CD 分别交于,M N ．设MB x =，则由MC MA =可列方程2229(12)x x +=-，解得218x =．同理有218DN =．作ME CD ⊥，垂足为E ，则四边形MECB 是矩形，因此9ME BC ==，218CE BM ==．可知274NE CD DN CE =--=．而454MN ==．因此折痕长为454． 8、任给一个正整数n ，如果n 是偶数，就将它减半——得到2n ，如果n 是奇数，则将它乘以3加1——得到31n +，不断重复这样的运算，如果对正整数n （视为首项）按照上述规则实施变换后（有些书可能多次出现）的第8项为1，则n 的所有可能取值为________．【答案】128，21，20，3，16，2．【解析】设某一项为k ，则它的前一项应该为2k 或者13k -． 其中13k -必为奇数，即()4mod 6k ≡， 按照上述方法从1开始反向操作7次即可．9、正六边形ABCDED 的面积是6平方厘米，联结AC 、CE 、EA 、BD 、DF 、FB ，求阴影部分小正六边形的面积为． 【答案】22cm ．【解析】右图中，阴影部分是正六边形，且与正六边形 ABCDEF的相似比为1:3．因为 ABCDEF 的面积是26cm ，所以阴影部分的面积为2632()cm ÷=．10、已知()()21244y x m x m =+-+-与2y mx =在x 取任意实数时，1y ，2y 至少有一个是正数，m 的取值范围是________．【答案】4m <．【解析】取0x =，则14y m =-，20y =，40m ∴->，4m <，此时函数1y 的对称轴404m x -=-<， 则对任意0x ≥总有10y >，只需考虑0x <；若04m ≤<，此时20y ≤，则对任意0x <，有10y >，()()24840m m ∴∆=---<，解得04m ≤<； 若0m <，此时20y >对0x <恒成立；综上，4m <．11、已知a ，b ，c 是互不相等的实数，x 是任意实数，化简：()()()()()()()()()222x a x b x c a b a c c b a b c a c b ---++=------________． 【答案】1．【解析】令()()()()()()()()()()2222x a x b x c f x mx nx k a b a c c b a b c a c b ---=++=++------， ()()()1f a f b f c ∴===，即222111ma na k mb nb k mc nc k ⎧++=⎪++=⎨⎪++=⎩，01m n k ==⎧∴⎨=⎩ ，即()1f x ≡．12、已知实数a ，b 满足221a ab b ++=，22t ab a b =--，则t 的取值范围是________． 【答案】133t -≤≤-． 【解析】方法一：考虑基本不等式222a b ab +≥． 则2212a b ab ab +=-≥，则113ab -≤≤， 又2221t ab a b ab =--=-，133t ∴-≤≤-，其中1a =，1b =-时，3t =-成立；a b ==时，13t =-成立． 方法二：逆用韦达定理．12t ab +=，()2302t a b ++=≥，3t ∴≥-，a b +=，故a ,b 是方程2102t x ++=的两个根， 314022t t ++∴∆=-⨯≥，解得13t ≤-， 133t ∴-≤≤-．13、（1）求边长为1的正五边形对角线长；（2）求sin18︒．【答案】（1（2． 【解析】（1）设正五边形ABCDE ，联结,AC BE ，且设它们交于点M ．可以计算得到36ABM ABC ∠=∠=︒，因此ABM ACB ，可得2AB AM AC =⋅．同时，72BMC CBM ∠=∠=︒，所以BC MC =．若正五边形边长为1，则1AB BC CM ===，设AC x =，则由2AB AM AC =⋅可列方程21(1)x x =-，解得x去）． （2）根据诱导公式，sin18cos72︒=︒．在（1）的五边形中，BM AM AC CM ==-=．作CH BM ⊥，垂足为H ，则等腰三角形BMC 中12BH HM BM ===72CBM ∠=︒，所以sin18cos72BH BC ︒=︒==．14、（1）()32f x x ax bx c =+++，()()()01233f f f <-=-=-≤，求c 的取值范围；（2）()432f x x ax bx cx d =++++，()110f =，()220f =，()330f =，求()()106f f +-．【答案】（1）69c <≤ ；（2）8104．【解析】（1）()()()01233f f f <-=-=-≤， ()0f x k ∴-=有三个实根1,2,3x =---，()()()()123f x k x x x ∴-=+++，展开得6c k =+，69c ∴<≤；（2）方程()100f x x -=有三个实根1,2,3x =，记第4个根为x p =，则()()()()()10123f x x x p x x x -=----，()()()()()12310f x x p x x x x ∴=----+，()()()()()()()106109871006789608104f f p p ∴+-=-⨯⨯⨯++--⨯-⨯-⨯--=．15、我们学过直线与圆的位置关系，根据材料完成问题（1）（2）类似给出背景知识：平面:0Ax By Cz D α+++=；球：()()()2222x a y b z c R -+-+-=；点(),,a b c 到平面:0Ax By Cz D α+++=的距离公式：d =；球心到平面的距离为d ，当d R <时，球与平面相交，当d R =时，球与平面相切，当d R>时，球与平面相离；问题（1）：若实数m 、n 、k 满足1m n k ++=，求222m n k ++的最小值；问题（2）()12x y z =++． 【答案】（1）13；（2）123x y z =⎧⎪=⎨⎪=⎩． 【解析】（1）条件可转化为点(,,)m n k 在平面10x y z ++-=上，而222m n k ++的最小值即该点到原点距离平方的最小值．这个距离最小为原点到平面10x y z ++-=的距离，而原点到平面的距离可由材料公式计算得到：3d ==，因此222m n k ++的最小值为213d =，等号在13m n k ===时取到．（2）移项后配方可以得到2221111)1)1)0222-+-+=，因此必有101010-==-=，于是解得123xyz=⎧⎪=⎨⎪=⎩．上海中学自招试题1、因式分解：326114x x x -++=．2、设0a b >>，224a b ab +=，则a b a b +=- ．3、若210x x +-=，则3223x x ++=．4、已知()()()24b c a b c a -=--，且0a ≠，则b c a +=_________．5、一个袋子里装有两个红球和一个白球（仅颜色不同），第一次从中取出一个球，记下颜色后放回，摇匀，第二次从中取出一个球，则两次都是红球的概率是．6、直线:l y =+与x 、y 轴交于点A 、B ，AOB ∆关于直线AB 对称得到ACB ∆，则点C 的坐标是．7、一张矩形纸片ABCD ，9AD =，12AB =，将纸片折叠，使A 、C 两点重合，折痕长是．8、任给一个正整数n ，如果n 是偶数，就将它减半——得到2n ，如果n 是奇数，则将它乘以3加1——得到31n +，不断重复这样的运算，如果对正整数n （视为首项）按照上述规则实施变换后（有些书可能多次出现）的第8项为1，则n 的所有可能取值为________．9、正六边形ABCDED 的面积是6平方厘米，联结AC 、CE 、EA 、BD 、DF 、FB ，求阴影部分小正六边形的面积为．10、已知()()21244y x m x m =+-+-与2y mx =在x 1y ，2y 至少有一个是正数，m 的取值范围是________．11、已知a ，b ，c 是互不相等的实数，x 是任意实数，化简：()()()()()()()()()222x a x b x c a b a c c b a b c a c b ---++=------________．12、已知实数a ，b 满足221a ab b ++=，22t ab a b =--，则t 的取值范围是________．13、（1）求边长为1的正五边形对角线长；（2）求sin18︒．14、（1）()32f x x ax bx c =+++，()()()01233f f f <-=-=-≤，求c 的取值范围；（2）()432f x x ax bx cx d =++++，()110f =，()220f =，()330f =，求()()106f f +-．15、我们学过直线与圆的位置关系，根据材料完成问题（1）（2）类似给出背景知识：平面:0Ax By Cz D α+++=；球：()()()2222x a y b z c R -+-+-=；点(),,a b c 到平面:0Ax By Cz D α+++=的距离公式：d =；球心到平面的距离为d ，当d R <时，球与平面相交，当d R =时，球与平面相切，当d R>时，球与平面相离；问题（1）：若实数m 、n 、k 满足1m n k ++=，求222m n k ++的最小值；问题（2）()12x y z =++．2019年交大附中自招数学试卷一、填空题1、求值：cos30sin 45tan 60⋅⋅=.2、反比例函数1y x =与二次函数243y x x =-+-的图像的交点个数为.3、已知210x x --=，则3223x x -+=.4、设方程()()()()()()11111211210x x x x x x ++++++++=的两根为1x ，2x ，则()()1211x x ++=.5、直线y x k =+（0k <）上依次有,,,A B C D 四点，它们分别是直线与x 轴、双曲线k y x=、y 轴的交点，若AB BC CD ==，则k =.6、交大附中文化体行设施齐全，学生既能在教室专心学习，也能在操场开心运动，德智体美劳全面发展，某次体育课，英才班部分学生参加篮球小组、其余学生参加排球小组。

2017年上海市中学生业余数学学校预备年级招生考试试题（10月21日上午8:30~9:30）本卷满分100分（10’×10=100’）1.计算：（1）2017×20162016-2016×20172017=________.（2）1331215++++++=________.51326425865382.有一个四位正整数，在它的某位数字前加上一个小数点，再与这个四位数相加，得到数2037.17，则这个四位数是________.3.已知一列数：2017,2016,1,2015,20XX,1,20XX,20XX,1，…，3,2,1，则这一列数中，从左向右数，第2017个数是________.4.五年级某班有26名男生.在一次考试中，该班有30人得分超过85分，则这次考试中，该班女生中得分超过85分的人数比男生中得分没有超过85分的人数多________人.5.某人工作一月（按30天计算）的酬金是1800元加一台自动洗衣机.实际上，他做了12天，得到60元和一台自动洗衣机，则这台自动洗衣机的价值为________元.6.如图，在四边形ABCD中，已知AB=BC=a cm，AD=DC=b cm（a，b为整数），∠DAB=∠BCD=90°，且四边形ABCD的面积为385cm2，则四边形ABCD周长的最小值是________cm.7.有三堆棋子，每堆棋子一样多，且都由黑白两色棋子组成.已知第一堆的黑棋和第二堆的白棋数目相等，第三堆的黑.若把三堆棋占三堆全部黑棋的25棋子并成一堆，则在这一堆棋子中，白棋占全部棋子的________（填一个分数）.8.如图，由12条线段搭成一个空间框架.框架中两条没有公共端点的线段是不相交的，例如AC与BD是一对不相交的线段（这里AC，BD没有次序之分），则这个框架的12条线段中，不相交的线段有________对.9.在如图的10个小方格里分别填上1,2,3,4,5,11,12,13,14,15十个数，使三个2×2的正方形中的四个数的和都相等，则这个和的最大值是________. 10.有64个1×1×1的小正方体，其中34个是白色的，30个是黑色的.现将它们拼成一个4×4×4的大正方体，则大正方体表面黑色部分面积的最小是________.2017年上海市中学生业余数学学校高一年级招生考试试题（10月21日上午10:00~11:30）________区__________________学校，姓名___________准考证号________________得分评分 复核本卷满分100分（10’×10=100’） 1.如图，直线122y x =--与G 轴、y 轴分别交于 A 点、B 点，把△AOB （O 为坐标原点）沿直线AB翻折，点O 落在点C 处，则点C 的坐标是________.2.如图，直线AB 、AC 切圆O 于B 、C 两点，点P 在圆O 上，且到AB 、AC 的距离PM 、PN 分别为1、2，则点P 到直线BC 的距离PQ 的长为________.3.已知23()2|1|1,02f x x x x =---≤≤，则()f x 的值域是________. 4.已知a 、b 、G 、y 都是实数，且aG +by =4，aG 2+by 2=2，aG 3+by 3=1，则aG 4+by 4的值是________.5.如图，正方形DEFG 内接于△ABC ，正方形HIJ K内接于△AGF ，若BC=a ，KJ=m ，则正方形DEFG的面积为________.6.如图，在△ABC 中，∠ACB=90°，CA=CB=2，O 为AC 的中点，以AC 为直径作⊙O ，OB 交⊙O 于点D ，AD 的延长线交CB 于点E ，则CE 的长为________.7.一个五位数乘以某一整数k （28k ≤≤），得到该五位数的反序数（把一个n 位正整数的各位数码顺序颠倒过来得到的新的n 位整数称为原数的反序数. 例如12345的反序数为54321），则原来的五位数是________________.8.已知a 、b 为实数，且224a ab b ++=，则22a ab b -+的取值范围为 ________________.9.从集合{|,11000}x x N x ∈≤≤中取出k 个数，使得取出的k 个数中，任意三 个数之和总能被18整除，则k 的最大值为________.10.已知凸五边形ABCDE 的面积为1，且△ABC,△BCD,△CDE,△DEA,△EAB 的 面积都相等，则△ABC 的面积为________.2017年上海市中学生业余数学学校招生试题答案预备年级1.（1）0;（2）242.20173.6734.45.11006.927.948.36 9.3310.22高一年级 1.)516,58(-- 2.2 3.[-2,1]4.21 5.am6.15- 7.219788.[34,12] 9.5610.1055-。

2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题（54分）1、不等式1>x 的解集为______________；2、计算：_________213lim=+-∞→n n n ；3、设集合{}20<<=x x A ，{}11<<-=x x B ，则________=B A ；4、若复数i z +=1（是虚数单位），则______2=+zz ； 5、已知{}n a 是等差数列，若1082=+a a ，则______753=++a a a ;6、已知平面上动点到两个定点()0,1和()0,1-的距离之和等于4，则动点的轨迹方程为_________;7、如图，在长方体1111D C B A ABCD -中，3=AB ，4=BC ，51=AA ，是11C A 的中点,则三棱锥11OB A A -的体积为_________；第7题图 第12题图8、某校组队参加辩论赛，从6名学生中选出4人分别担任一、二、三、四辩，若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________（结果用数值表示)。

9、设R a ∈，若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等，则_______=a ；10、设R m ∈，若是关于的方程0122=-++m mx x 的一个虚根，则-z 的取值范围是________;11、设0>a ，函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点，则的取值范围是__________；12、如图,在正方形ABCD 的边长为米，圆的半径为1米,圆心是正方形的中心,点、分别在线段AD 、上,若线段PQ 与圆有公共点，则称点在点的“盲区”中，已知点以1。

5米/秒的速度从出发向移动,同时，点以1米/秒的速度从出发向移动，则在点从移动到的过程中,点在点的盲区中的时长均为_____秒(精确到0。

2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题（54分）1、不等式1>x 的解集为______________；2、计算:_________213lim=+-∞→n n n ；3、设集合{}20<<=x x A ，{}11<<-=x x B ,则________=B A ；4、若复数i z +=1（i 是虚数单位),则______2=+zz ； 5、已知{}n a 是等差数列，若1082=+a a ，则______753=++a a a ；6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4，则动点P 的轨迹方程为_________；7、如图,在长方体1111D C B A ABCD -中，3=AB ，4=BC ，51=AA ，O 是11C A 的中点，则三棱锥11OB A A -的体积为_________；第7题图 第12题图8、某校组队参加辩论赛，从6名学生中选出4人分别担任一、二、三、四辩，若其中学生甲必须参赛且不担任四辩，则不同的安排方法种数为_____________（结果用数值表示）。

9、设R a ∈，若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等，则_______=a ;10、设R m ∈，若z 是关于x 的方程0122=-++m mx x 的一个虚根，则-z 的取值范围是________；11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则a 的取值范围是__________；12、如图，在正方形ABCD 的边长为20米，圆O 的半径为1米，圆心是正方形的中心，点P 、Q 分别在线段AD 、CB 上，若线段PQ 与圆O 有公共点，则称点Q 在点P 的“盲区”中，已知点P 以1.5米/秒的速度从A 出发向D 移动，同时，点Q 以1米/秒的速度从C 出发向B 移动，则在点P 从A 移动到D 的过程中，点Q 在点P 的盲区中的时长均为_____秒（精确到0.1）. 二．选择题（20分）13. 下列函数中，为偶函数的是（ ）A 2-=x y B 31x y = C 21-=xy D 3x y =14. 如图，在直三棱柱111C B A ABC -的棱所在的直线中,与直线1BC 异面的直线的条数为( ） A 1 B 2 C 3 D 415. 若数列}{n a 的前n 项和，“}{n a 是递增数列”是“}{n S 是递增数列”的（ ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 即不充分也不必要条件16、已知A 、B 是平面内两个定点，且2=→AB ，该平面上的动线段PQ 的两个端点P 、Q 满足：5≤→AP ，6=⋅→→AB AP ，→→-=AP AQ 2,则动线段PQ 所围成的面积为( ）A 、50B 、60C 、72D 、108三、解答题(14+14+14+16+18=76分） 17、已知x x f cos )(=（1）.若31)(=αf ，且],0[πα∈，求)3(πα-f 的值； （2）。

2004年上海市中学生业余数学学校高一年级招生试题（考试时间：2014年10月12日）1、如图，在直角坐标平面中，30AOX ∠=︒，AB AO ⊥，2AO =，BO =，则点B 的坐标为 ▲ ． 2、记N i k *∈，且12n k k k >>>L ，若122014222n k k k =+++L ，试求12n k k k +++L 的值为 ▲ ． 3、如图，在矩形ABCD 中，5AB =，12BC =，将矩形沿对角线AC 翻折，记D 的对应点为点E ，联结AE 交BC 于点F ，则△ECF 的面积为 ▲ ．4、若方程220x ax ++=，20x ax a +-=，2(1)0x a x a +--=中至少有一个方程有实数根，则a 的取值范围是 ▲ ．5、若111111(20)a b c d e a b c d e =++++<<<<<，满足 ,,,,N a b c d e *∈，试写出满足条件的其中一个算式 ▲ ．6、如图，四边形ABCD 是正方形，E 是边BC 上的一点，且40DME S =△，20AB =，则BE 的长为 ▲ ．7、若方程20x mx n --=的正根小于5，且,N m n *∈，则满足条件的方程共有 ▲ 个8、令函数110()10100x f x x +=-，记()()((()))n n ff x f f f f x =L 14243个，则 (2)(3)(1000)11112222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L 的值为 ▲ ． 9、若正整数n 满足如下条件：①不等式220130x x n -+>对于N x *∈恒成立；②存在N x *∈，使得220140x x n -+≤成立。

则满足条件的n 的个数是 ▲ ．10、已知x 是无理数，且满足2x x +、322x x +都是整数，则x 的值为 ▲ ．AB CD E F A B CDE M。