第十四章 轴向压杆的稳定计算
- 格式:doc
- 大小:96.50 KB
- 文档页数:7




压杆稳定性计算公式例题在工程结构设计中,压杆是一种常见的结构元素,用于承受压力和稳定结构。
在设计过程中,需要对压杆的稳定性进行计算,以确保结构的安全性和稳定性。
本文将介绍压杆稳定性计算的基本原理和公式,并通过一个例题进行详细说明。
压杆稳定性计算的基本原理。
压杆稳定性是指压杆在受压力作用下不会发生侧向屈曲或失稳的能力。
在进行压杆稳定性计算时,需要考虑压杆的材料、截面形状、长度、支座条件等因素,以确定其稳定性。
一般来说,压杆的稳定性可以通过欧拉公式或约束条件来计算。
欧拉公式是描述压杆稳定性的经典公式,其表达式为:Pcr = (π^2 E I) / (K L)^2。
其中,Pcr表示压杆的临界压力,E表示弹性模量,I表示截面惯性矩,K表示约束系数,L表示压杆的有效长度。
这个公式是基于理想的弹性理论,适用于较长的细杆,但在实际工程中,压杆的稳定性计算可能还需要考虑其他因素。
除了欧拉公式外,压杆稳定性计算还需要考虑约束条件。
约束条件是指压杆在受力时的支座和边界条件,对压杆的稳定性有重要影响。
在实际工程中,约束条件可以通过有限元分析等方法来确定,以获得更精确的稳定性计算结果。
压杆稳定性计算的例题分析。
下面我们通过一个例题来说明压杆稳定性计算的具体步骤和方法。
假设有一根长度为2m的钢质压杆,截面形状为矩形,截面尺寸为100mm ×50mm,弹性模量为2.1 × 10^5 N/mm^2。
现在需要计算在这根压杆上施加的最大压力,使得其不会发生侧向屈曲或失稳。
首先,我们需要计算压杆的有效长度。
对于简支压杆,其有效长度可以通过以下公式计算:Le = K L。
其中,K为约束系数,对于简支压杆,K取1。
所以,这根压杆的有效长度为2m。
接下来,我们可以使用欧拉公式来计算压杆的临界压力。
根据欧拉公式,可以得到:Pcr = (π^2 E I) / L^2。
其中,E为弹性模量,I为截面惯性矩。
根据矩形截面的惯性矩公式,可以计算得到I = (1/12) b h^3 = (1/12) 100mm (50mm)^3 = 5208333.33mm^4。






第十四章轴向压杆的稳定计算【教学要求】了解压杆稳定与失稳的概念;理解压杆的临界力和临界应力的概念;能采用合适的公式计算各类压杆的临界力和临界应力;熟悉压杆的稳定条件及其应用;了解提高压杆稳定性的措施。
【重点】1、计算临界力。
2、掌握折减系数法对压杆进行稳定设计与计算的基本方法【难点】折减系数法对压杆进行稳定设计与计算的基本方法。
【授课方式】课堂讲解【教学时数】共计4学时【教学过程】•14.1 压杆稳定的基本概念0.5学时•14.2 压杆的临界力和临界应力 1.5学时★14.3 压杆的稳定条件及其应用 1.5学时•14.4 提高压杆稳定性的措施0.5学时【小结】【课后作业】•14.1 压杆稳定的基本概念•• 有实例提出问题,总结引申新的课题。
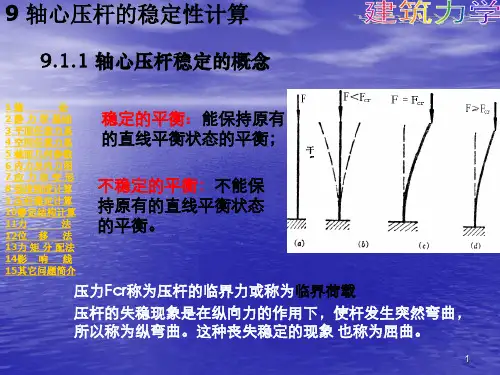
1、概念压杆稳定性:压杆保持其原来直线平衡状态的能力。
压杆不能保持其原来直线平衡状态而突然变弯的现象,称为压杆的直线平衡状态丧失了稳定,简称为压杆失稳。
研究压杆稳定性的意义:压杆因强度或刚度不足而造成破坏之前一般都有先兆;压杆由于失稳而造成破坏之前没有任何先兆,当压力达到某个临界数值时就会突然破坏,因此这种破坏形式在工程上具有很大的破坏性。
在建筑工程中的受压上弦杆、厂房的柱子等设计中都必须考虑其稳定性要求。
2、平衡状态的稳定性当P <cr P ,时,是稳定平衡状态当P =cr P 时,是随遇平衡状态,这种状态称为临界平衡状态 当P >cr P 时,是不稳定平衡状态当P =cr P 时,压杆的平衡状态是介于稳定和不稳定之间的临界平衡状态,因此定值cr P 。
3、压杆临界力F cr14.2 压杆的临界力和临界应力 临界力的影响因素临界力F cr 的大小反映了压杆失稳的难易,而压杆失稳就是直杆变弯,发生弯曲变形,因此临界力的大小与影响直杆弯曲变形的因素有关: 杆的长度l 、抗弯刚度EI 、杆端支承。
14.2.1临界力的欧拉公式22()cr EIP l πμ=适用条件:弹性范围内。
式中,EI 称为压杆的抗弯刚度, I 是截面对形心轴最小的惯性矩。
lμ称为压杆的计算长度, μ称为长度系数,是与杆端支承情况有关的量例14.1 一根两端铰支的№20a工字钢细长压杆,长l=3m,钢的弹性模量E=200GPa,试计算其临界力。
解查型钢表得Iz=2370cm4,Iy=158cm4由此可知,若轴向压力达到346kN时,此杆会失稳。
例14.2 一矩形截面的中心受压的细长木柱,长l=8m,柱的支承情况,在最大刚度平面内弯曲时为两端铰支(图a);在最小刚度平面内弯曲时为两端固定(图b)。
木材的弹性模量E=10GPa,试求木柱的临界力。
解由于最大刚度平面与最小刚度(1)计算最大刚度平面内的临界力截面的惯性矩为两端铰支,长度系数μ=1(2)计算最小刚度平面内的临界力。
两端固定,长度系数μ=0.5比较计算结果可知,第一种情况的临界力小,所以压杆失稳时将在最大刚度平面内产生弯曲。
此例说明,当在最小刚度平面与最大刚度平面内支承情况不kN346N10346N310158102003289222=⨯=⨯⨯⨯⨯==-ππlEIFcr454743m108mm108mm12200120-⨯=⨯=⨯=yIkN123N10123N)81(108101014.3)(3259222=⨯=⨯⨯⨯⨯⨯==-lEIF ycrμπ454743m1088.2mm1088.2mm12120200-⨯=⨯=⨯=ZIkN177N10177N)85.0(1088.2101014.3)(3259222=⨯=⨯⨯⨯⨯⨯==-lEIF Zcrμπ同时,压杆不一定在最小刚度平面内失稳,必须经过具体计算后才能确定。
14.2.2 临界应力A l EI A P Cr cr22)(μπσ==引入截面的惯性半径iA I i =于是临界应力可写为2222)()(il E Al EI crμπμπσ==令i lμλ=则有22λπσE cr =上式为计算细长压杆临界应力的欧拉公式,式中A 称为压杆的柔度(又称为长细比)。
柔度是量纲为1的量,它综合反映了压杆的支承情况、杆长及横截面的形状和尺寸等因素对临界应力的影响。
由式可知,压杆的柔度越大,其临界应力越小.压杆越容易失稳。
所以,柔度是衡量压杆稳定性的一个重要参数。
14.2.3 欧拉公式的适用范围即:——对应于材料比例极限时的柔度,只与材料的性质有关,与压杆的截面形状和尺寸无关。
14.2.4 超出比例极限时压杆的临界应力、临界应力总图压杆的应力超出比例极限时(λ<λp ),这类杆件工程上称为中柔度杆,此类压杆的稳定称弹塑性稳定。
抛物线公式(经验公式)σcr = a - b λ2【小 结】p cr Eσλπσ≤=22pp σπλλE=≥pλ1、细长压杆的临界力(临界应力)用欧拉公式计算。
欧拉公式是材料服从胡克定律的条件下导出的,所以,只有当P P cr λλσσ≥即, 时,欧拉公式才能适用。
22()cr EI P l πμ=,22λπσE cr =2、柔度是压杆稳定计算中的重要参数。
它综合反映了压杆的长度、支承情况、截面形状及尺寸对压杆稳定性的影响。
li μλ=,A I i =【课后作业】教材:P32,习题1.★14.3 压杆的稳定条件及其应用14.3.1 压杆稳定条件[]PA σϕσ=≤ϕ-----材料的折减系数。
当材料一定时,折减因数ϕ的值取决于柔度λ,λ值越大ϕ值越小,且ϕ值在0-1之间变化。
14.3.2 压杆稳定条件的应用 1、稳定校核。
2.设计截面。
3.确定稳定许用荷载。
例 14-3 一圆形木柱高6m ,直径d=20cm,两端铰支,承受轴向压力P=50kN,木材的许可应力[σ]=10Mpa.校核该柱的稳定性。
解 (1)计算截面的惯性半径54d i cm ====(2)计算柔度λ。
因两端铰支,1μ=,所以16001205liμλ⨯===(3)查折减系数ϕ。
从表11-2中查得ϕ=0.209。
(4)稳定校核3225010 1.59 1.592004[]0.20910 2.09P N MPa mm A MPa σπϕσ⨯====⨯=⨯=因此,[]σϕσ ,木柱满足稳定条件。
14.4 提高压杆稳定性的措施1、减小压杆的支承长度2、改善支承情况 ,减小长度系数μ3、选择合理的截面形状当截面面积相同的情况下,增大惯性矩I ,从而达到增大惯性半径i ,减小柔度λ,提高压杆的临界应力。
当压杆在各个弯曲平面内的支承条件相同时,压杆的稳定性是由I min 方向的临界应力控制。
因此,应尽量使截面对任一形心主轴的惯性矩相同,这样可使压杆在各个弯曲平面内具有相同的稳定性。
4、合理选择材料对于大柔度杆,临界应力与材料的弹性模量E 有关,由于各种钢材的弹性模量E 值相差不大。
所以,对大柔度杆来说,选用优质钢材对提高临界应力意义不大。
对于中柔度杆,其临界应力与材料强度有关,强度越高的材料,临界应力越高。
所以,对中柔度杆而言,选择优质钢材将有助于提高压杆的稳定性。
【小 结】1、压杆稳定计算。
工程中常采用折减系数法进行计算。
压杆的稳定条件是[]PA σϕσ=≤折减系数ϕ因材料而不同,随柔度而变化。
2、提高压杆的稳定性可采用以下措施:1、选择合理的截面形状;2、减小压杆长度;3、改善支承情况;4、选择适当的材料。
【课后作业】教材:P32,习题8.。