压杆稳定性计算

压杆稳定性验算公式压杆稳定性是工程结构设计中需要考虑的一个重要问题。

在许多工程应用中，压杆一般用于承受压力作用的结构元素，如柱子、桁架等。

压杆的稳定性验算是为了判断压杆在承受压力时是否会发生屈曲或失稳的现象，需要通过计算并比较压力作用下的抗弯稳定能力和压杆的承载能力。

压杆在弯曲中的稳定性主要受压杆的几何形状、材料特性、边界条件以及压力作用方向等因素的影响。

一般来说，压杆的稳定性验算可以采用欧拉公式、约束系数法和有限元法等方法进行。

欧拉公式是一种经典的压杆稳定性验算方法，其基本原理是根据压杆的截面形状和尺寸来计算压杆的临界压力，然后和实际压力进行比较，从而评估压杆的稳定性。

欧拉公式的基本形式如下：Pcr = (π^2EI)/(kl)^2其中Pcr为压杆的临界压力（也称为临界载荷）E为材料的弹性模量I为压杆的截面惯性矩k为约束系数（取决于边界条件，一般为纵横比的函数）l为压杆的有效长度。

欧拉公式适用于压杆为理想长细杆的情况，即压杆的长度远大于其截面的最小尺寸，并且边界条件是固定或铰支的。

对于实际情况下的压杆验算，可以根据具体条件和要求进行修正或改进。

约束系数法是一种更为精确的压杆稳定性验算方法，它考虑了压杆的几何形状、材料特性以及边界条件等因素的影响。

其基本原理是根据压杆的几何形状以及约束条件，在一系列已知的稳定压力下进行试算，从而得到压力-破坏应力的关系曲线。

然后根据工程要求，找到落在这条曲线上的设计压力，从而评估压杆的稳定性。

约束系数法的计算过程较为复杂，需要进行较多的计算和试算，但可以得到更为准确的结果。

在实际工程中，一般可以借助计算机辅助设计软件进行约束系数法的计算。

有限元法是一种现代化的验算方法，通过将大型结构划分为小型有限元，然后进行数值计算，得到压杆的应力和变形情况，从而评估压杆的稳定性。

有限元法充分考虑了压杆的复杂几何形状、材料非线性以及边界条件的影响，具有较高的精度和适用性。

以上介绍的是压杆稳定性验算的一些基本方法和原理。

压杆稳定计算公式一般而言，压杆的稳定性计算可以分为以下几个步骤：1.确定杆件几何形状：包括杆件的长度、截面形状和尺寸等参数。

这些参数对杆件的承载能力和稳定性有很大影响。

2.确定杆件材料的特性：主要包括弹性模量、截面惯性矩和截面面积等。

这些参数主要用于计算杆件的刚度和强度。

3.确定受力条件：包括受力的方向、大小和位置等参数。

这些参数是计算杆件临界载荷的基础。

4.计算临界载荷：可以使用公式或者数值方法计算出杆件的临界载荷。

压杆的临界载荷一般通过欧拉公式计算得到。

当临界载荷小于或等于实际受力时，杆件保持稳定；当临界载荷大于实际受力时，杆件可能发生屈曲。

欧拉公式是压杆稳定计算中最常用的公式之一，其基本形式为：Pcr = (π²EI) / (KL)²其中，Pcr为杆件的临界载荷，E为材料的弹性模量，I为杆件的截面惯性矩，K为端部条件系数，L为杆件的长度。

端部条件系数K取决于杆件的端部支承情况，常见的取值有：-简支-简支（K=1.0）-固支-固支（K=0.5）-简支-固支（K=0.699）-无端支承（K=π/2）实际工程设计中，常通过杆件的截面形状和尺寸、受力条件等参数来选择合适的端部条件系数。

需要注意的是，以上公式和计算方法适用于理想化的压杆情况，不考虑非理想因素和杆件的浮动性。

在实际工程中，还需要结合具体情况进行综合分析和计算。

总之，压杆稳定计算是工程设计中非常重要的一环，可以通过计算杆件的临界载荷来判断杆件在受压状态下是否能够保持稳定。

通过合理选择杆件的截面形状和尺寸、材料的特性以及受力条件等参数，并结合压杆的端部支承情况，可以进行准确的压杆稳定计算。

压杆稳定性计算公式例题在工程结构设计中，压杆是一种常见的结构元素，用于承受压力和稳定结构。

在设计过程中，需要对压杆的稳定性进行计算，以确保结构的安全性和稳定性。

本文将介绍压杆稳定性计算的基本原理和公式，并通过一个例题进行详细说明。

压杆稳定性计算的基本原理。

压杆稳定性是指压杆在受压力作用下不会发生侧向屈曲或失稳的能力。

在进行压杆稳定性计算时，需要考虑压杆的材料、截面形状、长度、支座条件等因素，以确定其稳定性。

一般来说，压杆的稳定性可以通过欧拉公式或约束条件来计算。

欧拉公式是描述压杆稳定性的经典公式，其表达式为：Pcr = (π^2 E I) / (K L)^2。

其中，Pcr表示压杆的临界压力，E表示弹性模量，I表示截面惯性矩，K表示约束系数，L表示压杆的有效长度。

这个公式是基于理想的弹性理论，适用于较长的细杆，但在实际工程中，压杆的稳定性计算可能还需要考虑其他因素。

除了欧拉公式外，压杆稳定性计算还需要考虑约束条件。

约束条件是指压杆在受力时的支座和边界条件，对压杆的稳定性有重要影响。

在实际工程中，约束条件可以通过有限元分析等方法来确定，以获得更精确的稳定性计算结果。

压杆稳定性计算的例题分析。

下面我们通过一个例题来说明压杆稳定性计算的具体步骤和方法。

假设有一根长度为2m的钢质压杆，截面形状为矩形，截面尺寸为100mm ×50mm，弹性模量为2.1 × 10^5 N/mm^2。

现在需要计算在这根压杆上施加的最大压力，使得其不会发生侧向屈曲或失稳。

首先，我们需要计算压杆的有效长度。

对于简支压杆，其有效长度可以通过以下公式计算：Le = K L。

其中，K为约束系数，对于简支压杆，K取1。

所以，这根压杆的有效长度为2m。

接下来，我们可以使用欧拉公式来计算压杆的临界压力。

根据欧拉公式，可以得到：Pcr = (π^2 E I) / L^2。

其中，E为弹性模量，I为截面惯性矩。

根据矩形截面的惯性矩公式，可以计算得到I = (1/12) b h^3 = (1/12) 100mm (50mm)^3 = 5208333.33mm^4。

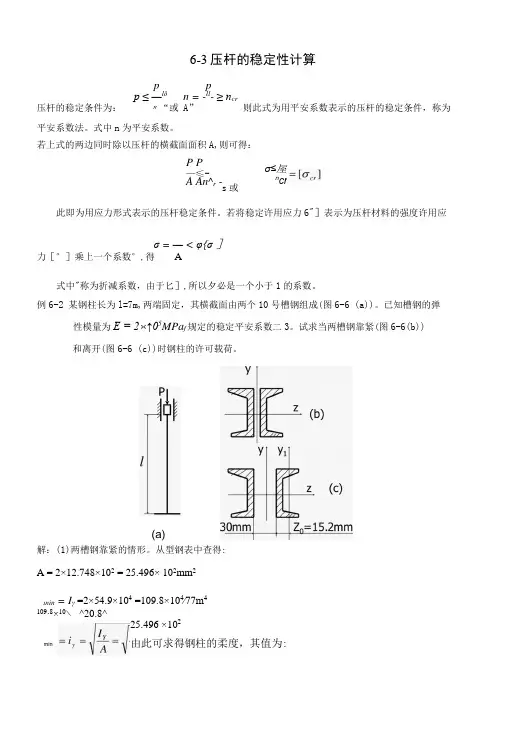
6-3压杆的稳定性计算p p p ≤ —lδn = -ll - ≥ n cr压杆的稳定条件为： 〃“或 A”则此式为用平安系数表示的压杆的稳定条件，称为 平安系数法。

式中n 为平安系数。

若上式的两边同时除以压杆的横截面面积A,则可得：P P—≤- A An^r - s 或 此即为用应力形式表示的压杆稳定条件。

若将稳定许用应力6"］表示为压杆材料的强度许用应σ = — < φ{σ ］力［°］乘上一个系数°,得 A式中"称为折减系数，由于匕］,所以夕必是一个小于1的系数。

例6-2 某钢柱长为l=7m,两端固定，其横截面由两个10号槽钢组成(图6-6 (a))。

已知槽钢的弹性模量为E = 2×↑05MPa f 规定的稳定平安系数二3。

试求当两槽钢靠紧(图6-6(b))和离开(图6-6 (c))时钢柱的许可载荷。

解：(1)两槽钢靠紧的情形。

从型钢表中查得:A = 2×12.748×102 = 25.496× 102mm 2ιnin = I γ =2×54.9×104 =109.8×104∕77m 4 109∙8×10∖ ^20.8^25.496 ×102由此可求得钢柱的柔度，其值为:σ≤屋 n cr (a)min故该钢柱为大柔度杆，可用欧拉公式（6-2）计算临界力。

P 176 9P } ≤H = -^ = 58.97ZN由公式（6-8）计算钢柱的许可载荷P,即： 3（2）两槽钢离开情形。

从型钢表中可查得：L =2×198×104 =396×104m∕∕744∕v =2 J. + —+ z 0 ×12.748×102，51I 2 0J _B =2[25.6×104+(15 + l5.2)2 × 12.748× 102=283.7 ×104mm 4283.7 ×104 ” zi=33Amm A 25.496 ×102比较以上数值可知，应取min】μl 0.5 × 7000 /。

压杆稳定性计算范文
首先，我们需要确定压杆的受力情况。

根据受力情况的不同，压杆可
以分为受弯杆、压弯杆和压缩杆。

其中，受弯杆在一端受到的是单向弯矩，压弯杆在两端受到相等大小的对称弯矩，压缩杆在两端受到相等大小的压力。

受弯杆的稳定性计算可以根据欧拉公式进行，即：
Pcr = (π^2 * E * I) / L^2
其中，Pcr为压弯杆的临界载荷，E为材料的弹性模量，I为截面的
惯性矩，L为杆的长度。

压弯杆的稳定性要求：
P < Pcr
其中，P为实际作用在杆上的载荷。

压缩杆的稳定性计算可以使用欧拉公式或安全系数法进行。

欧拉公式
可以描述为：
Pcr = (π^2 * E * A) / (K * L)^2
其中，Pcr为压缩杆的临界载荷，E为材料的弹性模量，A为截面的
面积，K为杆的有效长度系数，L为杆的长度。

压缩杆的稳定性要求：
P < Pcr
P < Pallow = Pcr / S
其中，P为实际作用在杆上的载荷，Pallow为允许的压缩载荷，S为
材料的安全系数。

此外，压杆的相对稳定性也需要考虑。

相对稳定性是指杆的截面形状
与载荷作用方向之间的关系。

如果载荷作用方向与截面形状的对称轴垂直，压杆将具有较大的稳定性；如果载荷作用方向与截面形状的对称轴平行或
接近平行，压杆将具有较小的稳定性。

总之，压杆稳定性计算是确保结构安全性的重要环节。

通过合理选择
杆材、计算受力状况和结构参数，可以预测并满足压杆的稳定性要求，从
而保证结构的工作正常和安全。

压杆稳定系数
压杆稳定系数是指在压杆受力时，其稳定性的能力。

在机械设计中，压杆通常用于承受压缩力，如桥梁、大型机器等结构中。

由于受到外界因素的影响，如温度变化、弯曲、振动等，会导致压杆发生变形或失稳。

因此，为了确保结构的安全性和稳定性，在设计中需要考虑到压杆的稳定系数。

一般来说，压杆稳定系数可以通过计算得出。

其计算公式为：
K = (π^2 × E × I) / (l / r)^2
其中，K表示压杆的稳定系数；E表示弹性模量；I表示截面惯性矩；l 表示压杆长度；r表示截面半径。

从公式中可以看出，当弹性模量或截面惯性矩增大时，稳定系数也会随之增大。

而当长度或截面半径减小时，稳定系数也会随之减小。

除了计算方法外，在实际应用中还需要注意以下几点：
1. 压杆截面形状应尽可能地规则和对称，并且要尽可能地保持圆形或矩形。

这样可以减小压杆的失稳风险。

2. 压杆的长度应尽可能地短，避免过长的压杆容易发生弯曲或振动，从而导致失稳。

3. 在设计中要考虑到压杆所受到的外力和载荷，并根据实际情况进行合理的选择和计算。

4. 在制造和安装过程中要保证压杆的质量和精度，避免因为制造误差或安装不当导致失稳风险增加。

总之，压杆稳定系数是机械设计中非常重要的一个指标。

通过合理地选择和计算，可以确保结构的安全性和稳定性，从而达到更好的使用效果。