压杆稳定性计算汇总精编版

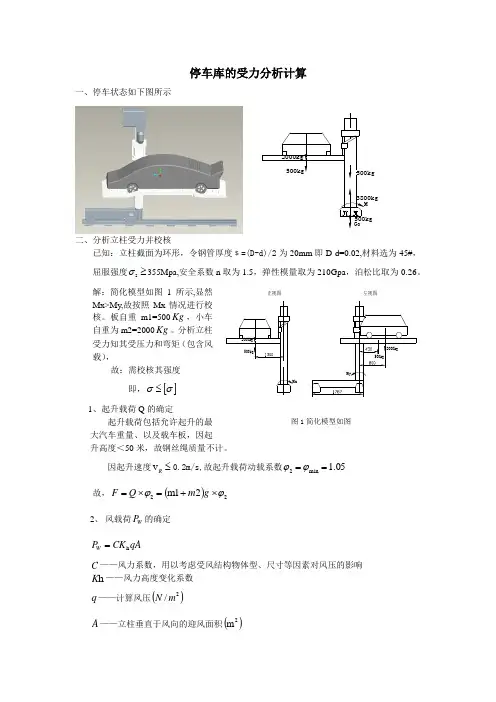
2000kg 500kg500kg3800kg G 3500kg M 停车库的受力分析计算一、停车状态如下图所示二、分析立柱受力并校核已知：立柱截面为环形，令钢管厚度﹩=(D-d)/2为20mm 即D-d=0.02,材料选为45#，屈服强度s σ≥355Mpa,安全系数n 取为1.5，弹性模量取为210Gpa ，泊松比取为0.26。

解：简化模型如图1所示,显然Mx>My,故按照Mx 情况进行校核。

板自重m1=500Kg ，小车自重为m2=2000Kg 。

分析立柱受力知其受压力和弯矩（包含风载），故：需校核其强度即，[]σσ≤1、起升载荷Q 的确定起升载荷包括允许起升的最大汽车重量、以及载车板，因起升高度＜50米，故钢丝绳质量不计。

因起升速度≤R v 0.2m/s,故起升载荷动载系数2ϕ05.1min ==ϕ故，()2221m ϕϕ⨯+=⨯=g m Q F2、 风载荷W P 的确定qA CK P W h =C ——风力系数，用以考虑受风结构物体型、尺寸等因素对风压的影响 h K ——风力高度变化系数q ——计算风压()2/m NA ——立柱垂直于风向的迎风面积()2m2000kg2000kg 500kg正视图左视图Mx500kgMy图1简化模型如图1） 计算风压q风压计算公式为 2613.0q v =风压按照沿海地区工作状态风压计算v=20m/s,故q=245.22m /N风压按照工作状态下的最大计算风压计算，此时q 取2502m /N ，故最终q 取2502m /N 。

2） 风力系数C因为离地面高度≤10m,按照海上及海岛2.010⎪⎭⎫⎝⎛h ，风压高度变化系数h K 取1.00因为是圆管结构且10q 2≈d （q 为计算风压，d 为圆管直径），故C 取0.9 3） 迎风面积At A A ψ=ψ——结构的充实率，tA A=ψ，钢管桁架结构ψ值取0.2-0.4，故0.3 t A ——结构或物品外形轮廓面积在垂直于风向平面上的投影()2m h D A t =()2m D ——立柱外径；h ——立柱高度 D D qA CK P W 675325000.19.0h =⨯⨯⨯⨯==3、 强度校核1[]nsσσσ=≤即[]σσ≤+=W M A F maxcmax令WM A F +=σ 2ϕ⨯=Q F ;()g m m Q 21+=()224d D A -=π21M M M += M1——由重力引起的弯矩；M2——由风载引起的弯矩()3.121m 1⨯+=g m M ;h P M W *=212⎪⎪⎭⎫ ⎝⎛-=443d 132D D W π ()()⎪⎪⎭⎫⎝⎛-*+⨯++-=+=443222d 132213.121m 4D D hP g m d D Q W M A F W ππϕσ=()()[]()()⎪⎪⎭⎫ ⎝⎛--*⨯+⨯++--*+D D D hD g m D D g m 4322204.032675213.121m 04.0421m ππϕ将m1=500kg, m2=2000kg, g=9.8N/kg, h=3m,2ϕ=0.5 代入上式， 令[]nsσσσ=≤得m 1202.0≥D4、 强度校核2[]nsσσσ=≤即[]σσ≤+=WM A F maxcmax 令WM A F +=σ 2ϕ⨯=Q F ;()g m m Q 21+=()224d D A -=π2221M M M += M1——由重力引起的弯矩；M2——由风载引起的弯矩()3.121m 1⨯+=g m M ;h P M W *=212 ⎪⎪⎭⎫ ⎝⎛-=443d 132D D W π ()()[]⎪⎪⎭⎫ ⎝⎛-⎥⎦⎤⎢⎣⎡*+⨯++-=+=44322222d 132213.121m 4D D h P g m d D Q W M A F W ππϕσ=()()[]()[]()⎪⎪⎭⎫ ⎝⎛--⎥⎦⎤⎢⎣⎡*⨯+⨯++--*+D D D h D g m D D g m 432222204.032675213.121m 04.0421m ππϕ 将m1=500kg, m2=2000kg, g=9.8N/kg, h=3m,2ϕ=0.5 代入上式， 令[]nsσσσ=≤得m 1200.0≥D5、压杆稳定性校核：将立柱简化为一端固定，另一端自由的杆件，故压杆的长度因素μ取2.临界压力与工作压力之比即为压杆的工作安全系数，他应大于规定的稳定安全系数st n ，故有crst F n n F=≥，这里取st n =4.立柱承受的轴向压力为()212*(5002000)*9.8*1.0525725F m m g N ϕ=+=+=若在稳定条件中取等号，则立柱的临界压力应该是cr 4*25725102900st F n F N === ①由欧拉公式求得临界压力为()()()29442cr 22210106423D d EIF l πππμ⨯⨯⨯-==⨯ （D=d+0.04 m ）②由①、②两式解0.07887D m = 取0.08D m =用所确定的D 计算立柱的柔度 liμλ=因为0.0116i ===== 故23517.240.0116liμλ⨯===对于材料45#钢来说，由公式求得176.41λ=== 由于1λλ>，所以前面用欧拉公式进行计算是正确的。

后支撑压杆稳定性计算:1.后支撑的截面系数：2.后支撑的长度：假设后支撑的长度L=1325mm3.后支撑所受的压力：假设后支撑所受的压力F1：F1= 3702 N后支撑主要受压力的作用，需校验其抗压性，即压杆稳定。

4.压杆的3种类型：a.大柔度杆b.中柔度杆c.小柔度杆5.压杆的柔度由下式算出：λ：柔度μ：压杆的长度因素l: 压杆的长度i ： 压杆的惯性半径6.压杆类型的判定：a.λ≥λ1，判定为大柔度杆b.λ 2 <λ<λ1，判定为中柔度杆c. λ≤λ2，判定为小柔度杆(说明：λ1、λ2与材料的性质有关，不同的材料有不同的取值。

i l μλ=材质Q235B: λ1=100; λ2=62材质硬铝：λ1=55；λ2=0)7.压杆临界力计算：a. 大柔度杆 : (欧拉公式)b.中柔度杆：（直线公式） (说明：a 与b 与材料的性质有关的常数。

材质Q235B: a =304Mpa ; b =1.12 Mpa材质硬铝：a =372 Mpa ；b =2.14 Mpa )c.小柔度杆： A F s cr ⨯=σ8.计算：由压杆的约束条件选择相应的长度因素：因为后支撑的两端铰接，所以μ=1 压杆长度l=1325mm惯性半径 i=15.4mm由于斜支撑的材质：Q235B所以，弹性模量E=206GPa ；λ1=100 ；λ2=62柔度判定：因为λ 2 <λ<λ 1 ； 所以为中柔度杆因此，采用直线公式进行计算：F1=3702N ＜cr F N 61681=所以后支撑稳定。

864.1513251=⨯==i l μλ()()N A F cr 616811013.297108612.1304b λa 66=⨯⨯⨯⨯-=⨯-=-22)(l EI F cr μπ=()A F cr ⨯-=b λa。

第16章压杆稳定16.1 压杆稳定性的概念在第二章中，曾讨论过受压杆件的强度问题，并且认为只要压杆满足了强度条件，就能保证其正常工作。

但是，实践与理论证明，这个结论仅对短粗的压杆才是正确的，对细长压杆不能应用上述结论，因为细长压杆丧失工作能力的原因，不是因为强度不够，而是由于出现了与强度问题截然不同的另一种破坏形式，这就是本章将要讨论的压杆稳定性问题。

当短粗杆受压时(图16-1a)，在压力F由小逐渐增大的过程中，杆件始终保持原有的直线平衡形式，直到压力F达到屈服强度载荷F s(或抗压强度载荷F b)，杆件发生强度破坏时为止。

但是，如果用相同的材料，做一根与图16-1a所示的同样粗细而比较长的杆件(图16-1b)，当压力F比较小时，这一较长的杆件尚能保持直线的平衡形式，而当压力F逐渐增大至某—数值F1时，杆件将突然变弯，不再保持原有的直线平衡形式，因而丧失了承载能力。

我们把受压直杆突然变弯的现象，称为丧失稳定或失稳。

此时，F1可能远小于F s(或F b)。

可见，细长杆在尚未产生强度破坏时，就因失稳而破坏。

图16－1失稳现象并不限于压杆，例如狭长的矩形截面梁，在横向载荷作用下，会出现侧向弯曲和绕轴线的扭转(图16-2)；受外压作用的圆柱形薄壳，当外压过大时，其形状可能突然变成椭圆(图16-3)；圆环形拱受径向均布压力时，也可能产生失稳(图16-4)。

本章中，我们只研究受压杆件的稳定性。

图16-3所谓的稳定性是指杆件保持原有直线平衡形式的能力。

实际上它是指平衡状态的稳定性。

我们借助于刚性小球处于三种平衡状态的情况来形象地加以说明。

第一种状态，小球在凹面的O点处于平衡状态，如图16-5a所示。

先用外加干扰力使其偏离原有的平衡位置，然后再把干扰力去掉，小球能回到原来的平衡位置。

因此，小球原有的平衡状态是稳定平衡。

第二种状态，小球在凸面上的O点处于平衡状态，如图16-5c所示。

当用外加干扰力使其偏离原有的平衡位置后，小球将继续下滚，不再回到原来的平衡位置。

第五章轴心受力构件轴心受拉构件轴心受压构件强度（承载能力极限状态）刚度（正常使用极限状态）强度刚度（正常使用极限状态）稳定（承载能力极限状态）强度计算（承载能力极限状态）N —轴心拉力或压力设计值；A n —构件的净截面面积；f —钢材的抗拉强度设计值。

nN fA σ=≤轴心受压构件，当截面无削弱时，强度不必计算。

刚度计算（正常使用极限状态）截面的回转半径；−=AIi 0[]l iλλ=<构件的计算长度；−0l 取值详见规范或教材。

构件的容许长细比，其−][λ轴心受压构件的整体稳定计算N Afϕ≤N f Aϕ≤Nf Aϕ≤构件长细比的确定①、截面为双轴对称或极对称构件：xxy yyoy y x ox x i l i l ==λλ②、截面为单轴对称构件：xxy yx ox x i l x =λ轴：绕非对称轴绕对称轴y 轴屈曲时，一般为弯扭屈曲，其临界力低于弯曲屈曲，所以计算时，以换算长细比λyz 代替λyxx yy轴心受压构件的局部稳定()235100.1yb t f λ≤+btb翼缘板：腹板：t wh 0h 0t w()0235250.5w yh t f λ≤+式中：λ—取构件两方向长细比较大者，当λ<30,取λ=30；当λ>100，取λ=100工字型截面：翼缘板自由外伸宽度b的取值，GB50017规定：对焊接构件取腹板边缘至翼缘板自由端的距离；对轧制构件取内圆弧起点至翼缘板自由端的距离。

箱形截面翼缘板023540yb t f ≤箱形截面th 0t w箱形截面腹板023540w yh t f ≤与长细比无关格构式轴压构件设计1、强度fA N ≤=nσN —轴心压力设计值；A n —柱肢净截面面积之和。

y yxx实轴虚轴N（1）对实轴（y-y 轴）的整体稳定得。

并按相应的截面分类查由y y y f ANλϕϕ−≤y yxx实轴虚轴2、整体稳定验算（2）对虚轴（x-x ）稳定20127x xAA λλ=+得。

压杆的稳定计算—折减系数法一、稳定条件要使压杆不丧失稳定，应使作用在杆上的压力stcrn P P ≤P cr P st n st cr st cr n n P P σσ=⋅A ≤A =[]st A P σσ≤=AP=σ[]st cr st n σσ=cr σst n λ[]st σλ[]σ[]st σ[]σ[][]crst stn σσϕσ==[]σσϕ⋅=st crn []σϕ()10≤≤ϕϕλE ϕ[]σϕσ≤=Pϕ三、稳定计算应用（）式的稳定条件，可对压杆进行三种稳定方面的计算。

1稳定性校核按照压杆给定的支承情况确定μ值，然后由已知截面的形状和尺寸计算面积A 、惯性矩I 、惯性半径i 及柔度λ，由λ查表得出ϕ值，最后验算是否满足][σϕσ≤=AP这一稳定条件。

2确定许用荷载根据压杆的支承情况，截面形状和尺寸依次确定μ值、计算A 、I 、i 、λ各值。

然后根据材料和λ值，由表查出ϕ，最后按稳定条件计算许用荷载：[][]ϕσ⋅≤A P3选择截面稳定条件经变换后可得： []σϕpA ≥上式表明，要计算A ，先要查知ϕ，但ϕ与λ有关，λ与i 有关，i 与A 有关，当A 未求得之前，ϕ值也不能查出。

一般采用试算法。

例 图所示千斤顶的最大起重量kN P 120=。

已知丝杠的长度mm l 600=，mm h 100=，丝杠内径mm d 52=，丝杆材料为235Q 钢，[]MPa 80=σ，试校核丝杆的稳定性。

图解：（1）首先计算柔度丝杆可粗略地简化为下端固定、上端自由的压杆，故长度系数为2，丝杆的长度取最不利的状态为2h l -，则()62.84452506002=-⨯==ilμλ（2）查表并用内插法计算62.84=λ对应的ϕ值。

80=λ，731.0=ϕ；90=λ，669.0=ϕ任务实施PdhP62.84=λ时()702.08062.848090669.0731.0731.0=----=ϕ（3）校核丝杆稳定性[]MPa 19.5680702.0=⨯=σϕMPa AP 53.565241012023=⨯⨯==πσ[]σϕσ>，但没有超过5%，所以丝杆满足稳定性条件。