2017学年北京市昌平区临川学校七年级(上)数学期中试卷带参考答案

2016-2017学年北京市昌平区七年级（上）期末数学试卷一、选择题（本题共10道小题，每小题3分，共30分）下面各题均有四个选项，其中只有一个是符合题意的．1．﹣4的相反数是（）A．B．﹣ C．4 D．﹣42．计算﹣2×3结果正确的是（）A．6 B．﹣6 C．5 D．﹣53．昌平万亩滨河森林公园占地3 980 000平方米，位于北京城市中轴线的北延线上，将北京城与十三陵水库通过绿轴有机地联系在一起，是名副其实的北京的“后花园”．把数字3 980 000用科学记数法表示为（）A．39.8×105B．3.98×106C．3.98×107D．0.398×1074．数轴上有A，B，C，D四个点，其中绝对值相等的点是（）A．点A与点D B．点A与点C C．点B与点C D．点B与点D5．圆锥侧面展开图可能是下列图中的（）A．B．C．D．6．下列四个图形中，能用∠1，∠AOB，∠O三种方法表示同一个角的是（）A．B． C．D．7．将一副直角三角尺按如图所示摆放，图中锐角∠1的度数为（）A．58°B．59°C．60°D．61°8．如果代数式3x2﹣4x的值为6，那么6x2﹣8x﹣9的值为（）A．12 B．3 C．D．﹣39．如果|x﹣2|+（y+3）2=0，那么y x的值为（）A．9 B．﹣9 C．6 D．﹣610．按一定的规律排列的一列数依次为：﹣2，5，﹣10，17，﹣26，…，按此规律排列下去，这列数中第9个数及第n个数（n为正整数）分别是（）A．82，﹣n2+1 B．82，（﹣1）n（n2+1）C．﹣82，（﹣1）n（n2+1）D．﹣82，3n+1二、填空题（本题共6道小题，每小题3分，共18分）11．﹣3的倒数是．12．小莉在办板报时，需要画一条直的隔线，由于尺子不够长，于是她和一名同学找来一根线绳，给线绳涂上彩色粉笔沫，两人拉紧线绳各按住一头，把绳子从中间拉起再松手便完成了，请写出他们这样做根据的数学事实为．13．请写出一个次数为5的单项式．14．如果a，b互为相反数，c，d互为倒数，x的绝对值等于2，那么x2+cdx﹣a﹣b的值是．15．如图，将长和宽分别是a，b的长方形纸片的四个角都剪去一个边长为x的正方形．用含a，b，x的代数式表示纸片剩余部分的面积为．16．请写出解方程﹣=1的思路为．三、解答题（本题共7道小题，第17，18，19小题各3分；第20-23小题各4分，共25分）17．计算：﹣15﹣（﹣4）+1．18．计算：1+8÷（﹣2）×．19．计算：12×（﹣+）．20．计算：36÷（﹣3）2×（﹣）﹣（﹣12）．21．先化简，再求值：（﹣2ab+3a）﹣2（2a﹣b）+2ab，其中a=3，b=1．22．解方程：﹣3（2+x）=2（5﹣x）．23．解方程：=1+．四、解答题（本题共3道小题，每小题各4分，共12分）24．按照下列要求完成作图及问题解答．（1）分别作直线AB和射线AC；（2）作线段BC，取BC的中点D；（3）过点D作直线AB的垂线，交直线AB于点E；（4）测量点D到直线AB的距离为cm．25．列方程解应用题．为纪念红军长征胜利80周年，让人们更好地了解历史，开展爱国主义教育，传承和弘扬伟大的长征精神，军事博物馆举办“英雄史诗不朽丰碑﹣﹣纪念中国工农红军长征胜利80周年主题展览”．展览图片、文物、艺术品共计572件，文物比艺术品的5倍还多27件，图片比文物、艺术品的和少22件，求展出的艺术品有多少件．26．补全解题过程．已知：如图，点C是线段AB的中点，AD=6，BD=4，求CD的长．解：∵AD=6，BD=4，∴AB=AD+ =．∵点C是线段AB的中点，∴AC=CB==．∴CD=AD﹣=．五、解答题（本题共3道小题，每小题各5分，共15分）27．如图，数轴上点A对应的有理数为20，点P以每秒2个单位长度的速度从点A出发，点Q以每秒4个单位长度的速度从原点O出发，且P，Q两点同时向数轴正方向运动，设运动时间为t秒．（1）当t=2时，P，Q两点对应的有理数分别是，，PQ=；（2）当PQ=10时，求t的值．28．已知：如图，OA⊥OB，∠BOC=50°，且∠AOD：∠COD=4：7．画出∠BOC的角平分线OE，并求出∠DOE的度数．29．小聪和小敏在研究绝对值的问题时，遇到了这样一道题：当式子|x﹣1|+|x+5|取最小值时，x应满足的条件是，此时的最小值是．小聪说：利用数轴求线段的长可以解决这个问题．如图，点A，B对应的数分别为﹣5，1，则线段AB的长为6，我发现也可通过|1﹣（﹣5）|或|﹣5﹣1|来求线段AB的长，即数轴上两点间的线段的长等于它们所对应的两数差的绝对值．小敏说：我明白了，若点C在数轴上对应的数为x，线段AC的长就可表示为|x﹣（﹣5）|，那么|x﹣1|表示的是线段的长．小聪说：对，求式子|x﹣1|+|x+5|的最小值就转化为数轴上求线段AC+BC长的最小值，而点C在线段AB上时AC+BC=AB最小，最小值为6．小敏说：点C在线段AB上，即x取﹣5，1之间的有理数（包括﹣5，1），因此相应x的取值范围可表示为﹣5≤x≤1时，最小值为6．请你根据他们的方法解决下面的问题：（1）小敏说的|x﹣1|表示的是线段的长；（2）当式子|x﹣3|+|x+2|取最小值时，x应满足的条件是；（3）当式子|x﹣2|+|x+3|+|x+4|取最小值时，x应满足的条件是；（4）当式子|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|（a＜b＜c＜d）取最小值时，x应满足的条件是，此时的最小值是．2016-2017学年北京市昌平区七年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共10道小题，每小题3分，共30分）下面各题均有四个选项，其中只有一个是符合题意的．1．﹣4的相反数是（）A．B．﹣ C．4 D．﹣4【考点】相反数．【分析】根据相反数的定义作答即可．【解答】解：﹣4的相反数是4．故选C．2．计算﹣2×3结果正确的是（）A．6 B．﹣6 C．5 D．﹣5【考点】有理数的乘法．【分析】根据有理数的乘法法则计算即可．【解答】解：﹣2×3=﹣6，故选B3．昌平万亩滨河森林公园占地3 980 000平方米，位于北京城市中轴线的北延线上，将北京城与十三陵水库通过绿轴有机地联系在一起，是名副其实的北京的“后花园”．把数字3 980 000用科学记数法表示为（）A．39.8×105B．3.98×106C．3.98×107D．0.398×107【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：把数字3 980 000用科学记数法表示为3.98×106，故选：B．4．数轴上有A，B，C，D四个点，其中绝对值相等的点是（）A．点A与点D B．点A与点C C．点B与点C D．点B与点D【考点】数轴；绝对值．【分析】根据数轴上绝对值相等的点到原点的距离相等，判断出数轴上有A，B，C，D四个点，其中绝对值相等的点是哪两个点即可．【解答】解：∵点B与点C到原点的距离相等，∴数轴上有A，B，C，D四个点，其中绝对值相等的点是点B与点C．故选：C．5．圆锥侧面展开图可能是下列图中的（）A．B．C．D．【考点】几何体的展开图．【分析】直接利用圆锥侧面展开图形状判断得出答案．【解答】解：圆锥的侧面展开图是扇形．故选：D．6．下列四个图形中，能用∠1，∠AOB，∠O三种方法表示同一个角的是（）A．B． C．D．【考点】角的概念．【分析】根据角的表示方法进行逐一分析，即角可以用一个大写字母表示，也可以用三个大写字母表示．其中顶点字母要写在中间，唯有在顶点处只有一个角的情况，才可用顶点处的一个字母来记这个角，否则分不清这个字母究竟表示哪个角．角还可以用一个希腊字母（如∠α，∠β，∠γ、…）表示，或用阿拉伯数字（∠1，∠2…）表示．【解答】解：A、因为顶点O处有四个角，所以这四个角均不能用∠O表示，故本选项错误；B、因为顶点O处只有一个角，所以这个角能用∠1，∠AOB，∠O表示，故本选项正确；C、因为顶点O处有三个角，所以这三个角均不能用∠O表示，故本选项错误；D、因为顶点O处有三个角，所以这三个角均不能用∠O表示，故本选项错误．故选B．7．将一副直角三角尺按如图所示摆放，图中锐角∠1的度数为（）A．58°B．59°C．60°D．61°【考点】余角和补角．【分析】根据三角尺上的度数用90°减去30°即可求解．【解答】解：锐角∠1的度数为90°﹣30°=60°．故选：C．8．如果代数式3x2﹣4x的值为6，那么6x2﹣8x﹣9的值为（）A．12 B．3 C．D．﹣3【考点】代数式求值．【分析】首先依据等式的性质求得6x2﹣8x的值，然后代入求解即可．【解答】解：∵3x2﹣4x=6，∴6x2﹣8x=12．∴6x2﹣8x﹣9=12﹣9=3．故选：B．9．如果|x﹣2|+（y+3）2=0，那么y x的值为（）A．9 B．﹣9 C．6 D．﹣6【考点】代数式求值；非负数的性质：绝对值；非负数的性质：偶次方．【分析】首先依据非负数的性质求得x、y的值，然后代入计算即可．【解答】解：∵|x﹣2|+（y+3）2=0，∴x=2，y=﹣3．∴原式=（﹣3）2=9．故选：A．10．按一定的规律排列的一列数依次为：﹣2，5，﹣10，17，﹣26，…，按此规律排列下去，这列数中第9个数及第n个数（n为正整数）分别是（）A．82，﹣n2+1 B．82，（﹣1）n（n2+1）C．﹣82，（﹣1）n（n2+1）D．﹣82，3n+1【考点】规律型：数字的变化类．【分析】从数的变化，可以先考虑它们的绝对值的变化规律，为n2+1，然后每隔一个数为负数，最后归纳第n个数即（﹣1）n（n2+1）．【解答】解：根据数值的变化规律可得：第一个数：﹣2=（﹣1）1（12+1）．第二个数：5=（﹣1）2（22+1）．第三个数：﹣10=（﹣1）3（32+1）．∴第9个数为：（﹣1）9（92+1）=﹣82第n个数为：（﹣1）n（n2+1）．故选择C．二、填空题（本题共6道小题，每小题3分，共18分）11．﹣3的倒数是﹣．【考点】倒数．【分析】根据倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．【解答】解：﹣3的倒数是﹣．12．小莉在办板报时，需要画一条直的隔线，由于尺子不够长，于是她和一名同学找来一根线绳，给线绳涂上彩色粉笔沫，两人拉紧线绳各按住一头，把绳子从中间拉起再松手便完成了，请写出他们这样做根据的数学事实为两点确定一条直线．【考点】直线的性质：两点确定一条直线．【分析】直接利用直线的性质分析得出答案．【解答】解：小莉在办板报时，需要画一条直的隔线，由于尺子不够长，于是她和一名同学找来一根线绳，给线绳涂上彩色粉笔沫，两人拉紧线绳各按住一头，把绳子从中间拉起再松手便完成了，他们这样做根据的数学事实为：两点确定一条直线．故答案为：两点确定一条直线．13．请写出一个次数为5的单项式x5（不唯一）．【考点】单项式．【分析】单项式的次数是指单项式中所有字母因数的指数和；所以4x5，x4y，3y5等都是五次单项式．答案不唯一．【解答】解：一个次数为5的单项式x5（不唯一）．故答案为：x5（不唯一）．14．如果a，b互为相反数，c，d互为倒数，x的绝对值等于2，那么x2+cdx﹣a﹣b的值是6或2．【考点】代数式求值．【分析】依据相反数、倒数、绝对值的性质求得a+b=0，cd=1，x=±2，然后代入计算即可．【解答】解：∵a，b互为相反数，c，d互为倒数，x的绝对值等于2，∴a+b=0，cd=1，x=±2．当x=2时，原式=4+2﹣0=6；当x=﹣2时，原式=4﹣2﹣0=2．故答案为：6或2．15．如图，将长和宽分别是a，b的长方形纸片的四个角都剪去一个边长为x的正方形．用含a，b，x的代数式表示纸片剩余部分的面积为ab﹣4x2．【考点】列代数式．【分析】根据题意和图形可以用相应的代数式表示出纸片剩余部分的面积．【解答】解：由图可得，纸片剩余部分的面积为：ab﹣4x2，故答案为：ab﹣4x2．16．请写出解方程﹣=1的思路为化小数系数为整数系数，去分母、去括号、移项、合并同类项、系数化为1．【考点】解一元一次方程．【分析】根据“化小数系数为整数系数，去分母、去括号、移项、合并同类项、系数化为1”即可求解．【解答】解：方程整理得：﹣=1，去分母得：20x﹣4﹣15+30=6，移项合并得：20x=﹣5，解得：x=﹣0.25．则解方程的思路为化小数系数为整数系数，去分母、去括号、移项、合并同类项、系数化为1，故答案为：化小数系数为整数系数，去分母、去括号、移项、合并同类项、系数化为1三、解答题（本题共7道小题，第17，18，19小题各3分；第20-23小题各4分，共25分）17．计算：﹣15﹣（﹣4）+1．【考点】有理数的加减混合运算．【分析】有理数的加减法，从左往右依次计算．【解答】解：原式=﹣15+4+1=﹣15+5=﹣10．18．计算：1+8÷（﹣2）×．【考点】有理数的混合运算．【分析】原式先计算乘除运算，再计算加减运算即可得到结果．【解答】解：原式=1+（﹣4）×=1﹣2=﹣1．19．计算：12×（﹣+）．【考点】有理数的混合运算．【分析】原式利用乘法分配律计算即可得到结果．【解答】解：原式=6﹣8+9=7．20．计算：36÷（﹣3）2×（﹣）﹣（﹣12）．【考点】有理数的混合运算．【分析】原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．【解答】解：原式=36÷9×（﹣）﹣（﹣1）=4×（﹣）+1=﹣1+1=0．21．先化简，再求值：（﹣2ab+3a）﹣2（2a﹣b）+2ab，其中a=3，b=1．【考点】整式的加减—化简求值．【分析】原式去括号合并得到最简结果，把a与b的值代入计算即可求出值．【解答】解：原式=﹣2ab+3a﹣4a+2b+2ab=﹣a+2b，当a=3，b=1时，原式=﹣3+2=﹣1．22．解方程：﹣3（2+x）=2（5﹣x）．【考点】解一元一次方程．【分析】方程去括号，移项合并，把x系数化为1，即可求出解．【解答】解：去括号得：﹣6﹣3x=10﹣2x，移项得：﹣3x+2x=10+6，合并得：﹣x=16，解得：x=﹣16．23．解方程：=1+．【考点】解一元一次方程．【分析】方程去分母，去括号，移项合并，把x系数化为1，即可求出解．【解答】解：去分母得：（5x﹣3）=4+2（x+1），去括号得：5x﹣3=4+2x+2，移项得：5x﹣2x=4+2+3，合并得：3x=9，解得：x=3．四、解答题（本题共3道小题，每小题各4分，共12分）24．按照下列要求完成作图及问题解答．（1）分别作直线AB和射线AC；（2）作线段BC，取BC的中点D；（3）过点D作直线AB的垂线，交直线AB于点E；（4）测量点D到直线AB的距离为1cm．【考点】作图—复杂作图．【分析】（1）分别作直线AB和射线AC；（2）作线段BC，取BC的中点D；（3）过点D作直线AB的垂线，交直线AB于点E；（4）测量点D到直线AB的距离即可．【解答】解：（1）如图，分别作直线AB和射线AC；（2）如图，作线段BC，取BC的中点D；（3）如图，过点D做直线AB的垂线，交直线AB于点E；（4）经测量，点D到直线AB的距离约1cm．25．列方程解应用题．为纪念红军长征胜利80周年，让人们更好地了解历史，开展爱国主义教育，传承和弘扬伟大的长征精神，军事博物馆举办“英雄史诗不朽丰碑﹣﹣纪念中国工农红军长征胜利80周年主题展览”．展览图片、文物、艺术品共计572件，文物比艺术品的5倍还多27件，图片比文物、艺术品的和少22件，求展出的艺术品有多少件．【考点】一元一次方程的应用．【分析】设展出的艺术品有x件，根据展览图片+文物+艺术品=572件和文物比艺术品的5倍还多27件，图片比文物、艺术品的和少22件，列出方程求解即可．【解答】解：设展出的艺术品有x件，根据题意列方程，得（5x+27+x﹣22）+x+（5x+27）=572，解得：x=45．答：展出的艺术品有45件．26．补全解题过程．已知：如图，点C是线段AB的中点，AD=6，BD=4，求CD的长．解：∵AD=6，BD=4，∴AB=AD+ BD=10．∵点C是线段AB的中点，∴AC=CB=AB=5．∴CD=AD﹣AC=1．【考点】两点间的距离．【分析】根据线段的和差，可得AB的长，根据线段中点的性质，可得AC的长，再根据线段的和差，可得答案．【解答】解：：∵AD=6，BD=4，∴AB=AD+BD=10．∵点C是线段AB的中点，∴AC=CB=AB=5．∴CD=AD﹣AC=1．故答案为：BD，10；AB，5；AC，1．五、解答题（本题共3道小题，每小题各5分，共15分）27．如图，数轴上点A对应的有理数为20，点P以每秒2个单位长度的速度从点A出发，点Q以每秒4个单位长度的速度从原点O出发，且P，Q两点同时向数轴正方向运动，设运动时间为t秒．（1）当t=2时，P，Q两点对应的有理数分别是24，8，PQ=16；（2）当PQ=10时，求t的值．【考点】一元一次方程的应用；数轴；代数式求值．【分析】（1）根据点P、Q的运动方向、速度和时间，即可得出当t=2时，P、Q两点对应的有理数，二者做差即可求出线段PQ的长度；（2）分点P在点Q右侧和点P在点Q左侧两种情况考虑，根据PQ=10结合运动时间为t 时P、Q两点对应的有理数，即可列出关于t的一元一次方程，解之即可得出结论．【解答】解：（1）∵20+2×2=24，4×2=8，∴当t=2时，P，Q两点对应的有理数分别是24，8，∴PQ=24﹣8=16．故答案为：24；8；16．（2）①当点P在点Q右侧时，PQ=（20+2t）﹣4t=10，解得：t=5；②当点P在点Q左侧时，PQ=4t﹣（20+2t）=10，解得：t=15．综上所述，t的值为5秒或15秒．28．已知：如图，OA⊥OB，∠BOC=50°，且∠AOD：∠COD=4：7．画出∠BOC的角平分线OE，并求出∠DOE的度数．【考点】垂线；角平分线的定义；角的计算．【分析】设∠AOD=4x，∠COD=7x，根据题意列出方程即可求得∠COD=140°，然后根据角平分线的定义计算∠COE的度数，最后结合图形计算∠DOE的度数．【解答】解：（1）如右图：（2）∵OA⊥OB，∴∠AOB=90°，∵∠AOD：∠COD=4：7，∴设∠AOD=4x°，∠COD=7x°，∵∠AOB+∠AOD+∠COD+∠BOC=360°，且∠BOC=50°，∴90+7x+4x+50=360，∴x=20，∴∠COD=140°．∵OE是∠BOC的角平分线，∴∠BOC=25°，∴∠DOE=∠COD+∠COE=165°，29．小聪和小敏在研究绝对值的问题时，遇到了这样一道题：当式子|x﹣1|+|x+5|取最小值时，x应满足的条件是﹣5≤x≤1，此时的最小值是6．小聪说：利用数轴求线段的长可以解决这个问题．如图，点A，B对应的数分别为﹣5，1，则线段AB的长为6，我发现也可通过|1﹣（﹣5）|或|﹣5﹣1|来求线段AB的长，即数轴上两点间的线段的长等于它们所对应的两数差的绝对值．小敏说：我明白了，若点C在数轴上对应的数为x，线段AC的长就可表示为|x﹣（﹣5）|，那么|x﹣1|表示的是线段BC的长．小聪说：对，求式子|x﹣1|+|x+5|的最小值就转化为数轴上求线段AC+BC长的最小值，而点C在线段AB上时AC+BC=AB最小，最小值为6．小敏说：点C在线段AB上，即x取﹣5，1之间的有理数（包括﹣5，1），因此相应x的取值范围可表示为﹣5≤x≤1时，最小值为6．请你根据他们的方法解决下面的问题：（1）小敏说的|x﹣1|表示的是线段BC的长；（2）当式子|x﹣3|+|x+2|取最小值时，x应满足的条件是﹣2≤x≤3；（3）当式子|x﹣2|+|x+3|+|x+4|取最小值时，x应满足的条件是x=﹣3；（4）当式子|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|（a＜b＜c＜d）取最小值时，x应满足的条件是b≤x≤c，此时的最小值是c﹣b+d﹣a．【考点】整式的加减；数轴；绝对值．【分析】根据绝对值的性质以及题意即可求出答案．【解答】解：（1）由题意可知：|x﹣1|=BC；（2）由题意可知：﹣2≤x≤3；（3）|x﹣2|+|x+3|+|x+4|表示数x分别与﹣4、﹣3、2的距离之和，由题意可知：当﹣3≤x≤2时，|x+3|+|x﹣2|可取得最小值，∴当x=﹣3时，|x﹣2|+|x+3|+|x+4|可取得最小值，（4）由题意可知：|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|表示数x分别与a、b、c、d的距离之和，∴b≤x≤c时，x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|的最小值为：c﹣b+d﹣a．故答案为：﹣5≤x≤1，6（1）BC（2）﹣2≤x≤3（3）x=﹣3（4）b≤x≤c，c﹣b+d﹣a．2017年3月17日。

北京市昌平临川育人学校2017-2018学年七年级数学下学期期中试题（B卷）一、选择题（每小题2分，共计20分） 1.下列计算正确的是（ ）A. 248a a a =÷B. 532x x x =+C.853)()(c c c =-∙-D.22))((y x y x y x +-=+---2. H7N9禽流感病毒的直径大约是0.000000081米，用科学记数法可表示为（ ）A. 8.1×10-9米 B. 8.1×10-8米 C. 81×10-9米 D. 0.81×10-7米 3. 单项式A 与-3x 2y 的乘积是6x 6y 2，则单项式A 是（ ）A. 2x 3y B. -2x 3y C. -2x 4y D. 2x 4y 4．尺规作图所用的作图工具是指( )． A ．刻度尺和圆规 B ．不带刻度的直尺和圆规 C ．刻度尺D ．圆规5．下列语句不正确的是 A ．对顶角相等 B ．两点之间线段最短 C ．同旁内角互补D ．延长线段AB 到C6. 如图,1∠与2∠是对顶角的是7．计算：3－2的结果是( )． A ．－9 B ．－6 C ．－19 D.198. 已知：如图AB ∥CD ，CE 平分∠ACD ，∠A=110°，则∠ECD 等于A.110°B.70°C.55°D.35°9.骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，因变量是（ ）A 、沙漠B 、体温C 、时间D 、骆驼10．如图，E 为BC 上一点，AB ∥C D∥EF ，AE ∥CG ，则图中与∠A （不包括∠A ）相等的角有CA BED第8题图A ．5个B ．4个C ．3个D ．2个二、填空题（每小题2分，共20分）11.如图，写一个使AB ∥CD 的条件 。

12. 若a m=2，a n=4，则a m-n=________.13. 计算：（9a 2b-6ab 2）÷（3ab ）= .14.在“变量之间的关系”一章中，我们学习的“变量”是指自变量和因变量，而表达它们之间的关系通常有三种方法，这三种方法是指 、 和 ．15．两条直线相交所成的四个角中，有一组邻补角相等时，这两条直线的位置关系是____． 16．PM 2.5即细颗粒物，指环境空气中直径小于等于 0.0000025 米的颗粒物，这个数据用科学记数法表示为___________________.17．如图，用量角器量一个破损的扇形零件的圆心角，请写出这个圆心角的度数是______，根据是_______________________________.18．16.若622=-n m ，且3=-n m ，则=+n m ．19、平行线的性质： 平行线的判定：（1）两直线平行， ；（4） ，两直线平行； （2）两直线平行， ；（5） ，两直线平行； （3）两直线平行， ；（6） ，两直线平行。

2016-2017学年北京市昌平区七年级（上）期末数学试卷（删减版）参考答案与试题解析一、选择题（本题共10道小题，每小题3分，共30分）下面各题均有四个选项，其中只有一个是符合题意的．1．（3分）﹣4的相反数是（）A．B．﹣C．4D．﹣4【解答】解：﹣4的相反数是4．故选C．2．（3分）计算﹣2×3结果正确的是（）A．6B．﹣6C．5D．﹣5【解答】解：﹣2×3=﹣6，故选B3．（3分）昌平万亩滨河森林公园占地3980000平方米，位于北京城市中轴线的北延线上，将北京城与十三陵水库通过绿轴有机地联系在一起，是名副其实的北京的“后花园”．把数字3980000用科学记数法表示为（）A．39.8×105B．3.98×106C．3.98×107D．0.398×107【解答】解：把数字3980000用科学记数法表示为3.98×106，故选：B．4．（3分）数轴上有A，B，C，D四个点，其中绝对值相等的点是（）A．点A与点D B．点A与点C C．点B与点C D．点B与点D【解答】解：∵点B与点C到原点的距离相等，∴数轴上有A，B，C，D四个点，其中绝对值相等的点是点B与点C．故选：C．5．（3分）圆锥侧面展开图可能是下列图中的（）A．B．C．D．【解答】解：圆锥的侧面展开图是扇形．故选：D．8．（3分）如果代数式3x2﹣4x的值为6，那么6x2﹣8x﹣9的值为（）A．12B．3C．D．﹣3【解答】解：∵3x2﹣4x=6，∴6x2﹣8x=12．∴6x2﹣8x﹣9=12﹣9=3．故选：B．9．（3分）如果|x﹣2|+（y+3）2=0，那么y x的值为（）A．9B．﹣9C．6D．﹣6【解答】解：∵|x﹣2|+（y+3）2=0，∴x=2，y=﹣3．∴原式=（﹣3）2=9．故选：A．10．（3分）按一定的规律排列的一列数依次为：﹣2，5，﹣10，17，﹣26，…，按此规律排列下去，这列数中第9个数及第n个数（n为正整数）分别是（）A．82，﹣n2+1B．82，（﹣1）n（n2+1）C．﹣82，（﹣1）n（n2+1）D．﹣82，3n+1【解答】第一个数：﹣2=（﹣1）1（12+1）．第二个数：5=（﹣1）2（22+1）．第三个数：﹣10=（﹣1）3（32+1）．∴第9个数为：（﹣1）9（92+1）=﹣82第n个数为：（﹣1）n（n2+1）．故选择C．二、填空题（本题共6道小题，每小题3分，共18分）11．（3分）﹣3的倒数是﹣．15．（3分）如图，将长和宽分别是a，b的长方形纸片的四个角都剪去一个边长为x的正方形．用含a，b，x的代数式表示纸片剩余部分的面积为ab﹣4x2．【解答】解：由图可得，19．（3分）计算：12×（﹣+）．【解答】解：原式=6﹣8+9=7．20．（4分）计算：36÷（﹣3）2×（﹣）﹣（﹣12）．【解答】解：原式=36÷9×（﹣）﹣（﹣1）=4×（﹣）+1=﹣1+1=0．21．（4分）先化简，再求值：（﹣2ab+3a）﹣2（2a﹣b）+2ab，其中a=3，b=1．【解答】解：原式=﹣2ab+3a﹣4a+2b+2ab=﹣a+2b，当a=3，b=1时，原式=﹣3+2=﹣1．22．（4分）解方程：﹣3（2+x）=2（5﹣x）．【解答】解：去括号得：﹣6﹣3x=10﹣2x，移项得：﹣3x+2x=10+6，合并得：﹣x=16，解得：x=﹣16．23．（4分）解方程：=1+．【解答】解：去分母得：（5x﹣3）=4+2（x+1），去括号得：5x﹣3=4+2x+2，移项得：5x﹣2x=4+2+3，合并得：3x=9，解得：x=3．四、解答题（本题共3道小题，每小题各4分，共12分）24．（4分）按照下列要求完成作图及问题解答．（1）分别作直线AB和射线AC；（2）作线段BC，取BC的中点D；（3）过点D作直线AB的垂线，交直线AB于点E；（4）测量点D到直线AB的距离为1cm．【解答】解：（1）如图，分别作直线AB和射线AC；（2）如图，作线段BC，取BC的中点D；（3）如图，过点D做直线AB的垂线，交直线AB于点E；（4）经测量，点D到直线AB的距离约1cm．25．（4分）列方程解应用题．为纪念红军长征胜利80周年，让人们更好地了解历史，开展爱国主义教育，传承和弘扬伟大的长征精神，军事博物馆举办“英雄史诗不朽丰碑﹣﹣纪念中国工农红军长征胜利80周年主题展览”．展览图片、文物、艺术品共计572件，文物比艺术品的5倍还多27件，图片比文物、艺术品的和少22件，求展出的艺术品有多少件．【解答】解：设展出的艺术品有x件，根据题意列方程，得（5x+27+x﹣22）+x+（5x+27）=572，解得：x=45．答：展出的艺术品有45件．26．（4分）补全解题过程．已知：如图，点C是线段AB的中点，AD=6，BD=4，求CD的长．解：∵AD=6，BD=4，∴AB=AD+BD=10．∵点C是线段AB的中点，∴AC=CB=AB=5．∴CD=AD﹣AC=1．【解答】解：：∵AD=6，BD=4，∴AB=AD+BD=10．∵点C是线段AB的中点，∴∴27Q t（1（2∴（2PQ=综上所述，t的值为5秒或15秒．29．（5分）小聪和小敏在研究绝对值的问题时，遇到了这样一道题：当式子|x﹣1|+|x+5|取最小值时，x应满足的条件是﹣5≤x≤1，此时的最小值是6．小聪说：利用数轴求线段的长可以解决这个问题．如图，点A，B对应的数分别为﹣5，1，则线段AB 的长为6，我发现也可通过|1﹣（﹣5）|或|﹣5﹣1|来求线段AB的长，即数轴上两点间的线段的长等于它们所对应的两数差的绝对值．﹣1AB（1（2（3（4（2（3（4∴b（1（2（3）x=﹣3（4）b≤x≤c，c﹣b+d﹣a．。

北京市北京临川育人学校2017-2018学年七年级上学期第一次月考数学试题一、选择题（每题3分，共36分）1. 下表是我国几个城市某年一月份的平均气温，其中气温最低的城市是（）A. 哈尔滨B. 广州C. 武汉D. 北京【答案】A【解析】【分析】0℃以下记为负数，0℃以上记为正数，温度都小于0℃时，绝对值最大的，温度最低.【详解】广东和武汉温度高于0℃，北京和哈尔滨温度低于0℃，又哈尔滨的温度的绝对值大，所以答案选择A项.【点睛】本题考查了温度的比较以及正负数的概念，熟悉掌握概念是解决本题的关键.2. 下面的两个数中互为相反数的是（）A.12-和0.2 B.13和0.333- C. 5和(5)-- D. 2.25-和94【答案】D【解析】【分析】根据相反数的定义求解即可.【详解】只有符号不同的两个数互为相反数，A，B，C均不符合题意，而92.254=，所以 2.25-和94是相反数，故选D．【点睛】本题考查相反数，熟练掌握相反数的定义是解题关键.3. 两个负数的和一定是（ ）A. 负数B. 非正数C. 非负数D. 正数 【答案】A【解析】试题解析：两个负数的和一定是负数.故选A.4. ﹣3的相反数是（ ） A. 13- B. 13 C. 3- D. 3【答案】D【解析】【分析】相反数的定义是：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，0的相反数还是0．【详解】根据相反数的定义可得：－3的相反数是3.故选D.【点睛】本题考查相反数，题目简单，熟记定义是关键.5. 若x ＞0，y ＜0，且|x|＜|y |，则x ＋y 一定是（ ）A. 负数B. 正数C. 0D. 无法确定符号 【答案】A【解析】试题解析：00,.x y x y ><，＜0.x y ∴+<故选A.点睛：异号两数相加，去绝对值较大的数的正负号，并用较大数的绝对值减去较小数的绝对值.6. 一个数的绝对值是3，则这个数可以是（ ）A. 3B. 3-C. 3或者3-D. 13【答案】C【解析】试题解析：∵一个数的绝对值是3，可设这个数位a ，∴|a|=3，∴a=±3 故选C ．7. 下列说法：①若a 、b 互为相反数，则a +b =0；②若a +b =0，则a 、b 互为相反数；③若a 、b 互为相反数，则1a b =-；④若1a b=-，则a 、b 互为相反数.其中正确的结论是（ ）． A. ②③④B. ①②③C. ①②④D. ①② 【答案】C【解析】试题分析：根据相反数的定义逐一分析即可得出答案．解：∵互为相反数的两个数的和为0，又∵a 、b 互为相反数，∴a +b =0，反之也成立，故①、②正确；∵0的相反数是0，∴若a =b =0时，a b 无意义，故③错误； ∵a b=−1， ∴a =−b ，∴a 、b 互为相反数，故④正确；正确的有①②④.故选C.8. 温度升高50C ，再升高－50C ，结果是（ ） A. 温度升高了100CB. 温度下降了50CC. 温度不变D. 温度下降了100C【答案】C【解析】 试题分析：在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示，即得结果．若温度升高为正，则温度降低为负，则温度升高5℃，再升高-5℃，即温度先升高5℃，然后降低5℃，结果温度不变，故选C．考点：本题考查的是正数和负数点评：解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．9. 下列说法中，正确的是（）．A. 正整数和负整数统称整数B. 整数和分数统称有理数C. 零既可以是正整数，也可以是负整数D. 一个有理数不是正数就是负数【答案】B【解析】【分析】此题可根据有理数的意义对每个选项注意推理论证，得出正确选项．【详解】解：A、正整数和负整数统称整数，因为0是整数但既不是正数也不是负数，所以本选项错误；B、整数数和分数统称为有理数，此选项符合有理数的意义，所以本选项正确；C、零既可以是正数，也可以是负数，在有理数中，0既不是正数，也不是负数，所以本选项错误；D、0是有理数，但既不是正数也不是负数，所以本选项错误．故选B．【点睛】此题考查的知识点是有理数，关键是根据有理数其意义解答，重点掌握0既不是正数也不是负数，0是整数．10. 如图，是一台数值转换机，若输入的值为－5，则输出的结果为（）A. 11B. －9C. －17D. 21【答案】D【解析】 试题分析：根据题意可得：[(－5)－2]×(－3)=(－7)×(－3)=21.考点：有理数的计算11. 对于(－2)4与－24，下列说法正确的是( ) A. 它们的意义相同B. 它的结果相等C. 它的意义不同，结果相等D. 它的意义不同，结果不等【答案】D【解析】 试题分析：4(2)-的底数是﹣2，指数是4，结果是16；42-的底数是2，指数是4，它的意思是2的四次方的相反数，结果是﹣16．故选D ．考点：有理数的乘方．12. a 、b 、c 为非零有理数，它们的积必为正数的是（ ）A. 0a >，b 、c 同号B. 0b >，a 、c 异号C. 0c >，a 、b 异号D. a 、b 、c 同号 【答案】A【解析】 ,b c ∵异号，0.bc ∴>0.a >0.abc ∴>故选A.点睛：两数相乘，同号为正，异号为负.二、填空题（每题2分，共24分）13. ﹣25的绝对值是__，﹣25的相反数是__，﹣25的倒数是__． 【答案】 (1). 25 (2). 25 (3). 52 【解析】试题解析：25-的绝对值是2.5 25-的相反数是2.5 25-的倒数是5.2- 故答案为2,52,55.2- 点睛：只有符号不同的两个数互为相反数.乘积为1的两个数互为倒数.绝对值是指一个数在数轴上所对应的点到原点的距离.14. 某水库的水位下降1米，记作﹣1米，那么+1.2米表示_____．【答案】水位上升1.2米【解析】水库的水位下降1米，记作1-米，那么 1.2＋米表示水位上升1.2米.故答案为水位上升1.2米.15. 数轴上表示有理数-3.5与4.5两点的距离是___________.【答案】8【解析】试题分析：有理数-3.5与4.5两点的距离实为两数差的绝对值．解：由题意得：有理数−3.5与4.5两点的距离为|−3.5−4.5|=8.故答案为8.16. 最小的正整数和最大的负整数的和是_________ .【答案】0【解析】∵最大的负整数是1-，最小的正整数是1，而110-+=，∴最大的负整数与最小的正整数的和是0.17. 一天早晨的气温是－5℃，中午又上升了10℃，半夜又下降了8℃，则半夜的气温是________.【答案】－3℃【解析】气温上升为正，下降为负，列出算式求解即可.解：根据题意列示为：-5+10-8=-13+10= -3℃.故应填-3.“点睛”本题主要考查用正负来表示具有相反数的量，做题时一定要注意单位.18. 用“＜”“=”或“＞”号填空：﹣2 0，﹣ ﹣，﹣（+5） ﹣（﹣|﹣5|）． 【答案】＜；＞；＜【解析】试题分析：根据两个负数相比较，绝对值大的反而小，对每一组数计算后再判断大小．解：∵负数小于0，∴﹣2＜0；∵=，=， ∴＜，∴﹣＞﹣； ∵﹣（+5）=﹣5，﹣（﹣|﹣5|）=﹣（﹣5）=5，∴﹣（+5）＜﹣（﹣|﹣5|）． 故应填：＜；＞；＜．考点：有理数大小比较．19. 规定a*b=5a+2b-1，则（﹣4）*6的值为_______．【答案】-9【解析】【分析】根据a*b=5a+2b-1，可以求得题目中所求式子的值，本题得以解决．【详解】∵a*b=5a+2b-1，∴（-4）*6=5×（-4）+2×6-1=（-20）+12-1=-9，故答案为-9．【点睛】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．20. 绝对值小于4的所有整数的和是___________．【答案】0【解析】【分析】【详解】解：绝对值小于4的所有整数有：-3、-2、-1、0、1、2、3，（-3）+（-2）+（-1）+0+1+2+3=0，故答案为：0.21. 测得某乒乓球厂生产的五个乒乓球的质量误差（g）如下表．检验时，通常把比标准质量大的克数记为正，比标准质量小的克数记为负．请你选出最接近标准的球，是_______________号．【答案】1【解析】【分析】将五个球的误差绝对值按从小到大的顺序排列，找出误差绝对值最小的球即是所求．【详解】解：∵|-0.02|＜0.1＜0.2＜|-0.23|＜|-0.3|，∴1号球为最接近标准质量的球．故答案为：1．【点睛】本题考查了正数和负数以及绝对值，找出误差绝对值最小的球是解题的关键．22. 某次数学测验共20道选择题，规则是：选对一道得5分，选错一道得－1分，不选得零分，王明同学的卷面成绩是：选对16道题，选错2道题，有2道题未做，他的得分是_________.【答案】78分【解析】分析：根据规则列出得分的代数式计算即可．详解：∵选对一道得5分，选错一道得﹣1分，不选得零分，∴他的得分是：16×5﹣2=78．故答案为78．点睛：解答本题的关键是读懂题意，列式计算．23. 讲究卫生要勤洗手，人的一只手上大约有28 000万个看不见的细菌，用科学记数法表示一只手上大约有______个细菌.【答案】82.810【解析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．解：将28000万用科学记数法表示为2.8×108．故答案为2.8×108． 24. 某年级举办足球循环赛，规则是：胜一场得3分，平一场得1分，输一场得－1分．某班的比赛结果是胜3场、平2场、输4场，则该班得________分．【答案】7【解析】分析：足球循环赛，规则是：胜一场得+3分，平一场得+1分，输一场得﹣1分，根据题意可列算式计算．详解：根据题意可列算式为：3×3+2×1+4×（﹣1）=9+2﹣4=7，即该班得7分．故答案为7.点睛：本题主要考查正负数在实际生活中的应用，所以学生在学这一部分时一定要联系实际，不能死学．三、计算题（每题2分，共24分）25. (–1.1)+(–3.9);【答案】-5【解析】试题解析：()()()–1.1?3.9 1.1 3.9 5.+=-+=-点睛：同号两数相加，去相同的正负号，并把绝对值相加.26. +15+ (+6);【答案】21【解析】试题解析：()()15?61562121.+++=++=+=27. (+15)+(–6);【答案】9【解析】试题解析：()()156(156)99.++-=+-=+=28. 23－|－6|－（+23）【答案】-6【解析】试题解析：236(23)23623 6.---+=--=-29. 23－17－(－7)+(－16)【答案】-3【解析】试题解析：()2317(7)16231771667161316 3.---+-=-+-=+-=-=-点睛：根据有理数的混合运算的运算顺序和法则进行计算即可. 30. 157()(36)2912-+⨯-. 【答案】-19【解析】试题解析：()15736,2912⎛⎫-+⨯- ⎪⎝⎭()()()157363636,2912⎛⎫=⨯-+-⨯-+⨯- ⎪⎝⎭ ()182021,=-++-221,=-19.=- 31. 2112524⎡⎤⎛⎫⎛⎫⨯÷⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦－－－； 【答案】-3【解析】试题解析：2112524－－⎡⎤⎛⎫⎛⎫⨯-÷⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦ ()12544⎛⎫=⨯⨯- ⎪⎝⎭－ ()344=⨯- 3.=- 32. 1551121()2()1277225⨯--⨯+-÷ ； 【答案】52 【解析】试题解析：155112121277225⎛⎫⎛⎫⨯--⨯+-÷ ⎪ ⎪⎝⎭⎝⎭ 355515277227⎛⎫=⨯+⨯+-⨯ ⎪⎝⎭53517222⎛⎫=⨯+- ⎪⎝⎭ 5772=⨯ 5.2= 33. 411110.563⎡⎤⎛⎫⨯⨯ ⎪⎢⎥⎝⎭⎣⎦－－－－. 【答案】3【解析】试题解析：411110.563⎡⎤⎛⎫----⨯⨯ ⎪⎢⎥⎝⎭⎣⎦111166⎡⎤⎛⎫=----⨯ ⎪⎢⎥⎝⎭⎣⎦()115=---()14=---14=-+3.=34. 计算：()528522514⎛⎫-+÷-⨯- ⎪⎝⎭ 【答案】32-【解析】【分析】根据有理数混合运算法则可以解答本题．【详解】原式=5281525214-+⨯⨯ =512-+ =32-． 【点睛】本题考查了有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．35. 8+()23-()2⨯-【答案】-10【解析】试题解析：()()()()283289281881810.+-⨯-=+⨯-=+-=-=- 四、化简求值题（每题4分，共8分） 36. m =2，n =3，求m+n 的值【答案】M=2± n=3± m+n=15±±或【解析】试题解析：2, 2.m m =∴=±3, 3.n n =∴=±当2,3m n ==时，23 5.m n +=+=当2,3m n ==-时，23 1.m n +=-=-当2,3m n =-=时，23 1.m n +=-+=当2,3m n =-=-时，()()23 5.m n +=-+-=-综上所述：1m n +=±或 5.±37. 若|x －2|+|y+3|+|z －5|=0计算：(1)x ，y ，z 的值.(2)求|x|+|y|+|z|的值.【答案】X=2 y=-3 z=5 10x y z ++= 【解析】 【分析】 20,30,50.x y z -≥+≥-≥而它们的和为0，则它们都为0，就可以计算出,,x y z 的值.【详解】()1 20,30,50.x y z -≥+≥-≥2350.x y z -+++-=20,30,50.x y z -=+=-=2,3, 5.x y z ==-= ()223523510.x y z ++=+-+=++=【点睛】考核知识点：绝对值非负数性质运用.五、解答题（39题7分，41题6分，43题7分，其他题4分）38. 把下列各数分别填在题后相应的集合中：52-，0，1-，0.73，2，5-，78，29.52-，+28． （1）正数集合：（2）负数集合：（3）整数集合：（4）分数集合：（5）正整数集合：（6）负整数集合：（7）正分数集合：【答案】（1）0.73,2,7/8，+28 （2）-5/2，-1，-5，-29.52（3）0，-1，2，-5，+28 （4）-5/2，0.73,7/8，-29.52,+28 （6）-1，-5(7)0.73,7/8【解析】试题分析：根据正数，负数，整数，分数，正整数，负整数，正分数的概念判断即可.试题解析：()1正数集合：70.73,2,,288+. ()2负数集合：51529.522----，，，. ()3整数集合：012528.，，，，--+()4分数集合：570.73,29.52.28--，， ()5正整数集合：228.+，()6负整数集合：1 5.--，()7正分数集合：70.73,.8点睛：整数包含正整数，0，负整数.注意：0既不是正数也不是负数.39. 某地一天中午12时的气温是6°C，傍晚5时的气温比中午12时下降了4°C，凌晨4时的温度比傍晚5时还低4°C，问傍晚5时的气温是多少？凌晨4时的气温是多少？【答案】2，-2【解析】试题解析：傍晚5时的气温是：642.-=℃凌晨4时的气温是：242.-=-℃答：傍晚5时的气温是2.℃ 凌晨4时的气温是2.-℃40. 某摩托车厂本周计划每日生产450辆摩托车，由于工人实行轮休， 每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表： [增加的辆数为正数，减少的辆数为负数]（1）本周星期六生产多少辆摩托车？（2）本周总产量与计划产量相比，是增加了还是减少了？为什么?（3）产量最多的那天比产量最少的那天多生产多少辆？【答案】（1）441；（2）减少了；（3）35【解析】【分析】（1）用计划生产的辆数加上增减的辆数，计算即可得解；（2）把本周增减的辆数相加，再根据正数和负数的意义解答；（3）用周五增减的辆数减去周日增减的辆数计算即可解答.【详解】解：（1）()4509441+-=（辆）.（2）()()()()()()()57341092521-+++-+++++-+-=-因为-21<0，所以本周总产量与计划产量相比，减少了.（3）由表格可知，周五的产量最多，周日产量最少得：()()102535+--=（辆）答：产量最多的那天比产量最少的那天多生产35辆.【点睛】本题考查了正数和负数，解题的关键是理解正负数的相对性，明确什么是一对具有相反意义的量. 41. 画一条数轴，然后在数轴上画出表示下列各数的点；并求它们的相反数，它们的绝对值，比较它们大小．－12，2，3，－2.7，12005)x y （+，－3，0【答案】（1）3/2, -2 -3 2.7 -4/3 3 0(2)3/2 2 3 2.7 4/3 3 0（3）-3<-2.7<-3/2<0<4/3<2<3【解析】试题分析：画数轴，把这7个数在数轴上表示.就可以看出它们的大小关系. 试题解析：数轴如下：3-的相反数是3,3-的绝对值是3.2.7-的相反数是2.7, 2.7-的绝对值是2.7.112-的相反数是112,112-的绝对值是112. 0的相反数是0,0的绝对值是0.113的相反数是113-,113的绝对值是113. 2的相反数是2-,2的绝对值是2.3的相反数是3-,3的绝对值是3. 它们的大小顺序是：113 2.71012 3.23-<-<-<<<< 点睛：数轴上，右边的数总比左边的数大.42. 观察下列各式：1223121122112221=+=++=－，－，－，……猜想：（1）236312222++++⋯+=_________；（2）如果n 为正整数，那么2312222n ++++⋯+=_________.【答案】 (1). 6421- (2). 121n +-【解析】【分析】【详解】试题分析：观察所给式子，找规律.试题解析：()2363641122222 1.++++⋯+=- ()2312122222 1.n n +++++⋯+=-故答案为()6412 1.-()122 1.n +-。

北京市昌平临川育人学校2017-2018学年七年级数学下学期期中试题（B 卷）一、选择题（每小题2分，共计20分） 1.下列计算正确的是（ ）A. 248a a a =÷B. 532x x x =+C.853)()(c c c =-∙- D.22))((y x y x y x +-=+---2. H7N9禽流感病毒的直径大约是0.000000081米，用科学记数法可表示为（ ）A. 8.1×10-9米 B. 8.1×10-8米 C. 81×10-9米 D. 0.81×10-7米 3. 单项式A 与-3x 2y 的乘积是6x 6y 2，则单项式A 是（ ）A. 2x 3y B. -2x 3y C. -2x 4y D. 2x 4y 4．尺规作图所用的作图工具是指( )． A ．刻度尺和圆规 B ．不带刻度的直尺和圆规 C ．刻度尺D ．圆规5．下列语句不正确的是 A ．对顶角相等 B ．两点之间线段最短 C ．同旁内角互补D ．延长线段AB 到C6. 如图,1∠与2∠是对顶角的是7．计算：3－2的结果是( )． A ．－9 B ．－6 C ．－19 D.198. 已知：如图AB ∥CD ，CE 平分∠ACD ，∠A=110°，则∠ECD 等于A.110°B.70°C.55°D.35°9.骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，因变量是（ ）A 、沙漠B 、体温C 、时间D 、骆驼10．如图，E 为BC 上一点，AB ∥C D∥EF ，AE ∥CG ，则图中与∠A （不包括∠A ）相等的角有CA BED第8题图A ．5个B ．4个C ．3个D ．2个二、填空题（每小题2分，共20分）11.如图，写一个使AB ∥CD 的条件 。

12. 若a m=2，a n=4，则a m-n=________.13. 计算：（9a 2b-6ab 2）÷（3ab ）= .14.在“变量之间的关系”一章中，我们学习的“变量”是指自变量和因变量，而表达它们之间的关系通常有三种方法，这三种方法是指 、 和 ．15．两条直线相交所成的四个角中，有一组邻补角相等时，这两条直线的位置关系是____． 16．PM 2.5即细颗粒物，指环境空气中直径小于等于 0.0000025 米的颗粒物，这个数据用科学记数法表示为___________________.17．如图，用量角器量一个破损的扇形零件的圆心角，请写出这个圆心角的度数是______，根据是_______________________________.18．16.若622=-n m ，且3=-n m ，则=+n m ． 19、平行线的性质： 平行线的判定：（1）两直线平行， ；（4） ，两直线平行； （2）两直线平行， ；（5） ，两直线平行； （3）两直线平行， ；（6） ，两直线平行。

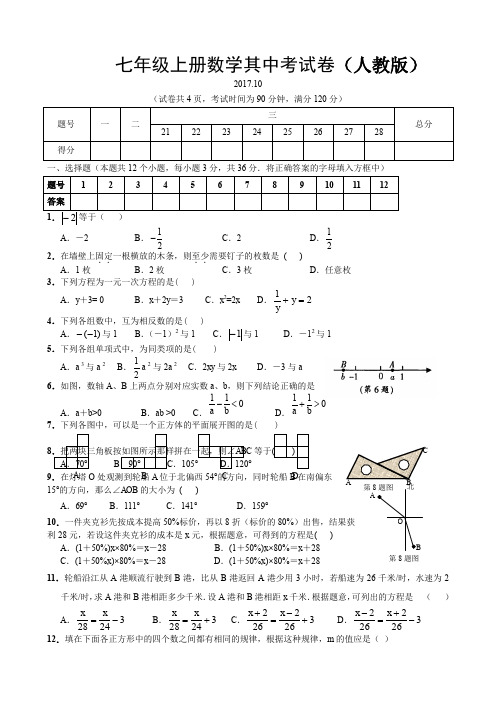
七年级上册数学其中考试卷（人教版）2017.10（试卷共4页，考试时间为90分钟，满分120分）一、选择题（本题共12个小题，每小题3分，共36分．将正确答案的字母填入方框中） A ．－2 B ．12-C ．2D ．122．在墙壁上固定．．一根横放的木条，则至少．．需要钉子的枚数是 ( ) A ．1枚 B ．2枚 C ．3枚 D ．任意枚3．下列方程为一元一次方程的是( ) A ．y ＋3= 0B ．x ＋2y ＝3C ．x 2=2xD ．21=+y y4．下列各组数中，互为相反数的是( )A ．)1(--与1B ．（－1）2与1C ．1-与1D ．－12与15．下列各组单项式中，为同类项的是( ) A ．a 3与a 2B ．12a 2与2a 2C ．2xy 与2xD ．－3与a 6．如图，数轴A 、B 上两点分别对应实数a 、b ，则下列结论正确的是A ．a ＋b>0B ．ab >0C ．110a b -<D ．110a b +>7．下列各图中，可以是一个正方体的平面展开图的是( )8．把两块三角板按如图所示那样拼在一起，则∠ABC 等于( ) A．70° B ．90° C ．105°D ．120°9．在灯塔O 处观测到轮船A 位于北偏西54°的方向，同时轮船B 在南偏东15°的方向，那么∠AOB 的大小为 ( ) A ．69° B ．111° C ．141° D ．159°10．一件夹克衫先按成本提高50%标价，再以8折（标价的80%）出售，结果获 利28元，若设这件夹克衫的成本是x 元，根据题意，可得到的方程是( ) A ．(1＋50%)x×80%＝x －28 B ．(1＋50%)x×80%＝x ＋28 C ．(1＋50%x)×80%＝x －28 D ．(1＋50%x)×80%＝x ＋2811．轮船沿江从A 港顺流行驶到B 港，比从B 港返回A 港少用3小时，若船速为26千米/时，水速为2千米/时，求A 港和B 港相距多少千米．设A 港和B 港相距x 千米．根据题意，可列出的方程是 （ ） A ．32428-=x x B ．32428+=x x C ．3262262+-=+x x D ．3262262-+=-x x 12．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m 的值应是（ ）A B C D 第第8题图A ．110B ．158C ．168二、填空题（本大题共8个小题；每小题3分，共24 13．－3的倒数是________．14．单项式12-xy 2的系数是_________．15．若x =2是方程8－2x =ax 的解，则a =_________． 16．计算：15°37′+42°51′=_________．17．青藏高原是世界上海拔最高的高原，它的面积约为2 500 000平方千米．将2 500 000用科学记数法表示应为_________________平方千米． 18．已知，a －b =2，那么2a －2b +5=_________．19．已知y 1=x ＋3，y 2=2－x ，当x =_________时，y 1比y 2大5． 20．根据图中提供的信息，可知一个杯子的价格是________元．三、解答题（本大题共8个小题；共60分）21．（本小题满分6分）计算：(－1)3－14×[2－(－3)2] ． 22．（本小题满分6分）一个角的余角比这个角的21少30°，请你计算出这个角的大小．23．（本小题满分7分） 先化简，再求值：41（－4x 2+2x －8）－（21x －1），其中x =21． 24．（本小题满分7分） 解方程：513x +－216x -=1．25．（本小题满分7分）一点A 从数轴上表示+2的点开始移动，第一次先向左移动1个单位，再向右移动2个单位；第二次先向左移动3个单位，再向右移动4个单位；第三次先向左移动5个单位，再向右移动6个单位…… （1）写出第一次移动后这个点在数轴上表示的数为 ； （2）写出第二次移动结果这个点在数轴上表示的数为 ； （3）写出第五次移动后这个点在数轴上表示的数为 ； （4）写出第n 次移动结果这个点在数轴上表示的数为 ； （5）如果第m 次移动后这个点在数轴上表示的数为56，求m 的值． 26．（本小题满分8分）如图，∠AOB =∠COD =90°，OC 平分∠AOB ，∠BOD =3∠DOE ． 求：∠COE 的度数． 27．（本小题满分8分）6 2 224 2 0 4 88 4 446 (43)共94元如图，已知线段AB 和CD 的公共部分BD =13AB =14CD ，线段AB 、CD 的中点E 、F 之间距离是10cm ，求AB 、CD 的长．28．（本小题满分11分）某中学为了表彰在书法比赛中成绩突出的学生，购买了钢笔30支，毛笔45支，共用了1755元，其中每支毛笔比钢笔贵4元．（1）求钢笔和毛笔的单价各为多少元？（2）①学校仍需要购买上面的两种笔共105支（每种笔的单价不变）．陈老师做完预算后，向财务处王老师说：“我这次买这两种笔需支领2447元．”王老师算了一下，说：“如果你用这些钱只买这两种笔，那么帐肯定算错了．”请你用学过的方程知识．．．．解释王老师为什么说他用这些钱只买这两种笔的帐算错了． ②陈老师突然想起，所做的预算中还包括校长让他买的一支签字笔．如果签字笔的单价为小于10元的整数，请通过计算，直接．．写出签字笔的单价可能为 元． 2012～2013学年度第一学期七年级期末考试数学试题参考答案及评分说明说明： 1.各校在阅卷过程中，如还有其它正确解法，可参照评分标准按步骤酌情给分． 2．坚持每题评阅到底的原则，当学生的解答在某一步出现错误，影响了后继部分时，如果该步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严重的错误，就不给分． 一、选择题（每小题3分，共36分）1．C ；2．B ；3．A ；4．D ；5．B ；6. D ；7．C ；8．D ；9．C ；10. B ；11．A ；12．B . 二、填空题（每题3分，共24分） 13．31-；14．21-；15．2；16．58°28′；17．2.5×106；18．9；19．2；20．8. 三、解答题（共60分）21．解：原式= －1－14×（2－9） ………………………………………………………3分 =－1+ 47…………………………………………………………………………5分=43……………………………………………………………………………6分22．解：设这个角的度数为x . ……………………………………………………………1分由题意得：30)90(21=--x x ………………………………………………3分 解得：x =80 …………………………………………………………………5分 答：这个角的度数是80° ……………………………………………………………6分 23．解：原式 =1212212+--+-x x x ………………………………………………3分 =12--x ………………………………………………………………4分AE DBFC把x =21代入原式： 原式=12--x =1)21(2--……………………………………………………………5分=45- ……………………………………………………………………………7分24．解：6)12()15(2=--+x x . ……………………………………………2分612210=+-+x x . ………………………………………………………4分8x =3. …………………………………………………………6分83=x . …………………………………………………………7分 25．解：（1）第一次移动后这个点在数轴上表示的数是3； ……………………………1分（2）第二次移动后这个点在数轴上表示的数是4； ……………………………2分 （3）第五次移动后这个点在数轴上表示的数是7； ……………………………3分 （4）第n 次移动后这个点在数轴上表示的数是n +2； …………………………5分 （5）54. ………………………………………………………………………7分 26．解：∵∠AOB =90°，OC 平分∠AOB ∴∠BOC =12∠AOB =45°， ………………………………………………………2分 ∵∠BOD =∠COD －∠BOC =90°－45°=45°， ………………………………4分∠BOD =3∠DOE∴∠DOE =15， ……………………………………………………………………7分 ∴∠COE =∠COD －∠DOE =90°－15°=75° …………………………………8分 27．解：设BD =x cm ，则AB =3x cm ，CD =4x cm ，AC =6x cm ． …………………………1分∵点E 、点F 分别为AB 、CD 的中点，∴AE =12AB =1.5x cm ，CF =12CD =2x cm ． ……………………………………………3分 ∴EF =AC －AE －CF =2.5x cm ． ………………………………………………………4分∵EF =10cm ，∴2.5x =10，解得：x =4． ………………………………………………………………6分∴AB =12cm ，CD =16cm ． ……………………………………………………………8分 28．解：（1）设钢笔的单价为x 元，则毛笔的单价为（x +4）元. ………………………1分由题意得：30x +45（x +4）=1755 ……………………………………………3分解得：x =21则x +4=25. ……………………………………………………………………4分 答：钢笔的单价为21元，毛笔的单价为25元. ……………………………………5分 （2）设单价为21元的钢笔为y 支，所以单价为25元的毛笔则为(105－y )支. …6分 根据题意，得21y +25(105－y )=2447.………………………………………………7分 解之得：y =44.5 (不符合题意) . ……………………………………………………8分 所以王老师肯定搞错了. ……………………………………………………………9分 （3）2或6. ………………………………………………………………………11分〖答对1个给1分，答错1个倒扣1分，扣到0分为止〗28．（3）解法提示：设单价为21元的钢笔为z 支，签字笔的单价为a 元 则根据题意，得21z+25(105－z)=2447－a.即：4z=178+a，因为a、z都是整数，且178+a应被4整除，所以a为偶数，又因为a为小于10元的整数，所以a可能为2、4、6、8. 当a=2时，4z=180，z=45，符合题意；当a=4时，4z=182，z=45.5，不符合题意；当a=6时，4z=184，z=46，符合题意；当a=8时，4z=186，z=46.5，不符合题意.所以笔记本的单价可能2元或6元.〖本题也可由①问结果，通过讨论钢笔单价得到答案〗。

七年级（上）期中数学试卷一、选择题（本大题共10小题，共30.0分）1.-2的相反数是（）A. B. C. D. 22.在-，0，，-1这四个数中，最小的数是（）A. B. 0 C. D.3.有理数a，b在数轴上的对应点如图所示，则下面式子中正确的是（）A. B. C. D.4.A、B两地相距6980000m，用科学记数法表示为（）m．A. B. C. D.5.下面各式中，与-2xy2是同类项的是（）A. B. C. D.6.一个长方形的一边长是2a+3b，另一边的长是a+b，则这个长方形的周长是（）A. B. C. D.7.下列代数式书写规范的是（）A. B. C. ax3 D.8.关于多项式x5-3x2-7，下列说法正确的是（）A. 最高次项是5B. 二次项系数是3C. 常数项是7D. 是五次三项式9.在代数式：，3m-3，-22，-，2πb2中，单项式的个数有（）A. 1个B. 2个C. 3个D. 4个10.如果x是最大的负整数，y绝对值最小的整数，则-x2016+y的值是（）A. B. C. 1 D. 2016二、填空题（本大题共10小题，共20.0分）11.的绝对值是______ ，的倒数是______ ．12.在数轴上，若点P表示-2，则距P点3个单位长的点表示的数是______ ．13.单项式-5πab2的系数是______ ，次数是______ ．14.如图是一数值转换机，若输入的x为-1，则输出的结果为______ ．15.绝对值小于3的所有整数的和是______ ．16.数轴上表示数-5和表示-14的两点之间的距离是______ ．17.在数4.3，-，|0|，-（-），-|-3|，-（+5）中，______ 是正数．18.已知|a|=2，|b|=5，且ab＜0，那么a+b的值为______ ．19.如果有|x-3|+（y+4）2=0，则x= ______ ，y x= ______ ．20.现规定一种新的运算“*”：a*b=a b，如3*2=32=9，则（）*3= ______ ．三、解答题（本大题共13小题，共66.0分）21.把下面的有理数填在相应的大括号里：（★友情提示：将各数用逗号分开）15，，0，-30，0.15，-128，，+20，-2.6正数集合﹛______﹜负数集合﹛______﹜整数集合﹛______﹜分数集合﹛______﹜22.计算：28-37-3+52．23.计算：（-+）÷（-）24.计算（-4）×（-9）+（-）-23．25.化简：3x2-3+x-2x2+5．26.化简（5a-3a2+1）-（4a3-3a2）．27.观察图形，写出一个与阴影面积有关的代数恒等式．28.（1）在数轴上表示下列各数，（2）用“＜”连接：-3.5，，-1，4，0，2.5．29.先化简，再求值：5（a2b-ab2）-（ab2+5a2b），其中a=1，b=-2．30.10盒火柴如果以每盒100根为准，超过的根数记作正数，不足的根数记作负数，每盒数据记录如下：+3，+2，0，-1，-2，-3，-2，+3，-2，-2．求：这10盒火柴共有多少根．31.已知有理数a，b，c在数轴上的位置如图所示，（1）用＜，＞，=填空：a+c ______ 0，c-b ______ 0，b+a ______ 0，abc ______ 0；（2）化简：|a+c|+|c-b|-|b+a|．32.阅读下列解题过程，然后答题：已知如果两个数互为相反数，则这两个数的和为0，例如，若x和y互为相反数，则必有x+y=0．（1）已知：|a|+a=0，求a的取值范围．（2）已知：|a-1|+（a-1）=0，求a的取值范围．33.我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b3展开式中的系数等等．（1）根据上面的规律，写出（a+b）5的展开式．（2）利用上面的规律计算：25-5×24+10×23-10×22+5×2-1．答案和解析1.【答案】D【解析】解：-2的相反数是2，故选：D．根据相反数的定义：只有符号不同的两个数叫做互为相反数即可得到答案．此题主要考查了相反数，关键是掌握相反数的定义．2.【答案】D【解析】解：根据有理数大小比较的法则，可得-1＜-，所以在-，0，，-1这四个数中，最小的数是-1．故选：D．有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．3.【答案】D【解析】解：∵从数轴可知：b＜0＜a，|b|＞|a|，∴A错误；B错误；∵a＞0，b＜0，∴ab＜0，∴C错误；∵b＜0＜a，|b|＞|a|，∴a-b＞0，a+b＜0，∴a-b＞a+b，∴D正确；故选D．数轴可知b＜0＜a，|b|＞|a|，求出ab＜0，a-b＞0，a+b＜0，根据以上结论判断即可．本题考查了数轴，有理数的乘法、加法、减法等知识点的应用，关键是能根据数轴得出b＜0＜a，|b|＞|a|．4.【答案】D【解析】解：6980000=6.98×106，故选：D．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．5.【答案】A【解析】解：由题意，得y2x与-2xy2是同类项，故选：A．根据同类项的定义，所含字母相同且相同字母的指数也相同的项是同类项，可得答案．本题考查同类项的定义，同类项定义中的两个“相同”：所含字母相同；相同字母的指数相同，是易混点，还有注意同类项定义中隐含的两个“无关”：①与字母的顺序无关；②与系数无关．6.【答案】B【解析】解：周长=2(2a+3b+a+b）=6a+8b．故选B．长方形的周长等于四边之和，由此可得出答案．本题考查有理数的加减运算，比较简单，注意长方形的周长可表示为2（长加宽）．7.【答案】A【解析】解：选项A正确，B正确的书写格式是b，C正确的书写格式是3ax，D正确的书写格式是．故选A．根据代数式的书写要求判断各项即可得出正确答案．代数式的书写要求：（1）在代数式中出现的乘号，通常简写成“•”或者省略不写；（2）数字与字母相乘时，数字要写在字母的前面；（3）在代数式中出现的除法运算，一般按照分数的写法来写．带分数要写成假分数的形式．8.【答案】D【解析】解：A、多项式x5-3x2-7的最高次项是x5，故本选项错误；B、多项式x5-3x2-7的二次项系数是-3，故本选项错误；C、多项式x5-3x2-7的常数项是-7，故本选项错误；D、多项式x5-3x2-7是五次三项式，故本选项正确．故选：D．根据多项式的项和次数的定义，确定各个项和各个项的系数，注意要带有符号．本题考查与多项式相关的概念，多项式中每个单项式叫做多项式的项，这些单项式中的最高次数，就是这个多项式的次数．9.【答案】C【解析】解：-22，-，2πb2中是单项式；是分式；3m-3是多项式．故选C．根据单项式的定义进行解答即可．本题考查的是单项式，熟知数或字母的积组成的式子叫做单项式，单独的一个数或字母也是单项式是解答此题的关键．10.【答案】B【解析】解：∵x是最大的负整数，y绝对值最小的整数，∴x=-1，y=0，∴-x2016+y=-（-1）2016=-1．故选B．由于x是最大的负整数，y绝对值最小的整数，由此可以分别确定x=-1，y=0，把它们代入所求代数式计算即可求解．此题主要考查了有理数的混合运算，解题的关键是根据最大的负整数，绝对值最小的整数的性质确定x、y的值，然后代入所求代数式即可解决问题．11.【答案】；【解析】解：-的绝对值为，1的倒数为．故答案为：，．根据绝对值、倒数，即可解答．本题考查了绝对值、倒数，解决本题的关键是熟记绝对值、倒数的定义．12.【答案】-5或1【解析】解：设距P点3个单位长的点表示的数是x，则|x+2|=3，当x+2≥0时，原式可化为：x+2=3，解得x=1；当x+2＜0时，原式可化为：-x-2=3，解得x=-5．故答案为：-5或1．设距P点3个单位长的点表示的数是x，则|x+2|=3，求出x的值即可．本题考查的是数轴，熟知数轴上两点间的距离公式是解答此题的关键．13.【答案】-5π；3【解析】解：单项式-5πab2的系数是-5π，次数是3．故答案为：-5π，3．根据单项式系数、次数的定义来求解．单项式中数字因数叫做单项式的系数，所有字母的指数和叫做这个单项式的次数．此题考查了单项式，确定单项式的系数和次数时，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数和次数的关键．14.【答案】9【解析】解：（-1-2）×（-3）=（-3）×（-3）=9．故答案为：9．根据运算规则：先-2，再×（-3），进行计算即可求解．此题主要考察根据运算规则列式计算，读懂题中的运算规则，并准确代入求值是解题的关键．15.【答案】0【解析】解：根据绝对值的意义得绝对值小于3的所有整数为0，±1，±2．所以0+1-1+2-2=0．故答案为：0．绝对值的意义：一个数的绝对值表示数轴上对应的点到原点的距离．互为相反数的两个数的和为0．依此即可求解．此题考查了绝对值的意义，并能熟练运用到实际当中．16.【答案】9【解析】解：|-5-（-14）|=9．数轴上两点之间的距离等于这两点的数的差的绝对值，即较大的数减去较小的数．考查了数轴上两点之间的距离的计算方法．17.【答案】4.3，-（-）【解析】解：在数4.3，-，|0|，-（-）=，-|-3|=-3，-（+5）=-5中，4.3，-（-）是正数．故答案为：4.3，-（-）．首先将各数化简，再根据正数的定义可得结果．本题主要考查了有理数的定义，熟练掌握有理数的分类是解答此题的关键．18.【答案】3或-3【解析】解：①a＞0，b＜0，则a=2，b=-5，a+b=-3；②a＜0，b＞0，则a=-2，b=5，a+b=3．故填3或-3．根据题意可得a和b异号，分情况讨论①a＞0，b＜0；②a＜0，b＞0．本题考查有理数的加法，注意讨论a和b的取值范围得出a和b的值是关键．19.【答案】3；-64【解析】解：由题意得，x-3=0，y+4=0，解得，x=3，y=-4，则y x=-64，故答案为：3；-64．根据非负数的性质列出方程求出x、y的值，代入所求代数式计算即可．本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．20.【答案】【解析】解：∵a*b=a b，3*2=32=9，∴（）*3=（-）3=-．故答案为：-．根据题中所给出的运算方法列出乘方的式子，再根据乘方的运算法则进行计算即可．本题考查的是有理数的混合运算，熟知数的乘方法则是解答此题的关键．21.【答案】15，0.15，，+20；，-30，-128，-2.6；15，0，-30，-128，+20；，0.15，，-2.6【解析】解：正数集合﹛15，0.15，，+20，﹜负数集合﹛，-30，-128，-2.6，﹜整数集合﹛15，0，-30，-128，+20，﹜分数集合﹛，0.15，，-2.6，﹜按照有理数的分类填写：有理数．认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点．注意整数和正数的区别，注意0是整数，但不是正数．22.【答案】解：28-37-3+52，=28+52-37-3，=80-40，=40．【解析】先根据加法交换律将同号数相加，再把两个异号数相加．本题是有理数的加减混合运算，可以看作是省略加号的加法，注意运用简便算法进行计算．23.【答案】解：原式=（-+）×（-36），=×（-36）-×（-36）+×（-36），=-8+9-2，=-1．【解析】首先根据除以一个不为0的数等于乘以这个数的倒数可得（-+）×（-36），再用乘法分配律计算即可．此题主要考查了有理数的除法，关键是掌握有理数除法法则：除以一个不等于0的数，等于乘这个数的倒数．24.【答案】解：（-4）×（-9）+（-）-23=36+（-）-8=27．【解析】根据有理数的乘法和加减法可以解答本题．本题考查有理数的混合运算，解题的关键是明确有理数混合运算的计算方法．25.【答案】解：3x2-3+x-2x2+5=（3x2-2x2）+x+（5-3）=x2+x+2．【解析】首先找出同类项，进而合并同类项得出答案．此题主要考查了合并同类项，正确找出同类项是解题关键．26.【答案】解：（5a-3a2+1）-（4a3-3a2）=5a-3a2+1-4a3+3a2=-4a3+5a+1．【解析】先去括号，然后合并同类项即可解答本题．本题考查整式的加减，解题的关键是明确整式的加减的计算方法，注意去括号后，各项内的符号是否变号．27.【答案】解：阴影部分的面积可表示为：a2-b2或（a+b）（a-b），∴a2-b2=（a+b）（a-b）．【解析】分别利用不同的方法表示出阴影部分的面积，得到恒等式．本题考查的是平方差公式的几何背景，掌握平方差公式、矩形的面积公式是解题的关键．28.【答案】解：（1）如图所示：（2）-3.5＜-1＜0＜＜2.5＜4【解析】在数轴上表示各数，数轴上各数从左往右的顺序，就是各数从小到大的顺序．本题考查了用数轴表示有理数和有理数的大小比较．数轴上各数从左往右的顺序就是各数从小到大的顺序．29.【答案】解：原式=5a2b-5ab2-ab2-5a2b=-6ab2，∴当a=1，b=-2时，∴原式=-6×1×4=-24【解析】先将原式化简，然后将a与b的值代入即可求出答案．本题考查整式运算，涉及代入求值．30.【答案】解：先求超过的根数：（+3）+（+2）+0+（-1）+（-2）+（-3）+（-2）+（+3）+（-2）+（-2）=-4；则10盒火柴的总数量为：100×10-4=996（根）．答：10盒火柴共有996根．【解析】首先审清题意，明确“正”和“负”所表示的意义；然后根据每盒的数据记录求出超过的根数，进而可求得10盒火柴的总数量．解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．31.【答案】＜；＞；＜；＞【解析】解：（1）根据数轴可知：a＜b＜0＜c，且|c|＜|b|＜|a|，∴a+c＜0，c-b＞0，b+a＜0，abc＞0，故答案为：＜，＞，＜，＞；（2）原式=-（a+c）+（c-b）+（b+a）=-a-c+c-b+b+a=0．（1）根据数轴，判断出a，b，c的取值范围，进而求解；（2）根据绝对值的性质，去绝对值号，合并同类项即可．本题主要考查数轴、绝对值、整式的加减等知识的综合运用，解决此题的关键是能够根据数轴上的信息，判断出a，b，c等字母的取值范围，同时解决此题时也要注意绝对值性质的运用．32.【答案】解：（1）∵|a|≥0，|a|+a=0，∴a≤0；（2）∵|a-1|≥0，∴a-1≤0，解得a≤1．【解析】（1）根据绝对值的性质可得出|a|≥0，再由相反数的定义即可得出结论；（2）根据绝对值的性质可得出|a-1|≥0，再由相反数的定义即可得出结论．本题考查的是有理数的加法，熟知相反数的定义是解答此题的关键．33.【答案】解：（1）如图，则（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5；（2）25-5×24+10×23-10×22+5×2-1．=25+5×24×（-1）+10×23×（-1）2+10×22×（-1）3+5×2×（-1）4+（-1）5．=（2-1）5，=1．【解析】（1）直接根据图示规律写出图中的数字，再写出（a+b）5的展开式；（2）发现这一组式子中是2与-1的和的5次幂，由（1）中的结论得：25-5×24+10×23-10×22+5×2-1=（2-1）5，计算出结果．本题考查了完全式的n次方，也是数字类的规律题，首先根据图形中数字找出对应的规律，再表示展开式：对应（a+b）n中，相同字母a的指数是从高到低，相同字母b的指数是从低到高．。

七年级上册数学其中考试卷（人教版）（试卷共4页，考试时间为90分钟，满分120分）题号 一二三总分2122232425262728得分一、选择题（本题共12个小题，每小题3分，共36分．将正确答案的字母填入方框中） 题号 123456789101112答案1．2-等于（ ）A ．－2B ．12-C ．2D ．122．在墙壁上固定．．一根横放的木条，则至少．．需要钉子的枚数是 ( ) A ．1枚 B ．2枚 C ．3枚 D ．任意枚3．下列方程为一元一次方程的是( ) A ．y ＋3= 0B ．x ＋2y ＝3C ．x 2=2xD ．21=+y y4．下列各组数中，互为相反数的是( )A ．)1(--与1B ．（－1）2与1C ．1-与1D ．－12与15．下列各组单项式中，为同类项的是( ) A ．a 3与a 2B ．12a 2与2a 2C ．2xy 与2xD ．－3与a 6．如图，数轴A 、B 上两点分别对应实数a 、b ，则下列结论正确的是A ．a ＋b>0B ．ab >0C ．110a b -<D ．110a b +>7．下列各图中，可以是一个正方体的平面展开图的是( )8．把两块三角板按如图所示那样拼在一起，则∠ABC 等于( ) A ．70° B ．90° C ．105° D ．120°9．在灯塔O 处观测到轮船A 位于北偏西54°的方向，同时轮船B 在南偏东15°的方向，那么∠AOB 的大小为 ( ) A ．69° B ．111° C ．141° D ．159°10．一件夹克衫先按成本提高50%标价，再以8折（标价的80%）出售，结果获 利28元，若设这件夹克衫的成本是x 元，根据题意，可得到的方程是( ) A ．(1＋50%)x×80%＝x －28 B ．(1＋50%)x×80%＝x ＋28 C ．(1＋50%x)×80%＝x －28 D ．(1＋50%x)×80%＝x ＋2811．轮船沿江从A 港顺流行驶到B 港，比从B 港返回A 港少用3小时，若船速为26千米/时，水速为2千米/时，求A 港和B 港相距多少千米．设A 港和B 港相距x 千米．根据题意，可列出的方程是 （ ） A ．32428-=x x B ．32428+=x x C ．3262262+-=+x x D ．3262262-+=-x x 12．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m 的值应是（ ）A B C D 6 2 224 20 4 884 446 m10 ……AB C第8题图 北O AB第8题图A ．110B ．158C ．168D ．178二、填空题（本大题共8个小题；每小题3分，共24分．把答案写在题中横线上） 13．－3的倒数是________．14．单项式12-xy 2的系数是_________．15．若x =2是方程8－2x =ax 的解，则a =_________． 16．计算：15°37′+42°51′=_________．17．青藏高原是世界上海拔最高的高原，它的面积约为2 500 000平方千米．将2 500 000用科学记数法表示应为_________________平方千米． 18．已知，a －b =2，那么2a －2b +5=_________．19．已知y 1=x ＋3，y 2=2－x ，当x =_________时，y 1比y 2大5． 20．根据图中提供的信息，可知一个杯子的价格是________元．三、解答题（本大题共8个小题；共60分）21．（本小题满分6分）计算：(－1)3－14×[2－(－3)2] ． 22．（本小题满分6分）一个角的余角比这个角的21少30°，请你计算出这个角的大小．23．（本小题满分7分） 先化简，再求值：41（－4x 2+2x －8）－（21x －1），其中x =21． 24．（本小题满分7分） 解方程：513x +－216x -=1．25．（本小题满分7分）一点A 从数轴上表示+2的点开始移动，第一次先向左移动1个单位，再向右移动2个单位；第二次先向左移动3个单位，再向右移动4个单位；第三次先向左移动5个单位，再向右移动6个单位…… （1）写出第一次移动后这个点在数轴上表示的数为 ； （2）写出第二次移动结果这个点在数轴上表示的数为 ； （3）写出第五次移动后这个点在数轴上表示的数为 ； （4）写出第n 次移动结果这个点在数轴上表示的数为 ； （5）如果第m 次移动后这个点在数轴上表示的数为56，求m 的值． 26．（本小题满分8分）如图，∠AOB =∠COD =90°，OC 平分∠AOB ，∠BOD =3∠DOE ． 求：∠COE 的度数． 27．（本小题满分8分）共43元共94元 CB E D如图，已知线段AB 和CD 的公共部分BD =13AB =14CD ，线段AB 、CD 的中点E 、F 之间距离是10cm ，求AB 、CD 的长．28．（本小题满分11分）某中学为了表彰在书法比赛中成绩突出的学生，购买了钢笔30支，毛笔45支，共用了1755元，其中每支毛笔比钢笔贵4元．（1）求钢笔和毛笔的单价各为多少元（2）①学校仍需要购买上面的两种笔共105支（每种笔的单价不变）．陈老师做完预算后，向财务处王老师说：“我这次买这两种笔需支领2447元．”王老师算了一下，说：“如果你用这些钱只买这两种笔，那么帐肯定算错了．”请你用学过的方程知识．．．．解释王老师为什么说他用这些钱只买这两种笔的帐算错了． ②陈老师突然想起，所做的预算中还包括校长让他买的一支签字笔．如果签字笔的单价为小于10元的整数，请通过计算，直接．．写出签字笔的单价可能为 元． 2012～2013学年度第一学期七年级期末考试数学试题参考答案及评分说明说明： 1.各校在阅卷过程中，如还有其它正确解法，可参照评分标准按步骤酌情给分． 2．坚持每题评阅到底的原则，当学生的解答在某一步出现错误，影响了后继部分时，如果该步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严重的错误，就不给分． 一、选择题（每小题3分，共36分）1．C ；2．B ；3．A ；4．D ；5．B ；6. D ；7．C ；8．D ；9．C ；10. B ；11．A ；12．B . 二、填空题（每题3分，共24分） 13．31-；14．21-；15．2；16．58°28′；17．×106；18．9；19．2；20．8. 三、解答题（共60分）21．解：原式= －1－14×（2－9） ………………………………………………………3分 =－1+ 47…………………………………………………………………………5分=43……………………………………………………………………………6分22．解：设这个角的度数为x . ……………………………………………………………1分由题意得：30)90(21=--x x ο ………………………………………………3分 解得：x =80 …………………………………………………………………5分 答：这个角的度数是80° ……………………………………………………………6分 23．解：原式 =1212212+--+-x x x ………………………………………………3分 =12--x ………………………………………………………………4分AE DBFC把x =21代入原式： 原式=12--x =1)21(2--……………………………………………………………5分=45- ……………………………………………………………………………7分24．解：6)12()15(2=--+x x . ……………………………………………2分612210=+-+x x . ………………………………………………………4分8x =3. …………………………………………………………6分83=x . …………………………………………………………7分 25．解：（1）第一次移动后这个点在数轴上表示的数是3； ……………………………1分（2）第二次移动后这个点在数轴上表示的数是4； ……………………………2分 （3）第五次移动后这个点在数轴上表示的数是7； ……………………………3分 （4）第n 次移动后这个点在数轴上表示的数是n +2； …………………………5分 （5）54. ………………………………………………………………………7分 26．解：∵∠AOB =90°，OC 平分∠AOB ∴∠BOC =12∠AOB =45°， ………………………………………………………2分 ∵∠BOD =∠COD －∠BOC =90°－45°=45°， ………………………………4分 ∠BOD =3∠DOE∴∠DOE =15， ……………………………………………………………………7分 ∴∠COE =∠COD －∠DOE =90°－15°=75° …………………………………8分 27．解：设BD =x cm ，则AB =3x cm ，CD =4x cm ，AC =6x cm ． …………………………1分∵点E 、点F 分别为AB 、CD 的中点，∴AE =12AB =，CF =12CD =2x cm ． ……………………………………………3分 ∴EF =AC －AE －CF =． ………………………………………………………4分∵EF =10cm ，∴=10，解得：x =4． ………………………………………………………………6分∴AB =12cm ，CD =16cm ． ……………………………………………………………8分 28．解：（1）设钢笔的单价为x 元，则毛笔的单价为（x +4）元. ………………………1分由题意得：30x +45（x +4）=1755 ……………………………………………3分解得：x =21则x +4=25. ……………………………………………………………………4分 答：钢笔的单价为21元，毛笔的单价为25元. ……………………………………5分 （2）设单价为21元的钢笔为y 支，所以单价为25元的毛笔则为(105－y )支. …6分 根据题意，得21y +25(105－y )=2447.………………………………………………7分 解之得：y = (不符合题意) . ……………………………………………………8分所以王老师肯定搞错了. ……………………………………………………………9分 （3）2或6. ………………………………………………………………………11分〖答对1个给1分，答错1个倒扣1分，扣到0分为止〗28．（3）解法提示：设单价为21元的钢笔为z 支，签字笔的单价为a 元 则根据题意，得21z+25(105－z)=2447－a.即：4z=178+a，因为a、z都是整数，且178+a应被4整除，所以a为偶数，又因为a为小于10元的整数，所以a可能为2、4、6、8. 当a=2时，4z=180，z=45，符合题意；当a=4时，4z=182，z=，不符合题意；当a=6时，4z=184，z=46，符合题意；当a=8时，4z=186，z=，不符合题意.所以笔记本的单价可能2元或6元.〖本题也可由①问结果，通过讨论钢笔单价得到答案〗。