6 三角形的尺规作图

《三角形的尺规作图》教案教学目标1、在分别给出的两角夹边、两边夹角和三边的条件下，能够利用尺规作三角形．2、能结合三角形全等的条件与同伴交流作图过程和结果的合理性．教学重点根据题目的条件作三角形．教学难点探索作图过程．教学工具圆规、直尺准备活动(1)计算已知线段a，求作线段AB，使得AB＝a．(2)已知：∠α，求作：∠AOB，使∠AOB＝∠α．(3)已知：M为∠AOB边上的一点，如图所示，过M作直线CD，使得CD//OA．教学过程内容一：(根据简单图形书写作法)(1)如图，使用直尺作图，看图填空．①②③④①过点____和_______作直线AB；②连结线段___________；③以点_______为端点，过点_______作射线___________；④延长线段__________到_________，使得BC＝2AB．(2)如图，使用圆规作图，看图填空：①在射线AM上__________线段________＝___________．②以点______为圆心，以线段______为半径作弧交_________于点___________．③以点______为圆心，以任意长为半径作弧，分别交∠AOB两边，交_________于点__ _________，交________于点__________．这部分内容是为让学生熟悉作法的语言表达而设的．教师应该让学生慢慢理解这种语言表达的意思．逐步学会自己口述表达自己的作图过程．内容二：(作一个三角形与已知三角形全等)1、已知三角形的两边及其夹角，求作这个三角形．已知：线段a，c，∠α．求作：ΔABC，使得BC＝a，AB＝c，∠ABC＝∠α．作法与过程：(1)作一条线段BC＝a，(2)以B为顶点，BC为一边，作角∠DBC＝∠a；(3)在射线BD上截取线段BA＝c；(4)连接AC，ΔABC就是所求作的三角形．给出示范和作法，让学生模仿，教师可以在黑板上做一次示范，让学生跟着一起操作，并在画完图后，让学生再自己操作一遍．而在下面的作图中，就让学生小组内讨论、交流，通过集体的力量完成，教师再给以一定的指导．2、已知三角形的两角及其夹边，求作这个三角形．已知：线段∠α，∠β，线段c．求作：ΔABC，使得∠A＝∠α，∠B＝∠β，AB＝c．作法：(1)作____________＝∠α；(2)在射线______上截取线段_________＝c；(3)以______为顶点，以_________为一边，作∠______＝∠β，________交_______于点_______．ΔABC就是所求作的三角形．先让学生独立思考，探索作图的过程，对可以自己作出图形的学生，要求他们在小组内交流，用自己的语言表述作图过程．教师要注意提醒学生在作图过程中，是以哪个点为圆心，什么长度为半径作图．3、已知三角形的三边，求作这个三角形．已知：线段a，b，c．求作：ΔABC，使得AB＝c，AC＝b，BC＝a．在完成三个作图后，要鼓励学生比较各自所作的三角形，利用重合等直观的方法观察所作的三角形是否全等．在此机会上，引导学生利用已经获得的三角形全等的条件来说明大家所作的三角形一定是全等的，即说明作法的合理性．课程总结能根据题目给出的条件作出三角形．能口述作图过程．课后作业课本习题1、2。

全等三角形尺规作图xx年xx月xx日CATALOGUE目录•全等三角形基本概念•全等三角形尺规作图基本法则•尺规作图的技巧和方法•尺规作图的实例分析•尺规作图的应用和意义01全等三角形基本概念两个三角形全等是指它们能够完全重合，即三个内角相等且三条边相等。

全等三角形的记号是“≌”，读作“全等形ABCD”或“三角形ABC全等于三角形DEF”。

全等三角形的对应边相等，对应角相等。

全等三角形的对应边上的高相等，对应边上的中线相等，对应角平分线相等。

SSS（Side-Side-Side）：如果三角形的三条边相等，则它们全等。

AAS（Angle-Angle-Side）：如果三角形的两个角相等且这两个角的夹边相等，则它们全等。

ASA（Angle-Side-Angle）：如果三角形的两个角相等且其中一个角的对边相等，则它们全等。

SAS（Side-Angle-Side）：如果三角形的两条边相等且这两条边的夹角相等，则它们全等。

全等三角形的判定方法02全等三角形尺规作图基本法则无刻度直尺只限制长度测量，无法进行面积、角度等测量。

圆规可以用来画圆和圆弧，也可以用来复制图形。

尺规作图的基本概念直接法通过圆规和无刻度直尺，直接画出全等三角形。

间接法通过画出一个三角形，再使用圆规和无刻度直尺，间接画出全等三角形。

全等三角形的尺规作图方法画出三角形使用圆规，以点A为圆心，以AB为半径画圆弧，得到点C；再以点B为圆心，以AB为半径画圆弧，得到点D；连接CD得到三角形ABC。

确定两个已知点确定两个已知点A和B，并连接两点得到线段AB。

判断全等通过比较AC和BC的长度，可以判断三角形ABC和三角形DEF是否全等。

作图步骤03尺规作图的技巧和方法1作图技巧23明确要画的图形，了解所需条件和限制条件。

确定作图目标根据已知条件逐步推导，按照顺序将图形画出来。

画图步骤检查画出的图形是否符合题目要求，确保准确性。

检验作图结果根据等边三角形的性质，通过平分已知角度或边长即可得到三个等边三角形。

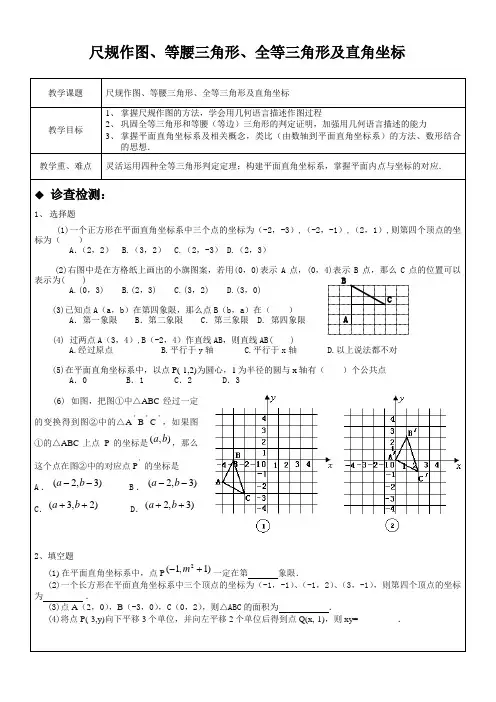
尺规作图、等腰三角形、全等三角形及直角坐标教学课题尺规作图、等腰三角形、全等三角形及直角坐标教学目标1、 掌握尺规作图的方法，学会用几何语言描述作图过程2、 巩固全等三角形和等腰（等边）三角形的判定证明，加强用几何语言描述的能力3、 掌握平面直角坐标系及相关概念，类比（由数轴到平面直角坐标系）的方法、数形结合的思想． 教学重、难点灵活运用四种全等三角形判定定理；构建平面直角坐标系，掌握平面内点与坐标的对应．◆ 诊查检测：1、 选择题(1)一个正方形在平面直角坐标系中三个点的坐标为（-2，-3）,（-2，-1）,（2，1）,则第四个顶点的坐标为（ ）A ．（2，2） B.（3，2） C.（2，-3） D.（2，3）(2)右图中是在方格纸上画出的小旗图案，若用(0，0)表示A 点，(0，4)表示B 点，那么C 点的位置可以表示为( )A.(0，3)B.(2，3)C.(3，2)D.(3，0)(3)已知点A （a ，b ）在第四象限，那么点B （b ，a ）在（ ）A ．第一象限B ．第二象限C ．第三象限 D. 第四象限(4) 过两点A （3，4）,B （-2，4）作直线AB ，则直线AB( )A.经过原点B.平行于y 轴C.平行于x 轴D.以上说法都不对(5)在平面直角坐标系中，以点P(-1,2)为圆心，1为半径的圆与x 轴有（ ）个公共点A ．0B ．1C ．2D ．3(6) 如图，把图①中△ABC 经过一定的变换得到图②中的△A 'B 'C '，如果图①的△ABC 上点P 的坐标是),(b a ，那么这个点在图②中的对应点P '的坐标是A ．)3,2(--b aB ．)3,2(--b aC ．)2,3(++b aD ．)3,2(++b a2、填空题(1) 在平面直角坐标系中，点P)1,1(2+-m 一定在第 象限． (2)一个长方形在平面直角坐标系中三个顶点的坐标为（-1，-1）、（-1，2）、（3，-1），则第四个顶点的坐标为 ． (3)点A （2，0），B （-3，0），C （0，2），则△ABC 的面积为 ．(4)将点P(-3,y)向下平移3个单位，并向左平移2个单位后得到点Q(x,-1)，则xy=_________．A B C3、在所给的图中按所给的语句画图:①连结线段BD; A②过A、C画直线AC；③延长线段AB；④反向延长线段AD． C DE4、如图，使用圆规和直尺分别画出∠AOB和∠BOC的角平分线OM和ON，并说明作图过程．如果∠MON=68º，那么∠AOC应为多少度？5、如图为风筝的图案．（1）若原点用字母O表示，写出图中点A，B，C的坐标．（2）试求（1）中风筝所覆盖的平面的面积．6、如图，在△ABC中三个顶点的坐标分别为A(-5，0)，B(4，0)，C(2，5)，将△ABC沿x轴正方向平移2个单位长度，再沿y轴沿负方向平移1个单位长度得到△EFG。

第七讲 用尺规作三角形2．基本尺规作图包括：(1)作一条线段等于____________；(2)作一个角等于____________；(3)作一个角的平分线(以后将学到)；(4)作一条线段的垂直平分线(以后将学到)；(5)过一点作已知直线的垂线(以后将学到)．3．利用尺规作三角形，有三种基本类型：(1)已知三角形的两边及其夹角，求作符合要求的三角形，其作图依据是“________”；(2)已知三角形的两角及其夹边，求作符合要求的三角形，其作图依据是“________”；(3)已知三角形的三边，求作符合要求的三角形，其作图依据是“________”．4．已知三边作三角形，用到的基本作图是( )A ．作一个角等于已知角B ．作已知直线的垂线C ．作一条线段等于已知线段D ．作一条线段等于已知线段的和5．如图，已知∠α和线段c ，求作等腰三角形ABC ，使其底角∠B ＝∠α，腰AB ＝c .要求仅用直尺和圆规作图，写出作法，并保留作图痕迹．解：作法如下：(1)作射线BP ，再作∠PBQ ＝∠α；(2)在射线BQ 上截取BA ＝c ；(3)以点A 为圆心，线段c 为半径作弧交射线BP 于点C (除过点B 外)；(4)连接AC .则△ABC 即为所求作的三角形(如图)．6．(中考·咸宁)已知：∠AOB . 求作：∠A ′O ′B ′，使∠A ′O ′B ′＝∠AOB .(1)如图①，以点O 为圆心，任意长为半径画弧，分别交OA ，OB 于点C ，D ；(2)如图②，画一条射线O ′A ′，以点O ′为圆心，OC 长为半径画弧，交O ′A ′于点C ′；(3)以点C ′为圆心，CD 长为半径画弧，与第(2)步中所画的弧交于点D ′；(4)过点D ′画射线O ′B ′，则∠A ′O ′B ′＝∠AOB .根据以上作图步骤，请你说明∠A ′O ′B ′＝∠AOB .解：由作法得OD ＝OC ＝O ′D ′＝O ′C ′，CD ＝C ′D ′.在△OCD 和△O ′C ′D ′中，⎩⎪⎨⎪⎧OC ＝O ′C ′，OD ＝O ′D ′，CD ＝C ′D ′，所以△OCD ≌△O ′C ′D ′(SSS)．所以∠COD ＝∠C ′O ′D ′，即∠A ′O ′B ′＝∠AOB .第七讲用尺规作三角形讲义一、尺规作图1.尺规作图的定义：在几何作图中，把用没有刻度的直尺和圆规作图，简称尺规作图．注意：尺规作图指的是只用没有刻度的直尺和圆规两种工具．2.基本作图：①作一条线段等于已知线段；②作一个角等于已知角；③作一个角的平分线；④作线段的垂直平分线；⑤过一点作已知直线的垂线．二、用尺规作三角形1.已知三角形的两边及其夹角，求作这个三角形.已知：线段a，c，∠α(如图).求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α.作法与示例：(1)作一条线段BC＝a；(2)以B为顶点，以BC为一边，作角∠DBC＝∠α；(3)在射线BD上截取线段BA＝c；(4)连接AC.△ABC就是所求作的三角形.2.已知三角形的两角及其夹边，求作这个三角形.已知：∠α，∠β，线段c(如图).求作：△ABC，使∠A＝∠α，∠B＝∠β，AB＝c.请按照给出的作法作出相应的图形.作法：(1)作∠DAF＝∠α；(2)在射线AF上截取线段AB＝c；(3)以B为顶点，以BA为一边，作∠ABE＝∠β，BE交AD于点C，△ABC就是所求作的三角形.例1如图所示，已知线段a，c和∠α，求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α，根据作图在下面空格中填上适当的文字或字母．(1)如图①所示，作∠MBN＝________；(2)如图②所示，在射线BM上截取BC＝_____，在射线BN上截取BA＝________；(3)连接AC，如图③所示，△ABC就是_________________．例2如图，已知：∠α，∠β＝90°，线段a.求作：Rt△ABC，使∠B＝∠α，∠C＝∠β，BC＝2a.(不写作法，保留作图痕迹)例3如图，已知线段a，b，m，求作△ABC，使BC＝2a，AC＝b，且BC边上的中线AD＝m.几何作图的一般步骤：(1)已知，即将条件具体化；(2)求作，即具体叙述所作图形应满足的条件；(3)分析，即寻找作图方法(通常画出草图)；(4)作法，即根据分析所得的作图方法，作出正式图形，并依次叙述作图过程；(5)说明，即验证所作图形的正确性．其中(3)在草稿纸上进行，(5)通常省略不写．例4如图，△ABC是不等边三角形，DE＝BC，以D，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，则最多可以作出_______个这样的三角形．易错小结如图，已知线段a，b和∠α＝40°，你能作出符合如下要求的唯一三角形吗？AB＝a，BC＝b，∠A＝∠α，若能，写出作法；若不能，请说明理由．。

用尺规作图画三角形的方法
要用尺规作图画三角形，需要三个步骤。

第一步：拿起尺规，准备好你要画的图形，例如画一个三角形。

第二步：在纸张上画一条直线，然后拉出尺规的第一端，以三个不容的刻度作为三角形的三边。

可以先将尺规移动到直线下方，然后将尺规旋转90度，按你想要画的三角形的边缘去分别車每一边，再将点连起来画出三角形。

第三步：最后用铅笔将三角形内部的点全部填满，以完成我们用尺规画三角形的步骤。

总之，用尺规画图画三角形共需三步：第一步是拿起尺规，准备好要画的图形，第二步是在纸上画一条直线，通过旋转尺规来画出三角形的三边，第三步是用铅笔将三角形内部的点全部填满，就可以完成我们用尺规画三角形的步骤了。