投入产出数学模型

投入产出模型投入产出模型是指对于经济系统（这一经济系统可以是一个国家，一个地区，一个行业或一个企业的经济活动）的多部门的投入与产出进行研究，编制投入产出表，并建立其数学模型，称作投入产出模型。

这种将经济系统的投入产出关系编制成投入产出表，建立投入产出模型进行研究的方法叫做投入产出法。

投入产出法是由美国著名经济学家瓦西里·列昂节夫20世纪30年代首先提出的。

最初是由研究一国的国民经济各个产业部门间的联系发展起来的,因此被人们称作部门联系平衡法,又叫产业关联法。

利用投入产出模型对经济活动进行分析和进行经济预测，这是一种重要的经济数量分析，叫做投入产出分析。

投入产出分析的理论基础是第七章我们所介绍的一般均衡理论，主要是对一个国家或一个地区宏观经济的研究。

但随着这一方法的广泛应用，它也可以研究一个部门（行业）的经济活动，一个公司或企业的生产经营活动。

本章将在介绍投入产出模型的基础上，着重介绍投入产出模型在国民经济预测和企业经济预测方面的应用。

第一节投入产出模型的基本形式一、投入产出表所谓投入，是指产品生产所需原材料、辅助材料、燃料、动力、固定资产折旧和劳动力的投入；所谓产出，是指产品生产的总量及其分配使用的方向和数量，包括生产消费（中间产品）、生活消费、积累和净出口等。

生产过程就是投入与产出关系的客观反映，一定时期内产品的产出受投入的影响。

投入与产出的数量关系可以编制成一种矩形的表格表示，即投入产出表。

投入产出表可以按实物形态编制，也可以按价值形态编制。

按实物形态编制的投入产出表叫实物表，按价值形态编制的投入产出表叫价值表，两者基本结构形式是相同的，它们之间只差一个价格因素。

投入产出表按编制的范围不同，可以分作世界投入产出表、国家投入产出表、地区投入产出表、部门投入产出表和企业投入产出表。

这里仅以价值形态的全国表为例介绍投入产出表的结构。

假设把国民经济划分为n 个部分，用1，2，…，n 等号码表示。

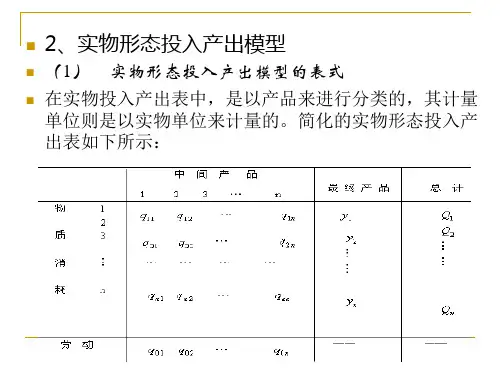
关于农业投入产出的线性回归模型农业投入产出的线性回归模型是利用数学方法来描述农业生产中投入与产出之间的关系，通过建立数学模型对农业投入产出关系作出预测和评估。

线性回归模型指的是将一个或多个自变量与一个因变量之间的关系建立为线性方程形式，并进行拟合。

对于农业投入产出的分析，可以将农业生产的投入因素作为自变量，将农产品产出作为因变量，建立起农业投入产出模型。

Y = α + β1X1 + β2X2 + β3X3 + ... + βkXk其中Y表示农产品产量，X1、X2、X3...Xk表示农业生产中的各项投入因素，如劳动力、农作物种植面积、施肥量、农药使用量等等，α是截距，β1、β2、β3...βk是回归系数，它们表示各项投入因素对产出的影响程度。

在模型中，回归系数βi表示在其他因素不变的情况下，投入因素X1、X2、X3...Xk 每变化一个单位，农产品产量Y会发生的变化量。

比如，如果β1的值为2，表示每增加1个劳动力，农产品产量会增加2个单位。

线性回归模型的建立需要依据已有的数据进行拟合。

为了得到准确的拟合结果，需要采集农业生产的相关数据，进行数据处理和分析，或者通过调查问卷等方式获取数据。

在数据采集和处理时，需要注意采集的数据必须是质量可信的、齐全、准确，并且各项指标间不存在显著的相关性，否则会影响模型的准确性和可靠性。

建立出的线性回归模型可以通过计算农业生产各项投入的系数和截距来确定各项投入因素对农产品产出的影响程度，在实际应用中可以预测未来的生产情况和进行相应的决策。

总之，农业投入产出的线性回归模型是一种定量分析的工具，适用于农业经济领域的生产分析、投资分析、政策制定等方面，它可以帮助我们更准确地理解农业生产中各项投入因素对产出的影响程度，为制定科学的农业生产计划和决策提供参考依据。

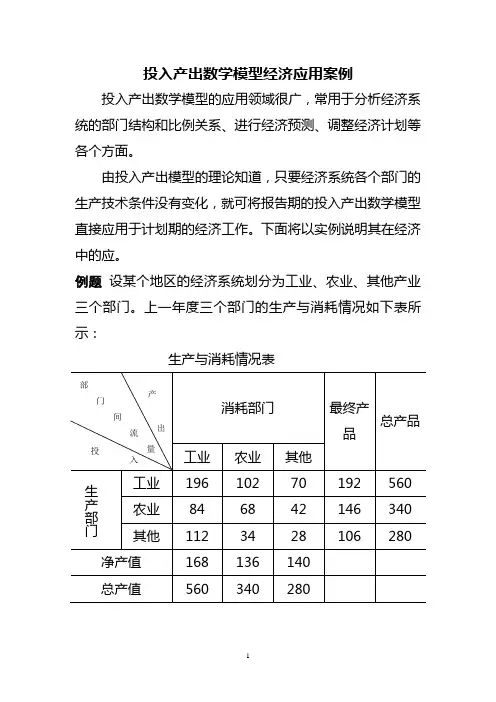
投入产出数学模型经济应用案例投入产出数学模型的应用领域很广，常用于分析经济系统的部门结构和比例关系、进行经济预测、调整经济计划等各个方面。

由投入产出模型的理论知道，只要经济系统各个部门的生产技术条件没有变化，就可将报告期的投入产出数学模型直接应用于计划期的经济工作。

下面将以实例说明其在经济中的应。

例题设某个地区的经济系统划分为工业、农业、其他产业三个部门。

上一年度三个部门的生产与消耗情况如下表所示：生产与消耗情况表假定该系统三个部门的生产技术条件都没有变化，从而该系统的直接消耗系数矩阵不变，由此建立的产品分配方程组和产值构成方程组也不变。

在此基础上，分别分析该系统的报告期投入产出数学模型在计划期经济计划工作方面的下列应用。

（1）在经济预测中的应用假定根据上例所示经济系统的生产发展情况，预计该系统工业、农业、其他产业三个部门的计划期总产品将在报告期总产品的基础上分别增长9%、7%、6%。

由于在生产过程中系统内部存在着复杂的产品消耗关系，故一般说来，各个部门最终产品的增长幅度与总产品的增长幅度并不一致。

试预测该系统最终产品的增长情况。

（2）在制订计划中的应用投入产出数学模型为合理制订经济系统的生产计划提供了一个科学的方法。

根据社会需要确定社会产品的原则，先通过对计划期需要量的预测，确定系统各个部门的最终产品，再利用投入产出数学模型推算出各个部门的总产品，在此基础上编制经济系统计划期的投入产出表，作为安排各个部门计划期生产活动的依据。

现假定通过预测，引例所示经济系统三个部门的计划期最终产品需要量分别为工业部门：1216y=亿元，农业部门：2716y=亿元，其他产业部门：3120y=亿元。

试确定计划期总产品、部门间流量及计划期各部门净产值。

（3）在调整计划中的应用以上介绍了如何根据对最终产品的需求，制订经济系统的生产计划。

但是在执行计划时，可能由于不可预测的原因，导致系统某些部门的最终产品出现缺口(计划产量小于需要量)，或者某些部门的最终产品出现余量(计划产量大于需求量)，从而破坏了经济系统原计划的平衡性。

投入产出模型6.1 投入产出模型投入产出模型对于研究分析国民经济各部门之间的数量依存关系，制定国民经济的计划与规划等都具有十分重要的作用。

根据投入产出模型的原理与方法，现介绍其建模与应用分析的具体方法步骤。

第1节投入产出模型概述投入产出分析是20世纪30年代由美国经济学家瓦。

列昂节夫（W. Leontif）首先提出的，它是研究整个经济系统各部门之间“投入”与“产出”关系的线性模型，一般称为投入产出模型。

国民经济各个部门之间存在着相互依存的关系，每个部门在运转中将其它部门的成品或半成品经过加工（称为投入）变为自己的产品（称为产出），如何根据各部门之间的投入-产出关系，确定各部门的产出水平，以满足社会的需求，是投入产出综合平衡模型研究的问题。

投入产出表投入平衡表简称投入产出表，它是指能够把国民经济各部门之间所有产品的投入与产出关系都表现出来的统计表格。

它是建立投入模型的基础。

主要根据所研究的目的和要求来确定投入产出表的类型。

现以价值型投入产出表为例，如列昂节夫的第一个投入产出表是研究全美国的经济结构的，他编制了全美国十大部门价值型投入产出表。

如表1是一张简化的中国2002年投入产出表，表中国民经济由农业、工业、建筑业、运输邮电业、批零餐饮业和其它服务业6个部门构成，对每个部门有初始投入和总投入，以及外部需求和总产出。

表1中国2002年投入产出表（产值单位：亿元）表中数字均以产值计算，6个部门的横行表示该部门的产品供给各部门生产使用的数量，6个部门的纵列表示该部门生产中消耗的各部门产品的数量。

直接消耗系数直接消耗系数是投入产出应用分析研究最重要的指标。

可在投入产出表的基础上求算直接消耗系数，它可显示出各个部门在生产中的技术经济联系。

如表1中运输邮电部门消耗403亿元工业部门的产品，总产出为1570亿元，于是运输邮电部门的单位产出对工业部门的直接消耗是403/1570=0.257，如此得到的直接小号系数如表2.由于每个部门的总产出等于总投入，计算式将每行数字相应地除以最后一行数字即可。

2.4.2.1 投入产出分析的基本数学模型表2-4-2-1 投入产出表第1产业 第2产业 第3产业 消费 投资 出口 进口 总产出 第1产业d11 d12 d13 FC1 FI1 E1 M1 X1 第2产业d21 d22 d23 FC2 FI2 E2 M2 X2 第3产业d31 d32 d33 FC3 FI3 E3 M3 X3 增加值V1 V2 V3 总产出X1 X2 X3从横列看，ij d 代表的是第i 产业生产过程中对第j 产业产品的需求；从纵列看，ij d 代表的是第j 产业生产过程中i 产业产品的投入量。

定义中间投入率∑i j ij x d/定义中间需求率i ij x d /j ∑定义直接投入系数i ij ij x d a /=定义进口系数)(∑++=j I i C i ij i i f f d m m根据投入产出表的恒等关系，∑=-+++j i i i I i C i ij x m e f f d应用矩阵的形式表示，XM E F F D I C =-+++其中， ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=nn n n d d d d D ........ (1)111，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=C n C C f f F ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=I n I I f f F ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n e e E ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n m m M ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n x x X ...1 同时根据ij ij m a ,的定义，)](**[I C F A I C F F M AX M E F F AX X ++-+++=其中⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=nn n n a a a a A .....................1111，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==n F A m m m M M ..000.00000.000..00..021经过运算后，[][]G *B E )F )(F M -(I *)A M -(I -I X I C F -1A =++=其中 []-1A )AM -(I -I B =,E])F )(F M -[(I G I C F ++= 起元素为ij b， 定义平均关联度∑∑i j ij b 1n 1 定义感应系数∑∑∑j )1/(i jij ij b n b 定义影响力系数∑∑∑ii j ij ij b n b )1/(对X 的结果进一步分解,[][][]BEBF BF E *)A M -(I -I F *)M -(I *)A M -(I -I F *)M -(I *)A M -(I -I X DI DC -1A I F -1A C F -1A ++=++= 算式表明了产出X 与各个部分的关系。

投入产出模型投入产出模型是指对于经济系统（这一经济系统可以是一个国家，一个地区，一个行业或一个企业的经济活动）的多部门的投入与产出进行研究，编制投入产出表，并建立其数学模型，称作投入产出模型。

这种将经济系统的投入产出关系编制成投入产出表，建立投入产出模型进行研究的方法叫做投入产出法。

投入产出法是由美国著名经济学家瓦西里·列昂节夫20世纪30年代首先提出的。

最初是由研究一国的国民经济各个产业部门间的联系发展起来的,因此被人们称作部门联系平衡法,又叫产业关联法。

利用投入产出模型对经济活动进行分析和进行经济预测，这是一种重要的经济数量分析，叫做投入产出分析。

投入产出分析的理论基础是第七章我们所介绍的一般均衡理论，主要是对一个国家或一个地区宏观经济的研究。

但随着这一方法的广泛应用，它也可以研究一个部门（行业）的经济活动，一个公司或企业的生产经营活动。

本章将在介绍投入产出模型的基础上，着重介绍投入产出模型在国民经济预测和企业经济预测方面的应用。

第一节投入产出模型的基本形式一、投入产出表所谓投入，是指产品生产所需原材料、辅助材料、燃料、动力、固定资产折旧和劳动力的投入；所谓产出，是指产品生产的总量及其分配使用的方向和数量，包括生产消费（中间产品）、生活消费、积累和净出口等。

生产过程就是投入与产出关系的客观反映，一定时期内产品的产出受投入的影响。

投入与产出的数量关系可以编制成一种矩形的表格表示，即投入产出表。

投入产出表可以按实物形态编制，也可以按价值形态编制。

按实物形态编制的投入产出表叫实物表，按价值形态编制的投入产出表叫价值表，两者基本结构形式是相同的，它们之间只差一个价格因素。

投入产出表按编制的范围不同，可以分作世界投入产出表、国家投入产出表、地区投入产出表、部门投入产出表和企业投入产出表。

这里仅以价值形态的全国表为例介绍投入产出表的结构。

假设把国民经济划分为n 个部分，用1，2，…，n 等号码表示。