投入产出数学模型

投入产出模型投入产出模型是指对于经济系统（这一经济系统可以是一个国家，一个地区，一个行业或一个企业的经济活动）的多部门的投入与产出进行研究，编制投入产出表，并建立其数学模型，称作投入产出模型。

这种将经济系统的投入产出关系编制成投入产出表，建立投入产出模型进行研究的方法叫做投入产出法。

投入产出法是由美国著名经济学家瓦西里·列昂节夫20 世纪30年代首先提出的。

最初是由研究一国的国民经济各个产业部门间的联系发展起来的,因此被人们称作部门联系平衡法,又叫产业关联法。

利用投入产出模型对经济活动进行分析和进行经济预测，这是一种重要的经济数量分析，叫做投入产出分析。

投入产出分析的理论基础是第七章我们所介绍的一般均衡理论，主要是对一个国家或一个地区宏观经济的研究。

但随着这一方法的广泛应用，它也可以研究一个部门（行业）的经济活动，一个公司或企业的生产经营活动。

本章将在介绍投入产出模型的基础上，着重介绍投入产出模型在国民经济预测和企业经济预测方面的应用。

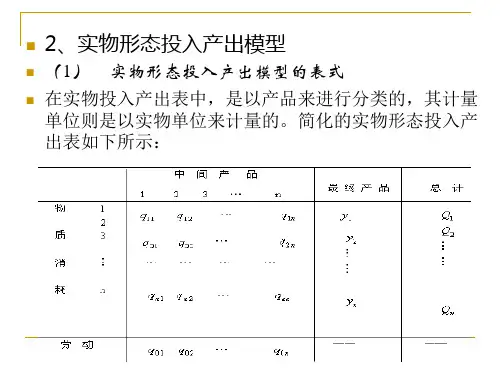
第一节投入产出模型的基本形式一、投入产出表所谓投入，是指产品生产所需原材料、辅助材料、燃料、动力、固定资产折旧和劳动力的投入；所谓产出，是指产品生产的总量及其分配使用的方向和数量，包括生产消费（中间产品）、生活消费、积累和净出口等。

生产过程就是投入与产出关系的客观反映，一定时期内产品的产出受投入的影响。

投入与产出的数量关系可以编制成一种矩形的表格表示，即投入产出表。

投入产出表可以按实物形态编制，也可以按价值形态编制。

按实物形态编制的投入产出表叫实物表，按价值形态编制的投入产出表叫价值表，两者基本结构形式是相同的，它们之间只差一个价格因素。

投入产出表按编制的范围不同，可以分作世界投入产出表、国家投入产出表、地区投入产出表、部门投入产出表和企业投入产出表这里仅以价值形态的全国表为例介绍投入产出表的结构。

假设把国民经济划分为n个部分，用1，2，⋯，n 等号码表示。

投入产出数学模型经济应用案例投入产出数学模型的应用领域很广，常用于分析经济系统的部门结构和比例关系、进行经济预测、调整经济计划等各个方面。

由投入产出模型的理论知道，只要经济系统各个部门的生产技术条件没有变化，就可将报告期的投入产出数学模型直接应用于计划期的经济工作。

下面将以实例说明其在经济中的应。

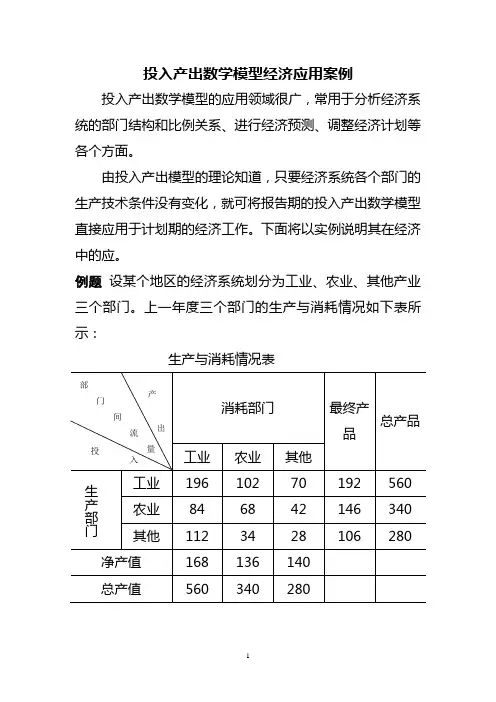
例题设某个地区的经济系统划分为工业、农业、其他产业三个部门。

上一年度三个部门的生产与消耗情况如下表所示：生产与消耗情况表假定该系统三个部门的生产技术条件都没有变化，从而该系统的直接消耗系数矩阵不变，由此建立的产品分配方程组和产值构成方程组也不变。

在此基础上，分别分析该系统的报告期投入产出数学模型在计划期经济计划工作方面的下列应用。

（1）在经济预测中的应用假定根据上例所示经济系统的生产发展情况，预计该系统工业、农业、其他产业三个部门的计划期总产品将在报告期总产品的基础上分别增长9%、7%、6%。

由于在生产过程中系统内部存在着复杂的产品消耗关系，故一般说来，各个部门最终产品的增长幅度与总产品的增长幅度并不一致。

试预测该系统最终产品的增长情况。

（2）在制订计划中的应用投入产出数学模型为合理制订经济系统的生产计划提供了一个科学的方法。

根据社会需要确定社会产品的原则，先通过对计划期需要量的预测，确定系统各个部门的最终产品，再利用投入产出数学模型推算出各个部门的总产品，在此基础上编制经济系统计划期的投入产出表，作为安排各个部门计划期生产活动的依据。

现假定通过预测，引例所示经济系统三个部门的计划期最终产品需要量分别为工业部门：1216y=亿元，农业部门：2716y=亿元，其他产业部门：3120y=亿元。

试确定计划期总产品、部门间流量及计划期各部门净产值。

（3）在调整计划中的应用以上介绍了如何根据对最终产品的需求，制订经济系统的生产计划。

但是在执行计划时，可能由于不可预测的原因，导致系统某些部门的最终产品出现缺口(计划产量小于需要量)，或者某些部门的最终产品出现余量(计划产量大于需求量)，从而破坏了经济系统原计划的平衡性。

国民经济中投⼊产出模型分析国民经济中投⼊产出模型分析投⼊产出理论是研究国民经济各部门联系平衡的⼀种数学⽅法。

整个国民经济是⼀个由许多经济部门组成的有机整体，各部门有密切的联系。

假定整个国民经济分成⼏个物质⽣产部门，每个部门都有双重⾝份，⼀⽅⾯作为⽣产部门以⾃⼰的产品分配给其他部门，另⼀⽅⾯，各个部门在⽣产过程中也要消耗其他部门的产品。

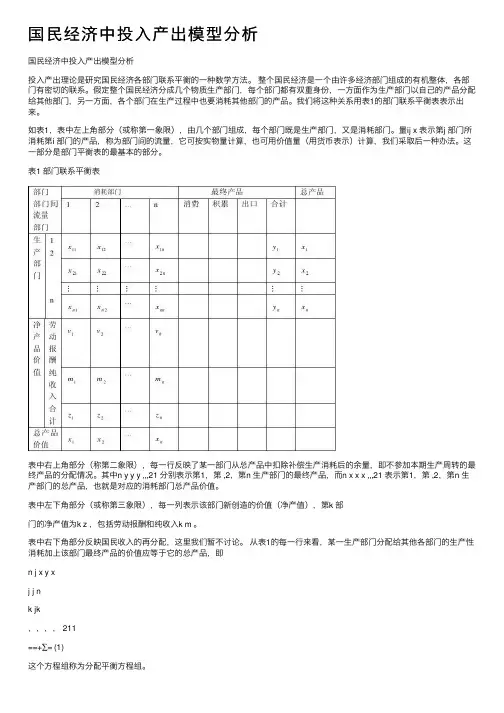
我们将这种关系⽤表1的部门联系平衡表表⽰出来。

如表1，表中左上⾓部分（或称第⼀象限），由⼏个部门组成，每个部门既是⽣产部门，⼜是消耗部门。

量ij x 表⽰第j 部门所消耗第i 部门的产品，称为部门间的流量，它可按实物量计算，也可⽤价值量（⽤货币表⽰）计算，我们采取后⼀种办法。

这⼀部分是部门平衡表的最基本的部分。

表1 部门联系平衡表表中右上⾓部分（称第⼆象限），每⼀⾏反映了某⼀部门从总产品中扣除补偿⽣产消耗后的余量，即不参加本期⽣产周转的最终产品的分配情况。

其中n y y y ,,,21 分别表⽰第1，第 ,2，第n ⽣产部门的最终产品，⽽n x x x ,,,21 表⽰第1，第 ,2，第n ⽣产部门的总产品，也就是对应的消耗部门总产品价值。

表中左下⾓部分（或称第三象限），每⼀列表⽰该部门新创造的价值（净产值），第k 部门的净产值为k z ，包括劳动报酬和纯收⼊k m 。

表中右下⾓部分反映国民收⼊的再分配，这⾥我们暂不讨论。

从表1的每⼀⾏来看，某⼀⽣产部门分配给其他各部门的⽣产性消耗加上该部门最终产品的价值应等于它的总产品，即n j x y xj j nk jk，，，， 211==+∑= (1)这个⽅程组称为分配平衡⽅程组。

从表1的每⼀列来看，每⼀个消耗部门消耗其他各部门的⽣产性消耗加上该部门新创造的价值等于它的总产品的价值，即n j x z xj j nk kj，，，， 211==+∑= (2)这个⽅程组称为消耗平衡⽅程组。

由（1）、（2）易得∑∑===nj jnj j zy 11(3)即各部门最终产品的总和等于各部门新创造价值的总和（即国民收⼊）。

2.4.2.1 投入产出分析的基本数学模型表2-4-2-1 投入产出表第1产业 第2产业 第3产业 消费 投资 出口 进口 总产出 第1产业d11 d12 d13 FC1 FI1 E1 M1 X1 第2产业d21 d22 d23 FC2 FI2 E2 M2 X2 第3产业d31 d32 d33 FC3 FI3 E3 M3 X3 增加值V1 V2 V3 总产出X1 X2 X3从横列看，ij d 代表的是第i 产业生产过程中对第j 产业产品的需求；从纵列看，ij d 代表的是第j 产业生产过程中i 产业产品的投入量。

定义中间投入率∑i j ij x d/定义中间需求率i ij x d /j ∑定义直接投入系数i ij ij x d a /=定义进口系数)(∑++=j I i C i ij i i f f d m m根据投入产出表的恒等关系，∑=-+++j i i i I i C i ij x m e f f d应用矩阵的形式表示，XM E F F D I C =-+++其中， ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=nn n n d d d d D ........ (1)111，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=C n C C f f F ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=I n I I f f F ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n e e E ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n m m M ...1，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n x x X ...1 同时根据ij ij m a ,的定义，)](**[I C F A I C F F M AX M E F F AX X ++-+++=其中⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=nn n n a a a a A .....................1111，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==n F A m m m M M ..000.00000.000..00..021经过运算后，[][]G *B E )F )(F M -(I *)A M -(I -I X I C F -1A =++=其中 []-1A )AM -(I -I B =,E])F )(F M -[(I G I C F ++= 起元素为ij b， 定义平均关联度∑∑i j ij b 1n 1 定义感应系数∑∑∑j )1/(i jij ij b n b 定义影响力系数∑∑∑ii j ij ij b n b )1/(对X 的结果进一步分解,[][][]BEBF BF E *)A M -(I -I F *)M -(I *)A M -(I -I F *)M -(I *)A M -(I -I X DI DC -1A I F -1A C F -1A ++=++= 算式表明了产出X 与各个部分的关系。

关于农业投入产出的线性回归模型农业投入产出是农业经济学领域的一个重要课题，农业投入产出的线性回归模型是研究农业生产效益的一种重要分析方法。

本文将就农业投入产出的线性回归模型进行详细的介绍和分析，希望能对读者有所帮助。

我们来解释一下什么是线性回归模型。

线性回归模型是一种用于研究变量之间线性关系的统计方法，它假设自变量（X）和因变量（Y）之间存在线性关系，可以用一条直线来描述这种关系。

线性回归模型的数学形式为Y = a + bX + e，其中a为截距，b为斜率，e 为误差项。

在农业投入产出的线性回归模型中，通常将农业产出作为因变量，而农业投入作为自变量。

农业产出可以用农产品的产量或者经济价值来表示，而农业投入则包括土地、劳动力、资金、投入品等各种投入要素。

通过建立农业投入产出的线性回归模型，我们可以分析不同投入要素对农业产出的影响程度，进而为农业生产提供科学的指导。

接着，我们来介绍一下如何建立农业投入产出的线性回归模型。

我们需要收集相关数据，包括不同地区、不同作物或畜禽的产量、投入要素的数量和价值等数据。

然后，我们可以利用统计软件进行回归分析，得到回归方程的参数估计值。

通过检验回归方程的拟合优度和参数的显著性，来判断回归模型的适用性和可信度。

在实际应用中，农业投入产出的线性回归模型可以帮助农业生产者和政策制定者做出合理的决策。

我们可以根据回归方程的斜率来分析不同投入要素对产出的影响程度，从而优化投入结构，提高产出效益。

我们还可以通过回归分析的结果来评估不同农业政策对产出的影响，为政策的制定和调整提供科学依据。

农业投入产出的线性回归模型还可以用于预测未来的产出水平，帮助农业生产者做出合理的生产规划和决策。

需要指出的是，农业投入产出的线性回归模型也存在一些局限性。

线性回归模型假设自变量和因变量之间存在线性关系，但在现实中可能存在非线性关系。

当数据不符合线性回归模型的假设时，就需要采用其他回归模型进行分析。