高中物理竞赛复赛专题:角动量及其守恒定律
- 格式:ppt
- 大小:1.55 MB
- 文档页数:2





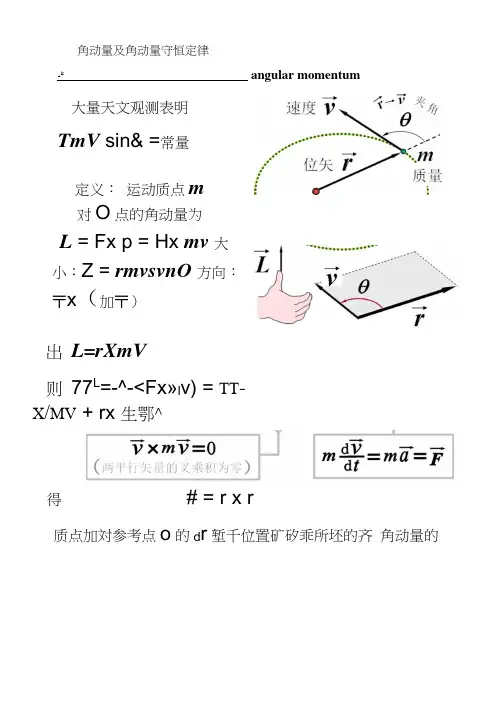
角动量及角动量守恒定律-k大量天文观测表明TmV sin& =常量定义:运动质点m对O点的角动量为L = Fx p = Hx mv 大小:Z = rmvsvnO 方向:〒x(加〒)出L=rXmV则77L=-^-<Fx»l v) = TT-X/MV + rx 生鄂^得# = r x r质点加対参考点o的d r堑千位置矿矽乖所坯的齐角动量的angular momentum吋间变化率莎"矢量尸乂来合外力炉/ -> 二二—F ................. ^-■■■■•.. ... ..... —-亠一亠g ^ ■■■I ■川工= 一二_一】大小M—FYsmG =Fd即力北Af = F X F方向垂直于天亓所决定的平面,出右螺旋法则定指向。
得质点m対给定参考点o的角动量的时I'川变化率=7 x F -M 所受的介外力矩称为质点的角动量龙理的微分形式如果各分力与。
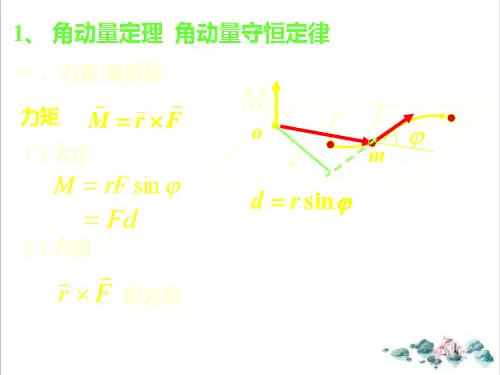
点共面,力矩只含止、反两种方向。
可设顺时针为止向,用代数法求合力矩9质点的角动量守恒定律根据质点的角动量定理^=M ( M=r x F)若M=r x F =0则帶=0即L =常矢量当质点加所受的合外力对某参考点0的力雪历为零时,质点对该点的角动量的时间变化率豁为零,即质点对该点的角动量L守恒。
称为质点的角动量守恒定律若质点所受的合外力的方向始终通过参考点,其角动量守恒,如行星绕太阳运动,以及微观粒子中与此类似的运动模型,服从角动量守恒定律。
质点系的角动量dZ _^T7质点受:外力的时间变化率^dT~i Mi外矩的矢量和 称为 质’点:条旳角动量定瑾微分形式由菲=干莎外=図 j 匸。
"=!z odL =K-Ko 若 M = O 贝!J ZT = Lo 或 L =恒矢量当质点系所受的合外力矩为零时,苴角动量守恒。
.of angular :of partical systei 0 “点白勺箱勻云力质点系的角动量V 2Z =孚 L*=S Af XW/Vzi各质点对给定参考点的角动量的矢量和•丙恵济旳加动垦走翼 将 三=号乙=孚耳厉对时间求导#=?#=? [^=耳[vi^miVi +A ; x/w/fl/J+ A} x 用■=耳[右x Fi 内 +右x 尺外]得=另M i 内+三M ,外=E M i 外=s dr X7M/P/ + 不X 哥-(加了厉)] 某给定 O参考点尺rj dW1r 2m2二见内 用内F L 外内力矩在求矢 量和时成对相消惯性系中某给定参考点/Mi我国第i颗人造卫星沿椭圆轨道运动,地球的中心O为该椭圆的一个焦点•已知地球半径R=6378 kin,卫星与地]fli的最近距离Zi=439km, 与地Ifli的最远距离/2=2384 km・若卫星在近地点A\的速度s=8.1 km-s,则卫星在远地点Ai 的速度s= _____________________ .1.如木题图,一质最为m的质点白由降落,在某时刻具有速度v。

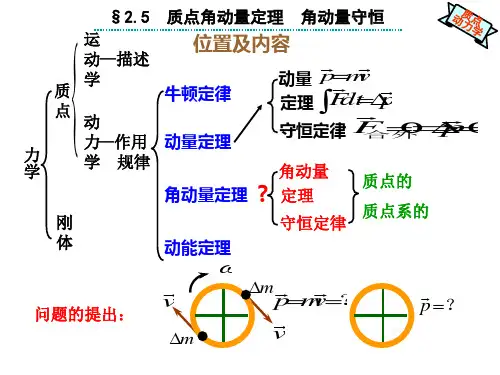

“角动量及角动量守恒定律的应用角动量(angular momentum) 在物理学中是与物体到原点的位移和动量相关的物理量。
概念:转动物体的转动惯量(rotational inertia) 和角速度(angular velocity) 的乘积叫做它的角动量。
L = IωI 是转动惯量,ω(欧米伽)是角速度。
角动量在经典力学中表示为到原点的位移和动量的叉乘,通常写做L 。
角动量是矢量。
L= r×p其中,r表示质点到旋转中心(轴心)的距离(可以理解为半径),L表示角动量。
p 表示动量。
角动量的方向:角动量是r(参考点到质点的距离矢量)叉乘动量,是两个矢量的叉乘,在右手坐标系里遵循右手螺旋法,即右手四指指向r的方向,转过一个小于180度的平面角后四指指向动量的方向,则大拇指所指的方向就是角动量的方向。
在不受外力矩作用时,体系的角动量是守恒的。
角动量在量子力学中与角度是一对共轭物理量。
角动量是一种特殊的动量,它的大小取决于转动的速率和转动物体的质量分布。
角动量守恒定律(conservation of angular momentum,law of)物理学的普遍定律之一。
反映质点和质点系围绕一点或一轴运动的普遍规律。
反映不受外力作用或所受诸外力对某定点(或定轴)的合力矩始终等于零的质点和质点系围绕该点(或轴)运动的普遍规律。
例如一个在有心力场中运动的质点,始终受到一个通过力心的有心力作用,因有心力对力心的力矩为零,所以根据角动量定理,该质点对力心的角动量守恒。
因此,质点轨迹是平面曲线,且质点对力心的矢径在相等的时间内扫过相等的面积。
如果把太阳看成力心,行星看成质点,则上述结论就是开普勒行星运动三定律之一。
一个不受外力或外界场作用的质点系,其质点之间相互作用的内力服从牛顿第三定律,因而质点系的内力对任一点的主矩为零,从而导出质点系的角动量守恒。
如质点系受到的外力系对某一固定轴之矩的代数和为零,则质点系对该轴的角动量守恒。
