2020年4月9日四川省德阳市高2020届高2017级高中2017 级德阳二诊考试理科综合试题化学参考答案

德阳市高中2017级 二诊 试题理综生物部分参考答案与评分标准㊀㊀选择题(每小题6分,共36分)题号123456答案D B A B D A㊀㊀29.(7分)(1)形成纺锤体(1分)(2)核仁(1分)㊀㊀染色质(体)(1分)(3)①2mL 生理盐水(2分)②探究紫杉醇能否通过抑制癌细胞微管的形成来抑制癌细胞的增殖(探究紫杉醇抑制癌细胞增值的机理)(2分)30.(10分)(1)促进和抑制(2分)(2)与雌激素竞争结合雌激素受体(2分)(3)有氧呼吸减弱,无氧呼吸增强(2分,只答 有氧呼吸减弱 得1分;只答 无氧呼吸增强 得2分)㊀㊀乳酸(2分)(4)抑制无氧呼吸的(2分,只答 促进有氧呼吸 得1分)31.(12分)(1)显性(2分)㊀㊀让60株早熟豌豆亲本分别自交,分株收获并保存种子(2分);再分别播种每株植株所结的种子,若所得植株都是早熟的,则这些植株所结豌豆即为纯种的早熟豌豆种子(2分)(2)让偶然出现的那一株矮茎植株自交,在水肥等环境条件相同且适宜的条件下播种,观察子代的表现和比例(2分)㊂若子代全为矮茎,则偶然出现矮茎的原因是由基因突变造成的(2分);若子代出现高茎和矮茎的性状分离,且分离比接近3:1,则偶然出现矮茎的原因是环境因素造成的(2分))页2共(㊀㊀页1第案答分部物生综理级7102高德阳二诊32.(10分)(1)生物群落演替(2分)㊀㊀物质和能量(2分)㊀㊀结构与功能(2分)(2)植物的枯枝落叶,动物的遗体与粪便(2分)(3)提高生物多样性的价值和生态系统的生态㊁社会㊁经济效益(稳定性)(合理即可,2分)37.ʌ生物 选修1:生物技术实践ɔ(15分)(1)颜色㊁形状㊁大小(2分)㊀㊀圆褐固氮菌是好氧细菌需要氧气,且还需要空气中的氮气作为氮源(2分)(2)设置一个接种等量无菌水(或未接种)的空白培养基(2分)㊀㊀判断实验操作过程中是否被杂菌污染(2分)㊀㊀有一个杂菌和一个圆褐固氮菌连在一起(一个圆褐固氮菌分裂为两个后,一个子代细菌发生了基因突变),形成了一个菌落(3分)(3)酶既能与反应物接触又能与产物分离,固定在载体上的酶还可以被反复利用(2分)㊀㊀固定化细胞(2分)38.ʌ生物 选修3:现代生物科技专题ɔ(15分)略)页2共(㊀㊀页2第案答分部物生综理级7102高德阳二诊。

德阳市高中 2020届“二诊”考试语文试卷说明:1.本试卷分第Ⅰ卷和第Ⅱ卷,共10页。

考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效。

考试结束后,将答题卡交回。

2.本试卷满分150分,150分钟完卷。

第Ⅰ卷 (阅读题)一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。

诗人的孤独感空间和时间的扩大使原本定位在稳定的农业田园文化的汉文学,忽然被放置到与游牧民族关系较为密切的流浪文化当中。

我们从李白身上看到很大的流浪感,不止是李白,唐代诗人最大的特征几乎都是流浪。

在流浪的过程中,生命的状态与家、农业家族的牵连性被切断了,孤独感有一部分就来源于不再跟亲属直接联系在一起的状态。

在“安史之乱”之前,李白与王维都有很大的孤独感,都在面对绝对的自我。

在整个汉语文学史上,面对自我的机会非常少,因为我们从小到大的环境,要面对父亲、母亲、哥哥、姐姐、太太、孩子,其实是生活在一个充满人的情感联系的状态里。

我们不要忘记人情越丰富,自我就越少。

我们读唐诗时,能感受到那种快乐,是因为这一次自我真正跑了出来。

李白是彻头彻尾地面对自我。

在他的诗里面读不到孩子、太太,甚至连朋友都很少,他描述他跟宇宙的对话:“五岳寻仙不辞远,一生好入名山游。

”就是为了要成为仙人,在五个最有名的山里跑来跑去。

李白的诗里面一直讲他在找“仙”,“仙”是什么?其实非常抽象,我觉得这个“仙”,是他一个完美的自我。

只有走到山里去,他才比较接近那个完美的自我。

到最后他也没有找到,依旧茫然,可是他不要再回到人间。

因为回到人间,他觉得离他想要寻找的完美自我更遥远。

他宁可是孤独的,因为在孤独里他还有自负;如果他回来,他没有了孤独,他的自负也就会消失。

李白一直在天上和人间之间游离。

他是从人间出走的一个角色,先是感受到巨大的孤独感;然后去寻找一个属于“仙人”的完美性,可是他并没有说他找到了,大部分时候他有一种茫然。

四川省德阳市2020年高三语文“二诊”考试试卷及答案班级：_________ 姓名:_________ 学号：_________ (考试时间60分钟，满分100分，附加题20分)题号1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20附加题总分得分同学们，严肃考风考纪，树立优良学风，祝大家取得优良成绩。

四川省德阳市2017年“二诊”考试语文试题一、现代文阅读(35分)(一)阅读下面的文字,完成1-3题（9分，每小题3分）“知人论世”最早见于《孟子（1分）校外课程有儿童访学课程、春秋主题活动课程和周末学堂。

（1分）（语言连贯、字数1分）四、写作（60分）22．阅读下面的材料，根据要求写一篇不少于800字的文章。

（60分）一名犯有中风病的老人在家中摔倒，老伴跑到50米外的社区求助，社区工作人员立即拨打了120，并提醒说：“你没有第一时间打120，可能已经延误了救治时间，中风病人摔倒后需要的是专业人员的及时救助。

”你对此事有什么看法？要求：综合材料内容及含义，选好角度，确定立意，明确文体，自拟标题；不要套作，不得抄袭。

附文言文参考译文：崔仲方，字不齐，博陵安平人。

崔仲方小时喜欢读书，有文武才干。

十五岁时，周太祖见到他认为不同一般，让他与皇子们一同学习。

当时高祖也在其中，渐渐地彼此之间关系密切起来。

后来以明经做了晋公宇文护的参军，升迁为司玉大夫，与斛斯徵等人一同修撰礼律。

后来因为建立军功，被授予平东将军，赏赐石城县男爵位，世禄封地三百户。

当时周武帝暗地里有灭齐的志向，崔仲方献上二十条计策，周武帝大为惊奇。

后来与少内史赵芬修改确定规章法度。

不久，跟随周武帝攻打晋州。

周武帝又令崔仲方劝降翼城等四城，都如愿攻下。

被授予仪同，进升爵位范阳县侯。

后来担任行军长史，跟随郯公王轨在吕梁活捉陈将吴明彻，崔仲方计策很多。

宣帝继位后，他被任命为少内史，奉命出使淮南后回来。

适逢宣帝去世，高祖做丞相，与崔仲方相见，握手言欢，十分高兴，崔仲方也诚心归顺。

德阳市高中2017级“二诊”考试数学试卷（理工农医类）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知复数21z i =+　，其中i 为虚数单位，则z =（ ）A.B. C. 2D.2.函数y =A ，集合(){}2log 11B x x =+>，则A B =I （ ） A. {}12x x <≤ B. {}22x x -≤≤ C. {}23x x -<< D. {}13x x << 3.执行如图所示程序框图，若输出的结果为3，则可输入的实数x 值的个数为（ ）A. 1B. 2C. 3D. 4 4.函数()()cos ln x x x x f x e e -=+在[],ππ-图象大致为（ ） A.B. C. D. 的5.要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin 2y x =的图象（ ） A. 向右平移6π个单位 B. 向右平移3π个单位 C. 向左平移3π个单位 D. 向左平移6π个单位 6.二项式52x ⎫-⎪⎭的展开式中，常数项为（ ） A. 80- B. 80 C. 160- D. 1607.已知l 为抛物线24x y =的准线，抛物线上的点M 到l 的距离为d ，点P 的坐标为()4,1，则MP d +的最小值是（ ）A. B. 4 C. 2D. 18.不等式组201230x y y x x y -≥⎧⎪⎪≥⎨⎪+-≤⎪⎩表示的平面区域为Ω，则（ ） A. (),x y ∀∈Ω，23x y +>B. (),x y ∃∈Ω，25x y +>C. (),x y ∀∈Ω，231y x +>-D. (),x y ∃∈Ω，251y x +>- 9.平行四边形ABCD 中，已知4AB =，3AD =，点E 、F 分别满足2AE ED =uu u r uu u r ，DF FC =u u u r u u u r ，且6AF BE ⋅=-u u u r u u u r ，则向量AD u u u r 在AB u u u r 上的投影为（ ）A 2 B. 2- C. 32 D. 32- 10.已知ABC V 的内角A 、B 、C 的对边分别为a 、b 、c ，且60A =︒，3b =，AD 为BC 边上的中线，若72AD =，则ABC V 的面积为（ ） A.B. C. 154D. 11.已知实数0a >，1a ≠，函数()2,14ln ,1x a x f x x a x x x ⎧<⎪=⎨++≥⎪⎩在R 上单调递增，则实数a 的取值范围是（ ） A. 12a <≤ B. 5a < C. 35a << D. 25a ≤≤ .12.ABC V是边长为E 、F 分别为AB 、AC 的中点，沿EF 把AEF V 折起，使点A 翻折到点P 的位置，连接PB 、PC ，当四棱锥P BCFE -的外接球的表面积最小时，四棱锥P BCFE -的体积为（ ）A.B.C.D. 二、填空题：共4小题，每小题5分，共20分.将答案填在答题卡上.13.随着国力的发展，人们的生活水平越来越好，我国的人均身高较新中国成立初期有大幅提高.为了掌握学生的体质与健康现状，合理制定学校体育卫生工作发展规划，某市进行了一次全市高中男生身高统计调查，数据显示全市30000名高中男生的身高ξ（单位：cm ）服从正态分布()2172,N σ，且()17218004P ξ<≤=.，那么该市身高高于180cm 的高中男生人数大约为__________.14.春节期间新型冠状病毒肺炎疫情在湖北爆发，为了打赢疫情防控阻击战，我省某医院选派2名医生，6名护士到湖北A 、B 两地参加疫情防控工作，每地一名医生，3名护士，其中甲乙两名护士不到同一地，共有__________种选派方法.15.已知a 、b 为正实数，直线10x y ++=截圆()()224x a y b -+-=所得的弦长为，则1a ab +的最小值为__________.16.在ABC V 中，B 、C的坐标分别为()-，()，且满足sin sin 2B C A -=，O 为坐标原点，若点P 的坐标为()4,0，则AO AP ⋅u u u r u u u r 的取值范围为__________.三、解答题：解答应写出文字说明、证明过程或演算步骤.17.已知数列{}n a 满足：()12311232222122n n n a a a a n +⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+对一切n *∈N 成立. （1）求数列{}n a 的通项公式；（2）求数列21n n a a +⎧⋅⎫⎨⎬⎩⎭的前n 项和n S . 18.如图，四棱锥P ABCD-底面ABCD 中，ABD △为等边三角形，BCD V 是等腰三角形，且顶角120BCD ∠=︒，PC BD ⊥，平面PBD ⊥平面ABCD ，M 为PA 中点.（1）求证：//DM 平面PBC ；（2）若PD PB ⊥，求二面角C PA B --的余弦值大小.19.贫困人口全面脱贫是全面建成小康社会的标志性指标.党的十九届四中全会提出“坚决打赢脱贫攻坚战，建立解决相对贫困的长效机制”对当前和下一个阶段的扶贫工作进行了前瞻性的部署，即2020年要通过精准扶贫全面消除绝对贫困，实现全面建成小康社会的奋斗目标.为了响应党的号召，某市对口某贫困乡镇开展扶贫工作.对某种农产品加工生产销售进行指导，经调查知，在一个销售季度内，每售出一吨该产品获利5万元，未售出的商品，每吨亏损2万元.经统计A ，B 两市场以往100个销售周期该产品的市场需求量的频数分布如下表：A 市场：B 市场：把市场需求量的频率视为需求量的概率，设该厂在下个销售周期内生产n 吨该产品，在A 、B 两市场同时销售，以X （单位：吨）表示下一个销售周期两市场的需求量，Y （单位：万元）表示下一个销售周期两市场的销售总利润.（1）求200X >的概率；（2）以销售利润的期望为决策依据，确定下个销售周期内生产量190n =吨还是200n =吨?并说明理由.20.已知椭圆C ：()222210x y a b a b+=>>24y x =的焦点F .（1）求椭圆C 的标准方程；（2）O 为坐标原点，过O 作两条射线，分别交椭圆于M 、N 两点，若OM 、ON 斜率之积为45-，求证：MON △的面积为定值.21.已知函数()axf x e x =-（a R ∈，e 为自然对数的底数），()ln 1g x x mx =++. （1）若()f x 有两个零点，求实数a 的取值范围；（2）当1a =时，()()x f x x g x ⎡⎤⎣≥⎦+对任意的()0,x ∈+∞恒成立，求实数m 的取值范围. 22.已知点A 为圆C ：()2211x y -+=上的动点，O 为坐标原点，过()0,4P 作直线OA 的垂线（当A 、O 重合时，直线OA 约定为y 轴），垂足为M ，以O 为极点，x 轴的正半轴为极轴建立极坐标系. （1）求点M 的轨迹的极坐标方程；（2）直线l 的极坐标方程为sin 43πρθ⎛⎫+= ⎪⎝⎭，连接OA 并延长交l 于B ，求OA OB 的最大值.23.已知函数()1f x x =+.（1）求不等式()423f x x ≤--的解集；（2）若正数m 、n 满足2m n mn +=，求证：()()28f m f n +-≥.参考答案一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.D2.A3.C4.A5.D6.A7.B8.D9.C10.B11.D12.D二、填空题：共4小题，每小题5分，共20分.将答案填在答题卡上.13. 300014. 2415. 3+16. ()12,+∞三、解答题：解答应写出文字说明、证明过程或演算步骤.17.（1）()12311232222122n n n a a a a n +⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+Q ①，∴当1n =时，1122a ⋅=，11a ∴=，当2n ≥时，()123112312222222n n n a a a a n --⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+②，①-②得：22n n n a n ⋅=⋅，n a n ∴=，适合11a =，故n a n =；（2）()211111222n n a a n n n n +⎛⎫==- ⎪⋅++⎝⎭， 11111111121324352n S n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-+-+⋅⋅⋅+- ⎪ ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 111112212n n ⎛⎫=+-- ⎪++⎝⎭ ()()()35412n n n n +=++. 18. （1）证明：设AB 中点为N ，连接MN 、DN ，QV ABD 为等边三角形，DN AB ∴⊥，DC CB =Q ，120DCB ∠=︒，30CBD ∴∠=︒，603090ABC ∴∠=︒+︒=︒，即CB AB ⊥，DN AB ⊥Q ，//DN BC ∴，BC ⊂Q 平面PBC ，DN ⊄平面PBC ，//DN ∴平面PBC ，MN Q 为PAB △的中位线，//MN PB ∴，PB ⊂Q 平面PBC ，MN ⊄平面PBC ，//MN ∴平面PBC ，MN Q 、DN 为平面DMN 内二相交直线，∴平面//DMN 平面PBC ，DM ⊂Q 平面DMN ，//DM ∴平面PBC ；（2）设BD 中点为O ，连接AO 、COQV ABD 为等边三角形，BCD V 是等腰三角形，且顶角120BCD ∠=︒AO BD ∴⊥，CO BD ⊥，A ∴、C 、O 共线，PC BD ⊥Q ，BD CO ⊥，PC CO C =I ，PC ，CO ⊂平面PCOBD ∴⊥平面PCO .PO ⊂Q 平面PCOBD PO ∴⊥Q 平面PBD ⊥平面ABCD ，交线为BD ，PO ⊂平面PBDPO ∴⊥平面ABCD .设2AB =，则3AO =在BCD V 中，由余弦定理，得：2222cos BD BC CD BC CD BCD =+-⋅⋅∠又BC CD =Q ，222222cos120BC BC ∴=-⋅︒，CB CD ∴==，CO =， PD PB ⊥Q ，O 为BD 中点，112PO BD ∴==， 建立直角坐标系O xyz -（如图），则C ⎛⎫ ⎪ ⎪⎝⎭，()0,0,1P ，)A ，()0,1,0B .)1,0BA ∴=-u u u r ，)1PA =-u u u r ，设平面PAB 的法向量为(),,n x y z =r ，则，0000y n BA n PA z ⎧-=⋅=⇒⎨⋅=-=⎩u u u v v u u u v v ， 取1x =，则y z ==(n ∴=r ， 平面PAC 的法向量为()0,1,0OB =u u u r ，cos ,7n OB n OB n OB⋅==⋅r u u u r r u u u r r u u u r ， Q 二面角C PA B --为锐角，∴二面角C PA B --的余弦值大小为7. 19.（1）设“A 市场需求量为90，100，110吨”分别记为事件1A ，2A ，3A ，“B 市场需求量为90，100，110吨”分别记为事件1B ，2B ，3B ，则()10.2P A =，()20.5P A =，()30.3P A =，()10.1P B =，)2(0.6P B =，()30.3P B =，()()233233200P X P A B A B A B >=++()()()()()()233233P A P B P A P B P A P B =++0.50.30.30.60.30.30.42=⨯+⨯+⨯=；（2）X 可取180，190，200，210，220，()()111800.20.10.02P X P A B ===⨯=()()21121900.50.10.20.60.17P X P A B A B ==+=⨯+⨯=当190n =时，()()18051020.02190510.02948.()6E Y =⨯-⨯⨯+⨯⨯-=当200n =时，()()()()18052020.021*******.17200510.020.17E Y =⨯-⨯⨯+⨯-⨯⨯+⨯⨯-- 985.3=.9486985.3<Q .，200n ∴=时，平均利润大，所以下个销售周期内生产量200n =吨.20.（1）抛物线24y x =的焦点为()1,0F ， 1c ∴=，5e =Q，5c a ∴=， 5a ∴=，2b =，∴椭圆方程为22154x y +=； （2）（ⅰ）当MN 与x 轴垂直时，设直线MN的方程为：()0x t t t =<<≠ 代入22154x y +=得：,M t ⎛ ⎝，,N t ⎛- ⎝，2122455t k k t-∴⋅==-⋅ 2245455t t -∴-⋅=-， 解得：252t =，12MON S t ∴=⋅⋅=△ （ⅱ）当MN 与x 轴不垂直时，设()11,M x y ，()22,N x y ，MN 的方程为y kx m =+ 由()2222245105200154y kx m k x kmx m x y =+⎧⎪⇒+++-=⎨+=⎪⎩， 由22054k m ∆>⇒+>①1221045km x x k +=-+，212252045m x x k -⋅=+4·5OM ON k k =-Q ， 121245y y x x ∴⋅=-，1212540y y x x ∴+= 即()()22121254550k x x mk x x m +⋅+++= ()2222252010545504545m km k mk m k k -⎛⎫∴+⋅+⋅-+= ⎪++⎝⎭整理得：22254m k =+代入①得：0m ≠MN === O 到MN的距离d =12MON S MN d ∴=△===综上：MON S =△.21.（1）()f x 有两个零点⇔关于x 的方程ax e x =有两个相异实根 由0>ax e ，知0x >()f x ∴有两个零点ln x a x ⇔=有两个相异实根. 令()ln x G x x =，则()21ln x G x x -'=， 由()0G x '>得：0x e <<，由()0G x '<得：x e >，()G x ∴()0,e 单调递增，在(),e +∞单调递减()()max 1G x G e e∴==， 又()10G =Q∴当01x <<时，()0G x <，当1x >时，()0G x >当x →+∞时，()0G x →()f x ∴有两个零点时，实数a 的取值范围为10,e ⎛⎫ ⎪⎝⎭； （2）当1a =时，()xf x e x =-， ∴原命题等价于ln 1x xe x mx ≥++对一切()0,x ∈+∞恒成立 ln 1x x m e x x⇔≤--对一切()0,x ∈+∞恒成立. 令()()ln 10xx F x e x x x =--> ()min m F x ∴≤()222ln ln x xx x e x F x e x x +'=+= 令()2ln xh x x e x =+，()0,x ∈+∞，则 ()2120x h x xe x e x'=++> ()h x ∴在()0,∞+上单增又()10h e =>，1201110e h e e e -⎛⎫=-<-= ⎪⎝⎭ 01,1x e ⎛⎫∴∃∈ ⎪⎝⎭，使()00h x =即0020e n 0l x x x +=① 当()00,x x ∈时，()0h x <，当()0,x x ∈+∞时，()0h x >，即()F x 在()00,x 递减，在()0,x +∞递增，()()000min 00ln 1x x F x F x e x x ∴==-- 由①知0200ln x x ex =- 001ln 000000ln 111ln ln x x x x e e x x x x ⎛⎫=-== ⎪⎝⎭∴ Q 函数()x x xe ϕ=在()0,∞+单调递增001ln x x ∴=即00ln x x =- ()0ln 0min 000011111x x F x e x x x x --∴=--=+-=， 1m ∴≤∴实数m 的取值范围为(],1-∞.22.（1）设M 的极坐标为(),ρθ，在OPM V 中，有4sin ρθ=，∴点M 的轨迹的极坐标方程为4sin ρθ=；（2）设射线OA ：θα=，,22ππα⎛⎫∈- ⎪⎝⎭，圆C 的极坐标方程为2cos ρθ=， 由2cos ρθθα=⎧⎨=⎩得：12cos OA ρα==， 由sin 43πρθθα⎧⎛⎫+=⎪ ⎪⎝⎭⎨⎪=⎩得：24sin 3OB ρα==π⎛⎫+ ⎪⎝⎭，2cos 4sin 3OA OB αα∴=π⎛⎫+ ⎪⎝⎭ 1cos sin 23ααπ⎛⎫=⋅+ ⎪⎝⎭ 1cos sin sin cos cos sin 233αααππ⎛⎫=+ ⎪⎝⎭21sin cos 44ααα=+()1sin 2cos 2188αα=++1sin 243πα⎛⎫=+ ⎪⎝⎭， ,22ππα⎛⎫∈- ⎪⎝⎭Q 242333απππ∴-<+<， ∴当232ππα+=，即12πα=时，maxOA OB ⎛⎫= ⎪ ⎪⎝⎭， OAOB ∴. 23.（1）()423f x x ≤--等价于（Ⅰ）()()11234x x x <-⎧⎨-+--≤⎩或（Ⅱ）()()3121234x x x ⎧-≤≤⎪⎨⎪+--≤⎩或（Ⅲ）()()321234x x x ⎧>⎪⎨⎪++-≤⎩由（Ⅰ）得：123x x x <-⎧⎪⇒∈∅⎨≥-⎪⎩由（Ⅱ）得：3130220x x x ⎧-≤≤⎪⇒≤≤⎨⎪≥⎩由（Ⅲ）得：332222x x x ⎧>⎪⇒<≤⎨⎪≤⎩. ∴原不等式的解集为{}02x x ≤≤；（2）0m >Q ，0n >，2m n mn +=，()()221122224m n m n m n +∴+=⋅≤⨯， 28m n ∴+≥， 当且仅当22m n m n mn =⎧⎨+=⎩，即42m n =⎧⎨=⎩时取等号， ()()212128f m f n m n m n ∴+-=++-+≥+≥， 当且仅当210n -+≤即12n ≥时取等号， ()()28f m f n ∴+-≥.。

德阳市高中2017级 二诊 考试理科综合试卷说明:1.本试卷分为选择题和非选择题两部分,第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共14页㊂考生作答时,须将答案答在答题卡上,在本试卷㊁草稿纸上答题无效㊂考试结束后,将答题卡交回㊂2.本试卷满分300分,150分钟完卷㊂可能用到的相对原子质量:H1C12N14O16Na23S32Cl35.5Mn55Fe56第Ⅰ卷㊀(选择题㊀共126分)一㊁选择题(本题包括13小题,每小题6分,共78分㊂每个小题只有一个∙∙∙∙选项符合题意) 1.许多植物在种子发育过程中会合成大量的脂肪,这些 油脂 积累在细胞内一种被称为 油质体 的结构中,下列有关说法错误的是A.脂肪和淀粉是植物体内常见的储能物质B.单层磷脂分子包裹油滴可以构成油质体C.油质体的形成与内质网有很密切的关系D.油质体中积累的脂肪能参与构成细胞膜2.下列生物学实验中,需要用到染色剂和显微镜的实验是①观察DNA和RNA在细胞中的分布②观察叶肉细胞中的叶绿体③观察口腔上皮细胞中的线粒体④观察根尖分生组织细胞的有丝分裂⑤探究紫色洋葱鳞片叶外表皮细胞的吸水和失水A.①②③⑤B.①③④C.②④⑤D.②③④⑤3.将一株生长正常的绿色植物置于密闭无色透明的玻璃容器内,在一定强度的光照下培养,随培养时间的延长,玻璃容器内CO2浓度的变化趋势不可能是A.一直降低,直至为零B.一直保持稳定,不发生变化C.降低至一定水平时保持相对稳定D.升高至一定水平时保持相对稳定)页41共(页1第㊀诊二综理4.下列关于水稻植株相关激素的叙述正确的是A.生长期水稻植株中细胞分裂素的合成只受相应基因的调控B.水稻植株的同一细胞膜上可能含有多种植物激素的受体C.水稻植株产生的乙烯对其它植物的果实没有催熟作用D.水稻植株患恶苗病的原因是其体内产生了过多的赤霉素5.离体培养的小鼠造血干细胞经紫外线诱变处理后对甘氨酸的吸收功能丧失,其它功能不受影响,且这种特性在细胞多次分裂后仍能保持㊂下列分析正确的是A.造血干细胞产生的这种变异是不可遗传变异B.细胞发生变异后合成蛋白质不再需要甘氨酸C.紫外线诱发了细胞中的ATP合成酶基因突变D.细胞膜上相应载体蛋白缺失或结构发生变化6.‘柳叶刀“近期发表的一项研究指出,新冠肺炎患者病情严重与细胞因子风暴(简称CS)相关㊂病毒入侵机体后,受感染的上皮细胞和免疫细胞产生约15种细胞因子帮助抵御病毒,细胞因子会引起更多免疫细胞透过毛细血管并激活这些免疫细胞,被激活的免疫细胞则会产生更多的细胞因子,即细胞因子风暴(CS)㊂由于肺部毛细血管极为丰富,故血管通透性增加后将产生极其严重的后果,除此以外CS还会引起多种器官的衰竭㊂以下有关新冠肺炎的叙述错误的是A.新冠肺炎患者产生细胞因子风暴(CS)是一个负反馈调节过程B.新冠肺炎患者肺部毛细血管通透性增加会导致肺部组织水肿C.肺炎患者富含毛细血管的器官(如肾脏)也可能受CS损伤D.服用使免疫细胞增殖受阻的药物(如类固醇)可缓解患者的症状7.化学与生活密切相关㊂下列叙述错误的是A.疫苗因未冷藏储运而失效,与蛋白质变性有关B.天然气既是高效清洁的化石燃料,又是重要的化工原料C. 中国天眼 的镜片材料为SiC,属于新型有机非金属材料D.港珠澳大桥水下钢柱镶铝块防腐的方法为牺牲阳极的阴极保护法8.有机物 是制备镇痛剂的中间体㊂下列关于该有机物的说法正确的是A.易溶于水及苯B.所有原子可处同一平面C.能发生氧化反应和加成反应D.一氯代物有5种(不考虑立体异构)9.短周期主族元素W㊁X㊁Y㊁Z的原子序数依次增大㊂其中W的气态氢化物常用作制冷剂;X 原子的核外电子层数与最外层电子数相等;Y主族序数大于W㊂下列说法正确的是A.原子半径:W>X B.最简单氢化物的热稳定性:Y>ZC.工业上通过电解熔融XZ3冶炼X单质D.WO2㊁YO2㊁ZO2均为共价化合物)页41共(页2第㊀诊二综理10.设N A为阿伏加德罗常数的值㊂下列说法正确的是A.4.0g由CO2和SO2组成的混合物中含有的质子数为2N AB.1L0.5mol/L pH=7的CH3COONH4溶液中NH+4数目为0.5N AC.常温下,0.1mol环氧乙烷(O)中含有的共价键数目为0.3N AD.22.4L CO2与足量Na2O2充分反应,转移的电子数目为N A11.下列实验能达到目的的是选项目的实验A验证某气体表现还原性将某气体通入溴水中,溴水褪色B制备少量二氧化硫气体向饱和亚硫酸钠溶液中滴加浓硫酸C制备硅酸胶体向硅酸钠水溶液中逐滴滴加浓盐酸至溶液呈强酸性D配制0.2mol/L的CH3COOH溶液准确量取100mL2mol/L的CH3COOH溶液,加入烧杯中稀释后迅速转移至1000mL容量瓶中,然后加蒸馏水定容12.科学家利用电解NaB(OH)4溶液制备H3BO3的工作原理如下图㊂下列说法中正确的是A.b膜为阳离子交换膜B.N室中,进口和出口NaOH溶液的浓度:a%<b%C.电子从左边石墨电极流出,先后经过a㊁b㊁c膜流向右边石墨电极D.理论上每生成1mol H3BO3,两极室共生成33.6L气体(标准状况)13.tħ时,向20.00mL0.1mol/L二元弱酸H2X溶液中滴入0.1mol/L NaOH溶液,溶液中由水电离出的c水(OH-)的负对数[-lg c水(OH-)]与所加NaOH溶液体积的关系如图所示㊂下列说法中不正确的是A.M点溶液中:c(Na+)>c(HX-)>c(X2-)>c(H2X)B.P点溶液中:c(OH-)-c(H+)=c(HX-)+2c(H2X)C.溶液中c(X2-)c(HX-):M<N<P<QD.水的电离程度:P>N=Q>M,且a=7)页41共(页3第㊀诊二综理二㊁选择题:本题共8小题,每小题6分㊂在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求㊂全部选对得6分,选对但不全的得3分,有选错的得0分㊂14.太阳内部持续不断地发生着4个质子(11H)聚变为1个氦核(42He)的热核反应,核反应方程是411Hң42He+2X,这个核反应释放出大量核能.已知质子㊁氦核㊁X的质量分别为m1㊁m2㊁m3,真空中的光速为c.下列说法中正确的是A.方程中的X表示中子10nB.方程中的X表示电子0-1eC.这个核反应中质量亏损Δm=m1-m2-m3D.这个核反应中释放的核能ΔE=(4m1-m2-2m3)c215.甲㊁乙两车某时刻由同一地点㊁沿同一方向开始做直线运动.甲㊁乙两车的位置x随时间t的变化如图所示,则A.0时刻,甲车速度比乙车小B.t2时刻,甲乙两车速度相等C.0~t1时间内,甲车的平均速度比乙车大D.0~t2时间内,甲车通过的距离大16.两行星A和B各有一颗卫星a和b,卫星的圆轨道接近各自的行星表面,如果两行星质量之比M A︰M B=2︰1,两行星半径之比R A︰R B=1︰2,则两个卫星周期之比T a︰T b为A.1︰4B.4︰1C.1︰2D.2︰117.如图所示,两根相距为L的平行直导轨水平放置,R为固定电阻,导轨电阻不计.电阻阻值也为R的金属杆MN垂直于导轨放置,杆与导轨之间有摩擦,整个装置处在竖直向下的匀强磁场中,磁感应强度大小为B.t=0时刻对金属杆施加一水平外力F作用,使金属杆从静止开始做匀加速直线运动.下列关于通过R的电流I(图A为抛物线)㊁杆与导轨间的摩擦生热Q(图B为抛物线)㊁外力F㊁外力F的功率P随时间t变化的图像中正确的是18.如图所示,物体A㊁B的质量分别为m㊁2m,物体B置于水平面上,B物体上部半圆型槽的半径为R,将物体A从圆槽的右侧最顶端由静止释放,一切摩擦均不计.则A.A㊁B物体组成的系统动量守恒B.A不能到达圆槽的左侧最高点C.A运动到圆槽的最低点时A的速率为23gRD.A运动到圆槽的最低点时B的速率为gR3)页41共(页4第㊀诊二综理19.如图甲所示,一理想变压器原㊁副线圈匝数之比为11︰2,其原线圈两端接入如图乙所示的正弦交流电,副线圈通过电流表与负载电阻R相连.若交流电压表和交流电流表都是理想电表,则下列说法中正确的是A.变压器输入电压的最大值是220VB.电压表的示数是40VC.若电流表的示数为0.50A,变压器的输入功率是20WD.原线圈输入的正弦交变电流的频率是100Hz20.如图所示,上表面光滑的半圆柱体放在水平地面上,一小物块从靠近半圆柱体顶点O的A点,在外力F作用下沿圆弧缓慢下滑到B点,此过程中F始终沿圆弧的切线方向且半圆柱体保持静止状态.下列说法中正确的是A.半圆柱体对小物块的支持力变大B.外力F变大C.地面对半圆柱体的支持力先变大后变小D.地面对半圆柱体的摩擦力先变大后变小21.理论研究表明,无限大的均匀带电平板在周围空间会形成与平面垂直的匀强电场.现有两块无限大的均匀绝缘带电平板正交放置,如图所示,A1B1板两面带正电,A2B2板两面带负电,且两板单位面积所带电荷量相等(设电荷不发生移动).图中直线A1B1和A2B2分别为带正电平面和带负电平面与纸面正交的交线,O点为两交线的交点,C㊁D㊁E㊁F恰好位于纸面内正方形的四个顶点上,且CE的连线过O点.则下列说法中正确的是A.E㊁F两点场强相同B.D㊁F两点电势相同C.U EF=U EDD.在C㊁D㊁E㊁F四个点中电子在F点具有的电势能最大)页41共(页5第㊀诊二综理第Ⅱ卷(非选择题㊀共174分)本卷包括必考题和选考题两部分㊂第22~32题为必考题,每个试题考生都必须做答㊂第33~38题为选考题,考生根据要求做答㊂(一)必考题(共129分)22.(6分)某同学在研究性学习中,利用所学的知识解决了如下问题:一轻弹簧一端固定于某一深度为h=0.15m㊁开口向右的小筒中(没有外力作用时弹簧的另一端也位于筒内),如图甲所示,如果本实验的长度测量工具只能测量出筒外弹簧的长度l,现要测出弹簧的原长l0和弹簧的劲度系数k,该同学通过改变所挂钩码的个数来改变l,作出F-l图线如图乙所示.(1)由此图线可得出弹簧的弹力与伸长量的关系是.(2)弹簧的劲度系数k=N/m,弹簧的原长l0=m.23.(9分)某同学通过实验研究小灯泡的电流与电压的关系.实验器材如图甲所示,现已完成部分导线的连接.(1)实验要求电表的示数从零开始逐渐增大,请按此要求用笔画线代替导线在图甲实物接线图中完成余下导线的连接;(2)某次测量电流表指针偏转如图乙所示,则电流表的示数为A;(3)该同学描绘出小灯泡的伏安特性曲线如图丙所示,根据图像可知小灯泡的电阻随电压增大而(选填 增大 ㊁ 减小 或 不变 ).将该小灯泡直接与电动势为3V㊁内阻为5Ω的电源组成闭合回路,小灯泡的实际功率约为W(保留二位有效数字).)页41共(页6第㊀诊二综理24.(12分)我国将于2022年举办冬奥会,跳台滑雪是其中最具观赏性的项目之一.如图所示,质量m =60kg 的运动员从倾角θ=30ʎ㊁长度L =80m 的滑道AB 的A 处由静止开始匀加速滑下,经过t =8s 到达滑道末端B.为了改变运动员的运动方向,在滑道与起跳台之间用一段弯曲滑道衔接,其中最低点C 处附近是一段以O 为圆心㊁半径R =14m 的圆弧,滑道末端B 与弯曲滑道最低点C 的高度差h =5m,运动员在B ㊁C 间运动时阻力做功W =-1000J,g =10m /s 2.求:(1)运动员在AB 段下滑时受到阻力f 的大小;(2)运动员到达滑道最低点C 时对滑道的压力F N 的大小.25.(20分)如图所示,将一矩形区域abcdef 分为两个矩形区域,abef 区域充满匀强电场,场强为E ,方向竖直向上;bcde 区域充满匀强磁场,磁感应强度为B ,方向垂直纸面向外.be 为其分界线㊂af ㊁bc 长度均为L ,ab 长度为0.75L.现有一质量为m ㊁电荷量为e 的电子(重力不计)从a 点沿ab 方向以初速度v 0射入电场.已知电场强度E =16mv 209eL ,sin37ʎ=0.6,cos37ʎ=0.8.求:(1)该电子从距离b 点多远的位置进入磁场;(2)若要求电子从cd 边射出,所加匀强磁场磁感应强度的最大值;(3)若磁感应强度的大小可以调节,则cd 边上有电子射出部分的长度为多少.26.(14分)某科研课题小组研究利用含H +㊁Zn 2+㊁Mn 2+㊁Fe 2+㊁Fe 3+㊁Cl -㊁SO 2-4的工业废液,制备高纯的ZnO㊁MnO 2㊁Fe 2O 3,设计出如下实验流程:已知:①氢氧化锌沉淀呈白色②氢氧化锰难溶于水③溶液中金属离子沉淀完全时,其浓度ɤ1ˑ10-5mol /L )页41共(页7第㊀诊二综理回答下列问题:(1)向工业废液中加入双氧水,可能观察到的现象有:溶液的颜色发生变化和㊀㊀㊀㊀,其中引起溶液颜色变化的离子方程式为㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(2)第一次调pH 的目的是沉淀Fe 3+㊂检验Fe 3+是否完全沉淀的操作:取少量滤液于洁净试管中,最好加入下列试剂中的㊀㊀㊀㊀(填标号),并观察实验现象㊂a.稀氨水㊀㊀㊀㊀㊀b.KSCN 溶液㊀㊀㊀㊀㊀c.K 3Fe(CN)6溶液(3)第二次调pH 前,科研小组成员在室温下分析此时的溶液,得到相关数据见下表浓度(mol /L)氢氧化物的K sp 开始沉淀的pH 完全沉淀的pH Zn 2+0.12 1.2ˑ10-176.08.1Mn 2+0.10 4.0ˑ10-147.89.8㊀㊀为防止Mn 2+也同时沉淀造成产品不纯,最终选择将溶液的pH 控制为7.5,则此时溶液中Zn 2+的沉淀率为㊀㊀㊀㊀㊀㊀㊂(第二次调pH 前后液体体积的变化忽略不计)(4)已知常温下,K sp (MnS)=3.0ˑ10-14㊁K sp (ZnS)=1.5ˑ10-24㊂在除锌时发生沉淀转化反应为:MnS(s)+Zn 2+(aq) ZnS(s)+Mn 2+(aq),其平衡常数K =㊀㊀㊀㊀㊀㊀㊂(5)沉锰反应在酸性条件下完成,写出反应的离子方程式㊀㊂(6)下列关于沉锰制备高纯MnO 2的说法中,不正确的是㊀㊀㊀㊀(填标号)㊂a.若沉锰反应时加入足量浓盐酸并加热,MnO 2的产率将降低b.若沉锰后进行过滤操作,为了加快过滤速率,不断用玻璃棒搅拌c.若除锌时加入MnS 质量为x g,沉锰反应中锰元素无损失,MnO 2的产量将增加x g 27.(15分)对甲基苯胺可用对硝基甲苯作原料在一定条件制得㊂主要反应及装置如下:H 3C NO 2㊀㊀㊀㊀㊀㊀㊀㊀(Mr =137)Fe HCl ңCH 3NH +3OH -H + CH 3NH 2主要反应物和产物的物理性质见下表:化合物溶解性熔点(ħ)沸点(ħ)密度(g㊃cm -3)对硝基甲苯不溶于水,溶于乙醇㊁苯51.4237.7 1.286对甲基苯胺微溶于水,易溶于乙醇㊁苯43~45200~202 1.046对甲基苯胺盐酸盐易溶于水,不溶于乙醇㊁苯243~245 苯不溶于水,溶于乙醇 5.580.10.874)页41共(页8第㊀诊二综理㊀㊀实验步骤如下:①向三颈烧瓶中加入50mL稀盐酸㊁10.7mL(13.7g)对硝基甲苯和适量铁粉,维持瓶内温度在80ħ左右,同时搅拌回流㊁使其充分反应;②调节pH=7~8,再逐滴加入30mL苯充分混合;③抽滤得到固体,将滤液静置㊁分液得液体M;④向M中滴加盐酸,振荡㊁静置㊁分液,向下层液体中加入NaOH溶液,充分振荡㊁静置;⑤抽滤得固体,将其洗涤㊁干燥得6.1g产品㊂回答下列问题:(1)主要反应装置如上图,a处缺少的装置是㊀㊀㊀㊀㊀㊀㊀㊀㊀(填仪器名称),实验步骤③和④的分液操作中使用到下列仪器中的㊀㊀㊀㊀(填标号)㊂a.烧杯㊀㊀㊀㊀b.漏斗㊀㊀㊀㊀c.玻璃棒㊀㊀㊀㊀d.铁架台(2)步骤②中用5%的碳酸钠溶液调pH=7~8的目的之一是使Fe3+转化为氢氧化铁沉淀,另一个目的是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(3)步骤③中液体M是分液时的㊀㊀㊀层(填 上 或 下 )液体,加入盐酸的作用是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(4)步骤④中加入氢氧化钠溶液后发生反应的离子方程式有㊀㊂(5)步骤⑤中,以下洗涤剂中最合适的是㊀㊀㊀㊀(填标号)㊂a.乙醇㊀㊀㊀㊀b.蒸馏水㊀㊀㊀㊀c.HCl溶液㊀㊀㊀㊀d.NaOH溶液(6)本实验的产率是㊀㊀㊀㊀㊀%㊂(计算结果保留一位小数)28.(14分)处理㊁回收利用CO是环境科学家研究的热点课题㊂回答下列问题:Ⅰ.处理大气污染物CO用于处理大气污染物N2O所发生的反应原理为:CO(g)+N2O(g) CO2(g)+N2(g)㊀әH=-224.0kJ/mol有人提出上述反应可以用 Fe+ 作催化剂㊂其总反应分两步进行:(1)第一步:Fe++N2O FeO++N2;第二步:㊀㊀㊀㊀㊀㊀㊀㊀㊀(写反应方程式)㊂(2)第二步反应不影响总反应达到平衡所用时间,由此推知,第二步反应速率㊀㊀㊀㊀第一步反应速率(填 大于 小于 或 等于 )㊂Ⅱ.合成天然气(SNG)涉及的主要反应原理如下:CO甲烷化:CO(g)+3H2(g) CH4(g)+H2O(g)㊀㊀әH1=-206.2kJ/mol水煤气变换:CO(g)+H2O(g) CO2(g)+H2(g)㊀㊀әH2=-41.2kJ/mol(3)反应CO2(g)+4H2(g) CH4(g)+2H2O(g)的әH=㊀㊀㊀㊀kJ/mol㊂)页41共(页9第㊀诊二综理㊀㊀(4)在一恒容容器中,按照n mol CO和3n mol H2投料发生CO甲烷化反应,测得CO在不同温度下的平衡转化率与压强的关系如右图所示,下列说法正确的是㊀㊀㊀㊀(填标号)㊂A.温度:T1<T2<T3B.正反应速率:v(e)>v(c)>v(b)C.平衡常数:K(a)<K(d)<K(c)D.平均摩尔质量:M(a)>M(b)=M(e)(5)在恒压管道反应器中,按n(H2)︰n(CO)=3︰1通入原料气发生CO甲烷化反应, 400ħ㊁P总为100kPa时反应体系平衡组成如下表所示㊂组分H2CO CH4H2O CO2体积分数φ/%8.50 1.5045.044.0 1.00㊀㊀则该条件下CO的总转化率α=㊀㊀㊀㊀㊂(保留一位小数)(6)将制备的CH4用来组成下图所示燃料电池电解制备N2O5①阳极的电极反应为㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂②理论上制备1mol N2O5,石墨2电极消耗气体的体积为㊀㊀㊀㊀L(标准状况)㊂29.(7分)微管(一种蛋白质纤维)几乎存在于所有的真核细胞内,参与细胞内多种重要结构的构成(如细胞骨架㊁纺锤体等)㊂动物细胞的分裂间期,微管通常是从中心体开始装配的㊂回答下列问题:(1)根据上述材料可知,中心体在动物细胞有丝分裂过程中的作用是㊀㊀㊀㊀㊀㊂(2)细胞骨架的合成与细胞核中的㊀㊀㊀㊀㊀和㊀㊀㊀㊀㊀两种结构有关㊂(3)微管形成抑制剂能抑制细胞微管的形成,从而阻断癌细胞的增殖,剂量越大阻断效果越好;某研究者发现紫杉醇也能抑制癌细胞增殖,同时还进行了如下实验:A组:动物细胞培养液+癌细胞+1mL紫杉醇+1mL生理盐水B组:动物细胞培养液+癌细胞+1mL微管形成抑制剂+1mL生理盐水C组:动物细胞培养液+癌细胞+1mL紫杉醇+1mL微管形成抑制剂D组:动物细胞培养液+癌细胞+㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀①D组横线上应该加入的试剂是:㊀㊀㊀㊀㊀㊂)页41共(页01第㊀诊二综理②进行该探究实验的主要目的是:㊀㊂30.(10分)他莫昔芬(Tam)是一种治疗乳腺癌的药物,但患者长期使用后药效会降低㊂科研人员测定了初次使用Tam的乳腺癌患者的癌细胞(细胞系C)和长期使用Tam的乳腺癌患者的癌细胞(细胞系R)的氧气消耗速率及葡萄糖摄取速率,结果如图所示:请回答:(1)男女均有乳腺,但患乳腺癌的病人几乎都是女性,由此推测:雌激素对乳腺癌细胞生长和凋亡分别起㊀㊀㊀㊀㊀作用㊂(2)临床研究发现:雌激素受体正常的患者使用Tam治疗效果较好,受体异常患者疗效较差㊂这可能是由于Tam进入细胞后会㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀,降低了雌激素的作用㊂(3)由实验结果推测:由于细胞系R的细胞呼吸发生了㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀的变化,从而使葡萄糖摄取速率明显提高㊂验证上述推测的最佳方法是检测并比较细胞系C和R的㊀㊀㊀㊀㊀产生量㊂(4)综合以上研究,长期服用Tam的乳腺癌患者在使用Tam的同时可以服用㊀㊀㊀㊀㊀㊀㊀㊀药物,使Tam的抗癌效果更好㊂31.(12分)豌豆(二倍体自花传粉作物)是遗传育种研究的典型实验材料㊂在一个本来种植晚熟豌豆的大田中,出现了一株早熟的植株,自然条件下将该早熟植株的种子种下去,在长出的80株新植株中只有60株是早熟的㊂请回答:(1)由上述情况可知早熟性状是㊀㊀㊀㊀(显性/隐性)性状㊂以题干中出现的60株早熟豌豆为亲本,如何在两代以内分离得到纯合的早熟豌豆种子?(不使用单倍体育种,写出实验思路即可)㊀㊂(2)现以纯种高茎豌豆和纯种矮茎豌豆杂交,子一代全为高茎,子二代表现为高茎:矮茎= 3:1;重复实验时发现子一代偶然出现了一株矮茎植株㊂为了弄清重复实验时偶然出现的那一株矮茎植株出现的原因是基因突变造成的,还是生长发育过程中水肥等环境因素影响造成的?请设计一个简单的遗传实验进行探究㊂(要求:写出实验方案㊁预期实验结果㊁得出实验结论)㊀㊂)页41共(页11第㊀诊二综理32.(10分)人们可以采用许多恢复生态学技术来治理退化的生态系统,例如分步骤在盐碱化草原种植不同植物,以改造盐碱化草原,并采用生态工程的办法进行生态恢复㊂请回答: (1)恢复生态学主要利用的是㊀㊀㊀㊀㊀㊀㊀㊀㊀理论,并人为增加㊀㊀㊀㊀㊀㊀㊀的投入,从而尽快使生态系统的㊀㊀㊀㊀㊀㊀㊀恢复到(或接近)受干扰前的正常健康状态㊂(2)恢复后的草原动植物种类和数量,土壤中有机物含量均有明显增加㊂土壤有机物的来源有㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(3)采用恢复生态学技术改造盐碱化草原的生态学意义是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(二)选考题:共45分㊂请考生从2道物理题㊁2道化学题㊁2道生物题中每科任选1题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑㊂注意所选题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置做答㊂多答则每学科按所答的第1题评分㊂33.[物理 选修3-3](15分)略34.[物理 选修3-4](15分)(1)(5分)如图所示为半圆形的玻璃砖,C为AB的中点,OOᶄ为过C点的AB面的垂线.a,b两束不同频率的单色可见细光束垂直AB边从空气射入玻璃砖,且两束光在AB面上入射点到C点的距离相等,两束光折射后相交于图中的P点,以下判断正确的是㊀㊀㊀(填正确答案标号,选对1个得2分,选对2个得4分,选对3个得5分,每选错1个扣3分,最低得分为0分)A.在半圆形的玻璃砖中,a光的传播速度小于b光的传播速度B.a光的频率小于b光的频率C.两种色光分别通过同一双缝干涉装置形成的干涉条纹,相邻明条纹的间距a光的较大D.若a,b两束光从同一介质射入真空过程中,a光发生全反射的临界角小于b光发生全反射的临界角E.a光比b光更容易发生衍射现象(2)(10分)如图所示,一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图中的实线所示,此时这列波恰好传播到P点,再经过1.5s,坐标为x=8m的Q点开始起振.求:①该列波的周期T和振源O点的振动方程;②从t=0时刻到Q点第一次达到波峰时,振源O点相对平衡位置的位移y及其所经过的路程s.)页41共(页21第㊀诊二综理㊀㊀35.[化学-选修3:物质结构与性质](15分)Ni 元素在生产㊁生活中有着广泛的应用㊂回答下列问题:(1)基态Ni 原子价层电子的排布式为㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(2)科学家在研究金属矿物质组分的过程中,发现了Cu -Ni -Fe 等多种金属互化物㊂确定某种金属互化物是晶体还是非晶体最可靠的科学方法是对固体进行㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(3)Ni 能与类卤素(SCN)2反应生成Ni(SCN)2㊂Ni(SCN)2中,第一电离能最大的元素是㊀㊀㊀㊀㊀㊀;(SCN)2分子中,硫原子的杂化方式是㊀㊀㊀㊀㊀㊀㊀㊀,σ键和π键数目之比为㊀㊀㊀㊀㊂(4)[Ni(NH 3)6](NO 3)2中,不存在的化学键为㊀㊀㊀㊀(填标号)㊂a.离子键㊀㊀㊀㊀b.金属键㊀㊀㊀㊀c.配位键㊀㊀㊀㊀d.氢键(5)镍合金储氢的研究已取得很大进展㊂①图甲是一种镍基合金储氢后的晶胞结构示意图㊂该合金储氢后,含1mol La 的合金可吸附H 2的数目为㊀㊀㊀㊀㊂②Mg 2NiH 4是一种贮氢的金属氢化物㊂在Mg 2NiH 4晶胞中,Ni 原子占据如图乙的顶点和面心,Mg 2+处于乙图八个小立方体的体心㊂Mg 2+位于Ni 原子形成的㊀㊀㊀㊀㊀㊀㊀㊀(填 八面体空隙 或 四面体空隙 )㊂若晶体的密度为d g /cm 3,Mg 2NiH 4的摩尔质量为M g /mol,则Mg 2+和Ni 原子的最短距离为㊀㊀㊀㊀nm(用含d ㊁M ㊁N A 的代数式表示)㊂36.[化学-选修5:有机化学基础](15分)倍他乐克是一种治疗高血压的药物,其中间体F 合成路线如下: HO O A CuBr 2①ң HO O CH 2Br B CH 3ONa ②ң HO O CH 2OCH 3C H 2/Pd -C ③ң HO CH 2OCH 3DC 3H 5OBr 一定条件④ң O O CH 2OCH 3E 试剂X ⑤ңOOHN H CH 2OCH 3F 回答下列问题:(1)A 的分子式为㊀㊀㊀㊀㊀㊀㊀㊂D 中官能团的名称是㊀㊀㊀㊀㊀㊀㊀㊀㊂)页41共(页31第㊀诊二综理(2)B 与足量NaOH 溶液反应的化学方程式为㊀㊂(3)D ңE 的反应类型为㊀㊀㊀㊀㊀㊀㊂(4)反应⑤加入试剂X 反应后只生成中间体F,则X 结构简式为㊀㊂(5)满足下列条件的C 的同分异构体有㊀㊀㊀㊀种㊂①能发生银镜反应;②与NaOH 溶液反应时,1mol C 最多消耗3mol NaOH;③苯环上只有4个取代基,且直接与苯环相连的烃基处于间位㊂其中核磁共振氢谱有4种不同化学环境的氢,且峰面积比为1︰6︰2︰1的可能是㊀㊀㊀(写结构简式)㊂(6)根据已有知识及题目相关信息,完成以 Br O CH 2OH 和CH 3OH㊁CH 3ONa 为原料制备O CHO 的合成路线流程图(无机试剂任选)㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂37.ʌ生物 选修1:生物技术实践ɔ(15分)圆褐固氮菌能将大气中的氮气转化为氨供自身利用,是异养需氧型的原核生物㊂某同学利用稀释涂布平板法从土壤中分离获得圆褐固氮菌㊂回答下列问题㊂(1)根据菌落的㊀㊀㊀㊀㊀㊀㊀㊀等特征,进行反复分离㊁纯化可以分离得到纯化菌种㊂分离㊁纯化圆褐固氮菌时不能隔绝空气,其原因是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀(答出两点)㊂(2)某同学计划统计土壤样液中圆褐固氮菌的总数,他选用10-4㊁10-5㊁10-6稀释倍数进行涂布,每个稀释倍数下都设置了3个培养皿㊂从无菌操作的角度分析,该同学还应设置的一组对照组是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀,其目的是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂在10-4浓度下一个培养基表面发现:圆褐固氮菌菌落呈黄褐色,而有一个菌落半边呈白色,半边呈黄褐色㊂出现上述现象的可能原因是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊂(3)若用固定化酶技术固定圆褐固氮菌产生的固氮酶,和一般酶制剂相比,其优点是㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀;将冷却后的海藻酸钠溶液与圆褐固氮菌菌液进行混合,通过注射器滴入CaCl 2溶液中,这种技术称为㊀㊀㊀㊀㊀㊂38.ʌ生物 选修3:现代生物科技专题ɔ(15分)略)页41共(页41第㊀诊二综理。

数学二诊( 理工农医类)第1页( 共4 页)函数 f ( x ) = ln( ex e -x cos x + ) 在[ - π,π] 的图象大致为 为了得到函数 y = s i n (2x + π)的图象,可将函数 y = s i n 2x 的图象2. 3四川德阳市2020届高三“ 二诊” 考试数 学 试 卷( 理工农医类)说明:1. 本试卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷 1—2 页,第Ⅱ卷 3—4 页. 考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效. 考试结束后,将答题卡交回. 本试卷满分 150 分,120 分钟完卷.第Ⅰ卷( 选择题 共 60 分)一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知复数 z = 1 2+ i,其中 i 为虚数单位,则 z =A. 5B. 3C. 2D. 2. 函数y = 4 -x 2 的定义域为A ,集合B = {x 则 A ∩ B = A. {x 1 < x ≤ 2} B. {x - 2 ≤ x ≤ 2} C. {x - 2 < x < 3} D. {x 1 < x < 3}log 2(x + 1) > 1} , 3. 执行如图所示的程序框图,若输出的结果为 3,则可输入的实数 x 值的个数为 A. 1 B. x 2 C. 3 D. 44.5. π π π πA. 向右平移 3B. 向左平移3C. 向左平移6D. 向右平移 62数学二诊( 理工农医类)第2页( 共4 页)xM d x - 1x - 1 2 44, 、 , ,12 △ 2 3 , 、 、 , △ , 4444已知 为抛物线 4 的准线 , 点 2 6. 二项式(2- x2)5的展开式中,常数项为7. A. - l 80 x 2= B.y 80 , C. - 160 D. 160(4,1), 则 MP + d 的最小值是A.17⎧⎪2x B. 4 C. 2 D. 1 + 17- y ≥ 0 8. 不等式组⎪y ≥ 1x 表示的平面区域为 Ω,则⎨ ⎪ ⎪⎩x + y - 3 ≤ 0A. ∀( x ,y ) ∈ Ω,x + 2y > 3B. ∃( x ,y ) ∈ Ω,x + 2y > 5C. ∀( x ,y ) ∈ Ω,y + 2 > 3D. ∃( x ,y ) ∈ Ω,y + 2> 5 9. 平行四边形 A B CD 中,已知 A B = 4,A D = 3,点 E 、F 分别满足A →E = 2E →D ,D →F =F →C ,且 A →F ·B →E = - 6,则向量A →D 在A →B 上的投影为A. 2B. - 2C. 3D. - 310. 已知 △ABC 的内角 A 、B 、C 的对边分别为 a 、 2 c ,且 A = 60°,b = 3, 2为 BC 边上的中线,若AD = b 、 AD7 ,则 △ABC 的面积为A. 25 3 C.15{a x,x < 111. 已知实数 a > 0,a ≠ 1,函数 f ( x ) =x 2+ 4x+ a l n x ,x ≥ 1在 R 上单调递增,则实数 a 的取 值范围是A. 1 < a ≤ 2B. a < 5C. 3 < a < 5D. 2 ≤ a ≤ 5. ABC 是边长为 的等边三角形 E F 分别为 AB AC 的中点 沿 EF 把 AEF 折起 使点A 翻折到点 P 的位置 连接 PB PC 当四棱锥 P - BCFE 的外接球的表面积最小时 四棱锥P - BCFE 的体积为 A.5 3B.3 3 C.6 D.3 6第 Ⅱ 卷( 非选择题 共 90 分)本卷包括必考题和选考题两部分,第 13 ~ 21 题为必考题,每个试题考生都必须作答,第 22、23 题为选考题,考生根据要求作答.二、填空题:共 4 小题,每小题 5 分,共 20 分. 将答案填在答题卡上. 抛物线上的点 到 的距离为 的坐标为 l P数学二诊( 理工农医类)第3页( 共4 页)ab13. 随着国力的发展,人们的生活水平越来越好,我国的人均身高较新中国成立初期有大 幅提高. 为了掌握学生的体质与健康现状,合理制定学校体育卫生工作发展规划,某市进行了一次全市高中男生身高统计调查,数据显示全市30000 名高中男生的身高 ξ( 单位:cm) 服从正态分布 N (172,σ2 ),且 P (172 < ξ ≤ 180) = 0. 4,那么该市身高高于 180cm 的高中男生人数大约为 .14. 春节期间新型冠状病毒肺炎疫情在湖北爆发,为了打赢疫情防控阻击战,我省某医院 选派2 名医生,6 名护士到湖北A 、B 两地参加疫情防控工作,每地一名医生,3 名护士,其中甲乙两名护士不到同一地,共有种选派方法.15. 已知 a 、b 为正实数,直线 x + y + 1 = 0 截圆( x - a ) 2 + ( y - b ) 2 = 4 所得的弦长为 2 2 ,则a + 1的最小值为 . 16. 在△ABC 中,B 、C 的坐标分别为( - 2 2 ,0),(2 2 ,0),且满足sin B - sin C = 2sin A ,O→ → 2为坐标原点,若点 P 的坐标为(4,0),则A O ·A P 的取值范围为 .三、解答题:解答应写出文字说明、证明过程或演算步骤.17. ( 本题满分 12 分)已知数列{ a n } 满足:21 ·a 1 + 22 ·a 2 + 23 ·a 3 + … + 2n ·a n = ( n - 1)·2n +1 +2 对一切n ∈ N ∗ 成立.(1) 求数列{ a n } 的通项公式;(2) 求数列{a1n ·a n + 2} 的前 n 项和 S n.18. ( 本题满分 12 分)如图,四棱锥 P - ABCD 的底面 ABCD 中,△ABD 为等边三角形,△BCD 是等腰三角形,且顶角 ∠BCD = 120°,PC ⊥ BD , 平面 PBD ⊥ 平面 ABCD ,M 为 PA 中点.(1) 求证:DM ∥ 平面 PBC ;(2) 若 PD ⊥ PB ,求二面角 C - PA - B 的余弦值大小.19. ( 本题满分 12 分)贫困人口全面脱贫是全面建成小康社会的标志性指标. 党的十九届四中全会提出“ 坚决打赢脱贫攻坚战,建立解决相对贫困的长效机制” 对当前和下一个阶段的扶贫工作进行了前瞻性的部署,即 2020 年要通过精准扶贫全面消除绝对贫困,实现全面建成小康社会的奋斗目标. 为了响应党的号召,某市对口某贫困乡镇开展扶贫工作. 对某种农产品加工生产销售进行指导,经调查知,在一个销售季度内,每售出一吨该产品获利5 万元,未售出的商品,每吨亏损2 万元. 经统计 A ,B 两市场以往 100 个销售周期该产品的市场需求量的频数分布如下表: A 市场:B 市场:需求量( 吨) 90 100 110频数205030需求量( 吨) 90 100 110频数106030x2535把市场需求量的频率视为需求量的概率,设该厂在下个销售周期内生产n 吨该产品,在A、B 两市场同时销售,以X(单位:吨) 表示下一个销售周期两市场的需求量,Y(单位:万元) 表示下一个销售周期两市场的销售总利润.(1)求X >200 的概率;(2)以销售利润的期望为决策依据,确定下个销售周期内生产量n = 190 吨还是n = 200 吨? 并说明理由.20.(本题满分12 分)已知椭圆C:a2+y2b2= 1( a > b > 0) 的离心率为5 ,右焦点为抛物线y2= 4x 的焦点F.(1)求椭圆C 的标准方程;(2)O 为坐标原点,过O 作两条射线,分别交椭圆于M、N 两点,若OM、ON 斜率之积为-4求证:△MON 的面积为定值.21.(本题满分12 分)已知函数f( x) = e ax- x( a ∈ R,e 为自然对数的底数),g( x) = ln x + mx + 1.(1)若f(x) 有两个零点,求实数a 的取值范围;(2)当a = 1 时,x[f(x) + x] ≥g(x) 对任意的x ∈ (0, + ∞) 恒成立,求实数m 的取值范围.请考生在22、23 二题中任选一题作答. 注意:只能做所选定的题目. 如果多做,则按所做第一个题目计分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑.22.[选修4 - 4:坐标系与参数方程]( 本题满分10 分)已知点A 为圆C:( x - 1)2 + y2= 1 上的动点,O 为坐标原点,过P(0,4) 作直线OA 的垂线(当A、O 重合时,直线OA 约定为y 轴),垂足为M,以O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求点M 的轨迹的极坐标方程;(2)直线l 的极坐标方程为ρs i n(θ+π)=4,连接O A并延长交l 于B,求23.[选修4 - 5:不等式选讲]( 本题满分10 分)已知函数f(x) = x + 1 .(1)求不等式f( x) ≤4 - 2x - 3 的解集;(2)若正数m、n 满足m + 2n = mn,求证:f( m) + f( - 2n) ≥8.的最大值. OAOB,数学二诊( 理工农医类)第4页( 共4 页)高2017级数学( 理工农医类) 答案第1页( 共8 页)n (n · n n 2) 2 德阳市高中 2017 级“ 二诊” 试题数学参考答案与评分标准( 理工农医类)一、选择题( 每小题 5 分,共 60 分)二、填空题( 每小题 5 分,共 20 分)13. 3000 14. 24 15. 3 + 2 2 16. (12, + ∞ ) .三、解答题17. 解:(1) ∵ 21 ·a 1 + 22 ·a 2 + 23 ·a 3 + … + 2n ·a n = ( n - 1)·2n+ 1+ 2 ①∴ 当 n = 1 时,21 ·a 1 = 2∴ a 1 = 1 ................................................................................. 2 分 当 n ≥ 2 时,21·a 1 + 22·a 2 + 23·a 3 + … + 2n -1·a n -1 = ( n - 2)·2n + 2②① - ② 得:2n ·a n = n ·2n ∴ a n = n适合 a 1 = 1,故 a n = n ........................................................................................... 6 分 (2) a 1a +2= n ( 1+ = 1 ( 1n - n +1 2 )…………………………………… 8 分∴ S = 1 ⎡⎢ 1 - 1 ) + ( 1 - 1 ) + (1 - 1 ) + … + (1 - +1 )⎤⎥2 ⎢⎣ 13 24 35 n 2 ⎥⎦ = 1 (1 +1 -n +1 - +1 )2 2 1 n 2= n (3n + 5). 4( n + 1)( n + 2)………………………………………………… 12 分18. (1) 证明:设 AB 中点为 N ,连接 MN 、DN∵ △ABD 为等边三角形 ∴ DN ⊥ AB∵ DC = CB ,∠DCB = 120°n高2017级数学( 理工农医类) 答案第2页( 共8 页)2∴ ∠CBD = 30°∴ ∠ABC = 60° + 30° = 90° 即 CB ⊥ AB ∵ DN ⊥ AB∴ DN ∥ BC∵ BC ⊂ 平面 PBC ,DN ⊄ 平面 PBC∴ DN ∥ 平面 PBC .................................................................................... 2 分 ∵ MN 为 △PAB 的中位线 ∴ MN ∥ PB∵ PB ⊂ 平面 PBC ,MN ⊄ 平面 PBC∴ MN ∥ 平面 PBC .................................................................................... 4 分 ∵ MN 、DN 为平面 DMN 内二相交直线 ∴ 平面 DMN ∥ 平面 PBC ∵ DM ⊂ 平面 DMN∴ DM ∥ 平面 PBC ................................................................................... 6 分(2) 解:设 BD 中点为 O ,连接 AO 、CO∵ △ABD 为等边三角形,△BCD 是等腰三角形,且顶角 ∠BCD = 120° ∴ AO ⊥ BD ,CO ⊥ BD∴ A 、C 、O 共线∵ PC ⊥ BD ,BD ⊥ CO ,PC ∩ CO = C ,PC ,CO ⊂ 平面 PCO∴ BD ⊥ 平面 PCO ........................................................................................ 7 分 ∵ PO ⊂ 平面 PCO∴ BD ⊥ PO∵ 平面 PBD ⊥ 平面 ABCD ,交线为 BD ,PO ⊂ 平面 PBD∴ PO ⊥ 平面 ABCD ...................................................................................... 8 分 设 AB = 2,则 AO = 3在 △B CD 中,由余弦定理,得:B D 2 = B C 2 + CD 2 - 2B C ·CD ·c o s ∠B CD 又 ∵ B C = CD∴ 22 = 2B C 2 - 2B C 2 ·c o s 120°∴ CB = CD,CO 33∵ PD ⊥ PB ,O 为 BD 中点 ∴ PO =1BD = 1高2017级数学( 理工农医类) 答案第3页( 共8 页)→n · O →B→n ·O →B 3→n ·B →A = 0⇒ 7建立直角坐标系 O - xyz ( 如图), 则 C (-3,0,0 ),P (0,0,1),A ( 3 ,0,0), B (0,1,0) ................................. 9 分 ∴ B →A = ( 3 , - 1,0),P →A = ( 3 ,0, - 1) 设平面 P AB 的法向量为→n = ( x ,y ,z ),则{→n ·P →A = 0{3 x - y = 03 x - z = 0 取 x = 1, 则 y = z = 3∴ →n = (1, 3 , 3 ) ………………………………………………………… 10 分 平面 P A C 的法向量为O →B = (0,1,0)c osn ,O →B > ==21 7………………………………… 11 分∵ 二面角 C - PA - B 为锐角 ∴ 二面角 C - PA - B 的余弦值大小为 21. ……………………………12 分 19. 解:(1) 设“ A 市场需求量为90,100,110 吨” 分别记为事件 A 1 ,A 2 ,A 3 ,“ B 市场需求量为 90,100,110 吨” 分别记为事件 B 1 ,B 2 ,B 3 ,则P ( A 1 ) = 0. 2,P ( A 2 ) = 0. 5,P ( A 3 ) = 0. 3P ( B 1 ) = 0. 1,P ( B 2 ) = 0. 6,P ( B 3 ) = 0. 3. P ( X > 200) = P ( A 2 B 3 + A 3 B 2 + A 3 B 3 )………………………………… 2 分 = P ( A 2 ) P ( B 3 ) + P ( A 3 ) P ( B 2 ) + P ( A 3 ) P ( B 3 )= 0. 5 × 0. 3 + 0. 3 × 0. 6 + 0. 3 × 0. 3 = 0. 42 ................... 5 分(2) X 可取 180,190,200,210,220P ( X = 180) = P ( A 1 B 1 ) = 0. 2 × 0. 1 = 0. 02 ..................................... 6 分 P ( X = 190) = P ( A 2 B 1 + A 1 B 2 ) = 0. 5 × 0. 1 + 0. 2 × 0. 6 = 0. 17 ……… 7 分 当 n = 190 时,E (Y ) = (180 × 5 - 10 × 2) × 0. 02 + 190 × 5 × (1 - 0. 02) = 948. 6…………………………………………………………………………… 9 分 当 n = 200 时,E ( Y ) = (180 × 5 - 20 × 2) × 0. 02 + (190 × 5 - 10 × 2) ×高2017级数学( 理工农医类) 答案第4页( 共8 页)= t ( - 5 5 - t 25 - 2 5 - t 2 5 555 4 + 5 2k 4 0. 17 + 200 × 5 × (1 - 0. 02 - 0. 17) = 985. 3 ∵ 948. 6 < 985. 3………………………… 11 分 ∴ n = 200 时,平均利润大,所以下个销售周期内生产量 n = 200 吨. 20. 解:(1) 抛物线 y 2 = 4x 的焦点为 F (1,0)∴ c = 1 … 12 分∵ e = 5ca 5∴ a = 5 ,b = 2 ∴ 椭圆方程为x2+ y 24= 1 ........................................................... 3 分(2) 当 MN 与 x 轴垂直时,设直线 MN 的方程为:x< t < 5 ,t ≠ 0)x 2 代入 5 + y 24= 1 得:M (t ,2 5 - t 2 ) ,N (t , - 2 )∴ k ·k = 5 - t 2 5 ·= - 4 ·5 - t 21 2t t 5 t 2∴ - 4 ·5 - t 2 = - 4解得:t 2 = 55 ∴ S △MON t2= 125 t ·42 = 5 ............................................ 4 分 当 MN 与 x 轴不垂直时,设 M ( x 1 ,y 1 ),N ( x 2 ,y 2 ),MN 的方程为 y = kx + m ⎧⎪y = kx + m⎪由⎨x 2 ⎪⎩ 5 y 2 = 1 ⇒(4 + 5k 2 ) x 2 + 10kmx + 5m 2 - 20 = 0 …………… 5 分由 △ > 0⇒5k 2 + 4 > m 2 .......... ① x 1 + x 2 = - 10km4 + 5k 2 ,x 1 ·x 2 =5m 2 - 20 ........................................ 6 分∵ k ·k= - 4∴ y 1 ·y 2 = - 4∴ 5y y + 4x x = 0 …… 7 分OMON5x 1 x 2 51 21 2即(5k 2 + 4) x 1 ·x 2 + 5mk ( x 1 + x 2 ) + 5m 2 = 05 - t 25 ∴ 2 +高2017级数学( 理工农医类) 答案第5页( 共8 页)5k 2 + 4 - m 2 2m 2 - m 2 ) 4 + 52k ∴=S △x∴ (5k 2+ 4)·5m 2- 20+ 5mk · ( - 10km )+ 5m 2 = 0 4 + 5k 2 整理得:2m 2 = 5k 2 + 4 代入 ① 得:m ≠ 04 + 5k 2………………………………………………… 9 分 M N = 1 + k 2 ( x 1 + x 2 ) 2- 4x 1 ·x 2= 1 + k 2= 4 5 1 + k25k 2 + 4 - m 2 ……………………………… 10 分O 到 MN 的距离 d =m1 + k 2………………………………………… 11 分1MON2MN d = 2 5 = 2 5 = 5m 4 + 5k 2 m 2m 2综上:S △MON = 5 为定值. ………………………………………………21. 解:(1) f ( x ) 有两个零点 ⇔ 关于 x 的方程 e ax = x 有两个相异实根由 e ax > 0,知 x > 012 分∴ f ( x ) 有两个零点 ⇔ a =ln x有两个相异实根. 令 G ( x ) = ln x ,则 G′( x ) = 1 - ln x………………………… 1 分 xx 2由 G′( x ) > 0 得:0 < x < e ,由 G′( x ) < 0 得:x > e ∴ G ( x ) 在(0,e ) 单调递增,在( e , + ∞ ) 单调递减 ∴ G ( x ) ma x = G ( e ) = 1e .........................................................................................2 分又 ∵ G (1) = 0∴ 当 0 < x < 1 时,G ( x ) < 0,当 x > 1 时,G ( x ) > 0高2017级数学( 理工农医类) 答案第6页( 共8 页)e 0x x 当 x → + ∞ 时,G ( x ) → 0 ............................................................ 3 分 ∴ f ( x ) 有两个零点时,实数 a 的取值范围为(0,1e ) ...............4 分 (2) 当 a = 1 时,f ( x ) = e x - x∴ 原命题等价于 xe x ≥ ln x + mx + 1 对一切 x ∈ (0, + ∞ ) 恒成立⇔m ≤ e x - ln x - 1对一切 x ∈ (0, + ∞ ) 恒成立 ................. 5 分令 F ( x ) = e x - ln x - 1( x > 0) ∴ m ≤ F ( x ) minxxF′( x ) = e x+ ln x = x 2 e x + ln x x 2 x 2令 h ( x ) = x 2 e x + ln x ,x ∈ (0, + ∞ ),则 h ′( x ) = 2x e x + x 2 e x +1x> 0 ∴ h ( x ) 在(0, + ∞ ) 上单增又 h (1) = e > 0,h ( 1)= e 1e - 2 - 1 < e 0 - 1 = 0∴ ∃x 0 ∈( 1e ,1 ) ,使 h ( x 0) = 0 即 x 2 ex 0+ l n x 0 = 0①当 x ∈ (0,x 0 ) 时,h ( x ) < 0,当 x ∈ ( x 0 , + ∞ ) 时,h ( x ) > 0即 F ( x ) 在(0,x 0 ) 递减,在( x 0 , + ∞ ) 递增………… 7 分∴ F ( x ) m in = F (x 0 ) = e x 0 - ln x 0 - 1 ……………………………………… 8 分 x 0 x 0 由 ① 知 x 2 e x 0 = - ln x∴ x e x 0 = -ln x 0= 1 ln 1= (l n 1 )e l n x10 0 0x 0 xx 0∵ 函数 φ( x ) = xe x 在(0, + ∞ ) 单调递增 ∴ x 0 = ln x 1即 x 0 = - ln x 0 ………………………………………………… 10 分∴ F ( x ) = e -l n x 0 - - x 0 - 1 = 1 + 1 - 1= 1 ……………………… 11 分min ∴ m ≤ 1x 0 x 0 x 0 x 0∴ 实数 m 的取值范围为( - ∞ ,1] .............................................. 12 分x高2017级数学( 理工农医类) 答案第7页 ( 共8 页)OA OB{4 -π3822. 解:(1) 设 M 的极坐标为( ρ,θ),在 △OPM 中,有 ρ = 4sin θ∴ 点 M 的轨迹的极坐标方程为 ρ = 4sin θ ..................................................... 4 分(2) 设射线 OA :θ = α,α ∈ (- π , π),圆 C 的极坐标方程为 ρ = 2cos θ2 由ρ = 2cos θ得 OA = ρ θ = α 1⎧⎪ρs i n (θ + π )= 42= 2cos α ............................................................. 5 分由⎪ 3 得: OB = ρ2 =……………………… 6 分 ⎪⎩θ = α ∴=2cos α s i n (α + 3 )4s i n (α + π= 1 c o s α·s i n (α +π )2= 1 c o s α (s i n αc o s π3 + cos αsin π )2 3 3= 1 sin αcos α2 α 4 4 = 1 sin2αα + 1)8 8= 1 s i n (2α + π)+………………………………………… 8 分4 3 8∵ α ∈ (- π , π ) ∴ -2π< 2α + π < 4π2 23 33∴ 当 2α + π = π ,即 α = π时,=9 分3212 OBmax8∴ 的最大值为2 + 3. . ………………………………………… 10 分23. 解:(1) f ( x ) ≤ 4 - 2x - 3 等价于 {x < - 1或OA OB) ⎨高2017级数学( 理工农医类) 答案第8页 ( 共8 页)⎨⎪ ⎪x 3 ⎪ 2⎪ 2 n = 22 ⎧⎪- 1 ≤ x ≤3 ⎧⎪- 1 ≤ x ≤ 3⎧⎪x > 3 ⎪ 2 或 ⎨ 2 ⎪⎩( x + 1) - (2x - 3) ≤ 4 ⎧⎪x < - 1 ⎪⎩( x + 1) + (2x - 3) ≤ 4 由 得:⎨ ⎩≥ - 2 ⇒x ∈ Ø由 得:⎨⎪⎩x ≥ 0 ⎧⎪x > 3 2 ⇒0 ≤ x ≤ 3 由 得:⎨2 ⇒3 < x ≤ 2 ⎪⎩x ≤ 2∴ 原不等式的解集为{x 0 ≤ x ≤ 2} .......................................... 5 分 (2) ∵ m > 0,n > 0,m + 2n = mn∴ m + 2n = 1 ( m ·2n ) ≤ 1×( m + 2n ) 22 2 4∴ m + 2n ≥ 8 .......................................................................... 7 分 m = 2n m + 2n = mn,即{m = 4时取等号∴ f ( m ) + f ( - 2n ) = m + 1 + - 2n + 1 ≥ m + 2n≥ 8 ……… 9 分当且仅当 - 2n + 1 ≤ 0 即 n ≥ 1时取等号∴ f ( m ) + f ( - 2n ) ≥ 8.…………………………………………………10 分⎪ 当且仅当{。

德阳市高中2017级第三次诊断考试物理试题参考答案14.A 15.B 16.D 17.C 18.D 19.AC 20.BD 21.BD22.(6分)(1)222d xt (2分)(2)①D(2分) ② AB(2分) 23.(9分)(1)D(2分) F(2分)(2) ①将滑动触头移至最左端(各2分) (3)12(1)r k R =-(3分)24．(12分)解：(1)离子在加速电场中加速的过程中,由动能定理有： 2102qU mv =-(2分)离子在静电分析器中做匀速圆周运动,根据牛顿第二定律有： 2v qE m R =(2分)解得： 2ER U =(2分)(2)离子在磁分析器中做匀速圆周运动,由牛顿第二定律有： 2v qvB m r =(3分)(1分) (2分)25.(20分)解：(1)AB 一起向右匀减速μ1(m +3m )g =4ma 1 (2分)由S =v 0t 1+12t 12 (2分) 得μ1=0.1 (2分)(2)木板B 与物块C 碰前速度v 1=v 0-a 1t 1解得：14/v m s = (2分) 依题意可知,B 与C 碰的过程遵从动量守恒,则有：3mv 1=3mv '1+6mv '2 (2分)因为 v '1=−43m /s 解得：v '2=83m /s (2分)(3)B 与C 碰后对A,由牛顿第二定律得：μ2m g =ma 2 式中μ2=0.4为A 与B 间的动摩擦因数,a 2为A 的加速度大小 解得：a 2=4m /s 2 (1分) 对B,由牛顿第二定律得：μ2mg +μ1(m +3m )g =3ma 3 式中a 3为B 向左做匀减速运动的加速度大小 解得：a 3=83m /s 2(1分) A 向右减速至0 m/s,用时t 2=v 1a 2=1s ,B 向左减速至0 m/s,用时t 3=−v '1a 3=0.5s t 2＞t 3，且μ2mg −μ1(m +3m )g =0可知,B 先停止运动,直至A 停下 (2分) 设x 2为A 向右减速运动的位移,x 3为B 向左减速运动的位移x 2=v 122a 2=2m ,x 3=v '2❑12a 3=13m (2分)则木板的最小长度l m =x 2+x 3=73m (2分) 选作题3--4(15分)34.(1) BCE(2)解.①设入射角为i ,折射角为r由光路图可知, tan i =d h =√33(1分) i +r =90o 60o r (1分) n =sin rsin i (1分) n =√3 (2分) ②光从液体到空气在C 点恰发生全反射,临界角为C sin c =1n (1分)而AC 长度R =h ta n c (1分)照亮区域的面积S =π(R 2−d 2)(1分)解得 S =4.71m 2(2分)。

德阳市高中2017级第二学年统考化学试卷2019.07.02德阳市高二下学期化学期末考试试题说明：1.本试卷分第Ⅰ卷和第Ⅱ卷，共6页。

考生作答时，须将答案答在答题卡上，在本试卷或草稿纸上答题无效。

考试结束后，将答题卡交回。

2.本试卷满分100分，90分钟完卷。

可能用到的相对原子质量：H－1 B－11 C－12 N－14 0－16 Mg－24 Fe－56第Ⅰ卷(选择题共42分)一、选择题(本题包括14小题，每小题3分，共42分。

每小题只有一个．．．．选项符合题意)1.化学与人类生产、生活、科研密切相关，下列有关说法错误的是A.次氯酸钙可用于生活用水的消毒B.在糕点包装袋内放置活性碳粉作抗氧化剂C.棉袜子的主要成分属于有机高分子化合物D.电动汽车的使用有助于减少氮氧化物的排放2.下列有关化学用语表示正确的是A.CH4的比例模型：B.Fe2＋的价电子排布式：3d54s1C.甲酸乙酯的结构简式：CH3OOCCH3D.Na2CO3水解的离子方程式：CO32－＋2H2O H2CO3＋2OH－3.常温时，能证明乙酸是弱酸的实验事实是A.CH3COOH溶液与Fe反应放出H2B.0.1mol/L CH3COOH溶液的pH大于1C.CH3COOH溶液与NaHCO3反应生成CO2D.0.1mol/L CH3COOH溶液可使紫色石蕊变红4.下列说法中正确的是A.淀粉、蛋白质和油脂都是天然高分子化合物B.花生油、菜籽油、芝麻油水解产物完全不同C.乙酸可与乙醇、钠、新制Cu(OH)2悬浊液等物质反应D.某些蛋白质可溶于溶剂形成胶体，但遇CuSO4溶液发生盐析5.有机物命名正确的是A.1，3－二甲基丁烷B.2，3，5－三甲基己烷C.2，3－二甲基－2－乙基己烷D.2，3－二甲基－4－乙基戊烷6.已知有机物a：，有机物b：，下列说法中正确的是A.a是苯的同分异构体B.b的一氯代物有5种C.a中6个碳原子都在同一平面内D.b可使溴水、酸性KMnO4溶液褪色，且反应类型相同7.下列叙述正确的是A.Na、Mg、Al原子的第一电离能逐渐减小B.N原子的轨道表示式：C.NO3－中的化学键有σ键和π键D.离子晶体中每个离子周围均吸引着6个带相反电荷的离子8.NA是阿伏加德罗常数的值。

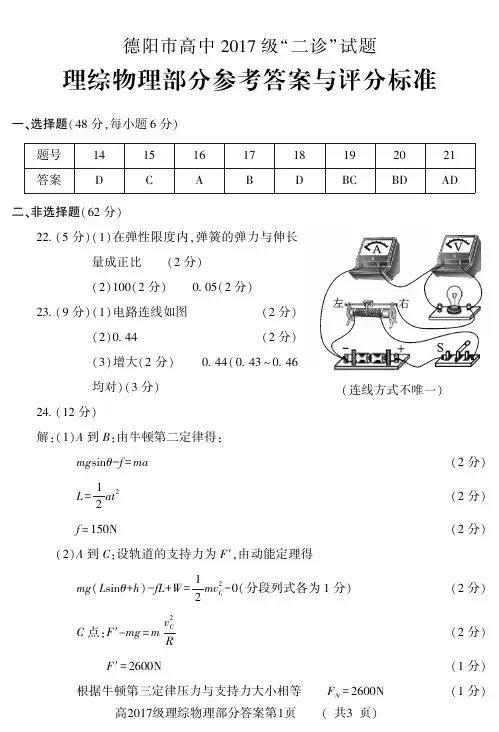
x德阳市高中2017级“二诊”考试理综物理部分二、选择题(本题共8小题，每小题6分。

在每小题给出的四个选项中，14--18题只有一项符合题目要求，19--21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分)14.太阳内部持续不断地发生着4个质子（11H ）聚变为1个氦核（24He ）的热核反应, 核反应方程是411H →24He +2X ，这个核反应释放出大量核能。

已知质子、氦核、X 的质量分别为m 1、m 2、m 3，真空中的光速为c 。

下列说法中正确的是（ ）A ．方程中的X 表示中子01nB ．方程中的X 表示电子−10eC ．这个核反应中质量亏损Δm=m 1－m 2－m 3D ．这个核反应中释放的核能ΔE =(4m 1－m 2－2m 3)c 215．甲、乙两车某时刻由同一地点、沿同一方向开始做直线运动。

甲、乙两车的位置x 随时间t 的变化如图所示，则（ ） A ．0时刻，甲车速度比乙车小 B ．t 2时刻，甲乙两车速度相等C ．0～t 1时间内，甲车的平均速度比乙车大D ．0～t 2时间内，甲车通过的距离大16.两行星 A 和 B 各有一颗卫星 a 和 b ，卫星的圆轨道接近各自的行星表面，如果两行星质量之比 M A :M B =2:1，两行星半径之比 R A :R B =1:2，则两个卫星周期之比 T a :T b 为 （ ）A. 1:4B. 4:1C. 1:2D. 2:117.如图所示，两根相距为L 的平行直导轨水平放置，R 为固定电阻，导轨电阻不计。

电阻阻值也为R 的金属杆MN 垂直于导轨放置，杆与导轨之间有摩擦，整个装置处在竖直向下的匀强磁场中，磁感应强度大小为B 。

t=0时刻对金属杆施加一水平外力F 作用，使金属杆从静止开始做匀加速直线运动。

下列关于通过R 的电流I （图A 为抛物线）、杆与导轨间的摩擦生热Q （图B 为抛物线）、外力F 、外力F 的功率P 随时间t 变化的图像中正确的是（ ）18.如图所示，物体A 、B 的质量分别为m 、2m ，物体B 置于水平面上，B 物体上部半圆型槽的半径为R ，将物体A 从圆槽的右侧最顶端由静止释放，一切摩擦均不计。

德阳市高中2017级”二诊”考试英语试卷注意事项:1. 本试卷分第I卷(选择题)和第II卷(非选择题)两部分，全卷150分，考试时间120分钟。

2. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上指定的位置。

3. 全部答案在答题卡上完成，答在本试卷上无效。

考试结束后，将答题卡交回。

第 I 卷(选择题共100分)第一部分:听力(共两节，满分30分)做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节(共5小题；每小题1. 5分，满分7. 5分)听下面5段对话，每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒种的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.【此处可播放相关音频，请去附件查看】What is the man doing?A. Reading a story.B. Watching a new film.C. Writing a detective story.【答案】A【解析】【原文】W: Oh, I see you’re in the middle of that new detective story. Is it any good?M: I can’t put it down.2.【此处可播放相关音频，请去附件查看】What is the man’s suggestion?A. Buying a new refrigerator.B. Putting the refrigerator far away.C. Having the refrigerator fixed.【答案】C【解析】【原文】M: I’m no expert. But that noise in your refrigerator doesn’t sound good.Maybe you should call and have it checked out.W: You are right. And I suppose I’ve put it off long enough.3.【此处可播放相关音频，请去附件查看】What does the man hope to do?A. Attend a meeting.B. Watch a basketball match.C. Rest for a couple of hours.【答案】A【解析】【原文】W: Take the medicine and I’m sure you’ll get well again in a couple of hours. M: I hope so. Or I won’t be able to take part in the meeting about tomorrow’s basketball match.4.【此处可播放相关音频，请去附件查看】What kind of music does the woman like best?A. Folk music.B. Pop music.C. Classical music. 【答案】C【解析】【原文】M: I enjoyed all kinds of music. What music do you like?W: Folk music had appealed to me very much before I came to have a passion for pop music, but now I think nothing can compare with classical music.5.【此处可播放相关音频，请去附件查看】How does the woman feel?A. Excited.B. Indifferent.C. Disappointed. 【答案】C【解析】【原文】M: Honey, I’m home.W: Did you remember to buy the tickets? M: Well, I remembered,but they were sold out. W: Oh no. I was really looking forward to the play. 第二节(共15小题；每小题1. 5分，满分22. 5分)听下面5段对话或独白。

2020届四川省德阳市高三“二诊”考试数学（文）试题一、单选题 1．已知复数21z i =+　，其中i 为虚数单位，则z =（ ）A ．BC ．2D【答案】D【解析】把已知等式变形，然后利用数代数形式的乘除运算化简，再由复数模的公式计算得答案. 【详解】 解：()()()2121111i z i i i i -===-++- ，则z =. 故选：D. 【点睛】本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题.2．函数y =A ，集合(){}2log 11B x x =+>，则A B =（ ）A ．{}12x x <≤ B ．{}22x x -≤≤C ．{}23x x -<<D ．{}13x x <<【答案】A【解析】根据函数定义域得集合A ，解对数不等式得到集合B ，然后直接利用交集运算求解. 【详解】解：由函数y =240x -≥，解得22x -≤≤，即{}22A x x =-≤≤；又()22log 11og 2l x +>=，解得1x >，即{}1B x x =>， 则{}12A B x x ⋂=<≤. 故选：A. 【点睛】本题考查了交集及其运算，考查了函数定义域的求法，是基础题.3．执行如图所示的程序框图，若输出的结果为3，则可输入的实数x 值的个数为（ ）A ．1B ．2C ．3D ．4【答案】C【解析】试题分析：根据题意，当2x ≤时，令213x -=，得2x =±；当2x >时，令2log 3x =，得9x =，故输入的实数值的个数为3．【考点】程序框图． 4．函数()()cos ln x x x xf x e e -=+在[],ππ-的图象大致为（ ）A ．B ．C ．D ．【答案】A【解析】根据函数的奇偶性，在x π=时函数范围的判断进行排除，即可得答案. 【详解】解：由已知()()()()()cos cos ln ln x x x xx x x xf x f x e e e e -----==-=-++，则函数()()cos ln x x x xf x e e -=+在[],ππ-上是奇函数，故排除B ；又()()()()cos 0,1ln ln ln ln f e e e e e e e πππππππππππππ---==-<->-=-+++，故排除CD ； 故选：A. 【点睛】本题考查函数图像的识别，利用函数的性质，如奇偶性，单调性，特殊点的函数值等进行排除是常用的方法，是基础题. 5．要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin 2y x =的图象（ ） A ．向右平移6π个单位 B ．向右平移3π个单位 C ．向左平移3π个单位 D ．向左平移6π个单位 【答案】D【解析】直接根据三角函数的图象平移规则得出正确的结论即可； 【详解】解：函数sin 2sin 236y x x ππ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， ∴要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin 2y x =的图象向左平移6π个单位． 故选：D ． 【点睛】本题考查三角函数图象平移的应用问题，属于基础题．6．二项式52x ⎫-⎪⎭的展开式中，常数项为（ ）A ．80-B ．80C ．160-D ．160【答案】A【解析】求出二项式52x ⎫⎪⎭的展开式的通式，再令x 的次数为零，可得结果.【详解】解：二项式52x ⎫⎪⎭展开式的通式为()()55225215512rrr rrr r rr T C x C x---+-+=-=-，令5202rr --+=，解得1r =， 则常数项为()11451280C -=-.故选：A. 【点睛】本题考查二项式定理指定项的求解，关键是熟练应用二项展开式的通式，是基础题. 7．已知122a -=，1313b ⎛⎫= ⎪⎝⎭，121log 5c =，则（ ） A ．b a c << B ．a b c <<C ．c b a <<D ．b c a <<【答案】A【解析】先分析,,a b c 与1的大小关系,可得0,1a b c <<<,再分析66,a b 的大小即可.【详解】 因为102221a -=<=,10311133b <⎛⎫⎛⎫= ⎪ ⎪⎝⎝⎭=⎭,12221log log 5log 215c ==>=.故c 最大. 又166321228a -⨯-===,16236111339b ⨯⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,故66a b >,又,0a b >故a b >. 故b a c <<. 故选：A 【点睛】本题主要考查了根据指对幂函数的单调性与计算分析函数值大小的问题.属于基础题. 8．已知l 为抛物线24x y =的准线，抛物线上的点M 到l 的距离为d ，点P 的坐标为()4,1，则MP d +的最小值是（ ）A．B ．4C ．2D．1【答案】B【解析】设抛物线焦点为F ，由题意利用抛物线的定义可得，当,,P M F 共线时，MP d +取得最小值，由此求得答案.【详解】解：抛物线焦点()0,1F ，准线1y =-， 过M 作MN l ⊥交l 于点N ，连接FM由抛物线定义MN MF d ==，244MP d MP MF PF ∴+=+≥==，当且仅当,,P M F 三点共线时，取“＝”号， ∴MP d +的最小值为4. 故选：B. 【点睛】本题主要考查抛物线的定义、标准方程，以及简单性质的应用，体现了数形结合的数学思想，属于中档题.9．不等式组201230x y y x x y -≥⎧⎪⎪≥⎨⎪+-≤⎪⎩表示的平面区域为Ω，则（ ）A ．(),x y ∀∈Ω，23x y +>B ．(),x y ∃∈Ω，25x y +>C ．(),x y ∀∈Ω，231y x +>- D ．(),x y ∃∈Ω，251y x +>- 【答案】D【解析】根据题意，分析不等式组的几何意义，可得其表示的平面区域，设1222,1y z x y z x +=+=-，分析12,z z 的几何意义，可得12,z z 的最小值，据此分析选项即可得答案. 【详解】解：根据题意，不等式组201230x y y x x y -≥⎧⎪⎪≥⎨⎪+-≤⎪⎩其表示的平面区域如图所示，其中()2,1A ，()1,2B ， 设12z x y =+，则122z x y =-+，1z 的几何意义为直线122zx y =-+在y 轴上的截距的2倍，由图可得：当122z x y =-+过点()1,2B 时，直线12z x y =+在y 轴上的截距最大，即25x y +≤，当122z x y =-+过点原点时，直线12z x y =+在y 轴上的截距最小，即20x y +≥， 故AB 错误； 设221y z x +=-，则2z 的几何意义为点(),x y 与点()1,2-连线的斜率， 由图可得2z 最大可到无穷大，最小可到无穷小，故C 错误，D 正确； 故选：D. 【点睛】本题考查本题考查二元一次不等式的性质以及应用，关键是对目标函数几何意义的认识，属于基础题.10．平行四边形ABCD 中，已知4AB =，3AD =，点E 、F 分别满足2AE ED =，DF FC =，且6AF BE ⋅=-，则向量AD 在AB 上的投影为（ ）A ．2B ．2-C ．32D ．32-【答案】C【解析】将,AF BE 用向量AD 和AB 表示，代入6AF BE ⋅=-可求出6AD AB ⋅=，再利用投影公式AD AB AB⋅可得答案.【详解】解：()()AF BE AD DF BA AE ⋅=+⋅+21123223AD AB AD AD AB AB AB AD =⋅+⋅-⋅+⋅22421346332AD AB =⋅+⨯-⨯=， 得6AD AB ⋅=，则向量AD 在AB 上的投影为6342AD AB AB⋅==. 故选：C. 【点睛】本题考查向量的几何意义，考查向量的线性运算，将,AF BE 用向量AD 和AB 表示是关键，是基础题.11．已知ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，且60A =︒，3b =，AD 为BC 边上的中线，若72AD =，则ABC 的面积为（ ）A ．BC ．154D 【答案】B【解析】延长AD 到E ，使AD DE =，连接,BE CE ，则四边形ABEC 为平行四边形，根据余弦定理可求出5AB =，进而可得ABC 的面积. 【详解】解：延长AD 到E ，使AD DE =，连接,BE CE ，则四边形ABEC 为平行四边形， 则3BE AC ==，18060120ABE ∠=-=，27AE AD ==， 在ABE △中，2222cos AE AB BE AB BE ABE =+-⋅∠ 则2227323cos120AB AB =+-⨯⨯⨯，得5AB =，11sin 60532224ABCSAB AC =⋅⋅=⨯⨯⨯=. 故选：B.【点睛】本题考查余弦定理的应用，考查三角形面积公式的应用，其中根据中线作出平行四边形是关键，是中档题.12．已知实数0a >，1a ≠，函数()2,14ln ,1x a x f x x a x x x ⎧<⎪=⎨++≥⎪⎩在R 上单调递增，则实数a 的取值范围是（ ） A ．12a <≤ B ．5a < C ．35a << D ．25a ≤≤【答案】D【解析】根据题意，对于函数分2段分析：当1,()xx f x a <=，由指数函数的性质分析可得1a >①，当241,()ln x f x x a x x≥=++，由导数与函数单调性的关系可得24()20af x x x x'=-+≥，在[1,)+∞上恒成立，变形可得2a ≥②，再结合函数的单调性，分析可得14a ≤+③，联立三个式子，分析可得答案. 【详解】解：根据题意，函数()2,14ln ,1x a x f x x a x x x ⎧<⎪=⎨++≥⎪⎩在R 上单调递增，当1,()xx f x a <=，若()f x 为增函数，则1a >①，当241,()ln x f x x a x x≥=++， 若()f x 为增函数，必有24()20af x x x x'=-+≥在[1,)+∞上恒成立， 变形可得：242a x x≥-， 又由1x ≥，可得()242g x x x =-在[1,)+∞上单调递减，则2442212x x -≤-=，若242a x x≥-在[1,)+∞上恒成立，则有2a ≥②， 若函数()f x 在R 上单调递增，左边一段函数的最大值不能大于右边一段函数的最小值，则需有145a ≤+=，③ 联立①②③可得：25a ≤≤. 故选：D. 【点睛】本题考查函数单调性的性质以及应用，注意分段函数单调性的性质.13．ABC 是边长为23的等边三角形，E 、F 分别为AB 、AC 的中点，//EF BC ，沿EF 把AEF 折起，使点A 翻折到点P 的位置，连接PB 、PC ，当四棱锥P BCFE -的外接球的表面积最小时，四棱锥P BCFE -的体积为（ ） A ．53B ．33C ．6 D ．36【答案】D【解析】由题意知当四棱锥P BCFE -的外接球的表面积最小时球半径最小.且球心O 到四棱锥P BCFE -各顶点的距离相等,再计算此时P 到平面BCFE 的距离求解即可. 【详解】由题,取BC 中点O ,连接,,EF EO FO ,因为ABC 是边长为23的等边三角形,故,,,AEF EBO EOC EFO 均为边长为3的等边三角形.连接AO 交EF 于G .易得G 为EF 中点,且,AO EF AO BC ⊥⊥.32AG OG ==.又四棱锥P BCFE -的外接球的表面积最小时球半径最小,且球心到,,,E F B C 的距离相等.故球心在过O 且与平面BCFE 垂直的直线上.故当球心为O 时,球半径取得最小值3.此时有33,2OP OG PG ===. 在POG 中由余弦定理可得2222333122cos 3322OGP ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭∠==⎛⎫⋅ ⎪⎝⎭. 因为,GO EF GP EF ⊥⊥,故EF ⊥平面OPG .故P 到平面BCFE 的距离231sin 1223d PG OGP ⎛⎫=⋅∠=-= ⎪⎝⎭又底面(113362332322BCFE S =⨯⨯=故选：D 【点睛】本题主要考查了几何体外接球的问题,需要根据题意分析球心的位置,并根据解三角形求解相关的线段长度进而求得体积等.需要一定的空间想象能力与计算能力.属于难题. 14．ABC 是边长为23E 、F 分别在AB 、AC 上滑动，EF BC ∥，沿EF 把AEF 折起，使点A 翻折到点P 的位置，连接PB 、PC ，则四棱锥P BCFE -的体积的最大值（ ） 为 A ．2 B 3C ．3D ．2【答案】D【解析】以四边形BCFE 为底面,易得当平面PBC 与平面BCFE 垂直时四棱锥P BCFE -的体积取最大值.再求得底面积与高即可.【详解】以四边形BCFE 为底面,则当P 与平面BCFE 距离最远时四棱锥P BCFE -的体积取最大值.易得此时平面PBC 与平面BCFE 垂直. 作AM BC ⊥于M ,交EF 于N .则易得AN EF ⊥,sin 3AM AC C =⋅=.又因为ABC 是边长为23的等边三角形, 设NF x =,则2EF x =,3AN x =.则33NM x =-.此时底面(())2122333332BCFE S x x x =+⨯=-. 故四棱锥P BCFE -的体积为)()22133333V x x x x =-=-.其中(3x ∈.设()()23f x x x =-,故()()()22'3233f x x x x x=-+⋅-=-,令()'0f x =有1x =.故()()23f x x x=-在()0,1上单调递增,在()1,3上单调递减.故()f x 的最大值为()()211312f =-=.故选：D 【点睛】本题主要考查了利用导数求解立体几何中体积的最值问题,需要根据题意分析取最值时的垂直情况,再设对应的自变量,列出关于体积的表达式,求导分析最值求解即可.属于中档题.二、填空题15．已知函数()2f x x ax =+的图象在点()()1,1A f 处的切线与直线l ：320x y -+=垂直，则实数a 的值为__________． 【答案】5-【解析】根据导数的几何意义求解()2f x x ax =+的图象在点()()1,1A f 处的切线斜率,再根据直线垂直列式求解即可. 【详解】由题, ()'2f x x a =+,故函数在点()()1,1A f 处的切线斜率为()'12f a =+. 又320x y -+=斜率为13,故()12153a a +=-⇒=-. 故答案为：5- 【点睛】本题主要考查了导数的几何意义,属于基础题.16．在一个袋子中装有分别标注1、2、3、4、5的5个小球，这些小球除标注的数字外完全相同，现从中随机取出2个小球，则取出的小球标注的数字之差的绝对值为2或4的概率是__________． 【答案】25【解析】利用枚举法将所有可能的情况列出再分析即可. 【详解】易得所有可能的情况有()()()()()()()()()()1,2,1,3,1,4,1,5,2,3,2,4,2,5,3,4,3,5,4,5共10种情况.其中满足取出的小球标注的数字之差的绝对值为2或4的有()()()()1,3,1,5,2,4,3,5 共4种情况.故概率取出的小球标注的数字之差的绝对值为2或4的概率是42105=. 故答案为：25【点睛】本题主要考查了枚举法求解古典概型的方法,属于基础题.17．已知a 、b 为正实数，直线10x y ++=截圆()()224x a y b -+-=所得的弦长为ab 的最大值为__________．【答案】14【解析】根据垂径定理求得,a b 的关系,【详解】因为直线10x y ++=截圆()()224x a y b -+-=所得的弦长为且圆的半径为2.故圆心(),a b 到直线的距离d ===,因为a 、b 为正实数,故1a b +=,所以2124a b ab +⎛⎫≤= ⎪⎝⎭.当且仅当12a b ==时取等号. 故答案为：14【点睛】本题主要考查了垂径定理的运用以及基本不等式求最值的问题,属于中档题.18．在ABC 中，B 、C 的坐标分别为()-，()，且满足sin sin 2B C A -=，O 为坐标原点，若点P 的坐标为()4,0，则AO AP ⋅的取值范围为__________. 【答案】()12,+∞【解析】由正弦定理可得点A 在曲线221,244x y x -=<-上，设(),A x y ，则224AO AP x x y ⋅=-+，将224y x =-代入可得()2216AO x AP ⋅-=-，利用二次函数的性质可得范围. 【详解】解：由正弦定理得422AC AB BC -===< 则点A 在曲线221,244x y x -=<-上，设(),A x y ，则221,244x y x -=<-，()()224.4,AO AP x y x y y x x --⋅=⋅--=-+，又224y x =-，()22242641AO x AP x x x ∴⋅=--=--+，因为2x <-，则()2221612AO AP ⋅>⨯---=， 即AO AP ⋅的取值范围为()12,+∞. 故答案为：()12,+∞. 【点睛】本题考查双曲线的定义，考查向量数量积的坐标运算，考查学生计算能力，有一定的综合性，但难度不大.三、解答题19．已知数列{}n a 满足：()12311232222122nn n a a a a n +⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+对一切n *∈N 成立.（1）求数列{}n a 的通项公式；（2）求数列21n n a a +⎧⋅⎫⎨⎬⎩⎭的前n 项和n S .【答案】（1）n a n =；（2）()()()35412n n n S n n +=++【解析】（1）先通过1n =求得11a =，再由2n ≥得()123112312222222n n n a a a a n --⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+，和条件中的式子作差可得答案；（2）变形可得2111122n n a a n n +⎛⎫=- ⎪⋅+⎝⎭，通过裂项求和法可得答案.【详解】 （1）()12311232222122n n n a a a a n +⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+①，∴当1n =时，1122a ⋅=，11a ∴=，当2n ≥时，()123112312222222n n n a a a a n --⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+②，①-②得：22n nn a n ⋅=⋅，n a n ∴=，适合11a =，故n a n =； （2）()211111222n na a n n n n +⎛⎫==- ⎪⋅++⎝⎭，11111111121324352n S n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-+-+⋅⋅⋅+- ⎪ ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 111112212n n ⎛⎫=+-- ⎪++⎝⎭()()()35412n n n n +=++.【点睛】本题考查n S 法求数列的通项公式，考查裂项求和，是基础题.20．如图，四棱锥P ABCD -的底面ABCD 中，ABD △为等边三角形，BCD 是等腰三角形，且顶角120BCD ∠=︒，PC BD ⊥，平面PBD ⊥平面ABCD ，M 为PA 中点．（1）求证：DM //平面PBC ；（2）若23AB =PD PB ⊥，求三棱锥P BDM -的体积． 【答案】（1）证明见解析 （2）32【解析】(1)设AB 中点为N ,连接MN 、DN ,再证明平面//DMN 平面PBC ,进而得到DM //平面PBC 即可.(2) 设BD 中点为O ,连接AO 、CO ,根据12P BDM P ABD V V --=,再计算底面ABD △的面积,并证明三棱锥P ABD -的高为PO 计算即可. 【详解】（1）证明：设AB 中点为N ,连接MN 、DNABD 为等边三角形DN AB ∴⊥DC CB =,120DCB ∠=︒30CBD ∴∠=︒603090ABC ∴∠=︒+︒=︒即CB AB ⊥ DN AB ⊥ //DN BC ∴BC ⊂平面PBC ,DN ⊄平面PBC //DN ∴平面PBCMN 为PAB △的中位线//MN PB ∴PB ⊂平面PBC ,MN ⊄平面PBC//MN ∴平面PBCMN 、DN 为平面DMN 内二相交直线∴平面//DMN 平面PBCDM ⊂平面DMN//DM ∴平面PBC ．（2）解：设BD 中点为O ,连接AO 、CO 与POABD 为等边三角形,BCD 是等腰三角形,且顶角120BCD ∠=︒ AO BD ∴⊥,CO BD ⊥A ∴、C 、O 共线PC BD ⊥,BD CO ⊥,PC CO C =,PC ,CO ⊂平面PCOBD ∴⊥平面PCO ．PO ⊂平面PCO BD PO ∴⊥平面PBD ⊥平面ABCD ,交线为BD ,PO ⊂平面PBDPO ∴⊥平面ABCD ．设23AB =3AO ∴=PD PB ⊥,O 为BD 中点132PO BD ∴==111113223622P BDM P ABD ABD V V S PO AO BD PO --∴==⋅⋅⋅=⨯⨯⨯⨯=△．【点睛】本题主要考查了根据面面平行证明线面平行的方法与三棱锥体积的求法,需要根据题意证明线面垂直得到三棱锥的高,再根据平面几何的关系求解面积等.属于中档题. 21．贫困人口全面脱贫是全面建成小康社会的标志性指标．党的十九届四中全会提出“坚决打赢脱贫攻坚战，建立解决相对贫困的长效机制”对当前和下一个阶段的扶贫工作进行了前瞻性的部署，即2020年要通过精准扶贫全面消除绝对贫困，实现全面建成小康社会的奋斗目标．为了响应党的号召，某市对口某贫困乡镇开展扶贫工作．对某种农产品加工生产销售进行指导，经调查知，在一个销售季度内，每售出一吨该产品获利5万元，未售出的商品，每吨亏损2万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如图所示．设该厂在下个销售周期内生产210吨该产品，以x （单位：吨，180230x ≤≤）表示下一个销售周期市场的需求量，Y （单位：万元）表示下一个销售周期市场的销售总利润，视x 分布在各区间内的频率为相应的概率．（1）求实数a 的值；（2）将Y 表示成x 的函数，并求出解析式； （3）估计销售利润不少于910万元的概率． 【答案】（1）0035a =． （2）7420,1802101050,210230x x Y x -≤<⎧=⎨≤≤⎩（3）0.9【解析】(1)根据频率分布直方图的面积之和为1列式求解即可.(2)根据题意,当210x ≥时生产的210吨该产品能全卖完,当210x <时,再利用总收入减去亏损计算即可.(3)根据(2)中的解析式求解910Y ≥时x 的取值范围,再结合频率分布直方图求解概率即可. 【详解】解：（1）由()0.010015003001101a ++++⨯=．．．得：0035a =．．(2)当210x ≥时,21051050Y =⨯=当210x <时,()521027420Y x x x =--⨯=-所以7420,1802101050,210230x x Y x -≤<⎧=⎨≤≤⎩（3）当210230x ≤≤时,1050910Y => 由7420910x -≥得：190x ≥1901001)9(100P x ≥=-⨯=．．∴估计销售利润不少于910万元的概率为0.9．【点睛】本题主要考查了频率分布直方图的理解以及根据分段函数求利润的问题,属于中档题.22．已知椭圆C ：()222210x y a b a b+=>>，右焦点为抛物线24y x =的焦点F .（1）求椭圆C 的标准方程；（2）O 为坐标原点，过O 作两条射线，分别交椭圆于M 、N 两点，若OM 、ON 斜率之积为45-，求证：MON △的面积为定值. 【答案】（1）22154x y +=；（2）见解析 【解析】（1）由条件可得1c =，再根据离心率可求得,a b ，则可得椭圆方程；（2）当MN 与x 轴垂直时，设直线MN 的方程为：()0x t t t =<<≠，与椭圆联立求得,M N 的坐标，通过OM 、ON 斜率之积为45-列方程可得t 的值，进而可得MON △的面积；当MN 与x 轴不垂直时，设()11,M x y ，()22,N x y ，MN 的方程为y kx m =+，与椭圆方程联立，利用韦达定理和OM 、ON 斜率之积为45-可得22254m k =+，再利用弦长公式求出MN ，以及O 到MN 的距离，通过三角形的面积公式求解. 【详解】（1）抛物线24y x =的焦点为()1,0F ，1c ∴=， 55e =，5c a ∴=， 5a ∴=，2b =，∴椭圆方程为22154x y +=；（2）（ⅰ）当MN 与x 轴垂直时，设直线MN的方程为：()0x t t t =<<≠代入22154x y +=得：,M t ⎛ ⎝，,N t ⎛- ⎝，2122455t k k t-∴⋅==-⋅ 2245455t t -∴-⋅=-，解得：252t =，12MONS t ∴=⋅⋅=△ （ⅱ）当MN 与x 轴不垂直时，设()11,M x y ，()22,N x y ，MN 的方程为y kx m =+由()2222245105200154y kx mk x kmx m x y =+⎧⎪⇒+++-=⎨+=⎪⎩， 由22054k m ∆>⇒+>①1221045km x x k +=-+，212252045m x x k-⋅=+ 4·5OM ON k k =-，121245y y x x ∴⋅=-，1212540y y x x ∴+= 即()()22121254550k x x mk x x m +⋅+++=()2222252010545504545m kmk mk m k k-⎛⎫∴+⋅+⋅-+= ⎪++⎝⎭整理得：22254m k =+ 代入①得：0m ≠MN ===O 到MN的距离d =12MON S MN d ∴=△===综上：MON S =△. 【点睛】本题考查椭圆方程的求解，考查直线和椭圆的位置关系，考查韦达定理的应用，考查了学生的计算能力，是中档题.23．已知函数()axf x e x =-（a R ∈，e 为自然对数的底数）．（1）若()f x 有两个零点，求实数a 的取值范围；（2）当()f x 有两个零点1x ，2x ，且12x x <，求证：212x x e ⋅>．【答案】（1）10,e ⎛⎫ ⎪⎝⎭（2）证明见解析【解析】(1)参变分离可知ln xa x =有两个相异实根,再构造函数()ln x G x x=,分析函数的单调性与最值,进而求得函数的取值范围数形结合求解即可.(2) 由题意得1212ax ax e x e x ⎧=⎨=⎩,再运算求得2121ln ln x x a x x -=-,又要证：212x x e ⋅>,只需证12ln ln 2x x +>,代入2121ln ln x x a x x -=-化简可得212122111ln ln ln 1x x x x x x x x ⎛⎫+ ⎪ ⎪+=⋅ ⎪- ⎪⎝⎭,再令21x t x =,构造函数分析单调性与最值证明1ln 21t t t +⎛⎫⋅> ⎪-⎝⎭即可. 【详解】解：（1）()f x 有两个零点⇔关于x 的方程ax e x =有两个相异实根由0>ax e ,知0x >()f x ∴有两个零点ln x a x ⇔=有两个相异实根． 令()ln x G x x =,则()21ln x G x x -'= 由()0G x '>得：0x e <<,由()0G x '<得：x e >()G x ∴在()0,e 单调递增,在(),e +∞单调递减()()max 1G x G e e∴== 又()10G =∴当01x <<时,()0G x <,当1x >时,()0G x >当x →+∞时,()0G x →()f x ∴有两个零点时,实数a 的取值范围为10,e ⎛⎫ ⎪⎝⎭． （2）由题意得1212ax ax e x e x ⎧=⎨=⎩10x ∴>,20x >1122ln ln ax x ax x =⎧∴⎨=⎩ ()1212ln ln a x x x x ∴+=+ ①()2121ln ln a x x x x -=-12x x <2121ln ln x x a x x -∴=- 要证：212x x e ⋅>,只需证12ln ln 2x x +>由①知：()()22112121212221111ln ln ln ln =ln 1x x x x x x x a x x x x x x x x x ⎛⎫+ ⎪- ⎪+=+=⋅+⋅- ⎪- ⎪⎝⎭ 120x x <<211x x ∴> 令21x t x =,1t > ∴只需证1ln 21t t t +⎛⎫⋅> ⎪-⎝⎭1t >101t t +∴>- ∴只需证：()()21ln 1t t t ->+ 令()()()()21F ln 11t t t t t -=->+ ()()()()222114011t F t t t t t -'∴=-=>++ ()F t ∴在()1,+∞递增()()0F t F t ∴>=()()21ln 1t t t -∴>+ 即12ln ln 2x x +>,即212x x e ⋅>．【点睛】本题主要考查了利用导数分析函数的单调性以及求解零点有关的问题,同时也考查了双变量构造函数证明单调性的方法,需要根据题意将参数a 用零点表达,再构造函数分析单调性证明不等式.属于难题.24．已知点A 为圆C ：()2211x y -+=上的动点，O 为坐标原点，过()0,4P 作直线OA 的垂线（当A 、O 重合时，直线OA 约定为y 轴），垂足为M ，以O 为极点，x 轴的正半轴为极轴建立极坐标系.（1）求点M 的轨迹的极坐标方程；（2）直线l 的极坐标方程为sin 43πρθ⎛⎫+= ⎪⎝⎭，连接OA 并延长交l 于B ，求OA OB 的最大值.【答案】（1）4sin ρθ=；（2【解析】（1）设M 的极坐标为(),ρθ，在OPM 中，有4sin ρθ=，即可得结果； （2）设射线OA ：θα=，,22ππα⎛⎫∈- ⎪⎝⎭，圆C 的极坐标方程为2cos ρθ=，联立两个方程，可求出OA ，联立sin 43πρθθα⎧⎛⎫+=⎪ ⎪⎝⎭⎨⎪=⎩可得OB，则计算可得1sin 243OAOB πα⎛⎫=++ ⎪⎝⎭. 【详解】（1）设M 的极坐标为(),ρθ，在OPM 中，有4sin ρθ=， ∴点M 的轨迹的极坐标方程为4sin ρθ=；（2）设射线OA ：θα=，,22ππα⎛⎫∈- ⎪⎝⎭，圆C 的极坐标方程为2cos ρθ=， 由2cos ρθθα=⎧⎨=⎩得：12cos OA ρα==， 由sin 43πρθθα⎧⎛⎫+=⎪ ⎪⎝⎭⎨⎪=⎩得：24sin 3OB ρα==π⎛⎫+ ⎪⎝⎭， 2cos 4sin 3OA OB αα∴=π⎛⎫+ ⎪⎝⎭ 1cos sin 23ααπ⎛⎫=⋅+ ⎪⎝⎭1cos sin sin cos cos sin 233αααππ⎛⎫=+ ⎪⎝⎭21sin cos 4ααα=)1sin 2cos 218αα=++1sin 243πα⎛⎫=+ ⎪⎝⎭， ,22ππα⎛⎫∈- ⎪⎝⎭242333απππ∴-<+<， ∴当232ππα+=，即12πα=时，max OA OB ⎛⎫= ⎪ ⎪⎝⎭，OAOB ∴. 【点睛】本题考查极坐标方程的应用，考查三角函数性质的应用，是中档题.25．已知函数()1f x x =+.（1）求不等式()423f x x ≤--的解集；（2）若正数m 、n 满足2m n mn +=，求证：()()28f m f n +-≥.【答案】（1）{}02x x ≤≤；（2）见解析 【解析】（1）()423f x x ≤--等价于（Ⅰ）()()11234x x x <-⎧⎨-+--≤⎩或（Ⅱ）()()3121234x x x ⎧-≤≤⎪⎨⎪+--≤⎩或（Ⅲ）()()321234x x x ⎧>⎪⎨⎪++-≤⎩，分别解出，再求并集即可； （2）利用基本不等式及2m n mn +=可得28m n +≥，代入()()21212f m f n m n m n +-=++-+≥+可得最值.【详解】（1）()423f x x ≤--等价于（Ⅰ）()()11234x x x <-⎧⎨-+--≤⎩或（Ⅱ）()()3121234x x x ⎧-≤≤⎪⎨⎪+--≤⎩或（Ⅲ）()()321234x x x ⎧>⎪⎨⎪++-≤⎩由（Ⅰ）得：123x x x <-⎧⎪⇒∈∅⎨≥-⎪⎩由（Ⅱ）得：3130220x x x ⎧-≤≤⎪⇒≤≤⎨⎪≥⎩由（Ⅲ）得：332222x x x ⎧>⎪⇒<≤⎨⎪≤⎩. ∴原不等式的解集为{}02x x ≤≤；（2）0m >，0n >，2m n mn +=，()()221122224m n m n m n +∴+=⋅≤⨯， 28m n ∴+≥，当且仅当22m n m n mn =⎧⎨+=⎩，即42m n =⎧⎨=⎩时取等号， ()()212128f m f n m n m n ∴+-=++-+≥+≥，当且仅当210n -+≤即12n ≥时取等号， ()()28f m f n ∴+-≥.【点睛】本题考查分类讨论解绝对值不等式，考查三角不等式的应用及基本不等式的应用，是一道中档题.。