必修2 之 第五章曲线运动 第5节：向心加速度

第五章 曲线运动第一节 曲线运动1.一个质点从平面直角坐标系的原点开始运动并开始计时。

它在t 1时刻到达x 1=2.0m 、y 1=1.5 m 的位置；在t 2时刻到达x 2=3.6cm 、y 2=4.8 m 的位置。

作草图表示质点在0～t 1和0～t 2如时间内发生的位移l 1和l 2，然后计算它们的大小及它们与x 轴的夹角θ1和θ2答：质点两次位移的草图如图所示，根据勾股定理和三角函数的定义可得：l 1 =2.5m, l 2=6.0m ； θ1=arctan(3/4) θ2=arctan(4/3)2.在许多情况下，跳伞员跳伞后最初一段时间降落伞并不张开，跳伞员做加速运动。

随后，降落伞张开，跳伞员做减速运动如图所示。

速度降至一定值后便不再降低，跳伞员以这一速度做匀速运动，直至落地。

无风时某跳伞员竖直下落，着地时速度是5m/s 。

现在有风，风使他以4m/s 的速度沿水平方向向东运动。

他将以多大速度着地?计算并画图说明。

答：根据题意，无风时跳伞员着地的速度为v 2，风的作用使他获得向东的速度v 1，落地速度v 为v 2、v 1的合速度，如图所示。

v 22221245/ 6.4/v v m s m s +=+=与竖直方向的夹角为θ，tan θ=0.8, θ=38.70。

3.跳水运动是一项难度很大又极具观赏性的运动，我国运动员多次在国际跳水赛上摘金夺银，被誉为跳水“梦之队”。

如图是一位跳水队员从高台做“反身翻腾二周半”动作时头部的运动轨迹，最后运动员沿竖直方向以速度v 入水。

整个运动过程中，在哪几个位置头部的速度方向与入水时v 的方向相同?在哪几个位置与v 的方向相反?在图中标出这些位置。

l 12.0 1.53.64.8 l 2 x /m Oy /m答：如图所示，在A 、C 位置头部的速度与入水时速度v 方向相同；在B 、D 位置头部的速度与入水时速度v 方向相反。

4.汽车以恒定的速率绕圆形广场一周用时2 min ，每行驶半周，速度方向改变多少度?汽车每行驶10 s ，速度方向改变多少度?先作一个圆表示汽车运动的轨迹，然后作出汽车在相隔10 s 的两个位置速度矢量的示意图。

向心加速度教学设计长沙县三中：杨平教材分析：本课是人教版高中物理必修2第5章曲线运动的第5节。

是在学习了描述圆周运动的几个物理量后，进一步从运动的角度深入分析物体做圆周运动的特征。

是力和运动知识在圆周运动中的应用，是为解决圆周运动实例分析问题所学的准备知识，也是学习万有引力定律及其应用的知识基础。

本节具有承前启后的重要作用。

学情分析：（1）高一学生认识事物的特点是：开始从具体的形象思维向抽象逻辑思维过渡，但思维还常常与感性经验直接相联系，仍需具体形象的图片、动画来支持。

（2）学生在初中时没有接触过向心加速度的概念。

（3）学生已学习过矢量知识，但将其应用到物理中来，理解上会感到一定的困难，在教学中应注重讲解思想方法，对定量计算不应做具体要求。

教学目标1.通过实验引入和理论引导探究,搞清匀速圆周运动加速度的特点,掌握向心加速度的公式。

2.在实验引入和理论引导探究的过程中,让学生学习科学研究的思想方法。

3.通过对匀速圆周运动加速度的研究,培养学生科学探究的精神，严谨、踏实的治学态度。

德育目标1.领略圆周运动的神奇和谐，发展对科学的好奇心与学习物理知识的求知欲。

2.乐于探究日常生活中的圆周运动所隐藏的物理规律，有将物理知识应用于生产和生活的意识。

3.渗透共性与个性的辩证统一规律。

教学重点1.通过实验感知向心加速度的方向。

2.利用极限思想科学的探究出向心加速度的方向和大小a=rω2=ν2/r。

教学难点向心加速度方向的确定和大小的求解表达式教学资源多媒体、FLASH课件、几何画板、视频【教学流程】教学过程（一）激起探究愿望——引出向心加速度卫星绕地球转动观看视频： 1．提醒学生注意卫星轨迹。

2．提示学生卫星的运动可类比于什么运动？建立模型：轻绳栓一小球,在光滑水平面做匀速圆周运动。

3．引导学生用所学过的描述匀速度圆周运动的物理量去说明小球的运动。

并考虑线速度、角速度、转速、周期是否变化？4．匀速圆周运动是变速运动还是匀速运动？（引出加速度）（二）启发探究思考与实践——探究向心加速度1．怎么研究加速度呢？（提示加速度是联系运动和力的桥梁）2．从力的角度来探究匀速圆周运动的加速度。

第五章 曲线运动第五节 向心加速度一.学习目标：（一）课标要求1．理解速度变化量及向心加速度的概念，2．知道向心加速度和线速度、角速度的关系．3．能够运用向心加速度公式求解有关问题．（二）重、难点1．理解匀速圆周运动中加速度的产生原因，掌握向心加速度的确定方法和计算公式．2．向心加速度方向的确定过程和向心加速度公式的推导与应用．二.巩固基础：1．匀速圆周的向心加速度的物理意义是（ ）A ．它是描述角速度变化快慢的物理量B ．它是描述线速度大小变化快慢的物理量C ．它是描述速度变化快慢的物理量D ．它是描述角速度变化大小的物理量2．下列关于匀速圆周运动的向心加速度，下列说法中错误的是（ ）A ．向心加速度的方向始终与速度的方向垂直B ．向心加速度的方向不断变化C ．向心加速度是恒定的，匀速圆周运动是匀变速曲线运动D ．向心加速度只改变线速度的方向，不改变线速度的大小3．由于地球的自转，地球表面上各点均做匀速圆周运动，下列说法正确的是（ ）A ．地球表面各处具有相同大小的线速度B ．地球表面各处具有相同大小的角速度C ．地球表面各处具有相同大小的向心加速度D ．地球表面各处的向心加速度方向相同4． 如图所示为质点P 、Q 做匀速圆周运动时向心加速度随半径变化的图象，表示质点P 的图象是双曲线，表示质点Q 的图象是过原点的一条直线。

由图象可知（ ）A ．质点P 线速度大小不变B ．质点P 的角速度大小不变C ．质点Q 的角速度随半径变化D ．质点Q 的线速度大小不变 5．做匀速圆周运动的两物体甲和乙，它们的向心加速度分别为a 1和a 2，且a 1＞a 2，下列判断正确的是（ ）A.甲的线速度大于乙的线速度B.甲的角速度比乙的角速度小C.甲的转速比乙的转速小aD.甲、乙的运动周期可能相等6．A 、B 两小球都在水平面上做匀速圆周运动，A 球的轨道半径是B 球轨道半径的2倍，A 的转速为30r/min ，B 的转速为15r/min 。

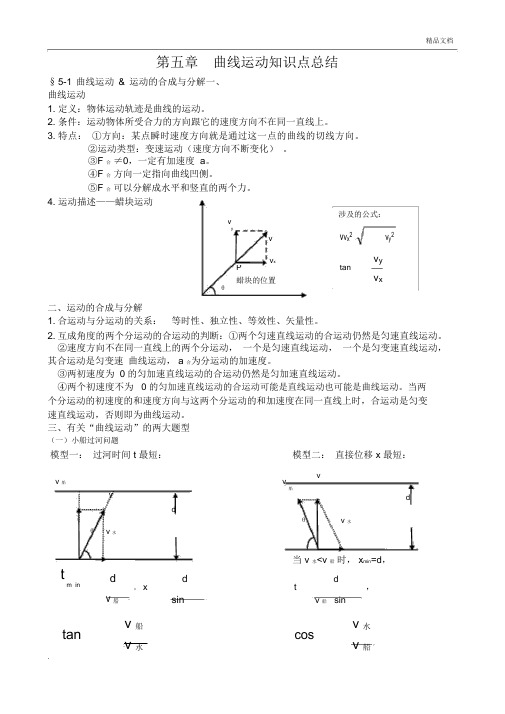
精品文档第五章曲线运动知识点总结§ 5-1 曲线运动 & 运动的合成与分解一、曲线运动1. 定义：物体运动轨迹是曲线的运动。

2. 条件：运动物体所受合力的方向跟它的速度方向不在同一直线上。

3. 特点： ①方向：某点瞬时速度方向就是通过这一点的曲线的切线方向。

②运动类型：变速运动（速度方向不断变化） 。

③F 合 ≠0，一定有加速度 a 。

④F 合 方向一定指向曲线凹侧。

⑤F 合 可以分解成水平和竖直的两个力。

4. 运动描述——蜡块运动涉及的公式：vvyv v x 2v y 2v xv yPtan蜡块的位置v xθ二、运动的合成与分解1. 合运动与分运动的关系： 等时性、独立性、等效性、矢量性。

2. 互成角度的两个分运动的合运动的判断：①两个匀速直线运动的合运动仍然是匀速直线运动。

②速度方向不在同一直线上的两个分运动， 一个是匀速直线运动， 一个是匀变速直线运动，其合运动是匀变速 曲线运动， a 合为分运动的加速度。

③两初速度为 0 的匀加速直线运动的合运动仍然是匀加速直线运动。

④两个初速度不为 0 的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。

当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时，合运动是匀变速直线运动，否则即为曲线运动。

三、有关“曲线运动”的两大题型（一）小船过河问题模型一： 过河时间 t 最短：模型二： 直接位移 x 最短：v 船vvv船ddθv 水θ v 水当 v 水<v 船 时， x min =d ，tm ind d td，v 船， xv 船 sinsintanv 船cosv 水v 水v 船.精品文档模型三：间接位移x 最短：v 船v船dθAθv 水当 v 水>v 船时，x min dcostd，cos v 船 sinsmin(v水 - v船cos )Lv船sin v水L，v船v 船v 水（二）绳杆问题 ( 连带运动问题 )1、实质：合运动的识别与合运动的分解。