当前位置：文档之家 › 非标准Hermite插值的构造

非标准Hermite插值的构造

  • 格式：pdf
  • 大小：86.33 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

2.3插值与逼近之Hermite插值

2.3插值与逼近之Hermite插值

Hermite插值的余项估计
Hermite插值的余项估计
Hermite插值的余项估计
例题
例 设 f (1) 2，f (2) 3，f (1) 1，f (2) 1， 求满足条件的Hermite插值多项式.
解：x0 1, x1 2, h 2 1 1 则 A1 (1 2( x 1))( x 2) 2 (2 x 1)( x 2) 2 A2 (1 2( x 2))( x 1) 2 (2 x 3)( x 1) 2 B1 ( x 1)( x 2) 2 B2 ( x 2)( x 1) 2
2 3
线性空间
{ p( x ) / p( x ) a0 a1 x a2 x 2 a3 x 3}
V span{1, x, x , x }
2 3
span{h0 ( x ), h1 ( x ), H 0 ( x ), H1( x)}
Hermite基函数表
四个插值基函数{h0 ( x), h1( x), H0 ( x), H1( x)}取值如下表：
非标准的Hermite插值
方法二：构造基函数.
基函数 1 0 0 0 函数值 0 1 0 0 0 0 1 0
2
导数值 0 0 0 1
h2 ( x) k ( x x1 ) ( x x0 )
2
( x x1 ) ( x x0 ) h2 ( x ) ( x2 x1 )2 ( x2 x0 )
Hermite基函数表
基函数 函数值 导数值
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
h1( x) (a bx)( x xi )2

Hermit插值

Hermit插值
2 42 4 2
-0.5 -0.75 0.5 -0.75 0 0.5 -0.75 1 1
2 3 2.5 1 0
p3(x)3 4(x1 2)(x1 2)x21
18
†误差估计：
定理 5.3 设 x0, x1, , xn是互异的实数，对于给定的 x，是 函数 f (t)在区间I x具体m n 2阶导数，Hmn1(x)是满足 插值条件的 Hermite 多项式，则用Hmn1(x)近似代替 f (x) 的余项为
上，有
h1 ( x)
（1
（2 x
x1）
l（1
x1）
）
l
2（ 1
x
）
h2 (
x)
（1
（2 x
x2）
l（2
x
）
2
）
l
2（ 2
x
）
h1 (
x)
（x
x1）
l
2（ 1
x
）
h2 (
x)
（x
x
）
2
l
2（ 2
x
）
其中
l1(x)xx1xx22， l'1(x)x1 1x2
l2(x)xx2xx11， l'2(x)x21x1
1 i j
(2)h 'i ( x j )
ij
0
i j
hi ( x j ) 0 (i， j 0，1，2， ， n)
设 h i(x ) (c x d )l2 i(x )
由 条 件 (2)可 列 出 方 程 组
h'i(h x i(i)x i)c li2 ((cx xii) d 2 )(lc i2 x (ix i)d )l0 i(xi)li'(xi)1

埃尔米特插值

埃尔米特插值

0，则可以设：
0(x) (x 1)(ax b)
将：
0 (0) 1
0
(0)
0
带入0(x) (x 1)(ax b)，则：
a 1 b 1
则：0 (x) 1 x2
同理： 1( x)为二次项式
又：
1(0) 0
1
(0)
0
则：x 0为1(x)的二重根
则：1(x) cx2 又：1(1) 1
xi
01
f(xi) 0
1
f (xi )
0
1
解: 本题利用承袭性的思想 首先利用:
xi
0
1
f(xi) 0
1
求出: L1(x)
L1 ( x)
x x1 x0 x1
y0
x x0 x1 x0
y1
x
增加:
xi 0
yi 0
求：H2 ( x), 其中H2 ( x)满足：
xi
01
f(xi) 0
1
f (xi )
则：c 1
则：1(x) x2 同理：0 (x) x(1 x)
插值余项为:
R(x)
f (x) H2(x)
f
(
3!
)
(
x
x0
)2
(
x
x1 )
仿Lagrange 或 Newton 证明
情形2. 已知: 4个条件
xi
x0 x1
yi = f(xi) y0 y1
yi f (xi ) y0 y1
一、 Hermite插值多项式的定义
插值条件中除函数值外, 还有导数值（回顾 Taylor展开式, 是某点的导数值）, 如
已知: 2n+2个条件

埃尔米特(Hermite)插值

埃尔米特(Hermite)插值

实验二埃尔米特（Hermite）插值一、实验目的：1.掌握埃尔米特插值算法原理；2.使用C语言编程实现埃尔米特插值算法。

二、实验准备：阅读《数值分析》2.4节二、实验要求：某人从甲地开车去乙地，每隔一段时间对行车距离和速率进行一次采样，得到在n+1 个采样时刻点t i 的里程s i和速率v i（i=0, 1, ..., n）。

要求编程构造埃尔米特插值多项式H2n+1(t)，满足H2n+1(t i)=s i，H'2n+1(t i)=v i，对所有i=0, 1, ..., n成立，并据此计算m个给定时刻的里程和速率。

函数接口定义：void Hermite_Interpolation( int N, double t[], double s[], double v[], int m, double ht[], double hs[], double hv[] );其中N为采样点个数（注意这个N不是公式中的最大下标n，而是等于n+1），采样时刻点t i、里程s i、速率v i分别通过t、s、v传入；m是需要估算的给定时刻的个数，ht传入给定的时刻点，相应计算出的里程和速率应分别存储在hs和hv中。

裁判程序如下：裁判输入数据：20.0 1.00.0 1.00.0 0.050.0 0.2 0.5 0.8 1.030.0 0.5 1.0100.0 170.0 200.030.0 150.0 0.050.0 0.25 0.5 0.75 1.050.0 1.0 2.0 3.0 4.00.0 60.0 160.0 260.0 300.05.0 70.0 100.0 120.0 20.0100.5 1.0 1.5 2.0 2.5 3.0 3.5 3.8 3.95 4.0标准输出数据：0.0000 0.1040 0.5000 0.8960 1.00000.0000 0.9600 1.5000 0.9600 0.0000100.0000 127.9297 170.0000 195.9766 200.000030.0000 165.4688 150.0000 52.9688 0.000030.2222 60.0000 105.9303 160.0000 206.3438 260.0000 307.9764 305.7687 299.9796 300.000062.6024 70.0000 109.0488 100.0000 92.9745 120.0000 41.2374 -44.8421 -16.2783 20.0000#include<stdio.h>#define MAXN 5 /* 最大采样点个数 */#define MAXM 10 /* 最大估算点个数 */void Hermite_Interpolation( int N, double t[], double s[], double v[], int m, double ht[], double hs[], double hv[] ){double l[10],p[10],h1[10],h2[10],x,ll[10],pp[10];int kk;for(kk=0;kk<m;kk++){x=ht[kk];hs[kk]=0;hv[kk]=0;int i;for(i=0;i<N;i++){l[i]=1;ll[i]=1;int j;for(j=0;j<N;j++){if(i!=j){l[i]=l[i]*(x-t[j])/(t[i]-t[j]);}}p[i]=0;pp[i]=0;int k;for(k=0;k<N;k++){if(i!=k){p[i]=p[i]+l[i]/(x-t[k]);pp[i]=pp[i]+ll[i]/(t[i]-t[k]);}}h1[i]=(1-2*pp[i]*(x-t[i]))*l[i]*l[i];h2[i]=(x-t[i])*l[i]*l[i];hs[kk]=hs[kk]+s[i]*h1[i]+v[i]*h2[i];int kkk;for(kkk=0;kkk<N;kkk++){if(x==t[kkk])break;}if(x==t[kkk])hv[kk]=v[kkk];elsehv[kk]=hv[kk]+s[i]*(2*p[i]*l[i]-4*l[i]*p[i]*(x-t[i])*pp[i]-2*pp[i]*l[ i]*l[i])+v[i]*(l[i]*l[i]+2*l[i]*p[i]*(x-t[i]));}}}int main(){int N, m;double t[MAXN], s[MAXN], v[MAXN]; /* 用于构造的数据 */double ht[MAXM], hs[MAXM], hv[MAXM]; /* 用估算的数据 */int i;while ( scanf("%d", &N) != EOF ) {for ( i=0; i<N; i++ )scanf("%lf", &t[i]);for ( i=0; i<N; i++ )scanf("%lf", &s[i]);for ( i=0; i<N; i++ )scanf("%lf", &v[i]);scanf("%d", &m);for ( i=0; i<m; i++ )scanf("%lf", &ht[i]);Hermite_Interpolation( N, t, s, v, m, ht, hs, hv );for ( i=0; i<m; i++ )printf("%.4lf ", hs[i]);printf("\n");for ( i=0; i<m; i++ )printf("%.4lf ", hv[i]);printf("\n\n");}return 0; }。

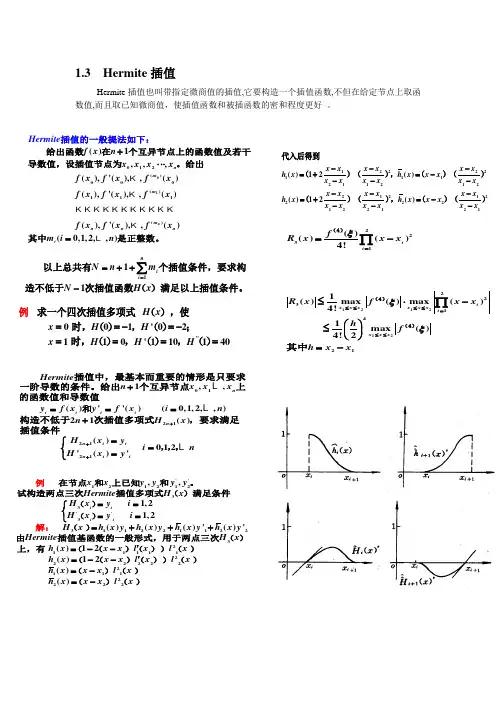
hermite插值

hermite插值

1.3 Hermite 插值Hermite 插值也叫带指定微商值的插值,它要构造一个插值函数,不但在给定节点上取函数值,而且取已知微商值，使插值函数和被插函数的密和程度更好 。

01012()000()111()()1,,,(),'(),,()(),'(),,()(),'(),,()(0,1,2,,)n n m m m n n ni H f x n x x x x f x f x f x f x erm f x f x f x f x it f x m i n e +⋅⋅⋅=插值的一般提法如下给出函数在个互异节点上的函数值及若干导数值，设插值节点为。

给出其中是：正整数。

111ni i N n m N H x ==++-∑以上总共有个插值条件，要求构造不低于次插值函数（）满足以上插值条件。

''001'02110'110140H x x H H x H H H ==-=-====求一个四次插值多项式（），使 时，（），（）； 时，（），（），（）例012121211,,()''()(0,1,2,,)21()()012'()'n i i i i n n i in ii Hermite n x x x y f x y f x i n n H x H x y i n H x y ++++===+=⎧=⎨=⎩插值中，最基本而重要的情形是只要求一阶导数的条件。

给出个互异节点上的函数值和导数值和构造不低于次插值多项式，要求满足插值条件，，，''12121233''331122112232111112,,1,21,2()()()'()'()12()1i i i i x x y y y y Hermite H x H x y i H x y i H x h x y h x y h x y h x y Hermite H x h x x x l x l x h x ==⎧⎨==⎩=+++'=--=-在节点和上已知和。

Hermite_插值法

Hermite_插值法

, x0]
lim
xi x0
f [x0, x1,
,
xn ]
1 n!
f
(n) ( x0 )
重节点Newton插值
在 Newton 插值公式中，令 xi x0 , i = 1, … , n, 则
Nn( x) f ( x0 ) f [ x0 , x1]( x x0 )
f ( x0 ) f '( x0 )( x x0 )
( x1 x0 )( x1 x2 )
三点三次Hermite 插值
余项公式
由于 x0 , x1 , x2 是 R(x) 的零点，且 x1 是二重零点，故可设 R( x) f ( x) P( x) k( x)( x x0 )( x x1 )2 ( x x2 )
与 Lagrange 插值余项公式的推导过程类似，可得
x
x0
)
x x0
x1 x1
2
1(
x)
(
x
x1
)
x x1
x0 x0
两点三次Hermite 插值
满足插值条件
P(x0) = f(x0) = y0，P’(x0) = f’(x0) = m0 P(x1) = f(x1) = y1，P’(x1) = f’(x1) = m1
的三次 Hermite 插值多项式为
三点三次Hermite 插值
三点三次 Hermite 插值
插值节点：x0 , x1 , x2
插值条件：P(xi) = f(xi)，i = 0, 1, 2，P’(x1) = f’(x1) 设 P( x) f ( x0 ) f [x0, x1]( x x0 )
f [ x0, x1, x2]( x x0 )( x x1) A( x x0 )( x x1 )( x x2 ) 将 P’(x1) = f’(x1) 代入可得 A f '( x1 ) f [ x0 , x1] f [ x0, x1, x2]( x1 x0 )

5.2Hermite插值

5.2Hermite插值

六、分段Hermite插值 （与学生一起看书学习） 6.6 分段Hermite插值（任玉杰） 1、分段Hermite插值函数（408页） （1）定义6.4（分段三次Hermite插值函数）
分段三次Hermite插值函数与一般的Hermite插值的区别：
设在节点 a x0 x1 xn b 上,
r ( xi ) 0, i 0,1,2,, n r ( xik ) 0, k 0,1,2,, m
r ( x) 的零点个数m+n+2个.
r ( x) 0
四、Hermite插值多项式的构造 设在节点 a x0 x1 xn b 上,
yi f xi , yi f xi i 0,1, n
0 ( x) y1 1 ( x) H3 ( x) y00 ( x) y11 ( x) y0
H 2 n1 x y j j x yj j x .
j 0 n
n 1 2 j x 1 2 x x j l j x. k 0 x j xk k j
提示：令
j ( x) (ax b)l 2 j ( x), j ( x) (cx d )l 2 j ( x),
例：求满足条件：
f x0 , y1 f x1 , y1 f x1 y0 f x0 , y0
的三次Hermite插值多项式 H 3 ( x) 。
要求插值多项式 H x ,满足条件
① H xi yi , H xi yi i 0,1, n .
1 H x C [a, b] ②
③在每个子区间 [ xi 1 , xi ] 上为三次多项式。 （2）分段三次Hermite插值多项式的形式

第三章 插值法 Hermite插值

第三章 插值法 Hermite插值

, H3 ( xk1 ) yk1 , H'3 ( xk1 ) mk1
H3(x) 存在且唯一，表达式为
f '( x) mk
(5.8)
mk 1
H3 ( x) ykk ( x) yk1 k1( x) mk k ( x) mk1k1( x) (5.9)
其中
k ( x)
(1
2
x xk xk1 xk
则可令 j (x) A(x xj )(x x0)2(x x1)2 (x xj1)2(x xj1)2 (x xn )2
又由 j ( x j ) 1 ，则有 1 j ( xj ) A(xj x0)2(xj x1)2 ( xj xj1)2( xj xj1)2 (xj xn )2
lj
n1
xj)
i0
xj
xi
i j
(x x j )l
nx
(x)
x i 0
i j
j
)l
2 j
(
x
)；
2 j
(
x)；
xi xi
余项公式为:
R3( x)
f (x) H3(x)
f
(4) (
4!
)
(
x
xk
)2
(
x
xk 1
)2
x x0 x1 x2
例 已知 y f (x) 函数表及导数表 f ( x) y0 y1 y2
f ( x)
f1
求次数不超过3的多项式 P3 ( x) 使满足插值条件：
分析
P3 ( p'3
xi ) ( x1
yi ,(i ) f '1
0,1,2)
已知 ( x0 , y0 ), ( x1, y1 ), ( x2 , y2 ) 三点，由牛顿插值多项式，

插值法-Hermite插值专业知识

插值法-Hermite插值专业知识

共有m+1个条件
其中 xi (i 0,1,, n) 互异，mi为正整数，记 mi m 1，
谋求m次多项式P(x)使满足插值条件：
i0
P(k)( xi ) f (k)( xi ), (i 0,1,, n;k 0,1,, mi 1) (5.1)
埃尔米特Hermite插值问题
我们只讨论 P( xi ) f ( xi ), P( xi ) f ( xi ) 旳情形。
(5.5)
其中
j
(
x),
j
(
j0
x),( j
0,1,,
n)为Hermite插值基函数,即
j(x)
(1
2( x
n
xj)
i0
xj
1
xi
)l
2 j
(
x
)；
i j
j
(
x)
(
x
x
j
)l
2 j
(
x)；
n
l
j
(x)
n
i0 i j
x xi x j xi
实际上,有 H 2n1 ( xi ) ( j ( xi ) yi j ( xi ) y' j ) yi
j
(
x)
(1
c(
x
x
j
))
(((xxxxx000))222((xx xx11))222(((xxxxxjjj11))22((xx xxjj11))22((xx xxnn))22
((xxjj
xx00))22((xxjj
xx11))22((xxjj
xxjj11))22((xx
jj
xx
))22
jj11

第五节Hermite插值

第五节Hermite插值

多项式, f(x)在含xi的区间[a,b]上2n+2阶连续可微, 则对任意
的x[a,b],总存在 (a,b),使得
f ( 2 n 2) ( ) 2 R( x) f ( x) H 2 n 1 ( x) ( x ) (5.6) (2n 2)!
6 例 求满足 P( x j ) f ( x j )
'
( j 0,1,, n)
与前面讨论类似，可证明满足条件的Hermite 插值多项式 是存在唯一的，其余项为
10
m f ( m n 2) ( ) R( x) f ( x) H ( x) n1 ( x) ( x x jk ) (m n 2)! k 0
例：按下表求Hermite 插值多项式
( j 0,1,2) 及 P' ( x j ) f ' ( x j )
的插值多项式及其余项表达式。
由给定条件，可确定次数不超过3 的插值多项式。
由于此多项式通过点
( x0 , f ( x0 )),
故其形式为
( x1 , f ( x1 )) 及 ( x2 , f ( x2 ))
P( x) f ( x0 ) f [ x0 , x1 ]( x x0 )
n 2 i n
(5.5)
H 2 n 1 ( x) [1 2( x xi )li ( xi )]l ( x) yi ( x xi )li2 ( x) yi
i 0 i 0
{[1 2( x xi )li ( xi )] yi ( x xi ) yi}li2 ( x)
f [ x0 , x1 , x2 ]( x x0 )( x x2 )
A( x x0 )( x x1 )( x x2 )

基于非规则Hermite型插值多项式的几种解法

基于非规则Hermite型插值多项式的几种解法

基于非规则Hermite型插值多项式的几种解法
马亮亮;田富鹏
【期刊名称】《陇东学院学报》
【年(卷),期】2010(021)002
【摘要】基于埃尔米特型插值多项式,针对比较复杂的非规则埃尔米特型插值多项式,给出了包括待定系数法、Lagrange插值法、基函数法、重差商法等几种解决此类插值多项式的方法.
【总页数】5页(P13-17)
【作者】马亮亮;田富鹏
【作者单位】西北民族大学,计信学院,甘肃,兰州,730030;西北民族大学,计信学院,甘肃,兰州,730030
【正文语种】中文
【中图分类】O212.4
【相关文献】
1.关于一个修正型的Hermite插值多项式 [J], 何甲兴
2.基于Hermite插值多项式的可验证多秘密共享方案 [J], 谭晓青;王治国
3.几种Hermite插值多项式存在唯一性的另一种368-04证明方法及推广的基函数构造方法 [J], 张引娣;封建湖
4.基于Hermite插值多项式的光伏MPPT改进算法的研究 [J], 罗驰;任一峰;安坤;李涛;张泽慧
5.带有(1-X^2)P_(n-1)′(X)零点的修正型Hermite插值多项式 [J], 王国明;张朝凤
因版权原因，仅展示原文概要，查看原文内容请购买。

非标准hermite插值二阶导数

非标准hermite插值二阶导数

非标准hermite插值二阶导数
我们要计算非标准Hermite插值的二阶导数。

首先，我们需要了解什么是非标准Hermite插值。

非标准Hermite插值是一种数学方法，用于通过给定的数据点来估计一个函数的值。

它与标准Hermite插值的主要区别在于，非标准Hermite插值允许我们为数据点指定导数值。

假设我们有一个函数f(x)，并且我们知道在某些点x0, x1, ..., xn处的函数值和导数值。

非标准Hermite插值将使用这些信息来估计在其他点x上的函数值，同时保持与原始数据点的连续性和光滑性。

对于二阶导数的计算，我们需要使用Hermite插值的二阶导数公式。

但是，由于这是一个非标准插值，我们需要考虑给定的导数值的影响。

假设我们有一个数据点(xi, yi, di, dii)，其中di是yi的导数，dii是yi的二阶导数。

那么，对于非标准Hermite插值的二阶导数，我们需要使用以下公式：
d'ii[y(xi)] = dii + (xi - xi) [d'i[y(xi)] - di] / (xi - xi)
其中，d'i[y(xi)]是y(xi)的一阶导数。

这个公式考虑了给定的二阶导数值和一阶导数值，使得插值结果在保持连续性和光滑性的同时，尽可能接近原始数据点的二阶导数值。

因此，对于非标准Hermite插值的二阶导数，我们需要使用上述公式来计算。

这个公式将确保插值结果在保持连续性和光滑性的同时，尽可能接近原始数据点的二阶导数值。

计算方法 13 Hermite插值资料

计算方法 13 Hermite插值资料

x x1
x0 x0
2
(x
x1 )l1( x)2.
记 h x1 x0
A0 (x)
1
2
x
x0 h
1
x
x0 h
2
A1 ( x)
3
2
x
x0 h
x
x0 h
2
B0 (x)
h
x
x0 h
1
x
x0 h
2
B1 ( x)
h
x
x0 h
1 x
x0
2
h
置 x0 0, x1 1，则
观察上面的条件，可知
n个插值节点xk , k 0,1,, n, k j是插值基函数Aj (x)的二重 零点, 而x j不是Aj (x)的零点，然而基函数Aj (x)是2n 1次多项 式。故我们可以假设
Aj ( x) D j (ax b)( x x0 )2 ( x x j1 )2 ( x x j1 )2 ( x xn )2
A0 ( x)
x0
x1
B0 ( x)
x0
x1
A1( x)
Bj (x) (x x j ) l j (x) 2
再构造 Aj ( x) ： 由于第一个方程用于确定与函数值相关的条件，因此，有
Aj ( xk ) 0, k 0,1,, n, 且k j; Aj ( xk ) 1, k j.
而第二个方程用于确定与导数值相关的条件，因此，有
Aj ( xk ) 0, k 0,1,, n.
令
n
n
H 2n1( x) Aj ( x) y j B j ( x) yj ,
j0
j0
其中插值基函数 Aj ( x) ，B j ( x) 都是 2n 1 次式。由于 插值问题的解存在唯一性定理，有

Hermite插值法

Hermite插值法
′ ′ R3 ( xi ) = f ′( xi ) − H 3 ( xi ) = 0
i = 0 ,1
x0 , x1均为R3 ( x )的二重零点,因此可设
R3 ( x ) = K ( x )( x − x0 )2 ( x − x1 )2
其中K (x )待定
10
构造辅助函数
ϕ (t ) = f (t ) − H 3 (t ) − K ( x )(t − x0 )2 (t − x1 )2
求一个次数不超过2n+1次的多项式H(x)使 求一个次数不超过2n+1次的多项式H(x)使 2n+1次的多项式H(x)
H ( xi ) = f ( xi ) = yi H ′( xi ) = f ′( xi ) = yi′
i = 0 ,1,L , n i = 0 ,1,L , n
这种带有导 数的多项式 问题， 插值 问题， 称为 Hermite插 Hermite插 值问题。 值问题。 1
′ ′ H 3 ( x) = y0α 0 ( x) + y1α1 ( x) + y0 β 0 ( x) + y1β1 ( x)
线性插值基函数代入定理1.5 将Lagrange线性插值基函数代入定理 线性插值基函数代入定理 中的基函数求得三次Hermite插值的基 中的基函数求得三次 插值的基 函数! 函数
x − x1 l0 ( x) = x0 − x1 x − x0 l1 ( x) = x1 − x0
基函数具有 什么表达式？ 什么表达式？
4
x − x0 x − x1 α 0 ( x) = 1 + 2 x1 − x0 x0 − x1
2
x − x1 x − x0 α1 ( x ) = 1 + 2 x0 − x1 x1 − x0

数值分析(13)Hermite插值

数值分析(13)Hermite插值
' i
a 2li' ( xi ) 解出 ' b 1 2 x l i i ( xi )
hi ( x ) (1 2( x xi )li' ( xi )) l i2 ( xi ) ( i 0,1, 2, n) n n x xj 1 ' 其中 li ( x ) ( ), l i ( xi ) ( ) xi x j xi x j j0 j0 所以
2n
共2n 2个方程，可求出2n 2个系数a0 , a1 ,..., a2n , a2n1 .
数值分析
数值分析
Hermite插值多项式的构造
( 2) Lagrange型插值基函数法 设Hermite插值多项式为 H 2 n1 ( x ) hi ( x ) yi hi ( x ) y 'i
数值分析
数值分析
由条件(2)可列出方程组 2 h ( x ) ( cx d ) l i i i i ( xi ) 0 2 ' h ' ( x ) cl ( x ) 2( cx d ) l ( x ) l i i i i i i i i ( xi ) 1
li ( xi ) 1, cxi d 0, c 1 解出 d xi 于是求出
i 0
数值分析
n
2
F ( t )关于t 有n 2个零点：x0，x1， ，xn，x 。 但F ' ( t )关于t 有2n 2个零点，由Rolle(罗尔)定理 必存在点 （a , b），使 F
（2 n 2）
( ) f
（2 n 2）
( ) 0 K ( x )(2n 2)! 0

5.4埃尔米特(Hermite)插值

5.4埃尔米特(Hermite)插值

n
计算方法
H2n+1(x)为满足条件
H ( xi ) f ( xi ),
H ( xi ) f ( xi )
( i 0,1, , n)
的2n+1次Hermite插值多项式。
计算方法
定理
满足插值条件
H ( xi ) f ( xi ) ( i 0,1, , n)
H ( xi ) f ( xi ),
计算方法
§5.4 埃尔米特(Hermite)插值
许多实际问题不但要求插值函数p(x)在插值节
点处与被插函数f(x)有相同的函数值p(xi)=f(xi) (i=0,1,2,…,n), 而且要求在有些节点或全部节点上 与f(x)的导数值也相等，甚至要求高阶导数值也相 等，能满足这种要求的插值问题就称为埃尔米特
i( x j ) 0 i ( x j ) 0
(i, j =0,1,2, …,n)
Hermite插值多项式可写成插值基函数表示的形式
H 2 n1 ( x ) i ( x ) f ( xi ) i ( x ) f ( xi )
i 0
n
计算方法
验证：
H 2n1 ( x j ) i ( x j ) f ( xi ) i ( x j ) f ( xi ) ij f ( xi ) 0 f ( x j )
i 0 i 0
n
n

0 ij f ( x j ) f ( x j )
i 0
n
计算方法
根据插值条件可求出 j ( x ) 和 j ( x )( j 0,1, n)
n 1 2 1 2( x x ) j ( x) l j ( x) j k 0 x j xk k j
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

归纳法可以证明 ,对于 n重节点可类似定义
f x0 , …, x0
f( n - 1) =
( x0 )构造差商表
( n - 1) !
0
0
0
0
0
1
1
1
1
1
1
2
1
0
1
0
-1
- 1 - 1 /2 1 /4
由牛顿插值多项式得 P4 ( x) = x2 - x2 - ( x - 1) +
1 x2 ( x - 1) 2 = 1 x2 ( x - 3) 2
〔责任编校 :李建明 英文校对 :徐常兰 〕
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
再由待定系数求解. 本题可以看成是拉格朗日插值
再附加 x = 0, x1 = 1 的导数值而得.
先求得满足 f ( 0) = 0 , f ( 1) = 1, f ( 2 ) = 1 的拉
格朗日插值多项式
P2 ( x - 1)
=-
1 x2 2
+
3 2
x, 再设
P4 ( x) = P2 ( x) + (A x +B ) ( x - 0) ( x - 1) ( x - 2) , 则
4
4
注 :对差商运算熟悉后 ,这种方法最为简洁.
3 应用
例 2 构造插值多项式 ,使之满足 f ( 0) = 2 ,
f ( 1) = 1, f ( 2) = 2, f′( 0) = - 2, f′( 1) = - 1,
f ′( 0) = - 10 (见文献 [ 3 ]中 )我们用方法五 , 构造差
商表如下 :
The con struct of abnorma l Herm it in terpola ting m ethod
YANG Hong - qiang (M athematics and Computor Department, Hengshui University, Hengshui, Hebei 053000, China) Abstract: Interpolating methods have app lied broadly, while the construction of abnormal Herm ite interpolating method has not a better conclusion. For a better understanding of it, the paper gives five methods in different angles and expands the solutions of the confer2 ences. Key words: herm it interpolating; interpolating methods; interpolation.
方法二 :直接构造插值基函数. 记 x0 = 0, x1 = 1, x2 = 2. 设 P4 ( x) = y0 I0 ( x) + y1 I1 ( x) + y2 I2 ( x) + y0 β′0 ( x) + y1 β′1′( x). s
其中 , Ii ( x) 、βj ( x) ( i = 0, 1, 2, j = 0, 1)均为次数不 超过 4的多项式 ,且满足条件
(x
-
2)
,β1
(x)
=
-
x2
( x - 1)
(x -
2). 计算得
P4
( x)
=
1 x2 4
(x -
3) 2.
注 1:本题思想是借鉴拉格朗日插值函数的构
造方法而得. 对于非标准 Herm ite插值的构造 ,具有
普遍意义.
注 2:对于本题中的条件 f ( 0) = f′( 0) = 0, 在实
际求解过程中可以不求出
I0
( x)
,
β 0
( x)来从而简化
运算.
方法三 :先求出 Herm ite插值 ,然后由待定系数
构造.
本题可以认为是一个三次 Herm ite插值再加上
条件复合而得. 故可以认为由三次 Herm ite 插值扩
展而得.
先做满足 f ( 0 ) = f′( 0 ) = 0, f ( 1 ) = f′1 ) = 1 的
函数值
导数值
x0
x1
x2
x0
x1
I0 ( x)
1
0
0
0
0
I1 ( x)
0
1
0
0
0
I1 ( x)
0
0
1
0
0
β0 ( x)
0
0
0
1
0
β1 ( x)
0
0
0
0
1
s由上表可知 ,
l0 ( x) = ( ax + b) ( x - 1) 2 ( x - 2) ,
I1 ( x) = ( cx + d) x2 ( x - 2) , I2 ( x) = ex2 ( x - 1) 2 ,
x1
由导数定义可知 , lim x →x 0
f ( x) - f ( x0 ) x →x0
=
f′( x0 ) ,定义差商 f x0 , x0
= lim x →x 0
f ( x) - f ( x0 ) x →x0
,则
f x0 , x0 = f′( x0 ) , 同理 f x1 , x1 = f′( x1 ) (由数学
0
2
0
2 -2
0
2 -2 -5
1
1 -1 1
6
1
1 -1 0 -1 -7
2
2
1
2
1
14
则 P5 ( x) = 2 - 2x - 5x2 + 6x3 - 7x3 ( x - 1) + 4x3 ( x - 1) 2 = 4x5 - 15x4 + 17x3 - 5x2 - 2x + 2
例 3 构造插值多项式 , 使之满足 f ( 1 ) = 2, f ( 2) = 4, f ( 3) = 12, f′( 2) = 3 . (见文献 [ 3 ]中 )可以 用方法四 、五求解.
该问题带有导数 ,但在节点 x = 2未给出导数值 ,
属于非标准的带导数插值 ,我们称之为非标准的 Her2 m ite插值 ,对于这类问题并没有给出统一的解法 ,下面
我们可以通过五种途径来解决它.
2 解法
方法一 :构造四次多项式 P4 ( x) ,并通过解方程组 来求解. 在文献 [1]中已给出解答.
P4 (x)满足
P2 (x)的插值条件 ,再由条件
P′4 ( 0)
=
3 2
&#=
1 2
-
(A
+B )
= 1可得
A
=
1 4
,
B
=
-
3 4
, 因此
P4 ( x)
=
-
1 x2 ( x - 3) 2. 4
注 :该方法对于导数条件多的待定系数的方程
组的运算较为复杂 , 但对于拉格朗日插值附加一个
β 0
( x)
=Ax (x -
1) 2
(x -
2) ,β1 ( x)
=B x2
(x -
2).
解出待定系数代入可得
I0 ( x) =
-
5 4
x
-
1 2
, I1 ( x)
= x2 ( x - 2) 2 ,
I2 ( x)
=
1 ( x) 2 ( x - 1) 2 , 4
β 0
( x)
=-
1 2
x
(x
-
1) 2
1 问题提出 插值法是应用广泛的一种方法 ,对于要求函数
有微商值的常用三次 Herm ite插值来解决 ,在文献
中也给出构造方法 ,它要求在给定节点上取函数值 ,
并且取导数值. 而如下问题
例 1构造插值多项式 ,使之满足 f (0) = f′(0) = 0, f (1) = f′(1) = 1, f (2) = 1.
摘 要 :插值法有广泛的应用 ,而非标准 Herm ite插值的构造尚无更好的结论. 为了对这一问题进一步了解 ,对文献所提问题
从不同角度出发 ,得到了五种有效方法 ,大大拓展了文献中的解法.
关键词 : Herm ite插值 ;插值 ;差商 中图分类号 : O174. 42 文献标识码 : A 文章编号 : 1673 - 2065 (2007) 01 - 0055 - 02
5 6 衡水学院学报 第 9卷
P4 ( x)
= x2 ( 2 -
x)
+
1 x2 ( x 4
1) 2
=
1 x2 ( x 4
3) 2
注 :本方法对 Herm ite 插值附加一个函数值的
情况易于计算.
方法四 :先求牛顿型或拉格朗日型插值多项式 ,
Herm ite插值多项式 H3 ( x) ,由文献 [ 2 ]中所给公式 可计算出 H3 ( x) = x2 ( 2 - x) ,再设 P4 ( x) = H3 ( x) + A x2 ,则 P4 ( x)满足 H3 ( x) 的插值条件 ,再由 P4 ( 2) =
H3 ( 2)
+ 4A = 1, 而
参考文献 :
[ 1 ] 华中理工大学数学系. 计算方法 [M ]. 北京 :高等教育 出版社 ,施普林格出版社. 1999: 59.