2.4 Hermite插值多项式

一类四次hermite插值多项式逼近的最佳常函数估计一类四次hermite插值多项式逼近的最佳常函数估计四次hermite插值多项式逼近是指用多项式逼近某一类常函数，其中hermite插值多项式是由插值点处的函数值和导数值求得的。

在逼近过程中，为了使逼近误差最小，通常采用最佳常函数估计的方法。

最佳常函数估计的思想是，在满足一定条件的情况下，找到一类函数，使得这一类函数在所有可能的常函数中，其逼近误差最小。

四次hermite插值多项式逼近最佳常函数估计的具体方法如下:1. 选择插值点在四次hermite插值多项式逼近中，首先要选择插值点。

一般来说，插值点的选择应当满足等距或等比分布的原则。

这样可以使逼近误差均匀分布，从而使得最终的逼近效果最优。

2. 求解hermite插值多项式在选择了插值点之后，就可以开始求解hermite插值多项式了。

这一步的具体方法是，根据插值点处的函数值和导数值，求解hermite插值多项式的系数。

3. 计算逼近误差在求得her插值多项式之后，就可以开始计算逼近误差了。

逼近误差是指多项式逼近函数时所产生的误差。

计算逼近误差的具体方法是，在所有的插值点处分别计算多项式和函数的差值，然后取这些差值的最大值。

这个最大值就是逼近误差。

4. 比较逼近效果在计算出逼近误差之后，就可以比较多项式逼近函数的效果了。

如果逼近误差较小，说明多项式逼近函数的效果较好；如果逼近误差较大，则说明多项式逼近函数的效果较差。

四次hermite插值多项式逼近最佳常函数估计的方法介绍到这里。

总的来说，四次hermite插值多项式逼近是一种非常有效的方法，可以用来逼近各种常函数。

hermitage插值法【实用版】目录1.概述 Hermite 插值法2.Hermite 插值法的基本原理3.Hermite 插值法的应用实例4.Hermite 插值法的优点与局限性正文1.概述 Hermite 插值法Hermite 插值法是一种基于分段多项式的插值方法，用于在给定区间内对已知数据点进行插值。

它是一种三次样条插值法，可以提供比其他低阶插值方法更精确的结果。

Hermite 插值法的名称来自于法国数学家Charles Hermite，他在 19 世纪末开发了这种方法。

2.Hermite 插值法的基本原理Hermite 插值法的基本思想是使用一个三次多项式来表示给定数据点之间的函数。

该多项式可以写成：f(x) = a0 + a1x + a2x^2 + a3x^3其中，a0、a1、a2 和 a3 是待定系数，需要通过给定的数据点来确定。

为了找到这些系数，Hermite 插值法使用了三个约束条件：（1）插值多项式在区间的端点处取到给定的函数值，即：f(x0) = a0 + a1x0 + a2x0^2 + a3x0^3 = y0f(x1) = a0 + a1x1 + a2x1^2 + a3x1^3 = y1（2）插值多项式在区间的中点处取到区间的平均值，即：f((x0 + x1) / 2) = (f(x0) + f(x1)) / 2（3）插值多项式的一阶导数在区间的中点处等于给定函数在该点的导数值，即：f"(((x0 + x1) / 2)) = (f"(x1) - f"(x0)) / (x1 - x0)通过解这组线性方程组，可以得到插值多项式的系数 a0、a1、a2 和a3。

一旦得到这些系数，就可以用插值多项式来近似表示给定函数在给定区间内的行为。

3.Hermite 插值法的应用实例Hermite 插值法广泛应用于数值分析、工程计算和计算机图形学等领域。

例如，在计算机图形学中，Hermite 插值法可以用来在给定控制点之间生成平滑的贝塞尔曲线。

实验二埃尔米特（Hermite）插值一、实验目的：1.掌握埃尔米特插值算法原理；2.使用C语言编程实现埃尔米特插值算法。

二、实验准备：阅读《数值分析》2.4节二、实验要求：某人从甲地开车去乙地，每隔一段时间对行车距离和速率进行一次采样，得到在n+1 个采样时刻点t i 的里程s i和速率v i（i=0, 1, ..., n）。

要求编程构造埃尔米特插值多项式H2n+1(t)，满足H2n+1(t i)=s i，H'2n+1(t i)=v i，对所有i=0, 1, ..., n成立，并据此计算m个给定时刻的里程和速率。

函数接口定义：void Hermite_Interpolation( int N, double t[], double s[], double v[], int m, double ht[], double hs[], double hv[] );其中N为采样点个数（注意这个N不是公式中的最大下标n，而是等于n+1），采样时刻点t i、里程s i、速率v i分别通过t、s、v传入；m是需要估算的给定时刻的个数，ht传入给定的时刻点，相应计算出的里程和速率应分别存储在hs和hv中。

裁判程序如下：裁判输入数据：20.0 1.00.0 1.00.0 0.050.0 0.2 0.5 0.8 1.030.0 0.5 1.0100.0 170.0 200.030.0 150.0 0.050.0 0.25 0.5 0.75 1.050.0 1.0 2.0 3.0 4.00.0 60.0 160.0 260.0 300.05.0 70.0 100.0 120.0 20.0100.5 1.0 1.5 2.0 2.5 3.0 3.5 3.8 3.95 4.0标准输出数据：0.0000 0.1040 0.5000 0.8960 1.00000.0000 0.9600 1.5000 0.9600 0.0000100.0000 127.9297 170.0000 195.9766 200.000030.0000 165.4688 150.0000 52.9688 0.000030.2222 60.0000 105.9303 160.0000 206.3438 260.0000 307.9764 305.7687 299.9796 300.000062.6024 70.0000 109.0488 100.0000 92.9745 120.0000 41.2374 -44.8421 -16.2783 20.0000#include<stdio.h>#define MAXN 5 /* 最大采样点个数 */#define MAXM 10 /* 最大估算点个数 */void Hermite_Interpolation( int N, double t[], double s[], double v[], int m, double ht[], double hs[], double hv[] ){double l[10],p[10],h1[10],h2[10],x,ll[10],pp[10];int kk;for(kk=0;kk<m;kk++){x=ht[kk];hs[kk]=0;hv[kk]=0;int i;for(i=0;i<N;i++){l[i]=1;ll[i]=1;int j;for(j=0;j<N;j++){if(i!=j){l[i]=l[i]*(x-t[j])/(t[i]-t[j]);}}p[i]=0;pp[i]=0;int k;for(k=0;k<N;k++){if(i!=k){p[i]=p[i]+l[i]/(x-t[k]);pp[i]=pp[i]+ll[i]/(t[i]-t[k]);}}h1[i]=(1-2*pp[i]*(x-t[i]))*l[i]*l[i];h2[i]=(x-t[i])*l[i]*l[i];hs[kk]=hs[kk]+s[i]*h1[i]+v[i]*h2[i];int kkk;for(kkk=0;kkk<N;kkk++){if(x==t[kkk])break;}if(x==t[kkk])hv[kk]=v[kkk];elsehv[kk]=hv[kk]+s[i]*(2*p[i]*l[i]-4*l[i]*p[i]*(x-t[i])*pp[i]-2*pp[i]*l[ i]*l[i])+v[i]*(l[i]*l[i]+2*l[i]*p[i]*(x-t[i]));}}}int main(){int N, m;double t[MAXN], s[MAXN], v[MAXN]; /* 用于构造的数据 */double ht[MAXM], hs[MAXM], hv[MAXM]; /* 用估算的数据 */int i;while ( scanf("%d", &N) != EOF ) {for ( i=0; i<N; i++ )scanf("%lf", &t[i]);for ( i=0; i<N; i++ )scanf("%lf", &s[i]);for ( i=0; i<N; i++ )scanf("%lf", &v[i]);scanf("%d", &m);for ( i=0; i<m; i++ )scanf("%lf", &ht[i]);Hermite_Interpolation( N, t, s, v, m, ht, hs, hv );for ( i=0; i<m; i++ )printf("%.4lf ", hs[i]);printf("\n");for ( i=0; i<m; i++ )printf("%.4lf ", hv[i]);printf("\n\n");}return 0; }。

基于降阶法的hermite插值多项式求解方法基于降阶法的Hermite插值多项式求解方法是一种数值分析方法，用于求解函数在给定点的值。

该方法的基本思想是将高阶多项式转化为低阶多项式，从而简化计算过程。

具体步骤如下：1. 定义插值点：选择一组已知的插值点 $(x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n)$，其中 $x_0 < x_1 < \ldots < x_n$。

2. 构造降阶多项式：对于 $i = 0, 1, \ldots, n$，定义 $p_i(x) = (x - x_i)\cdot q_i(x)$，其中 $q_i(x)$ 是 $(n-1)$ 阶多项式。

3. 求解 $q_i(x)$：对于 $i = 0, 1, \ldots, n$，求解 $(n-1)$ 阶方程$q_i(x_j) = \delta_{ij}$，其中 $\delta_{ij}$ 是 Kronecker delta 函数。

4. 求解 $p_i(x)$：对于 $i = 0, 1, \ldots, n$，求解 $(n+1)$ 阶方程$p_i(x_j) = y_j$。

5. 计算插值多项式：最终的插值多项式为 $H(x) = \sum_{i=0}^{n} p_i(x)\cdot \varphi_i(x)$，其中 $\varphi_i(x) = \frac{(x - x_0)(x - x_1) \cdots (x - x_{i-1})(x - x_{i+1}) \cdots (x - x_n)}{(x_i - x_0)(x_i - x_1) \cdots (x_i - x_{i-1})(x_i - x_{i+1}) \cdots (x_i - x_n)}$。

通过以上步骤，可以求解出满足给定插值条件的 Hermite 插值多项式。

在实际应用中，可以根据具体问题选择合适的插值点，并利用该方法进行数值计算。

实验四 Hermite 插值多项式1实习目的(1) 加深对Hermite 插值多项式的理解(2) 熟练掌握C 语言程序设计知识，熟练编写程序。

2班级：计算092，姓名:薛藏朋,学号：30908110723目的意义融会贯通Hermite 插值多项式，熟练编写有关程序，深化C 语言程序设计知识，培养坚韧的毅力。

4数学建模H i （x ）=+--+--1321))]((2[i i i i i y h x x x x h +--+-i ii i i y h x x x x h 321))]((2[ 221))((i i i h x x x x ---y '1-i +'221)()(i ii i y h x x x x --- 5算法Step1:'）,i=0,1,…,n;Step2:Step3:Step4:6（1（2）程序#include <stdio.h>#define N 50struct POINT /*定义一个点结构体*/{ double x;double y;double z;};void main(){int i,n;double x;struct POINT ps[N];/*定义一个点结构体的数组*/printf("please input n,0<=n<=50: \n");scanf("%d",&n);printf("please input xi,yi,yi'(z): \n");for(i=0;i<n;i++){ scanf("%lf,%lf,%lf",&ps[i].x,&ps[i].y,&ps[i].z);}printf("Now input x: \n");scanf("%lf",&x);/*输入差值x*/printf("please input i:\n");scanf("%d",&i);double hi,mi,ni,H;hi=ps[i].x-ps[i-1].x;mi=x-ps[i-1].x;ni=x-ps[i].x;H=(hi+2*mi)*ni*mi*ps[i-1].y/hi/hi/hi+(hi-2*ni)*mi*mi*ps[i].y/hi/hi/hi+mi*ni*ni*ps[i-1].z/hi/hi+mi*ni*ni*ps[i].z/hi/hi; printf("H%d(%lf)=%lf\n",i,x,H);}7数值算例8对计算结果进行分析评价实验结果在误差范围内，比较准确9参考文献【1】张毅坤，曹锰，张亚玲，C语言程序设计教程，西安交通大学出版社，2003. 【2】姚全珠，李薇，王晓帆，C++面向对象程序设计，北京：电子工业出版社，2010. 【3】秦新强，数值逼近，西安理工大学【4】王萼芳，石声明，高等代数，北京：高等教育出版社。

埃尔米特插值多项式简介埃尔米特插值多项式（Hermite Interpolation Polynomial）是一种常用的插值方法，用于通过给定的数据点集合来计算一个多项式，使得多项式在给定的数据点上与其函数值和导数值都完全匹配。

本文档将介绍埃尔米特插值多项式的原理、计算过程和应用。

基本原理埃尔米特插值多项式的基本思想是通过插值条件来求解多项式的系数。

给定数据点集合和对应的函数值和导数值，目标是找到一个多项式，使得多项式在给定的数据点上与其函数值和导数值都完全匹配。

首先，对于每一个给定的数据点，我们需要求解一个插值多项式。

插值多项式的次数应该比给定数据点的个数少 1。

例如，给定数据点集合{ (x0, f0, f'0), (x1, f1, f'1), ... , (xn, fn, f'n) }，我们需要找到一个次数为n的多项式H(x)。

对于每一个数据点(xi, fi, f'i)，插值多项式H(x)满足以下条件：1.H(xi) = fi，即多项式在数据点上与函数值完全匹配2.H'(xi) = f'i，即多项式在数据点上与导数值完全匹配根据这两个条件，我们可以构建一个n+1次的多项式，满足上述条件。

计算过程下面是埃尔米特插值多项式的计算过程：1.根据给定的数据点集合，构建一个空的多项式，初始阶次为 0，即H(x) = a02.对于每一个数据点(xi, fi, f'i)：–计算多项式的阶次n，并更新多项式的阶次为n+1–求解f'i的差商f'i / (xi - x0)，记为f'i / (x[i]-x0)–更新多项式的系数a，使得H(x) = H(x) + a * (x - x0)^i–更新多项式H(x)的阶次为n3.返回多项式H(x)应用埃尔米特插值多项式在实际应用中具有广泛的用途，包括但不限于以下领域：1.数值计算和近似：埃尔米特插值多项式可以用于通过已知的函数值和导数值来近似计算未知的函数值，用于求解数值问题。

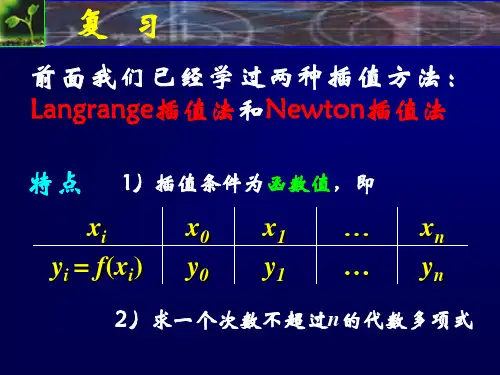
数值分析常用的插值方法数值分析中常用的插值方法有线性插值、拉格朗日插值、分段线性插值、Newton插值、Hermite插值、样条插值等。

下面将对这些插值方法进行详细介绍。

一、线性插值（linear interpolation）线性插值是最简单的插值方法之一、假设已知函数在两个点上的函数值，通过这两个点之间的直线来估计中间点的函数值。

线性插值公式为：f(x)=f(x0)+(x-x0)*(f(x1)-f(x0))/(x1-x0)其中，f(x)表示要求的插值点的函数值，f(x0)和f(x1)是已知的两个点上的函数值，x0和x1是已知的两个点的横坐标。

二、拉格朗日插值（Lagrange interpolation）拉格朗日插值是一种基于多项式的插值方法。

它通过多个已知点的函数值构造一个多项式，并利用这个多项式来估计其他点的函数值。

拉格朗日插值多项式的一般形式为：f(x) = Σ[f(xi) * Li(x)] (i=0,1,2,...,n)其中，f(x)表示要求的插值点的函数值，f(xi)是已知的多个点的函数值，Li(x)是拉格朗日基函数。

拉格朗日基函数的表达式为：Li(x) = Π[(x-xj)/(xi-xj)] (i≠j，i,j=0,1,2,...,n)三、分段线性插值（piecewise linear interpolation）分段线性插值是一种逐段线性近似函数的方法。

通过将整个插值区间分成多个小段，在每个小段上使用线性插值来估计函数的值。

分段线性插值的过程分为两步：首先确定要插值的点所在的小段，在小段上进行线性插值来估计函数值。

四、Newton插值（Newton interpolation）Newton插值也是一种基于多项式的插值方法。

利用差商的概念来构造插值多项式。

Newton插值多项式的一般形式为：f(x)=f(x0)+(x-x0)*f[x0,x1]+(x-x0)*(x-x1)*f[x0,x1,x2]+...其中，f(x)表示要求的插值点的函数值，f(x0)是已知的一个点的函数值，f[xi,xi+1,...,xi+k]是k阶差商。

构造二元四次Hermite插值公式的方法崔利宏;高小淞;孟敏;李笑笑【摘要】本文以文献[1]中给出构造二元Hermite插值多项式的方法为基础,给出了以迭加插值方式构造二元四次不缺项Hermite插值多项式的方法,并且给出实例验证了所构造出的Hermite插值多项式的逼近有效性和确定性.【期刊名称】《吉林师范大学学报（自然科学版）》【年(卷),期】2015(036)001【总页数】3页(P63-65)【关键词】二元Hermite插值;迭加插值法;插值条件【作者】崔利宏;高小淞;孟敏;李笑笑【作者单位】辽宁师范大学数学学院,辽宁大连116029;辽宁师范大学数学学院,辽宁大连116029;辽宁师范大学数学学院,辽宁大连116029;辽宁师范大学数学学院,辽宁大连116029【正文语种】中文【中图分类】O174.410 引言文献[2,3]中给出了如下二元Hermite插值问题的定义:设P1(x,y),P2(x,y),… ,PM(x,y)是M个线性独立的二元多项式函数，它们所张成的实系数线性空间记为H．人们通常所研究的二元Hermite插值问题，就是要构造出多项式函数P(x,y)∈H，使之满足如下条件：(1)对一切(k,l)∈Ii，i=1，2，…,n成立，其中是事先任意给定的一组实数，(xi，yi)(i=1,2,…,n)是欧氏平面上互不相同的n个点，Ii表示欧氏平面上有限个非负整数点所构成的集合，Dikl称之为插值泛函算子，而集合E={Dikl|(k,l)∈Ii，i=1，2，…,n}称之为插值泛函算子组．凡是满足条件(1)的多项式函数P(x,y)称为Hermite插值多项式函数．当插值多项式空间H和插值泛函算子组E都同时给定时，P(x,y)就仅仅依赖于数组fikl．如果对任意给定的数组fikl，如此的多项式函数P(x,y)∈H总是存在而且唯一，则称E是H的正则Hermite插值泛函算子组，H 是E的正则Hermite插值多项式空间，并且称这种Hermite插值问题为正则Hermite插值问题．实际科研生产中，由已知数组fikl来求得插值多项式P(x,y)的最简单方法就是利用Hermite插值公式．本文就是在文献[1]中所提到的构造二元Hermite插值公式的方法——迭加插值法的基础上，给出了构造二元四次不缺项Hermite插值多项式的插值格式方法．1 迭加Hermite插值方法所谓迭加Hermite插值方法就是给定了m个二元多项式空间Q1，Q2…，Qm和m个Hermite插值泛函算子组H1，H2，…，Hm，使其满足如下两个条件：A.Hi是Ei的适定空间；B．当P(x,y)∈Qi时，对一切都有DP(x,y)=0；若用P1，P2，…,Pm分别表示Q1,Q2，…,Qm中的多项式函数一般表达式，则实现该Hermite插值算法就是利用被插值函数在H1,H2，…,Hm作用下的值来依次定出表达式P(x,y)=P1(x,y)+P2(x,y)+…+Pm(x,y)中的P1,P2，…,Pm，而这样所得到的多项式P(x,y)就是所要求得的Hermite插值多项式．在文献[1]中已证得，任何一个正则Hermite插值问题原则上都可以通过迭加Hermite插值法来实现．2 用迭加插值法构造的一些二元Hermite插值格式在上面我们提到的迭加Hermite插值法的一个特殊功能就是用来解决n次不缺项的二元多项式的Hermite插值问题，其具体方法如下：在二维欧氏平面上任意做m+1条垂直直线x=xk，k=0，1，… m,在x=x0上取m+1个相异点，在x=x2上取m个相异点，…，在x=xm上取一个点；在每一条直线上所取的点中有且仅有一个点要求0到r阶偏微商(也就是关于x,y的混合微商次数不超过r的Hermite条件数(共个条件)，而在其余点处要求关于x和关于y 都是0到r阶偏微商的Hermite条件数(共有(r+1)2个条件)．现在要求构造一个n=(m+1)r+m次二元Hermite插值多项式P(x,y)满足这些插值条件．根据迭加Hermite插值法，我们只需考虑如下形式的多项式P(x,y)即可，其中Pij(y)是y的(m+1)r-i(r+1)-j+m次多项式的一般形式．由文献[2]可以得出，形如的多项式所张成出的空间是直线x=xi上插值条件的正则Hermite插值空间．为确定出P(x,y)，我们只须根据直线x=x0，x=x1,…,x=xm上的Hermite插值条件依次定出P0j(y)，P1j(y)，…，Pmj(y)的系数即可．2.1 直角三角形上的二元四次Hermite插值多项式运用上述方法，下面我们来构造在直角三角形区域上的二元四次不缺项的Hermite插值格式，并举例说明所构造出来的Hermite插值格式的有效性．在平面上取两条垂直直线x=0，x=1，并在直线x=0上取两个点(0,0)和(0,1)，在x=1上取一个点(1，0)，容易看出这三个点两两连线后就围成一个直角三角形，则这个直角三角形的三个顶点即为插值结点．令(x0,y0)=(0，0)，(x1,y0)=(1，0)，(x0,y1)=(1，0)，要求构造一个二元四次多项式P(x,y)，使之满足如下条件：根据所提出的算法知：一定存在一个不缺项的二元四次多项式P(x,y)= a0+a1y+a2y(y-1)+a3[y(y-1)]2+x{a4+a5y+a6y(y-1)2}+x2{a7+a8(x-1)2+a9y(y-1)+a10xy}经计算可得到：a0=f(0,0)a1=f(0,1)-f(0,0)计算实验：使用文献[3,4,5] 中所给方法，取f(x,y)=ex+y，要求近似计算出的值．利用上述插值格式构造方法可以求出而其相对误差为0.0408．2.2 直角三角形上的二元三次Hermite插值多项式我们仍在上面所给出的三角形域上考虑问题．现在欲求一个三次多项式P(x,y)，使之满足如下Hermite插值条件：根据所提出的算法，我们知道一定存在一个不缺项的二元三次多项式P(x,y)= a0+a1y+a2y(y-1)+a3y2(y-1)+x{a4+a5y+a6y(y-1)}+x2{a7+a8(x-1)+a9y}满足我们的要求．多项式的系数经过计算便可求出：a0=f(0,0),a1=[0|10],a2=[0|10]-(0,0),a3=[0|10]y-2{[0|10]+(0，0)}a4=(0,0),a5=[0|10]x,a6=(0，1)-(0,0)-(0,0),a7=[10|0]-(0,0)其中计算实验：使用文献[3,4，5] 中所给方法，取f(x,y)=ex+y，要求近似计算出的值．利用上述公式可以求出而其绝对误差为0.0423，相对误差为0.035．通过上述两个例子和相应的计算实验可以看出，利用迭加Hermite插值法构造出的不缺项的二元多项式Hermite插值公式的确定性和准确性．参考文献【相关文献】[1]梁学章，朱功勤．构造二元切触插值公式的方法[J]．数学研究与评论，1981，(1)：91～100．[2]梁学章．二元插值的适定结点组与迭加插值法[J]．吉林大学学报(自然科学版),1979,(1)：27～32.[3]梁学章,李强.多元逼近[M].北京:国防工业出版社,2005.[4]崔利宏,王攀，徐永辉.关于多元分次插值唯一可解问题的研究[J]．吉林师范大学学报(自然科学版)，2010，31(3)：4～8．[5]崔利宏，李跃玲．二元分次插值适定结点组的新的构造方法[J]．吉林师范大学学报(自然科学版)，2009，30(1)：1～2．[6]梁学章.二元四次样条插值与有限元法[J].吉林大学学报(自然科学版)，1978，(01)：85～95．[7]A.C.Ahlin.A bivariate generalization of Hermite’s in terpolation formula[J]p.，1964,18:264～273．[8]崔利宏,张志辉,李纬国.关于二元Hermite插值问题的某些研究[J].辽宁师范大学学报(自然科学版)，2012，29(02)：264～266．[9]徐利治,王仁宏,周蕴时.边界型求积公式的构造方法及应用[J].计算数学，1978,(03)：54～75．[10]李庆扬等编.数值分析[M].武汉：华中理工大学出版社,1986．[11]谢赞福.插值函数的一种构造方法[J].广东民族学院学报(自然科学版)，1989，(04)：59～65．[12]朱平.关于多元多项式插值的一点注记[J].中山大学学报论丛，1996，(5)：140～141．。

Hermite-Fejér插值多项式的逼近阶的报告，600字Hermite-Fejér插值是一种多项式逼近法，也被称为双重插值法。

它通过使用特征的函数和其他函数的交叉来提供令人满意的精度比仅使用函数要高得多。

它的工作原理与Lagrange和Newton插值法相似，但它的函数是特征的，而不是分片的。

Hermite-Fejér插值的术语“逼近阶”用于描述所需的函数数量。

总而言之，逼近阶数是指用于拟合原始数据点的函数的数量。

更高的逼近阶可能更准确地拟合原始数据，但也可能出现更多的误差。

Hermite-Fejér插值多项式逼近阶的大小决定了多项式函数的复杂性。

具体而言，随着逼近阶的增加，多项式的复杂度也会增加。

为了获得更准确的拟合，必须按照适当的步骤增加逼近阶。

为了计算Hermite-Fejér插值多项式的逼近阶，首先需要计算原始数据集中每个数据点的导数矩阵。

然后，要选择一系列特征函数，将其相乘，并使用多项式拟合方法将其拟合到原始数据点。

最后，计算所需的多项式函数数量，就是逼近阶。

计算Hermite-Fejér插值多项式的逼近阶需要大量的数学知识，涉及多项式拟合方法、特征的曲线和多元函数拟合。

通常，一个熟练的工程师可以通过多次尝试并使用特别的计算机程序来估计逼近阶。

此外，计算Hermite-Fejér插值多项式的逼近阶还可以通过使用特殊的公式来简化过程。

一旦完成计算，工程师可以使用所得多项式来拟合原始数据点，以获得更准确和精确的结果。

总而言之，Hermite-Fejér插值多项式逼近阶是用于拟合原始数据点的多项式函数的数量，也决定了多项式的复杂度。

其计算可以通过使用特殊公式或多次尝试来完成，而且经过适当调整，可以得到更准确和精确的结果。

两点三次hermite插值例题Hermite插值是一种数值分析方法，用于在给定的数据点上生成一个多项式函数，以便通过这些数据点来近似描述一个函数。

Hermite插值是利用函数值和导数值来进行插值的一种方法，它可以更精确地逼近给定的数据点。

下面我将通过一个例题来说明Hermite插值的过程。

假设我们有以下数据点，(1, 2), (1, 3), (2, 1), (2, 2)，我们要使用Hermite插值来找到通过这些点的多项式函数。

首先，我们需要计算每个数据点的导数值。

因为数据点中有重复的x值，我们需要分别计算每个x值对应的导数值。

对于数据点(1, 2)和(1, 3)，我们可以假设它们对应的导数值分别为2和3；对于数据点(2, 1)和(2, 2)，我们可以假设它们对应的导数值分别为1和2。

接下来，我们将使用这些数据点和导数值来构建Hermite插值多项式。

Hermite插值多项式的一般形式为：\[P(x) = \sum_{i=0}^{n}f[x_0, x_1, \ldots, x_i](x-x_0)(x-x_1)\ldots(x-x_{i-1}) + \sum_{i=0}^{n}f[x_0, x_1,\ldots, x_i, x_i](x-x_0)(x-x_1)\ldots(x-x_{i-1})^2\]其中，\[f[x_0, x_1, \ldots, x_i]\]表示数据点\[x_0, x_1, \ldots, x_i\]处的插值函数值。

这个式子的第一部分表示通过数据点的函数值进行插值，第二部分表示通过数据点的导数值进行插值。

我们可以根据给定的数据点和导数值，计算出Hermite插值多项式。

最终得到的多项式函数就是通过这些数据点进行Hermite插值得到的结果。

总结起来，Hermite插值是一种利用函数值和导数值进行插值的方法，可以更精确地逼近给定的数据点。

通过计算数据点的导数值和使用Hermite插值多项式的公式，我们可以得到一个通过这些数据点的多项式函数。