Hermite插值法
- 格式:ppt
- 大小:673.00 KB
- 文档页数:16


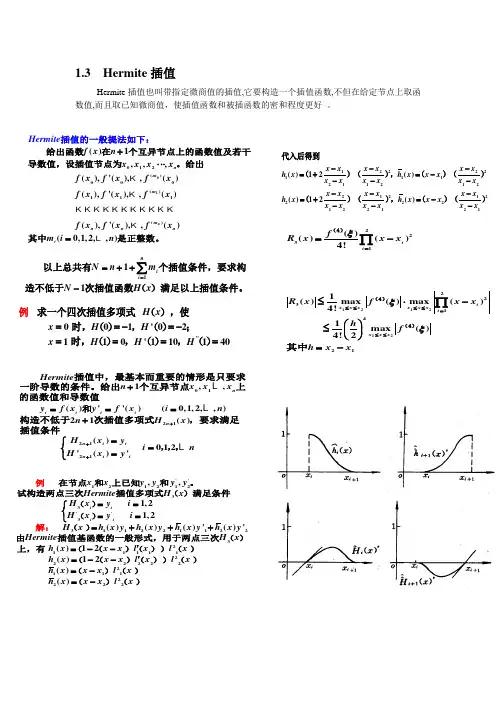
1.3 Hermite 插值Hermite 插值也叫带指定微商值的插值,它要构造一个插值函数,不但在给定节点上取函数值,而且取已知微商值,使插值函数和被插函数的密和程度更好 。
01012()000()111()()1,,,(),'(),,()(),'(),,()(),'(),,()(0,1,2,,)n n m m m n n ni H f x n x x x x f x f x f x f x erm f x f x f x f x it f x m i n e +⋅⋅⋅=插值的一般提法如下给出函数在个互异节点上的函数值及若干导数值,设插值节点为。
给出其中是:正整数。
111ni i N n m N H x ==++-∑以上总共有个插值条件,要求构造不低于次插值函数()满足以上插值条件。
''001'02110'110140H x x H H x H H H ==-=-====求一个四次插值多项式(),使 时,(),(); 时,(),(),()例012121211,,()''()(0,1,2,,)21()()012'()'n i i i i n n i in ii Hermite n x x x y f x y f x i n n H x H x y i n H x y ++++===+=⎧=⎨=⎩插值中,最基本而重要的情形是只要求一阶导数的条件。
给出个互异节点上的函数值和导数值和构造不低于次插值多项式,要求满足插值条件,,,''12121233''331122112232111112,,1,21,2()()()'()'()12()1i i i i x x y y y y Hermite H x H x y i H x y i H x h x y h x y h x y h x y Hermite H x h x x x l x l x h x ==⎧⎨==⎩=+++'=--=-在节点和上已知和。








Hermite插值法是解决数学建模中预测类问题的最常用的方法,可以有效的解决“已知数据”数量不够的问题。
但是,直接使用Hermite插值得到的多项式次数较高,也存在着“龙格现象(Runge phenomenon)”。
因此,在实际应用中,往往使用分段三次Hermite插值多项式(PCHIP),来提高“模拟数据的准确性”。
Hermite插值法运用及原理:
1.Hermite插值法的含义是保持插值曲线在节点处有切线(光滑),使得插
值函数和被插值函数的密合程度更好。
2.Hermite插值不但要求在节点处上的函数值相等,而且还要求对应的导数
值也相等,甚至要求高阶导数也相等。
3.满足这种要求的插值多项式就是“Hermite插值多项式”。
Hermite插值法是一种用于构造多项式插值函数的方法,它可以通过给定的数据点和导数值来构造一个满足这些条件的插值多项式。
Hermite插值法的原理可以分为以下几个步骤:
1. 给定一组数据点和对应的函数值,以及这些数据点处的导数值。
2. 构造一个基函数集合,这些基函数是一组满足插值条件的函数。
常用的基函数是Hermite基函数,它是一组多项式函数。
3. 根据给定的数据点和导数值,利用基函数集合构造插值多项式。
这可以通过求解一个线性方程组来实现,其中方程组的未知数是插值多项式的系数。
4. 得到插值多项式后,可以使用它来估计在其他点上的函数值。
Hermite插值法的优点是可以通过给定的导数值来更好地逼近原函数的特性,尤其在数据点附近的插值效果更好。
然而,
它的缺点是在数据点之间的插值效果可能不够理想,因为它只是通过给定的数据点和导数值来构造插值多项式,而没有考虑其他可能的信息。