向量的线性运算

第24章 第四节 平面向量的线性运算§24.7向量的线性运算 教学目标(1)知道向量的线性运算的意义，会化简线性运算的算式，会画图表示简单的线性运算结果.(2)知道向量的线性组合，会在较熟悉的几何图形中将一个向量用两个给定的不平行向量的线性组合表示。

(3)知道向量的分解式，能画出平面内一个向量在已知两个不平行向量方向上的分向量。

(4)在知识形成和运用过程中，体会向量的线性组合与分解的辩证关系，体会数形结合、化归等数学思想方法。

教学重点让学生理解向量的线性运算的含义，知道向量的线性组合。

引进向量的分解式，帮助学生学会画平面内一个向量在已知两个不平行向量方向上的分向量。

知识精要1.向量加法、减法、实数与向量相乘以及它们的混合运算叫做向量的线性运算。

2.如果a b 、是两个不平行的向量，x y 、是实数，那么xa yb +叫做a b 、的线性组合。

3.如果a b 、是两个平行的向量，c ma nb =+(m n 、是实数)，那么向量c 就是向量ma 与nb 的合成。

用a b 、的线性组合表示向量c ，也可以说是对向量c 分解。

这时，向量ma 与nb 是向量c 分别在a b 、方向上的分向量，ma nb +是向量c 关于a b 、的分解式。

4.平面上任意一个向量都可以在给定的两个不平行向量的方向上分解。

用作图的方法，可以作出这个向量在给定的两个不平行向量的方向上的分向量。

经典题型解析(一)向量的线性组合例1.如右图，已知两个不平行的非零向量a b 、，求作满足 关系式3(3)2(4)a x b x -=-的向量x 。

a b随堂练习：如图，已知两个不平行的向量a 、b ，求作：3()(3)2a b a b ---。

b a例2.(1)已知在ABC ∆中，点D E 、分别在边AB AC 、上，//DE BC ，且2AD DB =。

若AB a =，AC b =，则向量DE 可用a b 、表示为___________。

空间向量的线性运算空间向量是三维空间中的一个重要概念，它具有方向和大小。

在现实生活和科学研究中，我们常常需要对空间向量进行各种数学操作和运算。

本文将介绍空间向量的线性运算，包括向量的加法、减法、数量乘法以及与数的乘法。

1. 向量的加法向量的加法是指将两个向量相加得到一个新的向量。

设有两个向量A和B，它们的坐标分别表示为(Ax, Ay, Az)和(Bx, By, Bz)。

则两个向量的加法运算可以表示为：A +B = (Ax + Bx, Ay + By, Az + Bz)2. 向量的减法向量的减法是指将两个向量相减得到一个新的向量。

设有两个向量A和B，它们的坐标分别表示为(Ax, Ay, Az)和(Bx, By, Bz)。

则两个向量的减法运算可以表示为：A -B = (Ax - Bx, Ay - By, Az - Bz)3. 数量乘法数量乘法是指将一个向量与一个标量相乘得到一个新的向量。

设有一个向量A和一个标量k，向量A的坐标表示为(Ax, Ay, Az)。

则向量A与标量k的数量乘法运算可以表示为：kA = (kAx, kAy, kAz)4. 向量与数的乘法向量与数的乘法是指将一个向量的每个分量都与一个相同的数相乘得到一个新的向量。

设有一个向量A和一个数k，向量A的坐标表示为(Ax, Ay, Az)。

则向量A与数k的乘法运算可以表示为：A * k = (Ax * k, Ay * k, Az * k)空间向量的线性运算具有以下几个重要性质：1. 加法交换律对于任意的向量A和B，有A + B = B + A。

2. 加法结合律对于任意的向量A、B和C，有(A + B) + C = A + (B + C)。

3. 减法与加法的关系向量减法可以看作是加法的逆运算，即A - B = A + (-B)，其中-A表示向量B取相反数得到的向量。

4. 标量乘法分配律对于任意的向量A和标量k、m，有k(A + B) = kA + kB，(k + m)A = kA + mA。

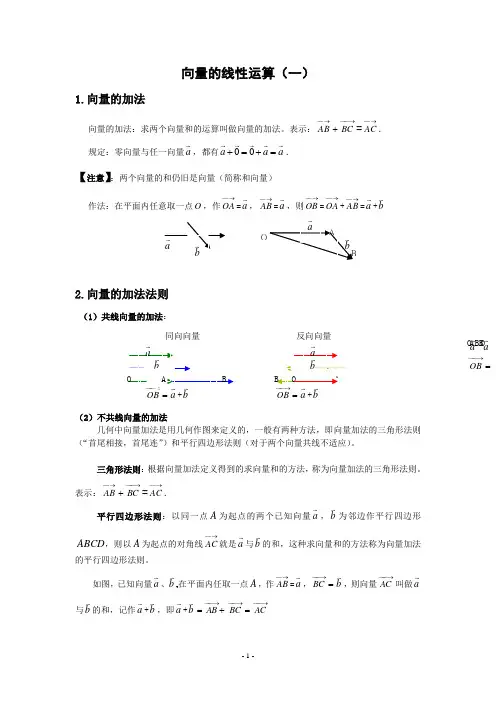
ABabbaa a O =−→−OBA B O B a abb=−→−OB a +b ABAa +b向量的线性运算（一）1.向量的加法向量的加法：求两个向量和的运算叫做向量的加法。

表示：→--AB −→−+BC =→--AC ．规定：零向量与任一向量a ，都有00a a a +=+=．【注意】：两个向量的和仍旧是向量（简称和向量）作法：在平面内任意取一点O ，作→--OA =a →--→--OB =→--OA +→--AB a +b2.向量的加法法则（1）共线向量的加法：同向向量反向向量（2）不共线向量的加法几何中向量加法是用几何作图来定义的，一般有两种方法，即向量加法的三角形法则（“首尾相接，首尾连”）和平行四边形法则（对于两个向量共线不适应）。

三角形法则：根据向量加法定义得到的求向量和的方法，称为向量加法的三角形法则。

表示：→--AB −→−+BC=→--AC ．平行四边形法则：以同一点A 为起点的两个已知向量a ，b 为邻边作平行四边形ABCD ，则以A 为起点的对角线→--AC 就是a 与b 的和，这种求向量和的方法称为向量加法的平行四边形法则。

如图，已知向量a 、b 在平面内任取一点A ，作→--AB =a ，=−→−BC b ，则向量−→−AC 叫做a与b 的和，记作a +b ，即a +b +=−→−AB =−→−BC −→−AC【说明】：教材中采用了三角形法则来定义，这种定义，对两向量共线时同样适用，当向量不共线时，向量加法的三角形法则和平行四边形法则是一致的 特殊情况：探究：（1）两相向量的和仍是一个向量；（2）当向量a 与b 不共线时，a +b 的方向不同向，且|a +b |<|a |+|b |; （3）当a 与b 同向时，则a +b 、a 、b 同向，且|a +b |=|a |+|b |,当a 与b 反向时，若|a |>|b |,则a +b 的方向与a 相同，且|a +b |=|a |-|b |；若|a |<|b |,则a +b 的方向与b 相同，且|a +b |=|b |-|a |.（4）“向量平移”：使前一个向量的终点为后一个向量的起点，可以推广到n 个向量连加3.向量加法的运算律（1）向量加法的交换律：a +b =b +a（2）向量加法的结合律：(a +b ) +c =a +(b +c ) 证明：如图：使=−→−AB a , =−→−BC b , =−→−CD c 则(a +b )+c =−→−AC +=−→−CD −→−AD ，a + (b +c )=−→−AB −→−+BD −→−=AD ,∴(a +b )+c =a +(b +c )从而，多个向量的加法运算可以按照任意的次序、任意的组合来进行例如：()()()()a b c d b d a c +++=+++；[()]()a b c d e d a c b e ++++=++++．例题：例1. O 为正六边形的中心，作出下列向量：（1）−→−OA +−→−OC （2）−→−BC +−→−FE （3）−→−OA +−→−FE例2．如图，一艘船从A 点出发以h km /32的速度向垂直于对岸的方向行驶，同时水aaab bba +ba +b ABC ABCD三角形法则平行四边形法则的流速为h km /2，求船实际航行的速度的大小与方向。

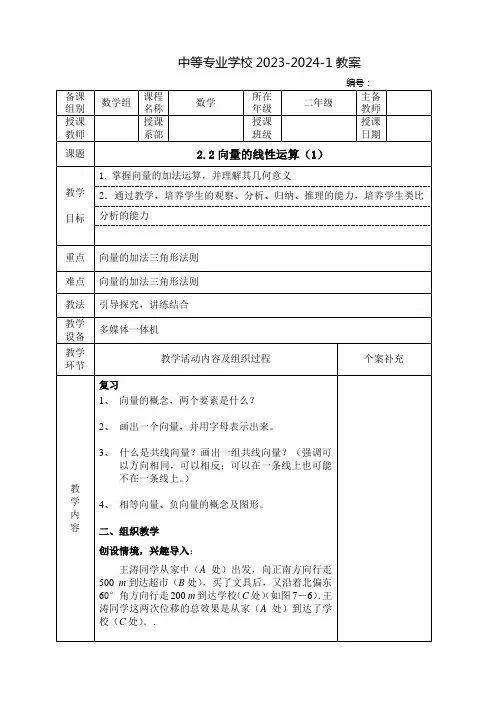
中等专业学校2023-2024-1教案AC 叫做AB 与位BC 的和AC =AB +BC ．AB =a , BC =b ，则向量AC 叫做，记作a ＋b ，即 AB ＋BC =AC 求向量的和的运算叫做向量的加法．上述求向量的和的方法叫做向量加法的三角形法则．可以看到：依照三角形法则进行向量的加法运算，运算的结果仍然是向量，叫做Aaab中等专业学校2023-2024-1教案AD=BC，AB＋AD=AB＋BC=ACD CAC所表示的向AB与AD的和．这种求和方法叫做向量加法的平行四边形法则．平行四边形法则不适用于共线向量，AB表示船速，AC为水流速度，由向量加法的平行四边形法则，AD是船的实际行速度，22=+=22AD AB AC+125中等专业学校2023-2024-1教案+++=AB BC CD DE AE：判断下列各等式是否正确：AB BC CD DA ++=二．向量的减法：与a 长度相等，方向相反的向量，叫做-(-a)=a ， ,a b ，如果a 是b 与另一个向量x 相加 ，即b x a +=；那么怎样求出x ?由作图得出：图b BC a +=；即：a b BC -=；图3：()a b AC +-=；即：a b AC -=. 向量的减法：在平面内取一点，以这个点为公共起点作出这两个向量，那么它们的差向量是以减向量的终点为起点，被减向量的终点为终点的向量. CBAbaa-b图1图2,,AB AD AC 表,BD DC,,a b c ；求作：a b c -+ a b c --提示：可以用减去一个向量等于加上这个向量 的相反向量来考虑作图D B A中等专业学校2023-2024-1教案。

向量线性运算知识点总结一、向量的定义在数学中，向量通常用箭头符号表示，比如$\vec{a}$或者$\overrightarrow{AB}$。

向量是有方向和大小的量，通常用于表示空间中的位移、速度等。

在n维空间中，一个向量可以表示为一个具有n个有序实数的n维坐标组$(x_1, x_2, \cdots, x_n)$，而在实际应用中，可以用行向量或列向量来表示。

在数学中，向量可以用于表示空间几何中的位移、速度、力等，同时也可以用于表示抽象意义上的量，比如代数中的多项式、矩阵等。

在计算机科学中，向量也被广泛应用于向量空间的表示，比如在机器学习中的特征向量等。

二、向量的线性运算向量的线性运算包括两种基本运算：向量的加法和数乘运算。

1. 向量的加法设有两个n维向量$\vec{a}=(a_1,a_2,\cdots,a_n)$和$\vec{b}=(b_1,b_2,\cdots,b_n)$，则它们的和是一个n维向量，记作$\vec{a}+\vec{b}=(a_1+b_1,a_2+b_2,\cdots,a_n+b_n)$。

向量的加法满足以下性质：- 交换律：$\vec{a}+\vec{b}=\vec{b}+\vec{a}$- 结合律：$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$- 零向量：对于任意向量$\vec{a}$，都有$\vec{a}+\vec{0}=\vec{a}$，其中$\vec{0}$表示零向量- 相反向量：对于任意向量$\vec{a}$，都有$\vec{a}+(-\vec{a})=\vec{0}$，其中$-\vec{a}$表示向量$\vec{a}$的相反向量2. 数乘运算设有一个n维向量$\vec{a}=(a_1,a_2,\cdots,a_n)$和一个实数$k$，则它们的数乘运算结果是一个n维向量，记作$k\vec{a}=(ka_1,ka_2,\cdots,ka_n)$。

《24.7向量的线性运算》讲义同学们好，咱们现在已经到了九年级啦，在沪教版（上海）的数学教材里，今天咱们要一起学习第二十四章相似三角形里的第四节内容，也就是向量的线性运算。

这部分知识呀，就像打开数学世界里一个新的小宝藏箱，里面有很多有趣的东西等着咱们去发现呢。

那什么是向量呢？我给大家讲个事儿啊。

有一次我去公园遛弯儿，看到一个小朋友在放风筝。

那风筝线就好像是一个向量。

风筝线有长度吧，这就相当于向量的大小；风筝线还有方向，是朝着天上风筝的方向，这就是向量的方向。

所以说向量这个东西啊，就是既有大小又有方向的量。

咱们再来说说向量的表示方法。

通常呢，我们可以用有向线段来表示向量。

就像刚刚说的风筝线，我们可以把它看成是一条有方向的线段。

在纸上画的时候，我们用一个箭头来表示方向，线段的长度就表示向量的大小。

比如说，我们画一个小箭头从点A指向点B，这个就可以表示一个向量，我们可以写成向量AB，这个箭头可不能丢哦，丢了就不知道方向啦。

一、向量的加法运算1、三角形法则咱们先来讲向量加法的三角形法则。

还是拿刚刚放风筝的事儿来说，假如这个小朋友先往东走了一段距离，这可以看成是一个向量，我们就叫向量a吧。

然后呢，他又往北走了一段距离，这就是另一个向量，叫向量b。

那他从最开始的位置到最后的位置这个总的位移呢，就是向量a和向量b的和。

咱们在图上画的时候，就把向量a的终点和向量b的起点连起来，然后从向量a的起点指向向量b的终点的这个向量，就是向量a加向量b。

这就像你要去一个地方，先走了一段路，接着又走了另一段路，总的路程就是这两段路的合成。

2、平行四边形法则除了三角形法则，向量加法还有平行四边形法则呢。

想象一下，你和你的小伙伴一起推一个箱子。

你从箱子的左边往右边用力，这是一个向量，你的小伙伴从箱子的前面往后面用力，这是另一个向量。

那箱子最终移动的方向和距离呢，就是这两个向量的和。

在图上怎么画呢？我们把这两个向量的起点放在一起，然后以这两个向量为邻边作一个平行四边形，那从这两个向量共同的起点指向平行四边形对角顶点的这个向量，就是这两个向量的和。

空间向量的线性运算与应用在线性代数中，空间向量的线性运算是一种常见的运算方式，它涉及向量的加法、减法、数乘、内积和投影等操作。

这些运算不仅在理论上有重要意义，而且在实际应用中也发挥着重要作用。

本文将介绍空间向量的线性运算及其应用。

一、向量的加法向量的加法是指将两个向量进行对应分量的相加。

设有两个向量a=[a₁,a₂,a₃]和a=[a₁,a₂,a₃]，则它们的和记作a+a，即：a+a=[a₁+a₁, a₂+a₂, a₃+a₃]向量的加法满足交换律和结合律，即a+a=a+a和(a+a)+a=a+(a+a)。

向量的加法应用广泛，例如在力学中，我们可以利用向量的加法来求解多个力的合力，进而研究物体的平衡和运动状态。

二、向量的减法向量的减法是指将两个向量进行对应分量的相减。

设有两个向量a=[a₁,a₂,a₃]和a=[a₁,a₂,a₃]，则它们的差记作a-a，即：a-a=[a₁-a₁, a₂-a₂, a₃-a₃]向量的减法和向量的加法类似，满足交换律和结合律。

向量的减法可以用于求解两个物体之间的位移或距离等问题。

三、向量的数乘向量的数乘是指将一个标量与一个向量的每个分量分别相乘，得到一个新的向量。

设有一个向量a=[a₁,a₂,a₃]和一个实数k，它们的数乘记作k a，即：k a=[k a₁, k a₂, k a₃]向量的数乘满足分配律，即k(a+a)=k a+k a。

向量的数乘可以改变向量的大小和方向，在几何上有重要应用。

四、向量的内积向量的内积又称为点积，是指将两个向量的对应分量相乘后相加所得到的一个标量。

设有两个向量a=[a₁,a₂,a₃]和a=[a₁,a₂,a₃]，则它们的内积记作a·a，即：a·a=a₁a₁+a₂a₂+a₃a₃向量的内积有一些重要的性质，如a·a=a·a（交换律）和a·(a+a)=a·a+a·a（分配律）等。

向量的内积可以用于计算夹角、判断两个向量的正交性以及求解投影等问题。