2008年数学中考试题分类汇编(解直角三角形)

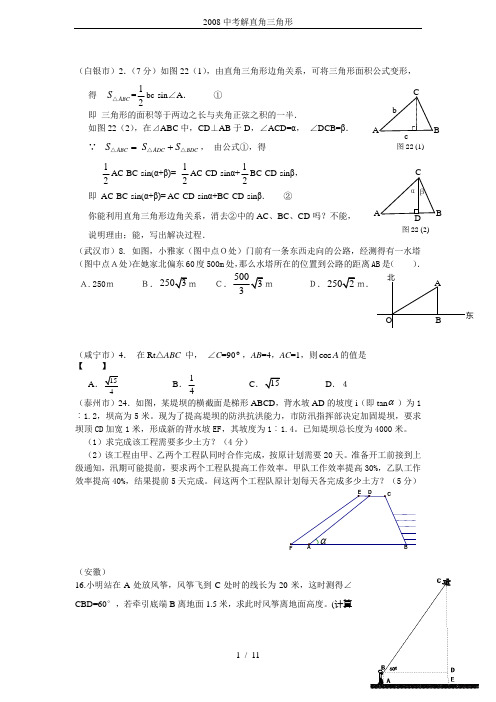
（白银市）2．（7分）如图22（1），由直角三角形边角关系，可将三角形面积公式变形， 得 ABC S △=12bc·sin ∠A ． ① 即 三角形的面积等于两边之长与夹角正弦之积的一半． 如图22（2），在⊿ABC 中，CD ⊥AB 于D ，∠ACD=α， ∠DCB=β． ∵ ABC ADC BDC S S S =+△△△， 由公式①，得12AC·BC·sin(α+β)= 12AC·CD·sin α+12BC·CD·sin β， 即 AC·BC·sin(α+β)= AC·CD·sin α+BC·CD·sin β． ②你能利用直角三角形边角关系，消去②中的AC 、BC 、CD 吗？不能， 说明理由；能，写出解决过程．（武汉市）8. 如图，小雅家（图中点Ｏ处）门前有一条东西走向的公路，经测得有一水塔（图中点Ａ处）在她家北偏东60度500m 处，那么水塔所在的位置到公路的距离AB 是（ ）． Ａ.250ｍＢ．Ｄ．（咸宁市）4．在Rt △ABC 中， ∠C =90︒，AB =4，AC =1，则cos A 的值是【 】A B ．14C D ．４（泰州市）24．如图，某堤坝的横截面是梯形ABCD ，背水坡AD 的坡度i （即tan α）为1︰1.2，坝高为5米。

现为了提高堤坝的防洪抗洪能力，市防汛指挥部决定加固堤坝，要求坝顶CD 加宽1米，形成新的背水坡EF ，其坡度为1︰1.4。

已知堤坝总长度为4000米。

（1）求完成该工程需要多少土方？（4分）（2）该工程由甲、乙两个工程队同时合作完成，按原计划需要20天。

准备开工前接到上级通知，汛期可能提前，要求两个工程队提高工作效率。

甲队工作效率提高30%，乙队工作效率提高40%，结果提前5天完成。

问这两个工程队原计划每天各完成多少土方？（5分）（安徽）16.小明站在A 处放风筝，风筝飞到C 处时的线长为20米，这时测得∠CBD=60°，若牵引底端B 离地面1.5米，求此时风筝离地面高度。

2008年某某省各地中考数学试题精选几 何 解 答 题（1） 2008年某某省某某市中考数学几何解答题（08某某某某22题）22．如图9，教室窗户的高度AF 为米，遮阳蓬外端一点D 到窗户上椽的距离为AD ，某一时刻太阳光从教室窗户射入室内，与地面的夹角BPC ∠为30，PE 为窗户的一部分在教室地面所形成的影子且长为3米，试求AD 的长度．（结果带根号） （08某某某某22题解答）解：过点E 作EG AC ∥交于PD 于G 点 ··············································································· 1分 3tan 30313EG EP ==⨯= ··········· 3分 1BF EG ∴== ······································ 4分 即 2.51 1.5AB AF BF =-=-= ······························································· 5分 在Rt ABD △中， 1.533tan 30233AB AD ===（米） ··································· 7分AD ∴的长为332米 ·············································································· 8分（08某某某某25题）25．如图12，已知：边长为1的圆内接正方形ABCD 中，P 为边CD 的中点，直线AP 交圆于E 点．（1）求弦DE 的长．（2）若Q 是线段BC 上一动点，当BQ 长为何值时，三角形ADP 与以Q C P ，，为顶点的三角形相似．（08某某某某25题解答）（1）如图1．过D 点作DF AE ⊥于F 点．在Rt ADP △中，2252AP AD DP =+=················································· 1分 又1122ADP S AD DP AP DF ==△ 图9BADEPC图12A DB F CEP G22题图DF∴=··························································································· 2分AD的度数为9045DEA∴∠=DE∴==············································································· 4分（2）如图2．当Rt RtADP QCP△∽△时有AD DPQC CP=得：1QC=．即点Q与点B重合，0BQ∴= ··································································· 5分如图3，当Rt RtADP PCQ△∽△时，有AD PDPC QC=得14QC=，即34BQ BC CQ=-=····························································· 7分∴当0BQ=或34BQ=时，三角形ADP与以点Q C P，，为顶点的三角形相似．· 8分（2）2008年某某省某某市中考数学几何解答题（08某某某某） 19.（本题6分）如图，点D，E在BC上，且FD∥AB，FE∥AC.求证：△ABC∽△FDE.（08某某某某） 19.证明∵FD∥AB，∴∠B=∠FDE ∵FE∥AC ∴∠C=∠FED∴△ABC∽△FDEE25题图1E25题图2 25题图3FED CBA（08某某某某）22.（本题8分）如图，AB 是⊙O 的直径，AC 是弦，∠BAC 的平分线AD 交⊙O 于点D ，DE ⊥AC ，交AC 的延长线于点交AD 于点F.（1）求证：DE 是⊙O 的切线；（2）若35AC AB =，求AFDF的值.（08某某某某）22.⑴略证 连结OD ，可得∠ODA=∠OAD=∠DAC ∴OD ∥AE 又AE ⊥DE∴DE ⊥OD ，又OD 为半径 ∴DE 是的⊙O 切线 ⑵提示：过D 作DH ⊥AB 于H 则有∠DOH=∠CAB Cos ∠DOH=cos ∠CAB=35AC AB = 设OD=5x ，则AB=10x ，OH=3x ，DH=4x ∴AH=8x AD 2=80x 2由△AED ∽△ADB 可得 AD 2=AC ·AB=AC ·10x ∴AE=8X 又由△AEF ∽△DOF 可得AF ∶DF=AE ∶OD =85；∴AF DF =85（08某某某某）24.（本题10分）正方形ABCD 中，点O 是对角线AC 的中点，P 为对角线AC 上一动点，过点P 作PF ⊥DC 于点F.如图1，当点P 与点O 重合时，显然有DF ＝CF.（1）如图2，若点P 在线段AO 上（不与点A ，O 重合），PE ⊥PB 且PE 交CD 点E. ①求证：DF ＝EF ，②写出线段PC 、PA 、CE 之间的一个等量关系式，并证明你的结论：（2）若点P 在线段OC 上（不与点O ，C 重合），PE ⊥PB 且PE 交直线CD 于点E.请完成图3并判断（1）中的结论①、②是否分别成立？若不成立，写出相应的结论（所写结论均不必证明）.24.⑴①略；②PC －PA ＝2CE ；⑵结论①仍成立；结论②不成立，此时②中三条线段的数量关系是PA－PC ＝2CE ；F ED CBAOF P(O)DCBA图1图2OD CBAE F P O DCBA 图3P（3） 2008年某某省黄冈市中考数学几何解答题（08某某黄冈）14．（本题满分7分）已知：如图，点E 是正方形ABCD 的边AB 上任意一点，过点D 作DF DE ⊥交BC 的延长线于点F ．求证：DE DF =．（08某某黄冈）14．证明：∵四边形ABCD 为正方形， ∴AD=CD ，∠A=∠DCF=∠ADC=90°………………2分 又∵DF ⊥DE ∴∠EDF=90°………………………3分 ∴∠ADC=∠EDF 即∠1+∠3=∠2+∠3∴∠1=∠2………………………………………………5分 ∴△ADE ≌△CDF ∴DE=DF …………7分（08某某黄冈）16．（本题满分8分）已知：如图，在ABC △中，AB AC =，以AB 为直径的O 交BC于点D ，过点D 作DE AC ⊥于点E ． 求证：DE 是O 的切线．证明：连结OD ，则OD=OB ∴∠B=∠1…………1分 ∵AB=AC ∴∠B=∠C ……………………………2分 ∴∠1=∠C ………………………………………… 3分 ∴OD ∥AC ………………………………………… 4分 ∴∠ODE=∠DEC …………………………………… 5分 ∵DE ⊥AC ∴∠DEC=90°……………………… 6分 ∴∠ODE=90°即DE ⊥OD ………………………… 7分 ∴DE 是⊙O 的切线………………………………… 8分（08某某黄冈）17．（本题满分8分）如图是“明清影视城”的圆弧形门，黄红同学到影视城游玩，很想知道这扇门的相关数据．于是她从景点管理人员处打听到：这个圆弧形门所在的圆与水平地面是相切的，20AB CD ==cm ，200BD =cm ，且AB CD ，与水平地面都是垂直的．根据以上数据，请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少？A EBCFD 123DECA OBA C（08某某黄冈）17连接AC ，作AC 的中垂线交AC 于G ，交BD 于N ，交圆的另一点为M ，由垂径定理可知：MN 为圆的直径，N 点为圆弧形所在的圆与地面的切点。

2008 年中考数学几何选择题汇编（三角形部分） 1（08黑龙江鸡西）20．如图，将ABC △沿DE 折叠，使点A 与BC 边的中点F 重合，下列结论中：①EF AB ∥且12EF AB =；②BAF CAF ∠=∠；③12ADFE S AF DE = 四边形；④2BDF FEC BAC ∠+∠=∠，正确的个数是（ B ）A ．1B ．2C ．3D ．42（08黑龙江大庆）9．如图，将非等腰ABC △的纸片沿DE 折叠后，使点A 落在BC 边上的点F 处．若点D 为AB 边的中点，则下列结论：①BDF △是等腰三角形；②DFE CFE ∠=∠；③DE 是ABC △的中位线，成立的有（ ）A ．①②B ．①③C ．②③D ．①②③3（08黑龙江大庆）10．如图，在ABC △中，AC BC AB =>，点P 为ABC △所在平面内一点，且点P 与ABC △的任意两个顶点构成PAB PBC PAC △，△，△均是．．等腰三角形，则满足上述条件的所有点P 的个数为（ ） A ．3 B ．4C ．6D ．74（08辽宁沈阳）6．若等腰三角形中有一个角等于50，则这个等腰三角形的顶角的度数为（ D ） A ．50B ．80C ．65 或50D ．50 或806（08山西太原）3．在ABC △中，4080B C ∠=∠=，，则A ∠的度数为（ D ） A ．30B ．40C ．50D ．607（08山西太原）4．如图，在ABC △中，D E ，分别是边AB AC ，的中点， 已知10BC =，则DE 的长为（ C ）A ．3B ．4C ．5D ．68（08山西太原）8．如果三角形的两边分别为3和5，那么这个三角形的周长可能是（ A ） A ．15 B ．16 C ．8 D ．79（08山东济宁）9．如图，ABC △是等腰直角三角形，BC 是斜边，将ABP △绕点A 逆时针旋转后，能与ACP '△重合，如果3AP =，那么PP '的长等于（ A ） A． B．C．D．F第20题F（第9题） C （第10题）B A A D EB C10（08山东泰安）8．直角三角形纸片的两直角边长分别为6，8，现将ABC △如图那样折叠，使点A 与点B 重合，折痕为DE ，则tan CBE ∠的值是（ C ）A ．247 B．3C ．724D ．1311（08山东潍坊）6．如图，Rt ABC △中，AB AC ⊥，3AB =，4AC =，P是BC 上一点，作PE AB ⊥于E ，PD AC ⊥于D ，设BP x =， 则PD PE +=（ ）A ．35x +B ．45x-C ．72D ．21212525x x -12（08山东潍坊）8．如图，Rt ABC △中，AB AC ⊥，AD BC ⊥，BE 平分ABC ∠，交AD 于E ，EF AC ∥，下列结论一定成立的是（ ）A ．AB BF = B ．AE ED =C ．AD DC =D ．ABE DFE =∠∠13（08山东烟台）12、如图，在Rt △ABC 内有边长分别为,,a b c 的三个正方形，则,,a b c 满足的关系式是（ ）AA 、b a c =+B 、b ac =C 、222b ac =+ D 、22b a c ==14（08山东枣庄）3．如图，已知△ABC 为直角三角形，∠C =90°，若沿图中虚线剪去∠C ，则∠1＋∠2等于BA ．315° B．270° C ．180° D．135°15（08年江苏常州）15.如图,在△ABC 中,若DE ∥BC,AD DB =12,DE=4cm,则BC 的长为【 】 A.8cmB.12cmC.11cmD.10cm68 CEABD（第8题）ADPBEE A BD FC第3题图C16（08年江苏南通）17．已知△ABC 和△A′B′C′是位似图形．△A′B′C′的面积为6cm 2，周长是△ABC 的一半．AB ＝8cm ，则AB 边上高等于 【B 】 A ．3 cm B ．6 cm C ．9cm D ．12cm 17（08年江苏无锡）16．如图，OAB △绕点O 逆时针旋转80到OCD △的位置， 已知45AOB ∠=，则AOD ∠等于（ D ） Ａ．55Ｂ．45Ｃ．40Ｄ．3518（08浙江嘉兴）3．如图，ABC △中，已知8AB =，6BC =，4CA =，DE 是中位线， 则DE =（ B ）A ．4B ．3C ．2D ．1 19（08浙江嘉兴）8．已知等腰三角形的一个内角为50，则这个等腰三角形的顶角为（ C ） A ．50B ．80C ．50 或80D ．40 或6520（08浙江省丽水）8．如图，在三角形ABC 中，AB ＞AC ，D 、E 分别是AB 、AC 上的点，△ADE 沿线段DE 翻折，使点A 落在边BC 上，记为A '．若四边形ADA E '是菱形，D则下列说法正确的是A . DE 是△ABC 的中位线B . AA '是BC 边上的中线 C . AA '是BC 边上的高D . AA '是△ABC 的角平分线21（08浙江温州）7．如图，在Rt ABC △中，CD 是斜边AB 上的中线，已知2CD =，3AC =， 则sin B 的值是（ C ）A ．23B ．32C ．34D ．4322（08浙江温州）10．以OA 为斜边作等腰直角三角形OAB ，再以OB 为斜边在OAB △外侧作等腰直角三角形OBC ，如此继续，得到8个等腰直角三角形（如图），则图中OAB △与OHI △的面积比值是（ C ） A ．32 B ．64 C ．128 D ．256（第16题）（第3题） A '（第8题）C ABD （第7题图）A（第10题图）（第8题）A ．B ．C ．D ．23 (08安徽省卷)10.在△ABC 中，AB=AC=5，BC=6，点M 为BC 中点，MN ⊥AC 于点N ，则MN 等于【 C 】 A.65 B. 95 C. 125 D. 16524（08江西省卷）8．下列四个三角形中，与右图中的三角形相似的是（ B ）25(08福建龙岩)16．如图，在边长为4的等边三角形ABC 中，AD 是BC 边上的高，点E 、F 是AD 上的两点，则图中阴影部分的面积是 （ C ）A ．43B ．33C ．23D ．326 (08福建南平)7．已知ABC DEF △∽△，相似比为3，且ABC △的周长为18，则DEF △的周长为（C ）A ．2B ．3C ．6D ．5427（08湖北鄂州）6．如图2，已知ABC △中，45ABC ∠=，4AC =，H 是高AD 和BE 的交点，则线段BH 的长度为（ B ）AB ．4C．D ．528（08湖北黄石）8．如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与左图中ABC △相似的是（ B ）29（08湖北黄石）12．如图，在等腰三角形ABC 中，120ABC ∠=，点P 是底边AC 上一个动点，M N ，分别是AB BC ，的中点，若PM PN +的最小值为2，则ABC △的周长是（D ）A ．2B ．2C ．4D ．4+A ．B ．C ．D ．ABCD C B AEH图2 ABCPMN30（08湖北荆州）3．将一直角三角板与两边平行的纸条如图所示放置，下列结论：（1）∠1＝∠2；（2）∠3＝∠4；（3）∠2+∠4＝90°；（4）∠4+∠5＝180°，其中正确的个数 是（ D ）A.1B.2C.3D.431（08湖北十堰）2．下列长度的三条线段，能组成三角形的是CA ．1cm ，2 cm ，3cmB ．2cm ，3 cm ，6 cmC ．4cm ，6 cm ，8cmD ．5cm ，6 cm ，12cm32（08湖北十堰）8．如图，点E 在AD 的延长线上,下列条件中能判断BC ∥AD 的是C A ．∠3=∠4 B ．∠A+∠ADC=180° C ．∠1=∠2 D ．∠A ＝∠533 (08湖北咸宁)8．如图，在Rt △ABC 中，AB AC =，D 、E 是斜边BC 上两点，且∠DAE =45°，将△ADC 绕点A 顺时针旋转90︒后，得到△AFB ，连接EF ，下列结论： ①△AED ≌△AEF ； ②△ABE ∽△ACD ； ③BE DC DE +=； ④222BE DC DE += 其中正确的是 【 B 】 A ．②④； B ．①④；C ．②③；D ．①③．34（08湖北襄樊）3．如图1，已知AD 与BC 相交于点O ，AB CD ∥，如果40B ∠= ，30D ∠=，则AOC ∠的大小为（ B ）A ．60B ．70C ．80D ．12035（08湖南常德）14．如图3，已知等边三角形ABC 的边长为2，DE 是它的中位线，则下面四个结论：（1）DE=1，（2）AB 边上的高为3，（3）△CDE ∽△CAB ，（4）△CDE 的面积与△CAB 面积之比为1：4.其中正确的有 （ D ） A ．1个 B ．2个 C ．3个 D ．4个(第3题图) C B 第4题图DA (第8题图）A B C D E FB图336（08湖南湘潭）3.如图，已知D 、E 分别是ABC ∆的AB 、 AC 边上的点，,DE BC //且1ADE DBCE S S :=:8, 四边形 那么:AE AC 等于（ B ） A ．1 : 9 B ．1 : 3 C ．1 : 8 D ．1 : 237（08湖南湘潭）5.已知ABC ∆中，AC =4，BC =3，AB =5，则sin A =（ A ）A. 35B. 45C. 53D. 3438（08湖南株洲）4．如图，在ABC ∆中，D 、E 分别是AB 、AC 边的中点，若 6BC =，则DE 等于 CA ．5B ．4C ．3D ．239（08湖南邵阳）8．如图（四），点P 是AB 上任意一点，ABC ABD ∠=∠，还应补充一个条件，才能推出A P C A P D △≌△．从下列条件中补充一个条件，不一定能．．．．推出A P C A P D△≌△的是（ B ） A ．BC BD =B ．AC AD = C ．ACB ADB ∠=∠ D ．CAB DAB ∠=∠40（08广东茂名）10．如图，△ABC 是等边三角形，被一平行于BC 的矩形所截，AB 被截成三等分，则图中阴影部分的面积是△ABC 的面积的 （ C ）Ａ．91 Ｂ．92Ｃ．31 Ｄ．9441（08广东汕头）6．已知ABC △的三边长分别为5，13，12，则ABC △的面积为（ A ） A ．30 B ．60 C ．78 D ．不能确定42（08贵州贵阳）6．如果两个相似三角形的相似比是1:2，那么它们的面积比是（ ）A ．1:2B ．1:4C ．D ．2:141（08贵州遵义）4、如图，OA=OB ，OC=OD ，∠O=500，∠D=350，则∠AEC 等于 ( A )A ．600B ．500C ．450D ．300B ACD E第4题B C D E A CA DPB 图（四） （（第10题图）B 第18题图 42（08四川成都）7如图，在△ABC 与△DEF 中，已有条件AB=DE ，还需添加两个条件才能使△ABC ≌△DEF ，不能添加的一组条件是（A ）∠B=∠E,BC=EF （B ）BC=EF ，AC=DF (C ）∠A=∠D ，∠B=∠E （D ）∠A=∠D ，BC=EF43(08四川乐山)7、如图（3）AD ⊥CD ，AB ＝13，BC ＝12，CD ＝3，AD ＝4，则sinB=AA 、513B 、1213 Ｃ、35 Ｄ、4544 (08四川内江)5．如图，在Rt ABC △中，90C∠，三边分别为a b c ，，， 则cos A 等于（ ） A ．acB ．a bC ．b aD ．b c45（08四川资阳）10．如图3，已知Rt△ABC≌Rt△DEC，∠E＝30°，D 为AB 的中点，AC ＝1，若△DEC 绕点D 顺时针旋转，使ED 、CD 分别与Rt△ABC 的直角边BC 相交于M 、N ，则当△DMN 为等边三角形时，AM 的值为BABCD ．146（08重庆市卷）8、若△ABC∽△DEF，△ABC 与△DEF 的相似比为2︰3，则S △ABC ︰S △DEF 为（）A 、2∶3B 、4∶9 C、2∶3 D 、3∶247（08陕西省卷）3、一个三角形三个内角的度数之比为2∶3∶7，这个三角形一定是（ D ） A ．直角三角形 B ．等腰三角形 C ．锐角三角形 D ．钝角三角形48（08青海省卷）18．如图，DEF △是由ABC △经过位似变换得到的，点O 是位似中心，D E F ，，分别是OA OB OC ，，的中点，则DEF △与ABC △的面积比是（ C ）A ．1:6B ．1:5C ．1:4D ．1:2BDCAACBa cb（5题图）图349（08新疆区卷）7．如图，ABC △中BC 边上的高为1h ，DEF △中DE 边上的高为2h ，下列结论正确的是（ C ）A ．12h h >B ．12h h <C ．12h h =D ．无法确定50（08新疆乌鲁木齐）5．某等腰三角形的两条边长分别为3cm 和6cm ，则它的周长为（ C ） A ．9cm B ．12cm C ．15cm D ．12cm 或15cm。

2008年中考试卷分类---函数与几何图形1. 如图，在直角梯形ABCD 中，DC ∥AB ，∠A=90°，AB=28cm ，DC=24cm ，AD=4cm ，点M 从点D 出发，以1cm/s 的速度向点C 运动，点N 从点B 同时出发，以2cm/s 的速度向点A 运动，当其中一个动点到达端点停止运动时，另一个动点也随之停止运动.则四边形AMND 的面积y （cm 2）与两动点运动的时间t （s ）的函数图象大致是（ D ） 2. 如图，已知正三角形ABC 的边长为1，E 、F 、G 分别是AB 、BC 、CA 上的点，且AE ＝BF ＝CG ，设△EFG 的面积为y ，AE 的长为x ，则y 关于x 的函数的图象大致是（ C ）3. （潍坊）如图，圆B 切y 轴于原点O ，过定点(A -作圆B 切线交圆于点P ．已知tan 3PAB =∠，抛物线C 经过A ，P 两点．（1）求圆B 的半径；（2）若抛物线C 经过点B ，求其解析式；（3）投抛物线C 交y 轴于点M ，若三角形APM 为直角三角形，求点M 的坐标．4. （威海）如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积； （2）求四边形MEFN 面积的最大值． （3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由． 解：（1）分别过D ，C 两点作DG ⊥AB 于点G ，CH ⊥AB 于点H ． ∵ AB ∥CD ， ∴ DG ＝CH ，DG ∥CH ． ∴ 四边形DGHC 为矩形，GH ＝CD ＝1．∵ DG ＝CH ，AD ＝BC ，∠AGD ＝∠BHC ＝90°，∴ △AGD ≌△BHC （HL ）．∴ AG ＝BH ＝2172-=-GH AB ＝3． ………2分 ∵ 在Rt △AGD 中，AG ＝3，AD ＝5，∴ DG ＝4．∴ ()174162ABCD S +⨯==梯形．（2）∵ MN ∥AB ，ME ⊥AB ，NF ⊥AB ，∴ ME ＝NF ，ME ∥NF ． ∴ 四边形MEFN 为矩形． ∵ AB ∥CD ，AD ＝BC ， ∴ ∠A ＝∠B ． ∵ ME ＝NF ，∠MEA ＝∠NFB ＝90°， ∴ △MEA ≌△NFB （AAS ）．∴ AE ＝BF ． 设AE ＝x ，则EF ＝7－2x ． ∵ ∠A ＝∠A ，∠MEA ＝∠DGA ＝90°， ∴ △MEA ∽△DGA ．∴DG ME AG AE =．∴ ME ＝x 34． ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN 矩形．当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．（3）能． 由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ． 即 =34x 7－2x ．解，得 1021=x ．∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFNS 正方形．5. （青岛）已知：如图①，在Rt ΔABC 中，∠C=900，AC=4cm ，BC=3cm ，点P 由B 出发沿BA 方向向点A 匀速运动，速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为t （s ）（0<t <2），解答下列问题：（1）当t 为何值时，PQ ∥BC ？（2）设ΔAQP 的面积为y （cm 2），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使线段PQ 恰好把Rt ΔABC 的周长和面积同时平分？若存在，求出此时t 的值；若不存在，说明理由；（4）如图②，连接PC ，并把ΔPQC 沿QC 翻折，得到四边形PQP ′C ，那么是否存在某一时刻t ，使四边形PQP ′C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由． 解：（1）在Rt △ABC 中，522=+=AC BC AB ，由题意知：AP = 5－t ，AQ = 2t ，若PQ ∥BC ，则△APQ ∽△ABC ，∴=AC AQ AB AP ，∴52t t -=，∴10=t ． （2）过点P 作PH ⊥AC 于H ． ∵△APH ∽△ABC ，A BE F G H B∴=BC PH AB AP ，∴=3PH 55t -，∴t PH 533-=，∴t t t t PH AQ y 353)533(221212+-=-⨯⨯=⨯⨯=．（3）若PQ 把△ABC 周长平分，则AP+AQ=BP+BC+CQ ．∴)24(32)5(t t t t -++=+-， 解得：1=t ．若PQ 把△ABC 面积平分，则ABC APQ S S ∆∆=21， 即－253t ＋3t =3．∵ t =1代入上面方程不成立，∴不存在这一时刻t ，使线段PQ 把Rt △ACB 的周长和面积同时平分． （4）过点P 作PM ⊥AC 于Ｍ，PN ⊥BC 于N ，若四边形PQP ′ C 是菱形，那么PQ ＝PC ． ∵PM ⊥AC 于M ，∴QM=CM ． ∵PN ⊥BC 于N ，易知△PBN ∽△ABC ． ∴AB BP AC PN =， ∴54tPN =， ∴54t PN =， ∴54tCM QM ==，∴425454=++t t t ，解得：910=t ． ∴当910=t 时，四边形PQP ′ C 是菱形．此时37533=-=t PM ， 9854==t CM ， 在Rt △PMC 中，9505816494922=+=+=CM PM PC ， ∴菱形PQP ′ C 边长为9505．6. （温州）如图，在Rt △ABC 中，∠A ＝90º，AB ＝6，AC ＝8，D ，E分别是边AB ，AC 的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ ⊥BC 于Q ，过点Q 作QR ∥BA 交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ ＝x ，QR ＝y ．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使△PQR 为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△，BNDH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=． （2）QR AB ∥，90QRC A ∴∠=∠=．C C ∠=∠，RQC ABC ∴△∽△， RQ QC AB BC ∴=，10610y x -∴=，即y 关于x 的函数关系式为：365y x =-+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=， 1C ∴∠=∠． 84cos 1cos 105C ∴∠===，45QM QP ∴=，1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=，6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BAC CR CA ==， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △为等腰三角形．7. （义乌）如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积；②当2<t <4时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使ΔPDE 为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由。

太贵 19.79％FOEDCB A2008年辽宁省大连市初中毕业中考数学升学统一考试试题本试卷1～8页，共150分，考试时间120分钟。

一、选择题(本题8小题，每小题3分，共24分)说明:将下列各题唯一正确的答案代号A 、B 、C 、D 填到题后的括号内。

1．在平面直角坐标系中，点P (2，3)在 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2．下列运算中，结果正确的是 ( ) A ．3412a a a ⋅= B ．1025a a a ÷= C ．235a a a += D ．43a a a -=3．2007年8月对列车服务情况进行了调查，其中不满意情况的百分比如图1，由图中的数据可知，列车服务最需要 改进的方面是 ( )A ．列车员态度B ．超载C ． 车厢卫生D ．物价太贵4．如图，两温度计读数分别为我国某地今年2月份某天的最 低气温与最高气温，那么这天的最高气温比最低气温高( ) A ．5°C B ．7°C C ．12°C D ．－12°C5．在共有15人参加的的“我爱祖国”演讲比赛中，参赛选手要想知道自己是否能进入前8名，只需要了解自己的成绩以及全部成绩的 ( )A ．中位数B ．众数C ．平均数D ．方差6．下列图形中，恰好能与图3拼成一个矩形的是 ( )DC B A 图 37．若运算程序为：输出的数比该数的平方小1．则输入 ( ) A ．10 B ．11 C ．12 D ．138．如图，梯形ABCD 中，AD ∥BC ，中位线EF 交BD 于点O ， 若FO －EO = 5，则BC －AD 为( )F EDC BAOCB二、填空题(本题共8小题，每小题3分，共24分) 说明：将答案直接填在题后的横线上。

9．若两圆的半径分别为5和2，圆心距为7，则这两个圆的位置关系是__________． 10．小明和小红练习射击，第一轮10枪打完后两人的成绩如图5，一般新手的成绩不太稳定，小明和小红二人有一人是新手，估计小明和小红两人中新手是______________．11．关于x 的某个不等式组的解集在数轴上表示为如图6，则不等式组的解集为_________________________．12．如图，锐角三角形ABC 的边AB 和AC 上的高线CE 和BF 相交于点D ． 请写出图中的一对相似三角形______________________．13．△ABC 平移到△DEF ，若AD = 5，则CF 为_____________． 14．反比例函数k y x=的图象经过点(2，3)，则这个反比例函数的解析式为_______________．15．如图，画出△OAB 绕O 点按逆时针方向旋转90°时 的△OA ′B ′． 16．若12x =，12y =，则x + y 的值为______________．三、解答题(本题共4小题，其中17、18题各9分， 19题10分，20题各12分，共40分)17．化简：222931693aa a a a a a--÷++++18．如图，一块长方形铁皮的长是宽的2倍，四个角各截去一个正方形，制成高是5cm ，容积是500cm 3的无盖长方体容器，求这块铁皮的长和宽．19．如图，PA 、PB 是⊙O 的切线，切点分别为A 、B 、C 是⊙O 上一点，若∠APB = 40°，求∠ACB 的度数．20．某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个，在不将袋中球倒出来的情况下，分小组进行摸球试验，两人一组，共20组进行摸球实验．其中一位学生摸球，另一位学生记录所摸球的颜色，并将球放回袋中摇匀，每一组做400次试验，汇兑起来后，摸到红球次数为6000次．⑴估计从袋中任意摸出一个球，恰好是红球的概率是多少？⑵请你估计袋中红球接近多少个？四、解答题(本题共3小题，其中21、22题各10分，23题各8分，=+的图象经过点(2，0)、(－1y ax bx⑴求二次函数的解析式；⑵不用列表，在下图中画出函数图象，观察图象写出y > 022．为了测得学校旗杆的高度，小明先站在地面的A点测得旗杆最高点C的仰角为27°(点A 距旗杆的距离大于50m)，然后他向旗杆的方向向前进了50m，此时测得点C的仰角为40度．又已知小明的眼睛离地面1.6m，请你画出小明测量的示意图，并帮小明计算学校旗杆的高度．(精确到0.1m)．23．某仓库甲、乙、丙三辆运货车，每辆车只负责进货或出货，每小时的运输量丙车最多，乙四最少，乙车的运输量为每小时6吨，下图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图象，OA段只有甲、丙车工作，AB段只有乙、丙车工作，BC段只有甲、乙工作．⑴从早晨上班开始，库存每增加2吨，需要几小时？⑵问甲、乙、丙三辆车，谁是进货车，谁是出货车？⑶若甲、乙、丙三车一起工作，一天工作8小时，仓库的库存量有什么变化？图24-1五、解答题和附加题(本题共3小题，24题 10分，25题14分，26题10附加题5分，全卷累积不超过150分，建议考生最后答附加题)24．如图24－1，抛物线2y x =的顶点为P ，A 、B 是抛物线上两点，AB ∥x 轴，四边形ABCD 为矩形，CD 边经过点P ，AB = 2AD ． ⑴求矩形ABCD 的面积；⑵如图24－2，若将抛物线“2y x =”，改为抛物线“2y x bx c =++”，其他条件不变，请猜想矩形ABCD 的面积；⑶若将抛物线“2y x bx c =++”改为抛物线“2y ax bx c =++请猜想矩形ABCD 的面积(用a 、b 、c 表示，并直接写出答案)．附加题：若将24题中“2y x =”改为“2y ax bx c =++”，“AB 条件不要，其他条件不变，探索矩形ABCD 面积为常数时，矩形要满足什么条件？并说明理由．25．如图25－1，正方形ABCD和正方形QMNP，∠M =∠B，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．⑴求证：ME = MF．⑵如图25－2，若将原题中的“正方形”改为“菱形”，其他条件不变，探索线段ME与线段MF的关系，并加以证明．⑶如图25－3，若将原题中的“正方形”改为“矩形”，且AB = m BC，其他条件不变，探索线段ME与线段MF的关系，并说明理由．⑷根据前面的探索和图25－4，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题；若不能，请说明理由．图25 - 4图25 - 3图25 - 2图25 -1G FE CBAD26．如图，△ABC 的高AD 为3，BC 为4，直线EF ∥BC ，交线段AB 于E ，交线段AC 于F ，交AD 于G ，以EF 为斜边作等腰直角三角形PEF (点P 与点A 在直线EF 的异侧)，设EF 为x ，△PEF 与四边形BCEF 重合部分的面积为y ．⑴求线段AG (用x 表示)；⑵求y 与x 的函数关系式，并求x 的取值范围．。

2008年全国中考数学压轴题精选精析（一）1．（08广东中山22题）将两块大小一样含30°角的直角三角板，叠放在一起，使得它们的斜边AB 重合，直角边不重合，已知AB=8，BC=AD=4，AC 与BD 相交于点E ，连结CD ．(1)填空：如图9，AC= ，BD= ；四边形ABCD 是 梯形. (2)请写出图9中所有的相似三角形（不含全等三角形）. (3)如图10，若以AB 所在直线为x 轴，过点A 垂直于AB 的直线为y 轴建立如图10的平面直角坐标系，保持ΔABD 不动，将ΔABC 向x 轴的正方向平移到ΔFGH 的位置，FH 与BD 相交于点P ，设AF=t ，ΔFBP 面积为S ，求S 与t 之间的函数关系式，并写出t 的取值值范围.（08广东中山22题解析）解：（1）1分等腰；…………………………2分（2）共有9对相似三角形.（写对3－5对得1分，写对6－8对得2分，写对9对得3分）①△DCE 、△ABE 与△ACD 或△BDC 两两相似，分别是：△DCE ∽△ABE ，△DCE ∽△ACD ，△DCE ∽△BDC ，△ABE ∽△ACD ，△ABE ∽△BDC ；(有5对)②△ABD ∽△EAD ，△ABD ∽△EBC ；(有2对) ③△BAC ∽△EAD ，△BAC ∽△EBC ；(有2对)所以，一共有9对相似三角形.…………………………………………5分（3）由题意知，FP ∥AE ， ∴ ∠1＝∠PFB ， 又∵ ∠1＝∠2＝30°， ∴ ∠PFB ＝∠2＝30°,∴ FP ＝BP (6)过点P 作PK ⊥FB 于点K ，则F K B K =∵ AF ＝t ，AB ＝8， ∴ FB ＝8－t ，1(8)2B K t =-.在Rt △BPK 中，1tan 2(8)tan 30)26PK BK t t =⋅∠=-︒=-. ……………………7分∴ △FBP 的面积11(8)(8)226S FB PK t t =⋅⋅=⋅-⋅-，∴ S 与t 之间的函数关系式为：DCBE图9图1028)12S t =-，或24123S t =-+…………………………………8分t 的取值范围为：08t ≤<. …………………………………………………………9分2.（08湖北十堰25题）已知抛物线b ax ax y ++-=22与x 轴的一个交点为A(-1,0)，与y 轴的正半轴交于点C ．⑴直接写出抛物线的对称轴，及抛物线与x 轴的另一个交点B 的坐标；⑵当点C 在以AB 为直径的⊙P 上时，求抛物线的解析式；⑶坐标平面内是否存在点M ，使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形？若存在，请求出点M 的坐标；若不存在，请说明理由．（08湖北十堰25题解析）解：⑴对称轴是直线：1=x ，点B 的坐标是(3,0)． ……2分说明：每写对1个给1分，“直线”两字没写不扣分．⑵如图，连接PC ，∵点A 、B 的坐标分别是A(-1,0)、B (3,0)， ∴AB ＝4．∴．AB PC 242121=⨯==在Rt △POC 中，∵OP ＝PA －OA ＝2－1＝1， ∴．POPCOC 3122222=-=-=∴b ＝．3 ………………………………3分 当01=-=，y x 时，，a a 032=+--∴．a 33= ………………………………4分∴．x x y 3332332++-= ………………5分⑶存在．……………………………6分理由：如图，连接AC 、BC ．设点M 的坐标为),(y x M ．①当以AC 或BC 为对角线时，点M 在x 轴上方，此时CM ∥AB ，且CM ＝AB ．由⑵知，AB ＝4，∴|x|＝4，3==OC y ．∴x ＝±4．∴点M 的坐标为)3,4()3,4(-或M ．…9分说明：少求一个点的坐标扣1分．②当以AB 为对角线时，点M 在x 轴下方． 过M 作MN ⊥AB 于N ，则∠MNB ＝∠AOC ＝90°． ∵四边形AMBC 是平行四边形，∴AC ＝MB ，且AC ∥MB ．∴∠CAO ＝∠MBN ．∴△AOC ≌△BNM ．∴BN ＝AO ＝1，MN ＝CO ． ∵OB ＝3，∴0N ＝3－1＝2．∴点M 的坐标为(2,M ． ……………………………12分说明：求点M 的坐标时，用解直角三角形的方法或用先求直线解析式，然后求交点M 的坐标的方法均可，请参照给分．综上所述，坐标平面内存在点M ，使得以点A 、B 、C 、M 为顶点的四边形是平行四边形．其坐标为123((2,M M M -．说明：①综上所述不写不扣分；②如果开头“存在”二字没写，但最后解答全部正确，不扣分。

2008年中考试题汇编全等三角形一、选择1、(2008 台湾)如图，有两个三角锥ABCD、EFGH，其中甲、乙、丙、丁分别表示ABC、ACD、 EFG、EGH。

若ACB=CAD=EFG=EGH=70，BAC=ACD=EGF=EHG =50，则下列叙述何者正确？ ( )(A)甲、乙全等，丙、丁全等 (B) 甲、乙全等，丙、丁不全等(C) 甲、乙不全等，丙、丁全等 (D) 甲、乙不全等，丙、丁不全等2．（2008年江苏省无锡市）如图，绕点逆时针旋转到的位置，已知，则等于（）Ａ．Ｂ．Ｃ．Ｄ．3、（2008山东潍坊）如图, Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC，交AD于E，EF∥AC，下列结论一定成立的是（）A.AB=BFB.AE=EDC.AD=DCD.∠ABE=∠DFE，二、填空1.（2008佳木斯市3）如图，，请你添加一个条件：，使（只添一个即可）．2.（2008年江苏省南通市）已知：如图，△OAD≌△OBC，且∠O＝70°，∠C ＝25°，则∠AEB＝________度.3、(2008年荷泽市)如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下五个结论：① AD=BE；② PQ∥AE；③ AP=BQ；④ DE=DP；⑤ ∠AOB=60°．恒成立的结论有______________（把你认为正确的序号都填上）．4.（2008海南省）已知在△ABC和△A1B1C1中，AB=A1B1，∠A=∠A1，要使△ABC≌△A1B1C1，还需添加一个条件，这个条件可以是 .5、(2008 湖北天门)如图，已知AE＝CF，∠A＝∠C，要使△ADF≌△CBE，还需添加一个条件____________________(只需写一个)．6. (08仙桃等)如图，中，点的坐标为（0，1），点的坐标为（4，3），如果要使与全等，那么点的坐标是 .三、解答题1、（2008山西太原）将一张透明的平行四边形胶片沿对角线剪开，得到图①中的两张三角形胶片和。

2008年大连市䌜毕业升学统一考试旅顺口区试测(一)数学本试卷1～8页，共150分，考试时间120分钟。

一、选择题(本题8小题，每小题3分，共24分)说明:将下列各题唯一正确的答案代号A、B、C、D填到题后的括号内。

1．如图，小明用手盖住的点的坐标可能为( )A．(2，3)B．(2，－3) C．(－2，3) D．(－2，－3)2．下图为各届夏季奥运会的会徽图案，其中是轴对称图形的是（）A．B．C．D．3．下列运算中，正确．．的是( )A．24=B．623-=-C．22)(abab=D．2523aaa=+4．如图所示是某校九年级学生到校方式的条形统计图，根据图形可得出步行人数占总人数的( )A．60％B．50％C．30％D．20％5．已知⊙O1的半径为5cm，⊙O2的半径为3cm，圆心距O1O2＝2，那么⊙O1与⊙O2的位置关系是（）A．相离B．外切C．相交D．内切6．测得某人的一根头发直径约为0.000 072 85米，用科学记数法表示为( )A．7285×10－8米B．7.285×10－5 米C．0.7285×14－4 米D．0.7285×10－5米7．均匀地向一个如图所示的容器中注水，最后把容器注满，在注水过程中水面高度h随时间t变化的函数图象大致是（）.2008年北京1992年巴塞罗那1980年莫斯科1972年慕尼黑yxO二、填空题(本题共8小题，每小题3分，共24分)说明：将答案直接填在题后的横线上。

9．如果某天中午气温是2°C ，到了傍晚气温下降了5°C ，那么傍晚的气温是__________C°．1011个地区当天最高气温（℃）统计如下表：那么这些城市当天的最高气温的中位数和众数分别是________，_________．11．不等式组21040x x ->⎧⎨-≥⎩的解集是________________．12．小明的身高是1.7m ，他的影长是2m ，同一时刻学校旗杆的影长是10m ，则旗杆的高是_________m ．13．如图，P 为正方形ABCD 内的一点，△ABP 绕点B 顺时针旋转得到△CBE ，则△BPE 是 三角形．14．矩形的面积为2，一条边长为x ，另一条边长为y ，则y 与x 的函数关系式为(不必写出自变量取值范围)____________________．15．如图，△ABC 后的图形是△A ′B ′C ′，其中C 与C ′是对应点，请画出平移后的三角形△A ′B ′C ′．16．已知二次函数22y x x m =-++的部分图象如图所示，则关于x 的一元二次方程220x x m -++=的解为 ．EPDCBA16题图15题图13题图三、解答题(本题共4小题，每题10分，共40分)17．已知22212211x x y x x x x x -=÷---++，当x 为何值时，y 的值为12．18．红星超市07年十月份的营业额为4万元，第四季度的总营业额是13.24万元，求十一、十二月份平均每月增长的百分率.19．如图，在4×3的正方形网格中，△ABC 与△DE C 的顶点都在边长为1的小正方形的顶点上。

2008 年中考数学几何解答题 三角形1.(08市卷15题)15．（本小题满分5分）已知：如图，C 为BE 上一点，点A D ，分别在BE 两侧．AB ED ∥，AB CE =，BC ED =． 求证：AC CD =． 证明： 证明：AB ED ∥，B E ∴∠=∠．……2分在ABC △和CED △中，AB CE B E BC ED =⎧⎪∠=∠⎨⎪=⎩，，， ABC CED ∴△≌△． ·············································································· 4分 AC CD ∴=． ························································································· 5分2.（08某某某某）24．（本小题满分6分） 如图，在ABC △中，2BAC C ∠=∠．（1）在图中作出ABC △的内角平分线AD ．（要求：尺规作图，保留作图痕迹，不写证明）（2）在已作出的图形中，写出一对相似三角形，并说明理由．24．解：（1）如图，AD 即为所求． ···················· 2分 （2）ABD CBA △∽△，理由如下． ················· 3分AD 平分2BAC BAC C ∠∠=∠，，BAD BCA ∴∠=∠． ······································· 5分 又B B ∠=∠，ABD CBA ∴△∽△． ··············· 6分3.（08年某某某某）(本小题满分7分)已知:如图,AB=AD,AC=AE,∠BAD=∠CAE.求证:AC=DE.（第22题）ABCDABCDACEDB（第21题图）DCBA4.（08年某某某某）（A 类）已知如图，四边形ABCD 中，AB ＝BC ，AD ＝CD ，求证：∠A ＝∠C. （B 类）已知如图，四边形ABCD 中，AB ＝BC ，∠A ＝∠C ，求证：AD ＝CD.证明：（A ）连结AC ，因为AB ＝AC ，所以∠BAC ＝∠BCA ，同理AD ＝CD 得∠DAC ＝∠DCA所以∠A ＝∠BAC ＋∠DAC ＝∠BCA ＋∠DCA ＝∠C （B ）如（A ）只须反过来即可.5. (08某某某某)20．（10分）如图，∠A =36°，∠DBC =36°，∠C =72°，找出图中的一个等腰三角形，并给予证明.我找的等腰三角形是：. 证明：我所找的等腰三角形是：△ABC （或△BDC 或△DAB ）…4分 证明：在△ABC 中，∵∠A =36°，∠C =72°，∴∠ABC =180°－（72°＋36°）=72°. ………………………………… 7分∵∠C =∠ABC ， ∴AB =AC ，∴△ABC 是等腰三角形. …………………………………………………………… 10分DC BA[注]若找△BDC 或△DAB 参照给分.6. (08某某某某)21、（8分）已知：如图，E 、C 两点在线段BF 上，BE=CF ，AB=DE ，AC=DF 。

某某 周建杰 分类（2008年某某市）7．如左下图，现有一扇形纸片，圆心角∠AOB 为120°，弦AB 的长为23cm ，用它围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为A ．32cmB ．π32cmC ．23cmD ．π23cm（2008年某某市）21．计算：01)41.12(45tan 32)31(-++--- ．（2008年某某市）23．（6分）如图，山顶建有一座铁塔，塔高30m CD =，某人在点A 处测得塔底C 的仰角为20，塔顶D 的仰角为23，求此人距CD 的水平距离AB ． （参考数据：sin 200.342≈，cos 200.940≈，tan 200.364≈，sin 230.391≈，cos 230.921≈，tan 230.424≈）以下是某某省高建国分类：（2008年某某市）又到了一年中的春游季节，某班学生利用周末到白塔山去参观“晏阳初博物馆”．下面是两位同学的一段对话： 甲：我站在此处看塔顶仰角为60 乙：我站在此处看塔顶仰角为30 甲：我们的身高都是 乙：我们相距20m请你根据两位同学的对话，计算白塔的高度（精确到1米）．（第23题）ABCD 2023（2008年某某市）已知α为锐角，且cot （90°－α）＝3，则α的度数为（ ） A ．30° B ．60° C ．45° D ．75°（2008年某某市）如图是一个中心对称图形，A 为对称中心，若∠C=90°，∠B=30°，BC=1，则BB ’的长为（ ）A ．4B ．33 C ．332 D ．334 （2008年某某市）我市准备在相距2千米的A 、B 两工厂间修一条笔直的公路，但在B 地北偏东60°方向、A 地北偏西45°方向的C 处，有一个半径为的住宅小区（见下图），问修筑公路时，这个小区是否有居民需要搬迁？（参考数据：41.12≈73.13≈）（2008年某某市）19．（本题满分10分）如图7，某拦河坝截面的原设计方案为：AH BC ∥，坡角74ABC ∠=，坝顶到坝脚的距离6m AB =．为了提高拦河坝的安全性，现将坡角改为55，由此，点A 需向右平移至30°ACB ’BC ’点D ，请你计算AD 的长（精确到）．（2008年某某市）24．（10分）我市某乡镇学校教学楼后面靠近一座山坡，坡面上是一块平地，如图所示．BC AD ∥，斜坡40AB =米，坡角60BAD ∠=，为防夏季因瀑雨引发山体滑坡，保障安全，学校决定对山坡进行改造．经地质人员勘测，当坡角不超过45时，可确某某体不滑坡，改造时保持坡脚A 不动，从坡顶B 沿BC 削进到E 处，问BE 至少是多少米（结果保留根号）？以下是某某康海芯的分类: 1.（2008年某某市）计算：201()2sin 3032--+︒+-2.（2008年某某市）汶川地震后，抢险队派一架直升飞机去A 、B 两个村庄抢险，飞机在距地面450米上空的P 点，测得A 村的俯角为30︒，B 村的俯角为60︒（．如图7）．求A 、B 两个村庄间的距离．1.414 1.732==）某某省 岳伟 分类（24题图）（24题图）（图7）ABDH55C FE （图7）ABCDH552008年某某市1、如图，在Ｒt △ＡＢＣ中，∠Ｃ＝900,∠Ａ＝300,Ｅ为ＡＢ上一点且ＡＥ：ＥＢ＝4：1 ， ＥＦ⊥ＡＣ于Ｆ，连结ＦＢ，则tan ∠CFB 的值等于（ ）32353A 53333、 Ｂ、 Ｃ、 Ｄ、 2008年某某市2、计算：0120082cos 453+--1（）（）3、汶川地震后，抢险队派一架直升飞机去A 、B 两个村庄抢险，飞机在距地面450米上空的P 点，测得A 村的俯角为30︒，B 村的俯角为60︒（．如图7）．求A 、B 两个村庄间的距离．（结果精确到米，参考数据2 1.4143 1.732==，） 答：10．(2008年某某市)如图，已知直角三角形ABC 中，斜边AB 的长为m ，40B ∠=，则直角边BC 的长是（ B ） A ．sin 40mB ．cos 40mC ．tan 40mD ．tan 40mQB CP A45060︒30︒图7ADBE图6i =1:3CF EDCBA1:3i =以下是某某省马某某市成功中学的汪宗兴老师的分类1．(2008年·某某市)（本题满分7分）如图6，梯形ABCD 是拦水坝的横断面图，（图中3:1=i 是指坡面的铅直高度DE 与水平宽度CE 的比），∠B=60°，AB=6，AD=4，求拦水坝的横断面ABCD 的面积．（结果保留三位有效数字.参考数据：3≈1.732，2≈1.414）答案：过点A 作AF ⊥BC ，垂足为点F.解析：这是利用三角形函数解直角三角形解决实际问题，拦水坝的横断面是梯形，求其面积可通过作高巧妙地将梯形面积问题转化为两个直角三角形和一个矩形的问题，有关四边形的许多问题都可以通过添加适当地辅助线将其转化三角形的问题，这正体现了数学中的转化思想。