几种重要的连续型分布

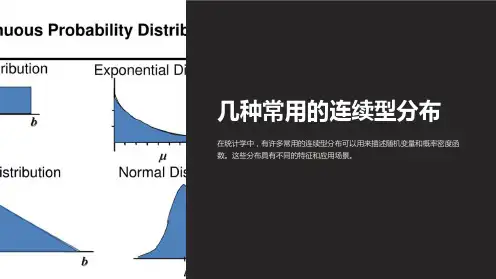
概率分布的种类与性质概率分布是概率论中的重要概念，用于描述随机变量的取值与其对应的概率。

不同的随机变量具有不同的概率分布，而概率分布又可以分为多种种类。

本文将介绍常见的概率分布种类及其性质。

一、离散型概率分布离散型概率分布是指随机变量取有限个或可数个值的概率分布。

常见的离散型概率分布有以下几种：1. 伯努利分布（Bernoulli Distribution）伯努利分布是最简单的离散型概率分布，它描述了只有两个可能结果的随机试验，如抛硬币的结果（正面或反面）。

伯努利分布的概率质量函数为：P(X=k) = p^k * (1-p)^(1-k)，其中k=0或1，p为成功的概率。

2. 二项分布（Binomial Distribution）二项分布是一种重要的离散型概率分布，它描述了n次独立重复的伯努利试验中成功次数的概率分布。

二项分布的概率质量函数为： P(X=k) = C(n,k) * p^k * (1-p)^(n-k)，其中k=0,1,...,n，C(n,k)为组合数，p为成功的概率。

3. 泊松分布（Poisson Distribution）泊松分布是一种用于描述单位时间或单位空间内随机事件发生次数的离散型概率分布。

泊松分布的概率质量函数为：P(X=k) = (λ^k * e^(-λ)) / k!，其中k=0,1,2,...，λ为平均发生率。

二、连续型概率分布连续型概率分布是指随机变量取值为连续区间内的概率分布。

常见的连续型概率分布有以下几种：1. 均匀分布（Uniform Distribution）均匀分布是一种简单的连续型概率分布，它在给定区间内的取值概率相等。

均匀分布的概率密度函数为：f(x) = 1 / (b-a)，其中a为区间下界，b为区间上界。

2. 正态分布（Normal Distribution）正态分布是一种重要的连续型概率分布，也被称为高斯分布。

正态分布具有钟形曲线，对称分布于均值周围。

下面介绍2个常用二维连续型随机变量分布1. 正态分布（Normal Distribution）：正态分布是最为常见的连续型随机变量分布之一，其概率密度函数（Probability Density Function，简称PDF）表达式如下：\[f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]其中，μ为分布的均值（即期望值），σ为分布的标准差。

正态分布的特点如下：-对称性：正态分布呈现中心对称的特点，均值μ处为分布的中心位置，左右两侧的概率密度相等；-单峰性：正态分布具有一个单峰，峰值即为μ处的概率密度最大值；-形态可变性：正态分布具有可调整的均值和标准差，通过调整这两个参数可以改变分布的形态；-中心极限定理：在许多随机现象中，大量独立同分布的随机变量经过适当的标准化后，其和的分布趋近于正态分布。

正态分布在实际应用中非常广泛，尤其在自然环境中具有重要地位，例如重量、身高、应力等现象通常会服从正态分布。

此外，正态分布在统计推断、假设检验等领域也有着重要的应用。

2. 指数分布（Exponential Distribution）：指数分布是一种表示事件间隔时间的连续型随机变量分布，其概率密度函数表达式如下：\[f(x) = \lambda e^{-\lambda x}\]其中，λ为分布的参数，表示单位时间内事件发生的平均次数。

指数分布的特点如下：-无记忆性：指数分布具有无记忆性的特点，即已经发生的时间不会影响未来事件的发生时间；-单峰性：指数分布呈现等概率下降的单峰分布，其概率密度随着时间的增加而递减；-非负性：指数分布的随机变量的取值范围为非负数。

指数分布在实际应用中有较广泛的应用，尤其与事件发生、生存分析等相关，例如到达时间、等待时间、设备寿命等都适合使用指数分布进行建模。

综上所述，正态分布和指数分布是两种常用的二维连续型随机变量分布。

二项式分布泊松分布高斯分布1.引言1.1 概述概述二项式分布、泊松分布和高斯分布是概率统计学中重要的概率分布函数，它们在各个领域的应用非常广泛。

本文将对这三种分布进行详细介绍和分析。

二项式分布是一种离散型概率分布，描述了在一系列独立重复的“成功-失败”试验中成功次数的概率分布情况。

它的定义和特点将在本文中详细探讨。

二项式分布的应用领域广泛，如生物学中对基因的遗传分析、市场调研中对顾客购买行为的研究等。

泊松分布是另一种离散型概率分布，用于描述在一段固定时间或空间内事件发生的次数的概率分布情况。

它的定义和特点也将在本文中进行详细解析。

泊松分布在很多实际问题中都有应用，比如电话交换机中呼叫数量的模型、自然灾害发生频率的统计等。

高斯分布，也被称为正态分布，是一种连续型概率分布，它是自然界和人类社会中很多现象的理想模型。

高斯分布的定义和特点将在后面的章节中进行详细介绍。

高斯分布广泛应用于各个领域，如物理学中的测量误差分析、金融学中的资产收益率分布建模等。

通过对这三种分布的探讨和比较，我们可以更好地理解它们的特点和应用。

同时，我们还可以进一步探讨它们之间的关系，如泊松分布在大样本条件下逼近二项式分布，以及中心极限定理中高斯分布的应用等。

最后，本文还会展望一下这些分布在未来的发展方向和可能的研究方向。

总之，本文将全面介绍二项式分布、泊松分布和高斯分布，包括它们的定义、特点和应用领域。

通过深入研究这些分布，我们可以更好地理解概率统计学中的核心概念，为实际问题的解决提供更准确的分析工具和方法。

1.2文章结构文章结构部分的内容可以按照以下方式编写：1.2 文章结构本文将按照以下结构进行探讨：2. 正文部分2.1 二项式分布2.1.1 定义和特点2.1.2 应用领域2.2 泊松分布2.2.1 定义和特点2.2.2 应用领域2.3 高斯分布2.3.1 定义和特点2.3.2 应用领域3. 结论部分3.1 总结3.2 对比与应用3.3 展望在正文部分，我们将逐一介绍二项式分布、泊松分布和高斯分布的定义、特点以及它们在实际应用中的领域。

连续型概率分布连续型概率分布是概率论中的一个重要概念，用于描述连续随机变量的可能取值范围及其对应的概率。

与离散型概率分布相比，连续型概率分布在数轴上的每一个点都有概率密度函数与之对应，而不是直接给出某个点的概率。

本文将介绍几种常见的连续型概率分布，包括均匀分布、正态分布和指数分布。

一、均匀分布均匀分布是一种简单而常见的连续型概率分布，它假设随机变量在一定的范围内取值的概率是相同的。

在数学上，均匀分布的概率密度函数为：f(x) = 1 / (b - a)，a ≤ x ≤ b其中，a和b分别表示均匀分布的下界和上界。

图表上，均匀分布的概率密度函数在[a, b]区间内的取值是一个常数，且在[a, b]之外为0。

这意味着在[a, b]区间内的任意一个子区间上，概率密度的积分就是该子区间的长度除以[a, b]之间的总长度。

二、正态分布正态分布是统计学中最重要的连续型概率分布之一，也被称为高斯分布。

正态分布在自然界和社会科学中的广泛应用使得它成为了研究的重点。

正态分布的概率密度函数可以写作：f(x) = 1 / (σ * √(2π)) * exp(-(x - μ)² / (2σ²))其中，μ是均值，σ是标准差。

正态分布的概率密度函数呈钟形曲线，其峰值位于μ处，标准差决定了曲线的形状。

正态分布具有许多重要的特性，如68-95-99.7法则，即大约68%的概率密度位于一个标准差范围内，95%位于两个标准差范围内，99.7%位于三个标准差范围内。

三、指数分布指数分布是描述连续随机事件发生的时间间隔的概率分布。

例如，某个服务台上的顾客到达时间间隔、两次地震发生的间隔等，都可以用指数分布来描述。

指数分布的概率密度函数可以写作：f(x) = λ * exp(-λx)，x ≥ 0其中，λ是分布的参数，表示单位时间内事件发生的平均次数。

指数分布的概率密度函数在区间[0, +∞)上递减，且总面积等于1。

指数分布还有一个重要的特性是无记忆性，即已经等待了一段时间后，再等待一段时间的概率与一开始等待这段时间的概率是相等的。

高考数学知识点精讲常见随机变量的分布类型高考数学知识点精讲：常见随机变量的分布类型在高考数学中，随机变量的分布类型是一个重要的知识点，理解和掌握这些分布类型对于解决概率相关的问题至关重要。

下面我们就来详细讲解一下常见的随机变量分布类型。

首先，我们来认识一下什么是随机变量。

简单来说，随机变量就是把随机试验的结果用数字表示出来。

比如说掷骰子，我们可以定义随机变量 X 为骰子掷出的点数，那么 X 可能取值 1、2、3、4、5、6。

常见的随机变量分布类型主要有以下几种：一、离散型随机变量的分布1、两点分布两点分布是最简单的一种离散型随机变量分布。

比如抛一枚硬币，正面朝上记为1，反面朝上记为0，那么这个随机变量就服从两点分布。

其概率分布为 P(X ＝ 1) ＝ p，P(X ＝ 0) ＝ 1 p ，其中 0 ＜ p ＜ 1 。

2、二项分布二项分布在实际生活中有很多应用。

比如进行n 次独立重复的试验，每次试验只有两种结果（成功或失败），成功的概率为 p ，失败的概率为 1 p 。

那么成功的次数 X 就服从二项分布，记为 X ～ B(n, p) 。

二项分布的概率公式为：P(X ＝ k) ＝ C(n, k) p^k （1 p)＾（n k) ，其中 C(n, k) 表示从 n 个元素中选出 k 个元素的组合数。

举个例子，假设一批产品的次品率为 02，从这批产品中随机抽取10 个，那么抽到次品个数 X 就服从二项分布 B(10, 02) 。

3、超几何分布超几何分布与二项分布有点类似，但适用的场景略有不同。

超几何分布是从有限 N 个物件（其中包含 M 个指定种类的物件）中抽出 n 个物件，成功抽出指定种类物件的次数 X 就是超几何分布。

超几何分布的概率公式为：P(X ＝ k) ＝ C(M, k) C(N M, n k) ／C(N, n) 。

比如说在一个有 50 个球，其中 20 个红球，30 个白球的盒子中，随机抽取 10 个球，红球的个数 X 就服从超几何分布。

概率分布计算公式概率分布是概率论中重要的概念之一，它描述了随机变量在各个取值上的取值概率。

在实际问题中，我们常常需要计算概率分布以解决相关的概率统计问题。

本文将介绍几种常见的概率分布以及它们的计算公式。

一、二项分布(Binomial Distribution)二项分布是概率论中常用的离散型概率分布，它描述了在一定次数的独立重复试验中，成功事件发生的次数的概率分布。

其计算公式为：P(X=k) = C(n, k) * p^k * (1-p)^(n-k)其中，P(X=k)表示成功事件发生k次的概率，n表示试验次数，p表示每次试验成功的概率，C(n, k)表示组合数，可以使用n个数任取k个的方式计算。

二项分布的期望为E(X)=np，方差为Var(X)=np(1-p)。

二、泊松分布(Poisson Distribution)泊松分布是一种离散型概率分布，适用于描述单位时间(或单位空间)内随机事件发生的次数。

其计算公式为：P(X=k) = (λ^k * e^(-λ))/k!其中，P(X=k)表示事件发生k次的概率，λ表示单位时间(或单位空间)内事件发生的平均次数，e为自然对数的底。

泊松分布的期望为E(X)=λ，方差为Var(X)=λ。

三、正态分布(Normal Distribution)正态分布是概率论中最重要的连续型概率分布，也称为高斯分布。

它的形状呈钟型曲线，对称于均值。

正态分布在实际问题中得到广泛应用。

其概率密度函数的计算公式为：f(x) = (1 / (σ * √(2π))) * e^((-1/2)*((x-μ)/σ)^2)其中，f(x)表示随机变量X的概率密度函数，μ为均值，σ为标准差，π为数学常数3.14159。

正态分布的期望为E(X)=μ，方差为Var(X)=σ^2。

四、指数分布(Exponential Distribution)指数分布是一种连续型概率分布，其概率密度函数具有常数倍衰减的特点。

,.第七讲连续型随机变量（续）及 随机变量的函数的分布3. 三种重要的连续型随机变量 （1）均匀分布设连续型随机变量X 具有概率密度)5.4(,,0,,1)(⎪⎩⎪⎨⎧<<-=其它b x a ab x f则称X 在区间(a,b)上服从均匀分布, 记为X~U(a,b).X 的分布函数为)6.4(.,1,,,,0)(⎪⎪⎩⎪⎪⎨⎧≥<≤--<=b x b x a a b a x a x x F（2）指数分布设连续型随机变量X 的概率密度为)7.4(,,0,0,e1)(/⎪⎩⎪⎨⎧>=-其它x x f x θθ其中θ>0为常数, 则称X 服从参数为θ的指数分布.容易得到X 的分布函数为第二章 随机变量及其分布§4 连续型随机变量 及其概率密度1=2,.)8.4(.,0,0,1)(/⎩⎨⎧>-=-其它x e x F x θ如X 服从指数分布, 则任给s,t>0, 有 P{X>s+t | X > s}=P{X > t} (4.9)事实上}.{e ee )(1)(1}{}{}{)}(){(}|{//)(t X P s F t s F s X P t s X P s X P s X t s X P s X t s X P t s t s >===-+-=>+>=>>⋂+>=>+>--+-θθθ性质(4.9)称为无记忆性.指数分布在可靠性理论和排队论中有广泛的运用.（3）正态分布设连续型随机变量X 的概率密度为)10.4(,,e21)(222)(∞<<-∞=--x x f x σμσπ其中μ,σ(σ>0)为常数, 则称X 服从参数为μ,σ的正态分布或高斯(Gauss)分布, 记为X~N(μ,2σ).显然f(x)≥0, 下面来证明1d )(=⎰+∞∞-x x f令t x =-σμ/)(, 得到f (x )的图形:,.dx edx et x 22)(2222121-∞+∞---∞+∞-⎰⎰=πσπσμ.1d 21d 21)11.4(π2d d e,,d d ,de 22)(20222/)(22/2222222======⎰⎰⎰⎰⎰⎰⎰∞∞--∞∞---∞-+∞∞-+∞∞-+-∞∞--x ex e r r I u t e I t I t x r u ttπσπθσμπ于是得转换为极坐标则有记f(x)具有的性质:（1）.曲线关于x=μ对称. 这表明对于任意h>0有P{μ-h<X ≤μ}=P{μ<X ≤μ+h}.（2）.当x=μ时取到最大值.π21)(σμ=f x 离μ越远, f(x)的值越小. 这表明对于同样长度的区间, 当区间离μ越远, X 落在这个区间上的概率越小。

连续型分布函数连续型分布函数是概率论和数理统计中的一个重要概念，它描述了一个随机变量取某个值以下的概率。

在实际问题中，我们经常需要对连续型随机变量进行概率分析和统计推断。

本文将介绍连续型分布函数的定义、性质和常见的几种连续型分布函数。

一、连续型分布函数的定义连续型分布函数是指一个随机变量的取值范围是实数集，并且每一个实数都对应一个概率。

它可以表示为F(x)，表示随机变量取值小于等于x的概率，即P(X≤x)。

1. F(x)是一个非递减的函数，即对于任意的a≤b，有F(a)≤F(b)；2. F(x)的取值范围是[0,1]，即0≤F(x)≤1；3. 当x趋于负无穷时，F(x)趋于0；当x趋于正无穷时，F(x)趋于1；4. F(x)是右连续的，即对于任意的x，有F(x+)=F(x)；5. F(x)的变化是分段的，即在每个区间上是一个线性函数。

三、常见的连续型分布函数1. 均匀分布函数（Uniform Distribution Function）均匀分布函数是指随机变量在一定区间上的取值是等可能的，即每个取值的概率相等。

它的分布函数为：F(x) = (x-a)/(b-a)，其中a为区间下限，b为区间上限。

2. 正态分布函数（Normal Distribution Function）正态分布函数是指随机变量满足正态分布的情况，也称为高斯分布。

它的分布函数没有解析表达式，通常用标准正态分布函数进行近似计算。

3. 指数分布函数（Exponential Distribution Function）指数分布函数是指随机变量满足指数分布的情况，它描述了事件发生的时间间隔。

它的分布函数为：F(x) = 1 - e^(-λx)，其中λ为事件发生的速率参数。

4. 伽玛分布函数（Gamma Distribution Function）伽玛分布函数是指随机变量满足伽玛分布的情况，它常用于描述等待时间或寿命分布。

它的分布函数没有解析表达式，通常使用伽玛函数进行计算。