下载文档原格式
停留时间分布综合实验报告停留时间分布综合实验一、实验目的1.掌握用脉冲示踪法测定停留时间分布及数据处理方法；2.了解和掌握停留时间分布函数的基本原理；3.了解停留时间分布与模型参数的关系；4.了解多级混本实验通过单釜、多釜及管式反应器中停留时间分布的测定， 将数据计算结果用多釜串联模型来定量返混程度，从而认识限制返混的措施死 )()/()(0t c M Q t E ⋅= (2) 其中：Q0主流体体积流量，M 为示踪物量，c(t)为t 时刻流出的示踪剂浓度。
对停留时间分布密度函数E(t)有两个重要概念，数学期望_t 和方差2t σ，它们分别定义为E(t)对原点的一次矩和二次矩。
当实验数据的数量大，且所获样品是瞬间样品，即相应于某时刻t 下的样品，则：∑∑∑∑====-∆∆=∆∆=Ni iAiNi iAii Ni iiNi iiit ct ct tt E t t E t t 1111)()( (3)211221122)()(t t ct ct t t t E t t E tNi iAiNi iAii N i iiNi ii it -∆∆=-∆∆=∑∑∑∑====σ (4)级 21θσ=N (9)三、实验仪器、设备和试剂实验仪器与设备：釜式反应器(两个)、管式反应器（一个）、水泵（一个）、转子流量计，阀门，管线若干，电导率仪三台，分析天平； 实验试剂：饱和KCl 溶液。
四、实验装置原理图1-槽；2－磁力泵；3－调节阀；4－三通阀；5－注射器；6、10、11、16－球阀；五、实验安排5.1实验内容1、安装实验装置。
2、测定不同浓度下KCl电导率的标准曲线（最大值为2mS）。
计算对示踪剂注入量，并根据反应器体积计算KCl溶液的浓度范围是否在可测量范围。
3、选择合适的流量，将平均停留时间保持在10－20min，注入适量的示踪剂，测定单釜不同时间的电导率值，绘制单釜停留时间与电导关系曲线，计算停留时间分布函数及停留时间分布密度函数。
![[讲解]连续流动反应器停留时间分布的测定](https://img.taocdn.com/s1/m/dc3bac3be3bd960590c69ec3d5bbfd0a7956d5bf.png)
连续流动反应器停留时间分布的测定一、实验目的1、了解连续流动反应器内停留时间分布的含义及其产生的原因；2、加深对停留时间分布概念的理解；3、掌握如何应用停留时间分布的测定来描述反应器中的逆向混合情况；4、掌握停留时间分布的测试方法及其结果的处理。
二、实验原理停留时间分布测定所采用的方法主要是示踪响应法。
它的基本思路是：在反应器入口以一定的方式加入示踪剂，然后通过测量反应器出口处示踪剂浓度的变化，间接地描述反应器内流体的停留时间。
常用的示踪剂加入方式有脉冲输入、阶跃输入和周期输入等。
本实验选用的是脉冲输入法。
脉冲输入法是在极短的时间内，将示踪剂从系统的入口处注入注流体，在不影响主流体原有流动特性的情况下随之进入反应器。
与此同时，在反应器出口检测示踪剂浓度c(t)随时间的变化。
整个过程可以用图2形象地描述。
图2 脉冲法测定停留时间分布示意图由概率论知识可知，概率分布密度函数E(t)就是系统的停留时间分布密度函数。
因此，E（t）dt就代表了流体粒子在反应器内停留时间介于t到t+dt之间的概率。
在反应器出口处测得的示踪剂浓度c(t)与时间t的关系曲线叫响应曲线。
由响应曲线就可以计算出E（t）与时间t的关系，并绘出E（t）～t关系曲线。
计算方法是对反应器作示踪剂的物料衡算，即Qc(t)dt=mE(t)dt （1）式中Q表示主流体的流量，m为示踪剂的加入量。
示踪剂的加入量可以用下式计算⎰∞=)(m dt t Qc （2）在Q 值不变的情况下，由（1）式和（2）式求出：⎰=∞)()(t E dtt c t c ）（ （3）关于停留时间分布的另一个统计函数是停留时间分布函数F(t),即dt t E )(t F 0⎰∞=）（ （4）用停留时间分布密度函数E （t ）和停留时间分布函数F （t ）来描述系统的停留时间，给出了很好的统计分布规律。
但是为了比较不同停留时间分布之间的差异，还需要引入另外两个统计特征值，即数学期望和方差。
停留时间分布综合实验报告停留时间分布综合实验一、实验目的1.掌握用脉冲示踪法测定停留时间分布及数据处理方法；2.了解和掌握停留时间分布函数的基本原理；3.了解停留时间分布与模型参数的关系；4.了解多级混本实验通过单釜、多釜及管式反应器中停留时间分布的测定, 将数据计算结果用多釜串联模型来定量返混程度,从而认识限制返混的措施 和釜、管式反应器特性；5.了解和掌握模型参数N 的物理意义及计算方法;二、实验原理在连续流动反应器中,由于反应物料的返混以及在反应器内出现的层流,死角,短路等现象,使得反应物料在反应器中的停留时间有长有短,即形成停留时间分布,影响反应进程和最终结果;测定物料的停留时间分布是描述物料在反应器内的流动特性和进行反应器设计计算的内容之一;停留时间分布可以用停留时间分布密度函数 Et 和停留时间分布函数 Ft 来表示,这两种概率分布之间存在着对应关系,本实验只是用冲脉示踪法来测定 Et,利用其对应关系也可以求出 Ft 来;函数 Et 的定义是：在某一瞬间加入系统一定量示踪物料,该物料中各流体粒子将经过不同的停留时间后依次流出,而停留时间在t,t+dt 间的物料占全部示踪物料的分率为 Etdt;根据定义Et 有归一化性质：0.1`)(0=⎰∞dt t E 1 Et 可以用其他量表示为)()/()(0t c M Q t E ⋅= 2 其中：Q0主流体体积流量,M 为示踪物量,ct 为t 时刻流出的示踪剂浓度;对停留时间分布密度函数Et 有两个重要概念,数学期望_t 和方差2t σ,它们分别定义为Et 对原点的一次矩和二次矩;当实验数据的数量大,且所获样品是瞬间样品,即相应于某时刻t 下的样品,则：∑∑∑∑====-∆∆=∆∆=Ni iAiNi iAii Ni iiN i iiit ct ct tt E t t E t t 1111)()( 3211221122)()(t t ct ct t t t E t t E tNi iAiNi iAii N i iiNi ii it-∆∆=-∆∆=∑∑∑∑====σ 4 式中△ti 是两次取样时间,若等时间间隔取样,2112211t cct cct t Ni AiNi Aii tNi AiNi Aii -==∑∑∑∑====-σ 5对恒容稳定流动系统有： τ==-v V t R6 为了使用方便,常用对比时间τθt=来代换t,经这样变换后,有以下关系：)()(t E E τθ= 7222τσσθt = 8对全混流12=θσ,对活塞流02=θσ,对一般情况102<<θσ;用无因次2θσ来评价反应器内的流动状态比较方便,一般可将实际反应器当做多级串联釜式反应器加以描述,并认为每级为全混流反应釜,各级存料量相等,级间无返混;对多级全混釜有N 为串联全混釜的个数： 21θσ=N 9三、实验仪器、设备和试剂实验仪器与设备：釜式反应器两个、管式反应器一个、水泵一个、转子流量计,阀门,管线若干,电导率仪三台,分析天平； 实验试剂：饱和KCl 溶液;四、实验装置原理图1-槽；2－磁力泵；3－调节阀；4－三通阀；5－注射器；6、五、实验安排实验内容1、安装实验装置;2、测定不同浓度下KCl电导率的标准曲线最大值为2mS;计算对示踪剂注入量,并根据反应器体积计算KCl溶液的浓度范围是否在可测量范围;3、选择合适的流量,将平均停留时间保持在10－20min,注入适量的示踪剂,测定单釜不同时间的电导率值,绘制单釜停留时间与电导关系曲线,计算停留时间分布函数及停留时间分布密度函数;4、选择合适流量,将平均停留时间保持在10－20min,注入适量的示踪剂,测定两釜并联条件下的电导率值,计算并绘制单釜及两釜并联的停留时间与电导关系曲线,计算停留时间分布函数及停留时间分布密度函数;5、按4进行两釜串联实验;6、测定釜式、管式反应器串联的停留时间分布曲线,并计算停留时间分布函数及密度分布函数;7、大型智能仪器的操作使用,用其测量釜式反应器串联的停留时间分布曲线,并计算停留时间分布函数及密度分布函数;实验安排时间实验内容六、数据处理电导率的标准曲线由origin作图,可得到如下：经过线性模拟,我们得到其电导率和浓度之间是线性关系,其相关的数值如下表：从上表中,我们不难发现,电导率和浓度之间的关系的线性关系很强,得到：单釜、不转、流量Q=4L/h由origin作图得到,时间与浓度之间的关系如下图：由上表中的数据,用origin作图并模拟积分得：单釜、中转、流量Q=4L/h由origin 作图得到,时间与浓度之间的关系如下图：62.040.9103517.514396tt 3517.514396910.4056.09496107456258186901.11t )()(910.40s 56.09496107425548.83729)()(t :456258186901.11)(425548.83729)(56.09496107)(origin 22222222020≈====-=-=≈=====⎰⎰⎰⎰⎰⎰⎰∞∞∞∞∞∞∞τσσσθt tdtt c dt t c t dt t c dt t tc dt t c t dt t tc dt t c 无因次方差：对于恒容稳态系统有：平均停留时间；；作图并模拟积分得：由上表中的数据，用单釜、中转、流量Q=6L/h由origin作图得到,时间与浓度之间的关系如下图：71.071.30565936.66429tt 65936.6642971.05353.699037068125591432.612t )()(s71.05353.6990370600551130.84974)()(t :8125591432.612)(00551130.84974)(53.69903706)(origin 222222022020≈====-=-=≈=====⎰⎰⎰⎰⎰⎰⎰∞∞∞∞∞∞∞τσσσθt tdtt c dt t c t dtt c dt t tc dt t c t dt t tc dt t c 无因次方差：对于恒容稳态系统有：平均停留时间；；作图并模拟积分得：由上表中的数据，用单釜、中转、流量Q=8L/h由origin作图得到,时间与浓度之间的关系如下图：双釜串联、都不转、流量Q=4L/h由origin 作图得到,时间与浓度之间的关系如下图：18.029.855347806753.1tt 6753.13478029.8554.26534938252254205416.61t )()(s29.8554.2653493810353648.10380)()(t :252254205416.61)(10353648.10380)(4.26534938)(origin 222222022020≈====-=-=≈=====⎰⎰⎰⎰⎰⎰⎰∞∞∞∞∞∞∞τσσσθt tdtt c dt t c t dtt c dt t tc dt t c t dt t tc dt t c 无因次方差：对于恒容稳态系统有：平均停留时间；；作图并模拟积分得：由上表中的数据，用双釜串联、一釜中转一釜大转、流量Q=2L/h由origin 作图得到,时间与浓度之间的关系如下图：32.047.15040523.715280tt 0523.71528047.15045515.45364336100546033467.8t )()(s47.15045515.453643339672523203.1205)()(t :6100546033467.8)(39672523203.1205)(5515.4536433)(origin 22222222020≈====-=-=≈=====⎰⎰⎰⎰⎰⎰⎰∞∞∞∞∞∞∞τσσσθt tdtt c dt t c t dtt c dt t tc dt t c t dt t tc dt t c 无因次方差：对于恒容稳态系统有：平均停留时间；；作图并模拟积分得：由上表中的数据，用双釜串联、一釜中转一釜大转、流量Q=4L/h由origin作图得到,时间与浓度之间的关系如下图：47.017.9468425.421347tt 8425.42134717.94658.3170245641132510950074.0t )()(s17.94658.31702456028257869.28027)()(t :41132510950074.0)(028257869.28027)(58.31702456)(origin 222222022020≈====-=-=≈=====⎰⎰⎰⎰⎰⎰⎰∞∞∞∞∞∞∞τσσσθt tdtt c dt t c t dtt c dt t tc dt t c t dt t tc dt t c 无因次方差：对于恒容稳态系统有：平均停留时间；；作图并模拟积分得：由上表中的数据，用双釜串联、一釜不转一釜大转、流量Q=6L/h由origin 作图得到,时间与浓度之间的关系如下图：43.095.7340403.230012tt 0403.23001295.734755.35476810620254124047.17t )()(s95.734755.3547681051553935.48509)()(t :620254124047.17)(51553935.48509)(755.35476810)(origin 222222022020≈====-=-=≈=====⎰⎰⎰⎰⎰⎰⎰∞∞∞∞∞∞∞τσσσθt tdtt c dt t c t dtt c dt t tc dt t c t dt t tc dt t c 无因次方差：对于恒容稳态系统有：平均停留时间；；作图并模拟积分得：由上表中的数据，用双釜并连、都不转、流量为4L/h。
停留时间分布综合实验报告停留时间分布综合实验一、实验目的1.掌握用脉冲示踪法测定停留时间分布及数据处理方法；2.了解和掌握停留时间分布函数的基本原理；3.了解停留时间分布与模型参数的关系；4.了解多级混本实验通过单釜、多釜及管式反应器中停留时间分布的测定， 将数据计算结果用多釜串联模型来定量返混程度，从而认识限制返混的措施 和釜、管式反应器特性；5.了解和掌握模型参数N 的物理意义及计算方法。
二、实验原理在连续流动反应器中，由于反应物料的返混以及在反应器内出现的层流，死角，短路等现象，使得反应物料在反应器中的停留时间有长有短，即形成停留时间分布，影响反应进程和最终结果。
测定物料的停留时间分布是描述物料在反应器内的流动特性和进行反应器设计计算的内容之一。
停留时间分布可以用停留时间分布密度函数 E(t)和停留时间分布函数 F(t)来表示，这两种概率分布之间存在着对应关系，本实验只是用冲脉示踪法来测定 E(t)，利用其对应关系也可以求出 F(t)来。
函数 E(t)的定义是：在某一瞬间加入系统一定量示踪物料，该物料中各流体粒子将经过不同的停留时间后依次流出，而停留时间在[t ，t+dt]间的物料占全部示踪物料的分率为 E(t)dt 。
根据定义E(t)有归一化性质：0.1`)(0=⎰∞dt t E (1) E(t)可以用其他量表示为)()/()(0t c M Q t E ⋅= (2) 其中：Q0主流体体积流量，M 为示踪物量，c(t)为t 时刻流出的示踪剂浓度。
对停留时间分布密度函数E(t)有两个重要概念，数学期望_t 和方差2t σ，它们分别定义为E(t)对原点的一次矩和二次矩。
当实验数据的数量大，且所获样品是瞬间样品，即相应于某时刻t 下的样品，则：∑∑∑∑====-∆∆=∆∆=Ni iAiNi iAii Ni iiN i iiit ct ct tt E t t E t t 1111)()( (3)211221122)()(t t ct ct t t t E t t E tNi iAiNi iAii N i iiNi ii it -∆∆=-∆∆=∑∑∑∑====σ (4) 式中△ti 是两次取样时间，若等时间间隔取样，2112211t cct cct t Ni AiNi Aii t Ni AiNi Aii -==∑∑∑∑====-σ (5)对恒容稳定流动系统有： τ==-v V t R(6) 为了使用方便，常用对比时间τθt=来代换t ，经这样变换后，有以下关系：)()(t E E τθ= (7)222τσσθt = (8)对全混流12=θσ，对活塞流02=θσ，对一般情况102<<θσ。
实验三串联流动反应器停留时间分布的测定在连续流动反应器中进行化学反应时，反应进行的程度除了与反应系统本身的性质有关外，还与反应物料在反应器中停留时间长短有密切关系。
停留时间越长，则反应越完全。
停留时间通常是指从流体进入反应器开始，到其离开反应器为止的这一段时间。
显然对流动反应器而言，停留时间不象间歇反应器那样是同一个值，而是存在一个停留时间分布。
造成这一现象的主要原因是流体在反应器内流速分布的不均匀，流体的扩散，以及反应器内的死区等。
停留时间分布的测定不仅广泛应用于化学反应工程及化工分离过程，而且应用于涉及流动过程的其它领域。
它也是反应器设计和实际操作所必不可少的理论依据。
一．实验目的1．通过实验了解停留时间分布测定的基本原理和实验方法。
2．掌握停留时间分布的统计特征值计算方法3．学会用理想反应器的串联模型来描述实验系统的流动特性。
二．实验原理停留时间分布测定所采用的方法主要是示踪响应法。
它的基本思路是：在反应器入口以一定的方式加入示踪剂，然后通过测量反应器出口处示踪剂浓度的变化，间接地描述反应器内流体的停留时间。
常用的示踪剂加入的方式有脉冲输入、阶跃输入和周期输入等。
本实验选用的是脉冲输入法。
脉冲输入法是在极短的时间内，将示踪剂从系统的入口处注入主体流，在不影响主流体原有流动特性的情况下随之进入反应器。
与此同时，在反应器出口检测示踪剂浓度c(t)随时间的变化。
整个过程可以用图３—１（a）形象地描述。
示踪剂检测示踪剂加入Ｑ∞Q（a）脉冲输入法c 0 c 0————————————————C Ct=0 t t(b) 脉冲输入 (c) 出口响应图３－１脉冲法测停留时间分布脉冲输入法测得的停留时间分布代表了物料在反应器中的停留时间分布密度即E(t)。
若加入示踪剂后混合流体的流率为Q ，出口处示踪剂浓度为C （t ），在dt 时间里示踪剂的流出量为Qc(t)dt ，由E(t)定义知E(t)dt 是出口物料中停留时间在t 与t+dt 之间示踪剂所占分率，若在反应器入口加入示踪剂总量为m 对反应器出口作示踪剂的物料衡算，即Qc(t)dt=mE(t)dt （１） 示踪剂的加入量可以用下式计算m=⎰∞0)(dt t Qc （２） 在Ｑ值不变的情况下，由（１）式和（２）式求出：E (t)=⎰∞0)()(dt t c t c （３） 关于停留时间的另一个统计函数是停留时间分布函数F(t)，即F (t)= ⎰∞0)(dt t E （４）用停留时间分布密度函数E(t)和停留时间分布函数F(t)来描述系统的停留时间，给出了很好的统计分布规律。
实验一连续搅拌釜式反应器停留时间分布的测定一、实验目的(1)加深对停留时间分布概念的理解；(2)掌握测定液相停留时间分布的方法；(3)了解停留时间分布曲线的应用。
(4)了解停留时间分布于多釜串联模型的关系，了解模型参数N的物理意义及计算方法。
(5)了解物料流速及搅拌转速对停留时间分布的影响。
二、实验原理(1)停留时间分布当物料连续流经反应器时，停留时间及停留时间分布是重要概念。
停留时间分布和流动模型密切相关。
流动模型分平推流，全混流与非理想流动三种类型。
对于平推流，流体各质点在反应器内的停留时间均相等，对于全混流，流体各质点在反应器内的停留时间是不一的，在0〜必范围内变化。
对于非理想流动，流体各质点在反应器内的停留时间分布情况介乎于以上两种理想状态之间，总之，无论流动类型如何，都存在停留时间分布与停留时间分布的定量描述问题。
(2)停留时间分布密度函数E(t)停留时间分布密度函数E(t)的定义：当物料以稳定流速流入设备(但不发生化学变化)时，在时间t=0时，于瞬时问dt进入设备的N个流体微元中，具有停留时间为t到(t+dt)之间的流体微元量dN占当初流入量N的分率为E(t)dt,即弋二E(t)dtE(t)定义为停留时间分布密度函数。
由于讨论的前提是稳定流动系统，因此，在不同瞬间同时进入系统的各批N个流体微元均具有相同的停留时间分布密度，显然，流过系统的全部流体，物料停留时间分布密度为同一个E(t)所确定。
根据E(t)定义，它必然具有归一化性质:/E(t)dt=1⑵不同流动类型的E(t)曲线形状如图1所示。
根据E(t)曲线形状，可以定性分析物料在反应器(设备)内停留时间分布。
(3)停留时间分布密度函数E(t)的测定停留时间分布密度函数E(t)的测定，常用的方法是脉冲法。
此法采用的示踪剂，既不与被测流体发生化学反应，又不影响流体流动特性，也就是说，示踪物在反应器(设备)内的停留时间分布与被测流体的停留时间分布相同。
实验一多釜串联连续流动反应器中停留时间分布的测定实验目的：测定多釜串联连续流动反应器中的停留时间分布。
实验原理：多釜串联连续流动反应器是由多个容积相等的釜串联而成的反应器。
在反应过程中，反应物随着流体一起在不同釜内流动。
在不同釜内停留的时间不同，即停留时间分布不同。
停留时间分布的测定可以帮助了解反应器的传质和反应过程。
测定停留时间分布的方法有很多，其中一种是通过追踪单个分子的行踪来测定停留时间分布。
具体原理如下：追踪单个分子实验的基本原理是在反应混合物中加入极微小的标记剂，使得反应混合物中只有非常少量的分子带有标记剂。
标记剂可以是荧光分子、放射性同位素或其他具有特殊性质的分子。
在反应过程中，标记剂所在的分子会随着流体在不同的釜内流动，并在其中停留不同的时间。
通过对标记剂的跟踪，可以测定不同停留时间釜内的标记分子数目，进而得到停留时间分布。
实验步骤：1.准备多釜串联反应器，并安装流速计和采样管。
2.将标记剂加入反应混合物中。
3.将反应混合物注入反应器，开始反应。
4.在不同时间内采取样品，对样品中的标记分子进行计数和浓度测定，得到停留时间分布。
实验注意事项：1.要使用极微小的标记剂，确保标记分子的数量足够少，否则会影响停留时间分布的测定结果。
2.要准确地测定标记分子的浓度，可以使用荧光探测器、放射性探测器等设备进行测定。
3.要保证反应混合物的均匀性，避免反应过程中发生不均匀的分布，影响测定结果。
实验结果：通过单个分子追踪实验，可以得到多釜串联流动反应器中的停留时间分布。
停留时间分布的形状和峰值位置可以反映反应器的传质效率和反应速率等重要参数。
对于反应器的设计和优化，停留时间分布的测定是非常重要的。
反应工程实验实验 1 连续搅拌釜式反应器液体停留时间分布及其流动模型的测定⑴ 何谓返混？答：返混是指不同的停留时间的微团之间的混合。
⑵ 返混的起因是什么？答：器内反应流体的流动状态、混合状态以及器内的传热性能等。
⑶ 限制返混的措施有那些？答：器内反应流体的流动状态和混合状态的复杂性，反应流体在反应器内浓度、温度和速度的分布造成返混。
⑷ 测定停留时间分布的方法有那些？答：脉冲法、阶跃法、周期示踪法和随机输入示踪法⑸ 本实验采用哪种方法？答：脉冲示踪法。
⑹ 何谓示踪剂？答：平推流和理想混合流。
⑺ 对于示踪剂有什么要求？答：反应器出口的反应物料的各质点具有不同的停留时间。
⑻ 本实验采用什么示踪剂？答：饱和KCL溶液。
⑼ 为什么说返混与停留时间分布不是一一对应的？答：器内物料的返混会导致各种不同的停留时间分布而有停留时间分布的反应器，器内未必一定有返混存在。
⑽ 为什么可以通过测定停留时间分布来研究返混？答：在定常态下的连续流动的系统中，相对于某瞬间的流入反应器的流体，在反应器出口流体的质点中在器内停留了⊿t的流体的质点所占的分率。
⑾ 模型参数与实验中反应釜的个数有何不同？答：多级全混流模型。
⑿ 模型参数与实验中反应釜的个数为什么不同？答：不同。
模型参数N的数值可检验理想流动反应器和度量非理想流动反应器的返混程度。
当实验测得模型参数N值与实际反应器的釜数相近时，则该反应器达到了理想的全混流模型。
若实际反应器的流动状况偏离了理想流动模型，则可用多级全混流模型来模拟其返混情况，用其模型参数N值来定量表征返混程度。
⒀ 如何保证各釜有效容积相等？答：要保持水的流量和釜内波面高度稳定。
⒁ 本次实验用什么来测电导率？如何清理？答：铂黑电极。
用丙酮清洗。
⒂ 实验过程中如何保持操作条件的恒定和测定仪器的稳定？答：每次实验前，需检查校正电导率仪指针的零点和满量程；保持电极插头洁净，用最好用丙酮擦拭干净；防止电极上气泡的形成，一旦有气泡必须及时清除(放水控干)。
停留时间分布的测定一、实验目的1. 了解利用电导率测定停留时间分布的基本原理和实验方法；2. 掌握停留时间分布的统计特征值的计算方法；3. 了解学会用理想反应器串联模型来描述实验系统的流动特性。
二、实验原理停留时间分布测定所采用的方法主要是示踪响应法。
它的基本思路是：在反应器入口以一定的方式加入示踪剂，然后通过测量反应器出口处示踪剂浓度的变化，间接地描述反应器内流体的停留时间。
常用的示踪剂加入的方式有脉冲输入、阶跃输入和周期输入等。
本实验选用的是脉冲输入法。
脉冲输入法是在极短的时间内，将示踪剂从系统的入口处注入主体流，在不影响主流体原有流动特性的情况口检测示踪剂浓度c(t)随时间的变化。
整个过程可以Ｑ(a) 脉冲输入法c0C C(b) 脉冲输入(c) 出口响应图1 脉冲法测停留时间分布脉冲输入法测得的停留时间分布代表了物料在反应器中的停留时间分布密度即E(t)。
若加入示踪剂后混合流体的流率为Q，出口处示踪剂浓度为C（t），在dt时间里示踪剂的流出量为Qc(t)dt，由E(t)定义知E(t)dt是出口物料中停留时间在t与t+dt之间示踪剂所占分率，若在反应器入口加入示踪剂总量为m对反应器出口作示踪剂的物料衡算，即（１）示踪剂的加入量可以用下式计算（２）在Ｑ值不变的情况下，由（１）式和（２）式求出：（３） 关于停留时间的另一个统计函数是停留时间分布函数F(t)，即（４） 用停留时间分布密度函数E(t)和停留时间分布函数F (t)来描述系统的停留时间，给出了很好的统计分布规律。
但是为了比较不同停留时间分布之间的差异，还需要引入另外两个统计特征值，即数学期望和方差。
数学期望对停留时间分布而言就是平均停留时间_t ，即（５） 方差是和理想反应器模型关系密切的参数，它的定义是：（６） 若采用无因次方差则有2Θσ2Θσ_2/t i σ=2对活塞流反应器02=Θσ,而对全混流反应器12=Θσ;对介于上述两种理想反应器之间的非理想反应器可以用多釜串联模型描述。
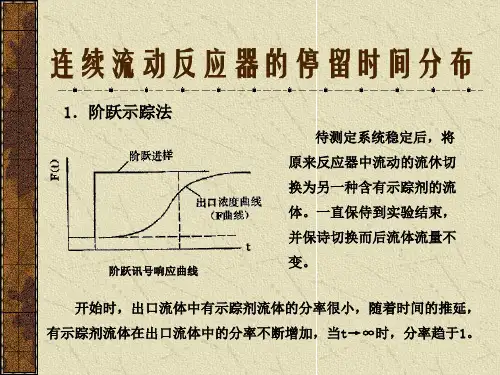
阶跃示踪法测定停留时间分布对应曲线
引言
阶跃示踪法，也称为跳变跟踪法，是一种比较新的测定系统停留时间
分布的方法。
法仅求出停留时间分布的各种累积分布函数以及其对应曲线。
它是一种有效的物理和工程上的解决方案，可以用来提供更精确的数据，
以用来等同地对系统进行诊断、控制以及预测。
技术原理
阶跃示踪法是一种非常简单的方法，只有两步技术原理：查询处理器
停留时间间隔和计算累积分布函数。
首先，通过重复查询处理器的状态，
收集各个时间间隔内的停留时间数据；其次，根据收集到的停留时间数据，根据指数衰减函数对每一时间间隔内停留时间的频率进行累累积，就可以
求出累积分布函数以及其对应的曲线。
技术应用
该技术的技术应用非常广泛，主要应用于电子书、电子杂志等文件制
作和发布中，以及例如计算机网络数据传输、处理器的优化及性能评估等
方面的应用。
因为它可以比较准确的测定系统停留时间分布，有助于文件
或数据的传输和处理过程的检测和改进，并以此提高该过程的性能和效率。
缺点
虽然阶跃示踪法是一种很有用的技术，但它也有一些缺点：
首先，它只能测量系统的停留时间分布，无法测量系统的存取时间分布。
其次，它需要大量的空间来存储测量结果，环境也很重要；另外，它的测量时间也比较长，耗费大量的时间来收集和计算数据。
总结
总之，阶跃示踪法是一种有效的测定系统停留时间分布的技术，它可以有效帮助我们完成各种文件发布和数据传输处理任务，但仍然存在一些缺点。
如果想更好的测量系统性能，仍然需要进一步改进该方法以获得更准确的数据。
CEA-R04型连续搅拌釜式反应器液体停留时间分布仪说明书一、用途与特点CEA－R04型搅拌釜式反应器液体停留时间分布实验仪，适合于设有化学、应用化学、化学工程和轻工等专业的各级各类学校，用于化工基础和化学反应工程的教学实验。
本仪器是经历多年研究和改进，最新设计制造的一种新型实验仪器。
它由三个搅拌釜反应器串联组合而成，并采用了微型计算机联作操作。
反应器主体采用了透明结构，利于学生观察搅拌釜状况，达到良好教学目的，设备结构合理，美观耐用，性能稳定可靠。
本实验仪器可供实验的主要内容：（1）观察和了解连续搅拌釜式反应器的结构、流程及其操作状况。
（2）利用脉冲激发——响应技术测定液体通过单级搅拌釜式反应器和二级或三级串联搅拌釜式反应器的停留时分布。
（3）确定反应器达到理想流动时的操作条件，或在非理想流动状况下模型参数。
二、技术指标（1）外形尺寸：1200mm（W）×420mm（D）×1000（H）（2）操作压力：常压（3）操作温度：室温（4）液体流量：6—60L·h1-（5）搅拌转速：100—600r·min1-（连续可调）（6）数据采集频率：10次·秒1-三、主要设备及其规格（1）搅拌釜式反应器3个反应器容积：1.51直径：100mm高度：200mm 搅拌器驱动方式：电机驱动直流电机转速：0-600r·min1-功率：50W（2）检测与控制器1台数字电导率检测仪0－104μS·cm1-转速调节与测量仪100—600r·min1-（连续可调数字显示）（3）液体（水）稳压与调节系统1套贮水槽：20L水泵：1.25m3h1-转子流量计：6－60 l·h1-（水）（4）电导电极：铂黑电极1套（5）实验数据采集和处理软件1套主要配套设备及规格（用户自理）（1）带有232接口微型计算机1台四、装置流程与使用方法本仪器的装置流程如图1所示。
实验二 连续搅拌釜式反应器 液体停留时间分布及其流动模型的测定一、实验目的当流体连续流过搅拌釜式反应器时，由于各种原因造成物料质点在反应器内停留不一定完全相同，因此形成不同的停留时间分布。
不同停留时间分布直接影响反应的结果(如反应的最终转化率可能不同)。
单级连续搅拌釜式反应器的理想流动模型为全混流模型，而实际反应器是否达到理想流动模型，需要通过实验来检验。
非理想流动反应器的流动模型也需要通过实验来确定。
多级连续搅拌釜式反应器的流动特性和流动模型也都需要通过实验进行研究。
连续流动的搅拌釜式反应器的流动特性的研究和流动模型的确立，一般采用实验测定停留时间分布的方法。
实验测定停留时间分布的方法常用的脉冲激发——响应技术。
本实验采用脉冲激发的方法测定液体(水)连续流过搅拌釜式反应器的停留时间分布曲线。
由此了解反应器的流动特性和流动模型。
通过本实验，使实验者观察和了解连续流动的单级、二级串联或三级串联搅拌釜式反应器的结构、流程和操作方法；掌握一种测定停留时间分布的实验技术；初步掌握液体连续流过搅拌釜式反应器的流动模型的检验和模型参数的测定方法。
无疑，通过实验对于停留时间分布与返混的概念，以及有关流动特性数学模型的概念、原理和研究方法会有更具体的了解和更加深入的理解。
二、实验原理流体流经反应器的流动状况，可以采用激发—响应技术，通过实验测定停留时间分布的方法，以一定的表达方式加以描述。
本实验采用的脉冲激发方法是在设备入口处，向主体流体瞬时注入少量示踪剂，与此同时在设备出口处检测示踪剂的浓度)(t c 随时间t 的变化关系数据或变化关系曲线。
由实验测得的t t c -)(变化关系曲线可以直接转换为停留时间分布密度t t E -)(随时间t 的关系曲线。
由实验测得的t t E -)(曲线的图像，可以定性判断流体流经反应器的流动状况。
由实验测得全混流反应器和多级串联全混流反应器的t t E -)(曲线的典型图像如图1所示。
