当前位置：文档之家 › 激光原理第二章2.1-2.5

激光原理第二章2.1-2.5

  • 格式：ppt
  • 大小：1.53 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

激光原理与技术：第二章

激光原理与技术：第二章
件，大多数情况下，孔径是激活物质的两个端 面，但一些激光器中会另外放置元件以限制光 束为理想的形状。
➢光学谐振腔的种类：
谐振腔的开放程度: 闭腔、开腔、波导腔 开腔通常可以分为: 稳定腔、非稳定腔、临界腔 反射镜形状: 球面腔与非球面腔，端面反射腔与分
布反馈腔 反射镜的多少: 两镜腔与多镜腔（折叠腔、环形
r00
T
r00
共轴球面镜腔 往返传输矩阵：
L A 1
f2
C
1 f1
1 f2
1
L f1
B L 2
L f2
D
L f1
1
L f1
1
L f2
•往返矩阵T与光线的初始坐标参数r0和
轴光线在腔内往返传播的行为
0
无关，因而它可以描述任意近
例：
L 3 R2 4
g1
1
L R1
1;
g2
1
L R2
1 4
§2.1.3. 光学谐振腔的损耗，Q值及线宽
损耗的大小是评价谐振腔的一个重要指标，在激光振荡中， 光腔的损耗决定了振荡的阈值和激光的输出能量，也是腔 模理论的重要研究课题
➢光腔的损耗：
1. 几何损耗
选择性损耗、对不同模式，损耗不同
2. 衍射损耗 3. 腔镜反射不完全引起的损耗
非选择性损耗
4. 腔内介质不均匀引起的损耗
Q 2v R
Q
2v
R
2v
L'
C
❖腔的品质因数Q值是衡量腔质量的一个重要的物理量，它
表征腔的储能及损耗特征。
总之，腔平均单程损耗因子、光子寿命、与腔的品质因数三个 物理量之间是关联的，腔平均单程损耗因子越小，光子寿命越 长，腔的品质因数越高。

第2章激光基本原理优秀PPT

第2章激光基本原理优秀PPT
在给定条件下求解麦克斯韦方程，得到一序列的解，每个解
都表示光场的一种分布，也就是光波的一种模式，或称一种
波型。
讨论光在如图2.1所示的体积为V的各向同性介质中运动时，
可能存在的模式数目
分三种情况讨论
1.在偏振和频率都是一定的情况下，因传播方向不同，
可能存在的模式数目。
对应于从尺度为d的光源发出的波长为λ的光，因衍射限制，在R处

h
Px Py P

(2-20)
c
因为∆很小，故有 ≈ ，所以，∆PZ 的测不准量主要来自频率的测不准量

h
Pz P
(2-21)
c
根据前述的光子态在相空间的体积为 xyzP P P
x
y
z
h
3
h3
c3
xyz
2
VCS
来确定光子的一种状态
在六维相空间（x，y，z，Px，Py，Pz）内，光子的一种状态
所对应的相空间体积元为
上述相空间体积元称为相格。
相格是相空间中用任何实验所能分辨的最小尺度。
光子以动量Px，Py，Pz组成的动量空间内，它的一种运动状态占
据动量空间的体积元
由（2-13）得
上式中的V= ΔxΔyΔz是光子运动的体积。
第2章激光基本原理
【学习目标】
掌握有关激光的基本原理及研究有
关问题的思路和方法，了解激光器
的基本结构、各种类型激光器
【学习要求】
☞ 熟悉光子的基本性质，光波模式、光子态、相
干体积、相格等概念，理解光的相干性
☞ 掌握光的受激辐射概念、爱因斯坦系数之间关
系，理解光的自激振荡，掌握激光振荡条件

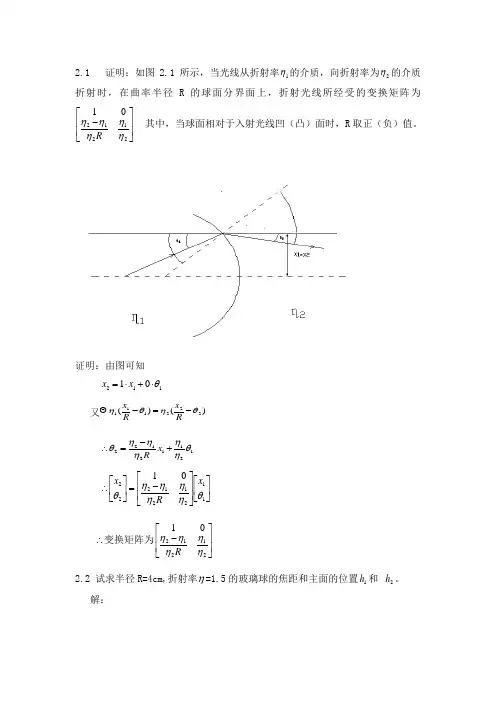
激光原理第二章习题答案

激光原理第二章习题答案

2.1 证明：如图2.1所示，当光线从折射率1η的介质，向折射率为2η的介质折射时，在曲率半径R 的球面分界面上，折射光线所经受的变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 其中，当球面相对于入射光线凹（凸）面时，R 取正（负）值。

证明：由图可知 11201θ⋅+⋅=x x 又)()(222111θηθη-=-RxR x 21121122x R ηηηθθηη-∴=+ ⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∴11212122201θηηηηηθx Rx ∴变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 2.2 试求半径R=4cm,折射率η=1.5的玻璃球的焦距和主面的位置1h 和2h 。

解：变换矩阵⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=2112121221210110101n n R n n n l n n R n n n M 把11=n ，5.12=n ，cm R R 421=-=，cm l 8=代入，可得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡⨯-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=3531316355.1145.115.10110815.145.1101M )(12f h A -=, f C 1-=, )(11f h D -= 求得 mm f 30-= mm h 201= mm h 202=2.3 焦距1f =5cm 和2f =-10c=m 的两个透镜相距5cm 。

第一个透镜前表面和第二个透镜后表面为参考平面的系统，其等效焦距为多少？焦点和主平面位置在何处？距1f 前表面20cm 处放置高为10cm 的物体，能在2f 后多远地方成像？像高为多少？ 解：（1）2110101010********1131101011110552A B L M CD f f ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)(12f h A -=, f C 1-=, )(11f h D -=，求得cm f 5-= cm h 5.21= cm h 52-=第一个透镜前表面与前主面的距离为2.5cm ，第二个透镜后表面与后主面的距离为-5cm,前主面离焦点的距离为-5cm ，） （2）21201011===l x θ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡45252110235150235150111122θθθx x D C B A xcm l cm x 2,5.222-==（距2f 后表面-2cm ）2.4 一块折射率为η，厚度为d 的介质放在空气中，其两界面分别为曲率半径等于R 的凹球面和平面，光线入射到凹球面上。

第2章陈鹤鸣激光原理

第2章陈鹤鸣激光原理

1
Ani
如果同时存在非辐射跃迁，则寿命也缩短。
2.2.2 受激吸收
E2
h
E1
吸收前
吸收后
h E2 E1
受激吸收跃迁几率：
W12

( dn12 dt
)st
1 n1
W12 B12
与原子本身性质和辐射场能量密度有关
B12 ：受激吸收跃迁爱因斯坦系数
只与原子本身性质有关
2.2.3 受激辐射
对激光工作物质的要求：尽可能在其工作粒子的特定能级 间实现较大程度的粒子数反转；使这种反转在整个激光发射 作用过程中尽可能有效地保持下去。
2.4.3 泵浦源
作用：对激光工作物质进行激励，将激活粒子 从基态抽
运到高能级，以实现粒子数反转。
泵浦方式：
气体激光器气体放电激励示意图
1. 光泵浦； 2. 气体放电激励 3. 化学激励 4. 电子注入
I 0 —— z 0 处的初始光强
②大信号增益系数：
g0 g(I)
I(z) 1
Is
I s ——饱和光强（决定于增益介质的性质）
I(z) Is
g(I) g0
进一步讨论可知，增益系数还与光的频率有关。
（2） 损耗系数
dI(z) 1
dz I(z)
损耗因素：衍射、散射、透射、吸 收等
激发态
非辐射跃迁
泵浦
E2
亚稳态 （激光上能级）
产生激光
E1
基态 （激光下能级）
红宝石中铬离子能级图
Energy
E3
Laser Radiation
E2 Fast transition
Abs. E1
N

激光原理第二章答案解析

激光原理第二章答案解析

第二章 开放式光腔与高斯光束1. 证明如图2.1所示傍轴光线进入平面介质界面的光线变换矩阵为121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=，写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 证明光线通过图2.2所示厚度为d 的平行平面介质的光线变换矩阵为1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，入射光线首先经界面1折射，然后在介质2中自由传播横向距离d ，最后经界面2折射后出射。

根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。

3．试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证：设光线在球面镜腔内的往返情况如下图所示：其往返矩阵为：由于是共焦腔，则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。

光的受激辐射 激光原理及应用 [电子教案]电子

光的受激辐射 激光原理及应用 [电子教案]电子

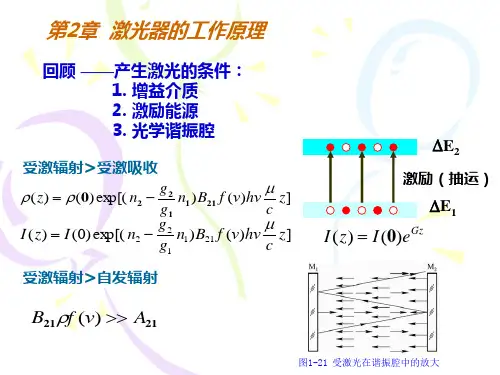
光的受激辐射激光原理及应用第一章：激光概述1.1 激光的定义激光的中文全称：Light Amplification Stimulated Emission of Radiation 激光的特点：相干性好、平行度好、亮度高、单色性好1.2 激光的产生原理受激辐射：外来的光子与一个束缚电子发生能量交换，使电子从较低能级跃迁到较高能级，成为激发态电子。

激发态电子回到较低能级时，会释放出一个与外来光子频率、相位、偏振方向相同的光子，这就是受激辐射。

激光的放大过程：受激辐射产生的光子与入射光子具有相同的频率和相位，导致更多的束缚电子发生受激辐射，从而实现光的放大。

1.3 激光的应用领域科研领域：光谱分析、激光干涉、激光雷达等。

工业领域：激光切割、激光焊接、激光打标等。

医疗领域：激光手术、激光治疗、激光美容等。

生活领域：激光打印、激光投影、激光视盘等。

第二章：激光器的基本原理2.1 激光器的组成激光介质：产生激光的物质，如半导体、气体、固体等。

泵浦源：提供能量，使激光介质中的电子发生跃迁。

光学谐振腔：限制激光的传播方向，增强激光的放大效果。

输出耦合器：将激光输出到外部。

2.2 激光的产生过程泵浦源激发激光介质，使电子从基态跃迁到激发态。

激发态电子回到基态时，发生受激辐射，产生激光。

激光在光学谐振腔内多次反射，实现光的放大。

输出耦合器将激光输出到外部。

2.3 激光器的类型及特点气体激光器：采用气体作为激光介质，如二氧化碳激光器、氦氖激光器等。

固体激光器：采用固体材料作为激光介质，如钕激光器、钇铝石榴石激光器等。

半导体激光器：采用半导体材料作为激光介质，如激光二极管等。

光纤激光器：采用光纤作为激光介质，具有高亮度、低阈值等优点。

第三章：激光的性质与应用3.1 激光的相干性3.2 激光的平行度3.3 激光的亮度亮度高的特点：可用于激光投影、激光显示等。

3.4 激光的单色性3.5 激光的应用实例激光切割：用于金属和非金属材料的切割加工。

激光原理与技术完整ppt课件

激光原理与技术完整ppt课件

够存在于腔内的驻波(以某一波矢k为标志)称为电磁被的模式或光波模。一种模式是电
磁波运动的一种类型，不同模式以不同的k区分。同时，考虑到电磁波的两种独立的偏振，
同一波矢k对应着两个具有不同偏振方向的模。
精选ppt
9
下面求解空腔v内的模式数目。设空腔为V=ΔxΔyΔz的立方体，则沿三个
坐标轴方向传播的波分别应满足的驻波条件为
第八章 激光器特性的控制和改善
8.1 模式选择 8.2 频率稳定 8.3 Q调制 8.4 注入锁定 8.5 锁模
精选ppt
5
第九章 激光器件
9.1 固体激光器 9.2 气体激光器 9.3 半导体激光器 9.4 染料激光器
精选ppt
6
第一章 激光的基本原理
本章概激光器基本原理。讨论的重点是光的相干性和光波模式的联系、光的受激辐
（1.1.4）
式中E0为光波电场的振幅矢量，ν为单色平面波的频率，r为空间位置坐标矢量，k为波
矢。而麦克斯韦方程的通解可表为一系列单色平面波的线性叠加。
在自由空间，具有任意波矢k的单色平面波都可以存在。但在一个有边界条件限制的
空间V(例如谐振腔)内，只能存在一系列独立的具有特定波矢k的平面单色驻波。这种能
第六章 激光器的放大特性
6.1 激光放大器的分类 6.2 均匀激励连续激光放大器的增益特性 6.3 纵向光均匀激励连续激光放大器
的增益特性 6.4 脉冲激光放大器的增益特性 6.5 放大的自发辐射（ASE） 6.6 光放大的噪声
精选ppt
4
第七章 激光振荡的半经典理论
7.1 激光振荡的自洽方程组 7.2 原子系统的电偶级距 7.3 密度距阵
二、光波模式和光子状态相格 从上面的叙述已经可以看出，按照量子电动力学概念，光波的模式和光子的状态是等

激光原理第二章 激光器的工作原理

激光原理第二章 激光器的工作原理

可以证明，在对称共焦腔内，任意傍轴光线可往返多次
而不横向逸出，而且经两次往返后即可自行闭合。
整个稳定球面腔的模式理论都可以建立在共焦腔振荡理 论的基础上，因此，对称共焦腔是最重要和最具有代表性的 一种稳定腔。
3.平行平面腔——由两个平面反射镜组成的共轴谐振腔
R1=R2=∞，g1=g2=1， g1 g2=1
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔，由一个凹面镜和一个凸面镜组成，对应图中5区和6区。
➢ (g1>1,g2<1; g2>1,g1<1)
➢共焦腔，R1＝R2＝L，因而，g1=0，g2=0，对应图中的坐标原点。(特殊的稳定腔) ➢半共焦腔，由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点g1=1，g2=1/2
1. 工作物质 2. 激励能源
受激辐射>受激吸收
3. 光学谐振腔
受激辐射>自发辐射
是否只要具备激励能源和工作物质就一定可以实 现粒子数反转？ 粒子数反转和什么因素有关？
速率方程方法: 量子理论的一种简化形式
——速率方程理论：把光频电磁场看成量子化的光子，把 物质体系描述成具有量子化能级的粒子体系。
(三)临界腔: g1 g2 = 0 , g1 g2= 1
临界腔属于一种极限情况,其稳定性视不同的腔而不同. 在谐振理论研究和实际应用中,临界腔具有非常重要的意义.
1.对称共焦腔——腔中心是两镜公共焦 点且：
R1=L
R2=L
R1= R2= R = L=2F F——二镜焦距
F
L
∵ g1 = g2 = 0 ∴ g1 g2 = 0
简化前提: 忽略量子化辐射场的位相特性及光子数的起伏特 性
优点: 形式特别简单, 且可给出激光的强度特性，并粗略描 述烧孔、兰姆凹陷、多模竞争等效应

激光原理第2章

激光原理第2章

初态： 初态：激发态原子
终态： 终态：基态原子
E2
外来光子 hν = E2 – E1
发射光子 hν = E2 – E1
E1 特点： 才能引起受激辐射； 特点：只有外来光子能量为 hv =E2-E1才能引起受激辐射； 受激辐射的光子与外来光子的特性完全相同， 受激辐射的光子与外来光子的特性完全相同，即具有相同的 频率、偏振方向、传播方向以及相同的位相；是相干光。 频率、偏振方向、传播方向以及相同的位相；是相干光。 受激辐射是激光器的物理基础
爱因斯坦A 5、 爱因斯坦A、B系数关系
在光和原子相互作用达到动平衡的条件下， (1) 在光和原子相互作用达到动平衡的条件下，
自发辐射、 自发辐射、受激辐射和受激吸收间关系
A21n2dt + B21ρ ν n2dt = B12 ρ ν n1dt
自发辐射光子数 受激辐射光子数 受激吸收光子数
n2 B12 ρ v = n1 A21 + B21ρ v
的光波， 的连续功率， 2、某激光器，输出波长500nm的光波，输出 某激光器，输出波长 的光波 输出1W的连续功率， 的连续功率 问每秒从激光上能级向下能级跃迁的粒子数是多少？ 问每秒从激光上能级向下能级跃迁的粒子数是多少？
2.3
光的受激辐射
1900年 1900年，普朗克利用辐射量子化假 设成功解释黑体辐射分布规律 1913年 1913年，波尔提出原子中电子运动状 态量子化假设
（2）自发辐射跃迁几率 设t 时刻 ，体系处于E2 的总粒子数密度为 n2(t)，从t ～t + dt 体系处于 正比于n ： 时间间隔内自发辐射粒子数密度 dn21 正比于 2(t)：
− dn2 = A21n2 (t )dt

周版激光原理课件第二章

周版激光原理课件第二章

数为：
P
nVd
8 2
c3
Vd
由此关系知，只能压缩V，但是不现实。从而提出开式腔
（无侧壁的封闭腔）。从发散角来看，封闭时为2 ，而
开式时为
a
2
L
压缩倍数为
2
/
a L
2
• 但是，我们知道开式腔是无侧壁的封闭 腔，那么内部会不会有稳定的电磁波存 在？如何求出该电磁波？
§ 2.1光腔理论的一般问题
(t
z
)
A2
A0
cos 2
(t
z
)
总波为二者叠加：
A
A1
A2
2 A0
cos
2
z
cost
稳定波存在必须满足驻波条件：
一维： L q
2
与谐振条件等价
从波动理论知：驻波是稳定存在的波。满足驻波条件的 那些光波称之为光腔的纵模，q为波节数，一般很大。一般 把由整数q所表征的腔内的纵向场分布称为腔的纵模。其特 点是：在腔的横截面内场分布是均匀的，而沿腔的轴线方向 形成驻波，驻波的波节数由q来决定。
共轴
球面 R1
共轴 R2
2. 开放式: 除二镜外其余部分开放 共轴: 二镜共轴 球面腔: 二镜都是球面反射镜(球面镜)
三.光腔按几何损耗(几何反射逸出)的分类:
稳定腔 (光腔中存在着伴轴模,它可在腔内多次传播而不逸出腔外) 光腔 临界腔 (几何光学损耗介乎上二者之间)
非稳腔 (伴轴模在腔内经有限数往返必定由侧面逸出腔外,有很高的
a
在这种条件下，可认为均匀平面波是F-P谐振腔内的最低损 耗模，从而为F-P谐振腔的模式提供一种粗略的，也是有用 的形象。
所以考虑均匀平面波在F-P谐振腔内沿轴线方向往返传播的 情形

激光原理第二章ppt课件

激光原理第二章ppt课件

篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
四、光腔的损耗－－光子在腔内的平均寿命
四、光腔的损耗
损耗的大小是评价谐振腔的一个重要指标，（与激 光阈值相关）本小节对无源、开腔的损耗进行分析。
• 开腔的损耗及其描述 • 光子在腔内的平均寿命 • 无源谐振腔的Q值 • 无源腔的本征振荡模式带宽 • 损耗计算举例
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
四、光腔的损耗－－开腔的损耗及其描述
2、平均单程损耗因子：
•定义：
I1 I0e2
若有多种损耗：
1 ln I0 2 I1
(与1-91比较)
n
i 12n
i
I1I0e 21e 22I0e 2
三、光腔的纵模－－多纵模振荡
1、腔内存在模式要形成稳定的振荡，还必须满足自激振荡
条件：单程小信号G0l增益大于单程损耗δ，即：G0l
2、如果以△νT表示增益曲线高于阈值部分的频带宽度，则 可能同时振荡的纵模数为：
讨论：
q [T ] 1 q
•
当 T q
1，激光器中至少有两个以上的纵模振荡。即多纵
§2.1 光腔理论的一般问题
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
一、光腔的构成与分类

激光原理(第2章)

激光原理(第2章)

三、光腔的损耗 损耗的大小是评价谐振腔的一个重要指标，也是腔模理论的重要研究 课题。光学的损耗大致包括如下几个方面： (1)几何偏折损耗。光线在腔内往返传播时，可能从腔的侧面偏折出 去，这种损耗为几何偏折损耗。其大小首先取决于腔的类型和几何尺寸。 例如，稳定腔内傍抽光线的几何损托应为各零，非稳腔则有较高的几何 损耗。以非稳腔而论，不同几何尺寸的非稳腔，其损耗大小亦各不相同。 其次，几何损耗的高低依模式的不同而异。比如同一平行平面腔内的高 阶横模由于其传播方向与轴的夹角较大，因而其几何损耗也比低阶横模 为大。 (2)衍射损耗。由于腔的反射镜片通常具有有限大小的孔径，因而当 光在镜面上发生衍射时，必将造成一部分能量损失。本节以及本书后面 几章的分析表明，衍射损耗的大小与腔的菲涅耳数 N＝a2/Ll有关，与 腔的几何参数g有关，而且不同横模的衍射损耗也将各不相同。
(3)腔镜反射不完全引起的损耗。它包括镜中的吸收、散射以及镜的 透射损耗，通常的光腔至少有一个反射镜是部分透射的，有时透射率还 可以很高(例如，某些固体激光器的轴输出透射率可以＞ 50％)，另一个 反射镜即使通常称为“全反射”镜，其反射率也不可能做到100％。 (4) 材料中的非激活吸收、散射，腔内插入物 ( 如布儒斯特窗、调 Q 元件、调制器等)所引起的损耗，等等。 上述 (1)(2) 两种损耗常常又称为选择损耗，因为不同模式的几何损 耗与衍射损耗各不相同。 (3)(4)两种损耗称为非选择损耗，在一般情况 下它们对各个模式都一样。 不论损耗的起源如何，我们都可以引进一个“平均单程损耗因子” d 来定量地加以描述。该因子的定义如下：如果初始出发时的光强为 I0， 在无源腔内往返一次后，光强衰减为I1，则
2.1 光腔理论的一般问题
一、光腔的构成和分类
在激活物质的两端恰当地放置两个反射镜片，就构成一个最简单的 光学谐振腔。

周炳琨激光原理第二章习题解答(完整版)

周炳琨激光原理第二章习题解答(完整版)

周炳琨激光原理第二章习题解答（完整版）1.试利用往返矩阵证明对称共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证明：设从镜M 1→M 2→M 1,初始坐标为⎪⎪⎭⎫ ⎝⎛θ00r ，往返一次后坐标变为⎪⎪⎭⎫ ⎝⎛θ11r =T ⎪⎪⎭⎫⎝⎛θ00r ,往返两次后坐标变为⎪⎪⎭⎫⎝⎛θ22r =T •T ⎪⎪⎭⎫ ⎝⎛θ00r 而对称共焦腔，R 1=R 2=L 则A=1-2R L 2=-1 B=2L ⎪⎪⎭⎫⎝⎛-2R L 1=0 C=-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+121R L 21R 2R 2=0 D=-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--211R L 21R L 21R L 2=-1 所以，T=⎪⎪⎭⎫ ⎝⎛--1001故，⎪⎪⎭⎫⎝⎛θ22r =⎪⎪⎭⎫ ⎝⎛--1001⎪⎪⎭⎫ ⎝⎛--1001⎪⎪⎭⎫ ⎝⎛θ00r =⎪⎪⎭⎫⎝⎛θ00r 即，两次往返后自行闭合。

2．试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔的稳定性条件为0<g 1•g 2<1,其中g 1=1-1R L ,g 2=1-2R L（a 对平凹腔：R 2=∞,则g 2=1,0<1-1R L<1，即0<L<R 1 (b)对双凹腔：0<g 1•g 2<1, 0<⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-21R L 1R L 1<1 LR >1，L R >2或L R <1L R <2且LR R >+21(c)对凹凸腔：R 1=1R ,R 2=-2R ,0<⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-21R L 1R L 1<1，L R >1且LR R <-||213．激光器的谐振腔由一面曲率半径为1m 的凸面镜和曲率半径为2m 的凹面镜组成，工作物质长0.5m ，其折射率为1.52，求腔长L 在什么范围内是稳定腔。

激光原理教案第二章

激光原理教案第二章

I m = I0 e
( )
−2δ
'
m
= I 0e
t
−2mδ '
t ,m = 2L '/ c
I (t ) = I 0 e
−
τR
,τ R
L' = δc
激光原理与技术
时间后， 的物理意义: 时间常数τR的物理意义 经过τR时间后， 腔内光强衰减为初始值的1／ 腔内光子数将 腔内光强衰减为初始值的 ／e,腔内光子数将 随时间依指数规律衰减， 随时间依指数规律衰减，到τR 时刻衰减为初 始值1／ 。 愈大， 愈小， 始值 ／e。δ愈大， τR愈小，说明腔的损耗 愈大，腔内光强衰减得愈快。 愈大，腔内光强衰减得愈快。 2．无源谐振腔的Q值 ．无源谐振腔的 值
c ∆ν q = ν q+1 −ν q = , (频率梳） 2L 例：L = 10cm,η = 1气体激光器, ∆ν q = 1.5 ×109 Hz L = 100cm,η = 1气体激光器, ∆ν q = 1.5 ×10 Hz
8
L = 10cm,η = 1.76的红宝石激光器∆ν q = 8.5 ×10 Hz
激光原理与技术
激光原理与技术
光 学 谐 振 腔
闭 腔 稳 定 腔 开 腔 非 稳 腔 临 界 腔 气 体 波 导 腔
激光原理与技术
谐振腔可以按不同的方法可分为： 谐振腔可以按不同的方法可分为： 端面反馈腔与分布反馈腔，球面腔与非球 端面反馈腔与分布反馈腔， 面腔，高损耗腔与低损耗腔， 面腔，高损耗腔与低损耗腔，驻波腔与行波 两镜腔与多镜腔， 腔，两镜腔与多镜腔，简单腔与复合腔 等．本章讨论两镜腔。 二、模的概念、腔与模的一般联系 模的概念、 腔的模式:光学谐振腔内可能存在的电磁场的 腔的模式 光学谐振腔内可能存在的电磁场的 本征态称。 本征态称。场的每一个本征态将具有一定的振 荡频率和一定的空间分布。 荡频率和一定的空间分布。

激光原理 第二章光学谐振腔理论

激光原理 第二章光学谐振腔理论

光学谐振腔一方面具有光学正反馈作用,另一方面 也存在各种损耗。损耗的大小是评价谐振腔质量 的一个重要指标,决定了激光振荡的阈值和激光的 输出能量。本节将分析无源开腔的损耗,并讨论表 征无源腔质量的品质因数Q值及线宽。
一、损耗及其描述 (1)几何偏折损耗: 光线在腔内往返传播时，可能从腔的侧面 偏折出去，我们称这种损耗为几何偏折损 耗。其大小首先取决于腔的类型和几何尺 寸。
概述
3.波动光学分析方法 从波动光学的菲涅耳-基尔霍夫衍射积分理论出发,可以建立 一个描述光学谐振腔模式特性的本征积分方程。 利用该方程原则上可以求得任意光腔的模式,从而得到场的 振幅、相位分布,谐振频率以及衍射损耗等腔模特性。 虽然数学上已严格证明了本征积分方程解的存在性,但只有在 腔镜几何尺寸趋于无穷大的情况下,该积分方程的解析求解 才是可能的。 对于腔镜几何尺寸有限的情况,迄今只对对称共焦腔求出了 解析解。 多数情况下,需要使用近似方法求数值解。虽然衍射积分方 程理论使用了标量场近似,也不涉及电磁波的偏振特性,但与 其他理论相比,仍可认为是一种比较普遍和严格的理论。
第一节 光学谐振腔的基本知识
本节主要讨论光学谐振腔的构成、分类、作用,以及 腔模的概念
光学谐振腔的构成和分类
根据结构、性能和机理等方面的不同,谐振腔有不同 的分类方式。
按能否忽略侧面边界,可将其分为

开腔、 闭腔 气体波导腔
第一节 光学谐振腔的基本知识
开腔而言： 1. 根据腔内傍轴光线几何逸出损耗的高低,又可分为 稳定腔、非稳腔及临界腔; 2. 按照腔镜的形状和结构,可分为球面腔和非球面腔; 3. 就腔内是否插入透镜之类的光学元件,或者是否考 虑腔镜以外的反射表面,可分为简单腔和复合腔; 4. 根据腔中辐射场的特点,可分为驻波腔和行波腔; 5. 从反馈机理的不同,可分为端面反馈腔和分布反馈 腔; 6. 根据构成谐振腔反射镜的个数,可分为两镜腔和多 镜腔等。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

上一页 回首页 下一页 回末页 回目录
2.1.3 稳定图的应用
第 1.制作一个腔长为L的对称稳定腔，反射镜曲率半径的取值范围如何确定？ 二 章 2.给定稳定腔的一块反射镜，要选配另一块反射镜的曲率半径，其取值范围如 激 何确定? 光 器 的 2 3.如果已有两块反射镜，曲率半径分别为R1、R2，欲用它们组成稳定腔，腔长 范围如何确定？ 工 作 1 原 光 理 学
上一页 回首页 下一页 回末页 回目录
2.1.2 共轴球面谐振腔的稳定图及其分类
第 1.常常稳定图来表示共轴球面腔的稳定条件 ，定义：g1 1 L R1 及g2 1 L R2 二 共轴球面谐振腔的稳定性条件可改写为: 0 g1 g 2 1 章 当0 g1 g2 1 时，共轴球面谐振腔为稳定腔 激 光 当 g1 g2 0或g1 g2 1 时，共轴球面谐振腔为非稳腔 器 的 2 当 g1 g2 0或g1 g2 1 时，共轴球面谐振腔为临界腔 工 作 1 原 光 理 学 如图(2-2)所示，图中没有斜线的部分是谐
谐 振 腔 结 构 与 稳 定 性
§ .
图(2-3) 稳定图的应用
上一页 回首页 下一页 回末页 回目录
一、速率方程组
n1 B12 f ( )
n2 B21f ( )
E2
n2 A20 E1 E0
第 1. 图（2.4.1）为简化的四能级图，n0、n1、 二 n2分别为基态、上能级、下能级的粒子数密 R2 n2 A21 章 度；n为单位体积内增益介质的总粒子数， 激 R1、R2分别是激励能源将基态E0上的粒子抽 光 n1 A10 R1 运到E1、E2能级上的速率；则E2能级在单位 器 的 2 时间内增加的粒子数密度为： 图（2.4.1）简化的四能级图 dn2 工 R n A ( n B n B ) f ( ) 2 2 2 2 21 1 12 作 1 dt 原 光 理 学 同理，单位时间内E1能级上增加的粒子数密度为 ： dn1 谐 R1 n2 A21 (n2 B21 n1B12 ) f ( ) n1 A1 振 dt 腔 n0 n1 n2 n
谐 振 腔 结 构 与 稳 定 性
§ .
振腔的稳定工作区，其中包括坐标原点。 图中画有斜线的阴影区为不稳定区，在稳 定区和非稳区的边界上是临界区。对工作 在临界区的腔，只有某些特定的光线才能 在腔内往返而不逸出腔外。
图(2-2) 共轴球面腔的稳定图
上一页 回首页 下一页 回末页 回目录
2.1.2 共轴球面谐振腔的稳定图及其分类
谐 振 腔 结 构 与 稳 定 性
4）依此类推，求出h4，h5，…，可以计算出： 在反射镜M1上，有：h0 < h1 < h3 < …
§ .
A F
A O
B M1 M2 M1 图（2.2.3）(a) 对称共焦腔
B M2 图（2.2.3）(b)共心腔
上一页 回首页 下一页 回末页 回目录
第 二 章 O 激 光 器 的 2 M1 工 图（2.2.3）(c)不稳定凹面腔 作 1 原 光 2.1.4 对称凸面镜腔 理 学
谐 振 腔 结 构 与 稳 定 性
2. 同理，如图（2.2.3）(c)当两块凹面镜的腔长L > 2R的时候就称为了不稳 定腔。
§ .
M2
如图（2.2.4）由两块凸面镜组成的光学谐振腔也是不稳定腔。
图（2.2.4）不稳定凸面腔
上一页 回首页 下一页 回末页 回目录
2.1.5 稳定腔的表达式
第 光学谐振腔的稳定与否是由谐振腔的几何形状决定的。可用一个不等式来表示 二 谐振腔的稳定条件。稳定腔应该满足的条件是hn≤h0，可以证明满足这个不等式 章 的腔必然满足： L L 激 0 (1 ) (1 ) 1 光 R1 R2 器 的 2 2.1.6 稳定图和稳定腔的分类 工 g2 令 g1为横坐标，g 2为纵坐标，由下式可以作出两条 1 作 原 光 双曲线，它们是稳定腔和非稳定腔的分界线。如图 理 学 （2.2.5）所示。把稳定腔大致分为四类，在图上用
谐 振 腔 结 构 与 稳 定 性
2. 如果继续将两反射镜之间的距离拉大，使L>2f，如图（2.2.2）(c)所示。
1）平行光A1A2经M2反射后的光线A2B1经过焦点F，由ΔA2O2F∽ΔB1O1F，
L-f L - 2f h1 h 0 (1 )h 0 h 0 ; 其中＝ 0 f f
谐 振 腔 2.成像公式为: 结 构 与 稳 定 性
§ .
1 1 1 s s f
上一页 回首页 下一页 回末页 回目录
2.1.2 平凹腔 第 二 章 激 光 器 的 2 工 作 1 原 光 理 学
谐 振 腔 结 构 与 稳 定 性
1. 平凹腔是由一块平面镜和一块曲率半径为R的凹面镜组成的光学谐振腔。 图（2.2.2）(a)为半共焦腔，凹面镜的焦点正好落在平面镜上；图（2.2.2） (b)为半共心腔，凹面镜的球心正好落在平面镜上。
谐 Ⅰ、Ⅱ、Ⅲ、Ⅳ标出。 振 L g 1 其中： 腔 1 R1 结 L 构 g2 1 与 R2 稳 L L g g ( 1 ) ( 1 ) 1 1 2 定 R1 R2 性
§ .
Ⅳ A 1Ⅱ Ⅰ Ⅳ Ⅱ ⅢⅠ O 1 B Ⅲ
g1
图（2.2.5）稳定腔图
上一页 回首页 下一页 回末页 回目录
h1 : h0 = (L-f) : f
2）M1的反射光B1B2对M2来说相当于由F在M1中的象B0发出的，即B0O1=L-f， 所以B0到M2的距离sB=B0O2=2L-f，由ΔB0O1B1∽ΔB0O2B2， h2 : h1 = (2L-f) : (L-f)
§ .
h2
3）M2的反射光B2C1将通过B0在M2中的象点B'0，则象距s'B=B'0O2可由成像 2 公式求出。 又由ΔC1B‘0O1∽ΔB2B‘0O2，
在坐标系上，直线线段BOA代表第一类腔(Ⅰ)---对称腔。其特点是：R =R =R。
谐 代表曲率半径小于腔长的非对称腔。其特点： 振 R ≠R2；0＜R1＜L，0＜R2＜L，但必须满足 腔 1 R +R ＞L 结 1 2 构 （四）凹凸腔 与 坐标系上 g1 1、0 g 2 1 和 g 2 1、0 g1 1 稳 的区域代表第四类腔，即图中的第Ⅳ部分，它是 定 由一块R＜0的凸面镜和一块R＞L的凹面镜构成， 性
（一）对称腔
1 2 第 而坐标原点O则代表R1=R2=L，即共焦腔；A点代表R1=R2→∞，即平行平面腔；B 二 代表R1=R2=L/2，即共心腔。 章 激 （二）长焦距非对称腔 光 在坐标系上 0 g1 1 和 0 g 2 1 的区域，这是第二类腔，即图中的第Ⅱ部分， 器 的 2 代表曲率半径大于腔长的非对称腔。其特点：R1≠R2；R1＞L，R2＞L 工 g2 1 作 （三）短焦距非对称腔 原 光 在坐标系上除去OB的整个 g1 0 和 g 2 0 理 学 的区域，这是第三类腔，即图中的第Ⅲ部分，
§ .
图(2-3) 稳定图的应用
上一页 回首页 下一页 回末页 回目录
2.1.1共轴球面谐振腔的稳定性条件
第 1. 规定曲率半径为R，焦距为f，物距s和象距s´在反射镜前面为正，在反射镜 二 后面的为负，则有： 章 1) 对于凹透镜，R>0，f=R/2>0 激 光 2) 对于凸透镜，R<0，f=R/2<0 器 3) 对于平面镜， R , f 的 2 1 1 1 工 2.成像公式为: 1 作 s s f 原 光 理 学 3.如图(2-1)所示，共轴球面腔的结构可以用三个参数来表示：两个球面反射镜
A O A M2 B
M1
F B 图（2.2.2）(a)半共焦腔
M2
M1
§ .
图（2.2.2）(b)半共心腔
C1
B0Biblioteka h3 A1h01
B'0
F f
h0
A2 O2
O1 h B1 M1
h2
B2 L M2
图（2.2.2）(c)不稳定腔
上一页 回首页 下一页 回末页 回目录
第 二 章 激 光 器 的 2 工 作 1 原 光 理 学
第 2.利用稳定条件可将球面腔分类如下: 二 章 (1) 稳定腔 激 双凹稳定腔，由两个凹面镜组成，对应图中l、2、3和4区 光 器 平凹稳定腔，由一个平面镜和一个凹面镜组成，对应图中AC、AD段 的 2 凹凸稳定腔，由一个凹面镜和一个凸面镜组成，对应图中5区和6区。 工 共焦腔，R1＝R2＝L，因而，g1=0，g2=0，对应图中的坐标原点。 作 1 原 光 半共焦腔，由一个平面镜和一个R=2L的凹面镜组成的腔，对应图中E和F点。 理 学
§ .
结 构 以上三式即为在增益介质中同时存在抽运、吸收、自发辐射和受激辐射时各能级 与 上的粒子数密度随时间变化的速率方程组。 稳 定 性
上一页 回首页 下一页 回末页 回目录
第 二 在反射镜M2上，有：h0 < h2 < h4 < … 章 这种腔中的傍轴光线不能在腔内往返传播任意多次而不逸出腔外。 激 光 5）由上面的分析得出结论：用平、凹反射镜构成的稳定腔其腔长L必须满足 器 L≤2f，否则都是不稳定腔。 的 2 工 作 1 2.1.3 对称凹面镜腔 1. 由两块凹面镜也能组成光学谐振腔，如图（2.2.3）(a)是对称共焦腔，图 原 光 理 学 （2.2.3）(b)是共心腔。
谐 振 腔 结 构 与 稳 定 性
§ .
(2) 临界腔 平行平面腔，对应图中的A点。只有与腔轴平行的光线才能在腔内往返。 共心腔， 满足条件R2＋R2＝L，对应图中第一象限的g1g2＝1的双曲线。 半共焦腔，由一个平面镜和一个凹面镜组成，对应图中C点和D点。 (3) 非稳腔 对应图中阴影部分的光学谐振腔都是非稳腔。