第三章 二维图形基础

4第三章⼆维图形的编辑⽅法（⼀）第三章⼆维图形的编辑⽅法（⼀）课程： AutoCAD2006 应⽤教程授课⽇期： 2006 年⽉⽇第 4 周导⾔：上节课介绍了⼆维图形的绘制⽅法，⽽AutoCAD不仅有强⼤的作图能⼒，还有强⼤的编辑功能，本节课开始介绍⼆维图形的编辑⽅法。

在绘图时，单纯的使⽤绘图命令或绘图⼯具，只能绘制⼀些基本的图形对象。

为了绘制复杂图形，很多情况下都必须借助于图形编辑命令。

1、选择对象直接拾取只需将拾取框移动到希望选择的对象上，并单机⿏标即可。

对象被选择后，会以虚线形式显⽰。

选择全部对象在“选择对象”提⽰下输⼊“ All ”后按“ Enter ”键， AutoCAD 将⾃动选中屏幕上的所有对象默认矩形窗⼝拾取⽅式将拾取框移动到图中空⽩地⽅并单击⿏标，在该提⽰下将光标移到另⼀个位置后单击， AutoCAD ⾃动以这两个拾取点为对⾓点确定⼀个矩形拾取窗⼝。

如果矩形窗⼝是从左向右定义的，那么窗⼝内部的对象均被选中，⽽窗⼝外部以及与窗⼝边界相交的对象不被选中；如果窗⼝是从右向左定义的，那么不仅窗⼝内部的对象被选中，与窗⼝边界相交的那些对象也被选中。

矩形窗⼝拾取⽅式在“选择对象：”提⽰下输⼊“ W ”并按 Enter 键， AutoCAD 会依次提⽰⽤户确定矩形拾取窗⼝内所有对象。

在使⽤矩形窗⼝拾取⽅式时，⽆论是从左向右还是从右向左定义窗⼝，被选中的对象均为位于窗⼝内的对象。

交叉矩形窗⼝拾取⽅式在“选择对象：”提⽰下输⼊“ C ”并按 Enter 键， AutoCAD 会依次提⽰确定矩形拾取窗⼝的两个⾓点，确定矩形拾取窗⼝的两个⾓点后，所选对象不仅包括位于矩形窗⼝内的对象，⽽且也包括与窗⼝边界相交的所有对象。

不规则窗⼝的拾取⽅式在“选择对象：”提⽰下输⼊“ WP ”后按 Enter 键，根据提⽰确定出不规则拾取窗⼝的其他个顶点位置后按 Enter 键， AutoCAD 将选中由这些点确定的不规则窗⼝内的对象。

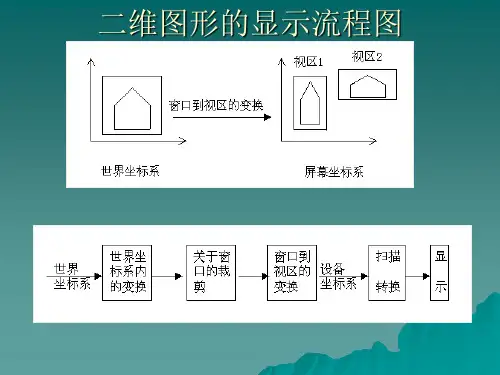
二维形的分类与计算知识点总结二维形指的是平面上的图形，它们是由点、线和曲线组成的。

在数学中，我们可以通过对二维形进行分类来更好地理解和应用数学知识。

同时，对于二维形的计算也有一些特定的知识点需要掌握。

本文将对二维形的分类与计算知识点进行总结，帮助读者更好地掌握这些内容。

一、二维形的分类1. 根据几何特征的分类根据二维形的几何特征，可以将其分为以下几类：（1）点：点是二维形的最基本元素，没有大小和形状。

（2）线段：线段是由两个点连接而成的，具有长度和方向。

（3）直线：直线是没有端点且无限延伸的线段。

（4）射线：射线有一个端点并且无限延伸。

（5）曲线：曲线是由多个点连成的弯曲的线。

（6）多边形：多边形是由多个线段连接而成的封闭图形。

2. 根据边数的分类根据二维形的边数，可以将其分为以下几类：（1）三角形：三角形是由三条线段连接而成的多边形。

（2）四边形：四边形是由四条线段连接而成的多边形。

（3）五边形：五边形是由五条线段连接而成的多边形。

（4）六边形：六边形是由六条线段连接而成的多边形。

3. 根据角度的分类根据二维形的角度，可以将其分为以下几类：（1）锐角三角形：三个内角都是锐角的三角形。

（2）直角三角形：三个内角中有一个是直角的三角形。

（3）钝角三角形：三个内角中有一个是钝角的三角形。

（4）等边三角形：三个内角都是60度的三角形。

4. 根据对称性的分类根据二维形的对称性，可以将其分为以下几类：（1）对称图形：对称图形具有中心对称和轴对称两种形式。

（2）非对称图形：非对称图形没有对称轴或中心。

二、二维形的计算知识点1. 面积计算计算二维形的面积是数学中非常重要的一部分。

不同形状的二维形，其面积计算公式也各不相同。

（1）三角形的面积计算公式为：面积 = 底边长 ×高 / 2。

（2）矩形的面积计算公式为：面积 = 长 ×宽。

（3）圆的面积计算公式为：面积= π × 半径²。

二维几何形知识点总结在数学中，二维几何形是指只具有长和宽两个维度的图形。

在本文中，我们将总结一些常见的二维几何形，并讨论它们的性质和应用。

一、点（Point）点是二维几何中最基本的元素，它不具有长度、宽度和面积。

点通常用大写字母表示，例如点A、点B等。

在二维平面坐标系中，点可以通过坐标表示，例如点A(2, 4)表示坐标为(2, 4)的点A。

二、直线（Line）直线是由无数个点组成，它没有起点和终点，并且在两个方向上无限延伸。

直线可以用两个点确定，也可以用一般方程式来表示。

例如，通过点A(2, 3)和点B(5, 7)可以确定一条直线AB。

三、线段（Line Segment）线段是直线的一部分，具有起点和终点。

线段的长度可以通过两个点之间的距离来计算。

例如，线段AB表示起点为A、终点为B的线段。

四、射线（Ray）射线由一个起点和一个方向确定，从起点出发沿着给定方向无限延伸。

射线可以用其起点和沿着的方向来表示。

例如，从点A(3, 2)出发，沿着向右上方的方向延伸的射线可以表示为从点A开始的射线。

五、角度（Angle）角度是由两条射线的公共起点和旋转方向确定的图形。

角度通常用大写字母表示，例如∠ABC表示由射线AB和射线BC所夹的角度。

角度可以通过度数（°）或弧度（rad）来度量。

六、三角形（Triangle）三角形是由三条线段组成的多边形。

根据边长和角度的不同，三角形可以分为等边三角形、等腰三角形、直角三角形等。

三角形的性质包括三个角的和为180°、任意两边之和大于第三边等。

七、矩形（Rectangle）矩形是由四条边和四个直角组成的四边形。

矩形的性质包括相对边相等、对角线相等且互相平分等。

矩形的面积可以通过长乘以宽来计算。

八、正方形（Square）正方形是一种特殊的矩形，具有相等的边长和四个直角。

正方形的性质包括边长相等、对角线相等、内角为90°等。

正方形的面积可以通过边长的平方来计算。

二维图形的认识与分类在数学中，二维图形是指仅有两个维度（长度和宽度）的平面上的形状或图案。

对二维图形进行正确的认识和分类是学习数学和几何的基础。

本文将详细介绍二维图形的认识与分类，以帮助读者更好地理解和应用。

一、点、线和面1. 点点是二维图形中最基本的元素，它没有长度和宽度，只有位置。

点可以用小写字母标记，如A、B、C等。

2. 线段线段是由两个点确定的直线段，在数学中可以用AB或者直线上的两个点A和B表示。

线段具有长度，但没有宽度。

3. 封闭曲线封闭曲线是由线段首尾相连形成的图形，如圆、椭圆等。

它们具有长度和宽度，并且形状是封闭的。

4. 平行线平行线是在同一个平面上永远不会相交的直线。

它们具有相同的斜率，但是没有交点。

5. 直线直线是没有起点和终点的无限延伸的线段。

直线可以用一对平行线表示，如AB和CD。

6. 折线折线是由多条线段首尾相连形成的图形，每条线段称为折线的一条边。

折线可以是封闭的，也可以是不封闭的。

二、二维图形的分类1. 三角形三角形是由三条线段组成的图形，它们相交于三个顶点，每两条线段的交点称为三角形的顶点。

根据边长和角度的不同，三角形可以分为等边三角形、等腰三角形、直角三角形等。

2. 四边形四边形是由四条线段组成的图形，它们相交于四个顶点。

常见的四边形有矩形、正方形、平行四边形、梯形等。

3. 圆形圆形是一个封闭曲线，它的每个点到圆心的距离都是相等的。

圆形由一个中心和一个半径确定，常用字母O表示圆心，r表示半径。

4. 椭圆椭圆是一个封闭曲线，它的形状呈现类似椭圆形。

椭圆由两个焦点和一个常数和两个焦点的距离之和确定。

5. 多边形多边形是由多条线段组成的图形，它们相交于多个顶点，并且每两条线段的交点不是顶点。

常见的多边形有五边形、六边形、七边形等。

6. 弧线弧线是圆的一部分，它由圆心和起点、终点确定。

弧线可以是封闭的，也可以是不封闭的。

三、二维图形的性质1. 对称性许多二维图形都具有对称性，它们可以通过某条直线、某个点或者某个中心轴进行对称。

二维几何形的基本概念几何学是数学的一个重要分支，研究空间中的形状、大小、位置以及它们之间的关系。

在几何学中，二维几何形是一个基本概念，它们由长度和宽度组成，没有厚度。

二维几何形包括点、线段、直线、角、多边形等。

本文将介绍二维几何形的基本概念，包括其定义、性质和常见的例子。

1. 点：点是二维几何中最基本的概念，它没有大小，只有位置。

点用大写字母表示，比如A、B、C等。

2. 线段：线段是由两个点A和B确定的一段连续的直线。

线段的长度可以用AB表示。

线段的两个端点是A和B，记作$AB$。

3. 直线：直线是由无数个点组成的，这些点沿着同一方向无限延伸。

直线上的任意两点都能确定一条直线。

直线用小写字母表示，比如$l$、$m$。

4. 角：角是由两个线段共享一个公共端点而形成的，称为角的顶点。

角可以用大写字母表示，比如$\angle A$、$\angle B$。

角的大小可以用度数（度）或弧度（弧）来表示。

5. 多边形：多边形是由若干个线段首尾相连而构成的封闭图形。

多边形的边数至少为3条。

常见的多边形有三角形、四边形、五边形等。

多边形的内角之和等于180度。

以上是二维几何形的基本概念，下面我们来看一些常见的二维几何形的例子。

1. 三角形：三角形是由三条线段组成的多边形。

三角形的特点是三条边和三个内角。

根据边的长度，三角形可以分为等边三角形（三边相等）、等腰三角形（两边相等）、直角三角形（一个角为直角）等多种类型。

2. 四边形：四边形是由四条线段组成的多边形。

四边形的特点是四条边和四个内角。

根据边和角的性质，四边形可以分为正方形、长方形、菱形、平行四边形等多种类型。

3. 圆：圆是一个特殊的二维几何形，它由所有与圆心距离相等的点构成。

圆的特点是没有边和角。

圆心到圆上任意点的距离称为半径，圆上任意两点间的距离称为弦。

通过学习和理解二维几何形的基本概念，我们可以更好地解决与形状、大小、位置相关的问题。

在实际应用中，几何学在建筑、工程、地理等领域都有广泛的应用。

二维作图的基础知识点总结一、平面坐标系1. 直角坐标系直角坐标系是二维作图中最常用的坐标系之一，其基本构造原理是由两根相交的直线组成，这两根直线相互垂直，并分别在相交点上各标定一个原点O，然后在两根直线上分别标上数轴，即横轴和纵轴。

通过该坐标系，可以直观表示平面上的点的位置关系。

2. 极坐标系极坐标系是二维作图中另一种常用的坐标系，其特点在于以一个定点和一条射线为基础，在这条射线上选定一个固定方向作为初始方向，然后以这个定点为原点，以这条射线的长度为极轴，和这条射线与初始方向的夹角为极角，来表示平面上的点的位置。

二、基本图形的表示1. 点点是二维作图中的最基本的图形，通常可以用坐标的形式表示，例如( x，y )，其中的x表示该点在横轴上的位置，y表示该点在纵轴上的位置。

2. 直线直线是由无数个点组成的，如果知道直线上两个点的坐标，就可以确定这条直线。

所以在作图中，我们可以通过两个点来表示一条直线。

3. 圆圆是由一个定点（圆心）和一个定长（半径）所构成的。

因此表示一个圆的简便方法是给出这个圆的圆心和半径。

4. 矩形矩形是由4条相互平行且相互垂直的边所构成的，用矩形的两个对角线的交点和矩形的长和宽来表示。

5. 椭圆椭圆是由一个定点（焦点）和两个定长（长轴和短轴）所构成的。

所以表示一个椭圆的简便方法就是给出椭圆的焦点和长短轴。

三、作图的基本方法1. 画直线画直线有多种方法，最基本的是通过给出直线上的两个不同的点，然后用直尺将这两个点连起来，就得到了一条直线。

2. 画圆画圆通常可以通过给定圆心和半径，然后利用圆规在平面上画出一个圆。

3. 画矩形画矩形一般可以通过给出矩形的对角线的交点和矩形的长和宽，然后利用直尺和量角器来画出矩形。

4. 画椭圆画椭圆也可以通过给出椭圆的焦点和长短轴，然后利用圆规和直尺来画出椭圆。

四、作图的基本技巧1. 使用合适的工具在二维作图中，使用合适的工具是非常重要的。

例如在画直线时要使用直尺，画圆时要使用圆规，这样可以大大提高作图的准确性和效率。

二维形的基本概念与性质知识点总结二维形是几何学中一个重要的概念，它指的是一个图形在平面上延伸的形态。

在这篇文章中，我们将对二维形的基本概念与性质进行总结。

在这个过程中，我们将依次介绍点、直线、曲线、多边形和圆等二维形的特点和性质。

点是二维形的基础，它是一个没有大小和形状的几何实体。

点可以用一个大写字母表示，如A、B、C等。

在平面上，通过两个不同的点可以画出一条直线。

直线是由无限多个点组成，它是二维形中最简单的一种形态。

直线可以用两个点表示，也可以用一对坐标表示。

直线有无限延伸的性质，可以无限地延伸至平面的任意位置。

曲线与直线相似，也是由无限多个点组成的。

不同的是，曲线在平面上延伸时会产生弯曲。

曲线通常可以用一定的方程式或描述方法表示，如 y = f(x) 或者极坐标方程等。

多边形是由直线段组成的封闭图形，它有三个或者更多的边和顶点。

三角形、四边形、五边形等都是常见的多边形。

多边形的性质有很多，比如边长、角度、对角线长度等。

例如，三角形的内角和为180度，四边形的对角线互相垂直等。

圆是一个特殊的二维形，它的每个点到圆心的距离都相等。

圆可以用圆心和半径来表示，圆心表示圆的位置，半径表示圆的大小。

圆的性质与多边形有很大的区别，比如圆周长、面积、弧长等。

除了以上介绍的基本概念和性质外，二维形还有一些重要的知识点需要了解。

其中一个是相似形。

相似形是指形状相似但大小不同的二维形。

相似形的对应边的比例相等，对应角的度数也相等，这个性质非常有用，可以用来求解一些几何问题。

另一个重要的知识点是平移、旋转和翻转。

这些是二维形在平面上的变换方式。

平移是指将形状整体移动到平面上的另一个位置，旋转是指将形状按一定角度绕着固定点旋转，翻转是指将形状按照某条直线翻转成镜像形状。

这些变换方式对于解决一些几何问题十分重要。

总之，二维形是几何学中的重要概念，它包括点、直线、曲线、多边形和圆等形态。

每种形态都有其独特的性质和特点。

除此之外，相似形和几何变换也是二维形的重要知识点。

二维形的基本概念与性质二维形是几何学中的重要概念，它是指拥有两个维度（即长度和宽度）的物体或图形。

二维形广泛存在于我们的日常生活中，从平面上的几何图形到电视屏幕上的影像，都是二维形的实例。

本文将探讨二维形的基本概念与性质，以加深对其理解。

一、二维形的基本概念二维形是在平面上存在的物体或图形，它们只有长度和宽度两个维度，没有厚度。

常见的二维形包括平面上的点、线、多边形等。

1. 点：点是二维形中最基础的元素，它不占据任何面积，只有位置信息。

用坐标表示一个点在平面上的位置，如(x, y)。

2. 线：线由无数个点组成，是没有宽度的直线段。

线有长度但没有宽度。

3. 多边形：多边形是由若干条线段组成的封闭图形。

它有边，也有顶点。

常见的多边形有三角形、四边形、五边形等。

二、二维形的性质除了基本概念，二维形还具有一些重要的性质，这些性质对于理解和分析二维形非常有用。

1. 长度和面积二维形的长度可以通过测量线段来确定，而面积可以通过测量图形的表面积来确定。

长度和面积是衡量二维形尺寸的基本指标。

2. 周长和周界多边形具有周长这一重要性质。

周长是指多边形上所有边的长度之和。

周界是指封闭图形的边界长度，对于一些曲线也适用。

3. 角度角度是二维形中重要的概念。

由两条线段交叉形成的夹角可以用来描述二维形的方向和位置关系。

角度的单位通常用弧度或度来表示。

4. 对称性二维形可以具有对称性。

对称形是指具有对称轴（或中心）的图形，它们在对称轴两侧呈现镜像关系。

对称性是二维形中常见的性质，可以用来简化问题和构造美观的图形。

5. 相似性相似性是二维形的一种重要性质。

如果两个二维形的形状相似，它们的对应边长成比例，对应角度相等。

相似性在几何学和工程中具有广泛的应用。

结论二维形是几何学中的重要概念，它涉及到平面上的点、线和多边形等形状。

二维形具有一些基本的性质，如长度、面积、周长和角度等。

这些性质对于理解和分析二维形非常有用，并在实际应用中发挥着重要的作用。

二维形的认知与分类知识点总结在学习过程中，我们会遇到各种各样的知识点。

本文将对二维形的认知与分类进行总结。

二维形是平面上的图形，包括了点、线、圆和各种多边形。

了解二维形的特性和分类对于数学学习至关重要。

1. 点、线和圆- 点是最基本的二维形，没有长度、面积和体积。

它只有位置，用坐标表示。

- 线是由多个点连接而成的，可以是直线或曲线。

线的特点是无宽度，只有长度。

- 圆是由一个固定点到平面上任意一点的距离都相等的轨迹形成的。

圆由圆心和半径来确定。

2. 多边形- 多边形是由直线段相连而成的封闭图形，边数大于等于3。

根据边的长度和角的大小，多边形可以进行分类。

- 三角形是最简单的多边形，有三条边和三个内角。

根据边的长度和角的大小，可以分为等边三角形、等腰三角形和一般三角形。

- 四边形是有四条边和四个内角的多边形。

根据边的长度和角的大小，可以分为正方形、长方形、菱形和一般四边形。

- 多边形还可以根据边的形状进行分类。

例如，凸多边形的内角都小于180度，而凹多边形有至少一个内角大于180度。

3. 相似与全等- 两个二维形如果形状相同但大小不同，我们称它们为相似形。

相似形的对应边长成比例，对应角相等。

- 两个二维形如果形状和大小都相同，我们称它们为全等形。

全等形的对应边和对应角都相等。

4. 计算二维形的面积和周长- 计算面积和周长是学习二维形的重要部分。

根据不同的二维形，有不同的计算公式。

- 点没有面积和周长。

- 线没有面积，只有长度。

- 圆的面积公式是πr²，周长公式是2πr。

- 三角形的面积公式是底乘以高的一半，周长是三边之和。

- 长方形的面积公式是长乘以宽，周长是两倍长加两倍宽。

- 正方形的面积公式是边长的平方，周长是边长的四倍。

5. 实际应用- 二维形的认知和分类不仅仅是学习的目的，还与实际生活息息相关。

- 在建筑设计中，了解不同形状和大小的二维形有助于设计出更美观和实用的建筑物。

- 在地图导航中，通过二维形的认知和分类，我们能够更准确地查找地点和规划路线。