公差分析简介及实例分析共15页

统计公差分析方法概述(2012-10-23 19:45:32)分类：公差设计统计六标准差统计公差分析方法概述一.引言公差设计问题可以分为两类：一类是公差分析(Tolerance Analysis ,又称正计算) ,即已知组成环的尺寸和公差,确定装配后需要保证的封闭环公差；另一类是公差分配(Tolerance Allocation ,又称反计算) ,即已知装配尺寸和公差,求解组成环的经济合理公差。

公差分析的方法有极值法和统计公差方法两类,根据分布特性进行封闭环和组成环公差的分析方法称为统计公差法.本文主要探讨统计公差法在单轴向(One Dimension)尺寸堆叠中的应用。

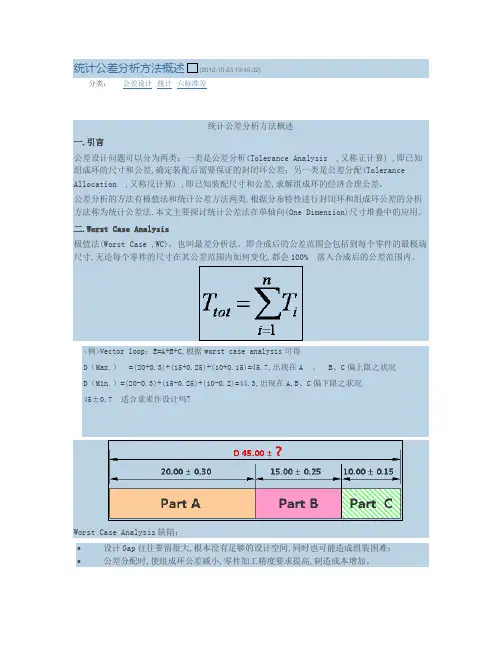
二.Worst Case Analysis极值法(Worst Case ,WC)，也叫最差分析法，即合成后的公差范围会包括到每个零件的最极端尺寸,无论每个零件的尺寸在其公差范围内如何变化,都会100% 落入合成后的公差范围内。

<例>Vector loop：E=A+B+C,根据worst case analysis可得D（Max.）=(20+0.3)+(15+0.25)+(10+0.15)=45.7,出现在A、B、C偏上限之状况D（Min.）=(20-0.3)+(15-0.25)+(10-0.2)=44.3,出现在A,B、C偏下限之状况45±0.7适合拿来作设计吗?Worst Case Analysis缺陷：•设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难；•公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。

以上例Part A +Part B+ Part C，假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平，则每个部材的不良机率为1-0.9973=0.0027；在组装完毕后所有零件都有缺陷的机率为：0.0027^3=0.000000019683。

这表明几个或者多个零件在装配时,同一部件的各组成环,恰好都是接近极限尺寸的情况非常罕见。

公差分析报告基本知识公差分析是工程设计中非常重要的一项技术，它主要用于确定产品制造过程中所允许的尺寸变差范围，以保证产品在使用过程中的正常功能。

本篇文章将介绍公差分析的基本知识，包括公差的定义、公差的类型、公差的表示方法、公差链和公差分析方法等内容。

一、公差的定义公差是指将产品实际尺寸与设计尺寸之间的差值，它是制约产品功能和性能的重要因素。

公差是在设计阶段就需要考虑和确定的，通过公差的控制可以保证产品在制造和使用过程中的稳定性和可靠性。

二、公差的类型1.一般公差：是指对于产品的一般尺寸，根据所处的尺寸量级和表面质量要求而规定的公差。

2.几何公差：是指控制产品几何形状和位置关系的公差，包括平面度、圆度、圆柱度、直线度、平行度、垂直度等。

3.形位公差：是指产品形状和位置关系的公差，包括位置公差、姿态公差、形位公差、轴向公差等。

4.配合公差：是指对于产品的配合尺寸，根据配合要求而规定的公差，包括间隙、过盈和配合紧度等。

三、公差的表示方法公差的表示方法主要有四种：1.加减公差法：即在设计尺寸基础上，通过加减法确定上下限公差。

2.限界公差法：即在设计尺寸基础上，通过上限和下限值确定公差范围。

3.基础尺寸法：即以一个基础尺寸作为基准，通过加减公差法确定其他尺寸的上下限公差。

4. 数值公差法：即通过数值来表示公差的大小，如0.01mm、0.1mm 等。

四、公差链公差链是指产品由多个零件组成时，各个零件公差相加所形成的总公差。

在进行公差分析时，需要考虑到各种公差之间的相互关系和叠加效应，以保证整体装配的精度和可靠性。

五、公差分析方法公差分析有多种方法，主要包括：1.构造法：根据零件的功能要求，通过构造关系和尺寸链的分析，确定零件的公差。

2.统计法：通过对产品和工艺数据的统计分析，确定公差的适用范围和控制要求。

3.模拟法：通过建立数学模型，模拟产品在设计和制造过程中的变化和误差，分析公差对产品性能的影响。

4.比较法：通过对已有样品或标准件的测量和分析，确定公差的适用范围和控制要求。

公差分析一、误差与公差二、尺寸链三、形位公差及公差原则一、误差与公差（一）误差与公差的基本概念1. 误差误差——指零件加工后的实际几何参数相对于理想几何参数之差。

（1）零件的几何参数误差分为尺寸误差、形状误差、位置误差及表面粗糙度。

尺寸误差——指零件加工后的实际尺寸相对于理想尺寸之差，如直径误差、孔径误差、长度误差。

形状误差（宏观几何形状误差）——指零件加工后的实际表面形状相对于理想形状的差值，如孔、轴横截面的理想形状是正圆形，加工后实际形状为椭圆形等。

相对位置误差——指零件加工后的表面、轴线或对称面之间的实际相互位置相对于理想位置的差值，如两个面之间的垂直度，阶梯轴的同轴度等。

表面粗糙度（微观几何形状误差）——指零件加工后的表面上留下的较小间距和微笑谷峰所形成的不平度。

2. 公差公差——指零件在设计时规定尺寸变动范围，在加工时只要控制零件的误差在公差范围内，就能保证零件的互换性。

因此，建立各种几何公差标准是实现对零件误差的控制和保证互换性的基础。

（二）误差与公差的关系由图1（三）公差术语及示例图2以图2为例：基本尺寸——零件设计中，根据性能和工艺要求，通过必要的计算和实验确定的尺寸，又称名义尺寸，图中销轴的直径基本尺寸为Φ20，长度基本尺寸为40。

实际尺寸——实际测量的尺寸。

极限尺寸——允许零件实际尺寸变化的两个极限值。

两个极限值中大的是最大极限尺寸，小的是最小极限尺寸。

尺寸偏差——某一尺寸（实际尺寸，极限尺寸）减去基本尺寸所得到的代数差。

上偏差=最大极限尺寸-基本尺寸，用代号（ES）（孔）和es（轴）下偏差=最小极限尺寸-基本尺寸，用代号（ES）（孔）和es（轴）尺寸公差——允许尺寸的变动量尺寸公差=最大极限尺寸-最小极限尺寸公差带零线——在极限与配合图解中，标准基本尺寸是一条直线，以其为基准确定偏差和公差。

通常，零件沿水平方向绘制，正偏差位于其上，负偏差位于其下，如下图。

图3公差带图解公差带——在公差带图解中，由代表上极限偏差和下极限偏差的两条直线所限定的一个区域。

公差分析基本知识公差分析一、误差与公差二、尺寸链三、形位公差及公差原则一、误差与公差（一）误差与公差的基本概念1. 误差误差——指零件加工后的实际几何参数相对于理想几何参数之差。

（1）零件的几何参数误差分为尺寸误差、形状误差、位置误差及表面粗糙度。

尺寸误差——指零件加工后的实际尺寸相对于理想尺寸之差，如直径误差、孔径误差、长度误差。

形状误差（宏观几何形状误差）——指零件加工后的实际表面形状相对于理想形状的差值，如孔、轴横截面的理想形状是正圆形，加工后实际形状为椭圆形等。

相对位置误差——指零件加工后的表面、轴线或对称面之间的实际相互位置相对于理想位置的差值，如两个面之间的垂直度，阶梯轴的同轴度等。

表面粗糙度（微观几何形状误差）——指零件加工后的表面上留下的较小间距和微笑谷峰所形成的不平度。

2. 公差公差——指零件在设计时规定尺寸变动围，在加工时只要控制零件的误差在公差围，就能保证零件的互换性。

因此，建立各种几何公差标准是实现对零件误差的控制和保证互换性的基础。

（二）误差与公差的关系由图1可知，零件误差是公差的子集，误差是相对于单个零件而言的；公差是设计人员规定的零件误差的变动围。

（三）公差术语及示例图2以图2为例：基本尺寸——零件设计中，根据性能和工艺要求，通过必要的计算和实验确定的尺寸，又称名义尺寸，图中销轴的直径基本尺寸为Φ20，长度基本尺寸为40。

实际尺寸——实际测量的尺寸。

极限尺寸——允许零件实际尺寸变化的两个极限值。

两个极限值的是最大极限尺寸，小的是最小极限尺寸。

公差零件误差零件误差图1尺寸偏差——某一尺寸（实际尺寸，极限尺寸）减去基本尺寸所得到的代数差。

上偏差=最大极限尺寸-基本尺寸，用代号（ES）（孔）和es（轴）下偏差=最小极限尺寸-基本尺寸，用代号（ES）（孔）和es（轴）尺寸公差——允许尺寸的变动量尺寸公差=最大极限尺寸-最小极限尺寸公差带零线——在极限与配合图解中，标准基本尺寸是一条直线，以其为基准确定偏差和公差。

欢迎阅读公差分析一、误差与公差二、尺寸链三、形位公差及公差原则际相互位置相对于理想位置的差值，如两个面之间的垂直度，阶梯轴的同轴度等。

表面粗糙度（微观几何形状误差）——指零件加工后的表面上留下的较小间距和微笑谷峰所形成的不平度。

2. 公差公差——指零件在设计时规定尺寸变动范围，在加工时只要控制零件的误差在公差范围内，就能保证零件的互换性。

因此，建立各种几何公差标准是实现对零件误差的控制和保证互换性的基础。

（二）误差与公差的关系由图1可知，零件误差是公差的子集，误差是相对于单个零件而言的；公差是设计人员规定的零件误差的变动范围。

（三）公差术语及示例图2以图2为例：基本尺寸——零件设计中，根据性能和工艺要求，通过必要的计算和实验确定的尺寸，又称名义尺寸，图中销轴的直径基本尺寸为Φ20，长度基本尺寸为40。

实际尺寸——实际测量的尺寸。

极限尺寸——允许零件实际尺寸变化的两个极限值。

两个极限值中大的是最大极限尺寸，小的是最小极限尺寸。

尺寸偏差——某一尺寸（实际尺寸，极限尺寸）减去基本尺寸所得到的代数差。

上偏差=最大极限尺寸-基本尺寸，用代号（ES ）（孔）和es （轴） 下偏差=最小极限尺寸-基本尺寸，用代号（ES ）（孔）和es （轴） 公差 图1尺寸公差——允许尺寸的变动量尺寸公差=最大极限尺寸-最小极限尺寸公差带零线——在极限与配合图解中，标准基本尺寸是一条直线，以其为基准确定偏差和公差。

通常，零件沿水平方向绘制，正偏差位于其组成环又分为增环和减环增环——当某一组成环增加（减小），其他组成环都不变时，封闭环也增加（减小）。

减环——当某一组成环减小（增加），其他组成环都不变时，封闭环增加（减小）。

尺寸链建立1、确定要计算的目标值（闭环）。

2、找到与目标值相关的所有零件尺寸。

3、根据装配关系，建立尺寸链，目标尺寸是相关零件安照一定的装配顺序得到的。

设尺寸链中组成环的个数为m，其中有n个增环，A1为组成环的基本尺寸，对于直线尺寸链计算公式如下：1）封闭环的基本尺寸封闭环的基本尺寸是尺寸链中所有增环的基本尺寸之和减去尺寸链中所有减环的基本尺寸A 0=∑A i m i=1−∑A j n−1j=m+12）最大最小极限尺寸封闭环的最大极限尺寸是尺寸链中所有增环的最大极限尺寸之和减去所有减环的最小极限尺寸之和，同理得封闭环最小极限尺寸在零件加工过程中，当各环的实际误差不等于各环的公差时，封闭环的实际误差等于所有组成环的误差之和C 0=∑?C i n−1i=16）封闭环的中间尺寸与中间偏差封闭环的中间尺寸是最大值与最小值之和的平均值C 0av =C 0max +C 0min 2封闭环的中间尺寸等于所有增环的中间尺寸之和减去所有减环中间尺寸之和C 0av =∑C iav m i=1-∑Cjav n−1j=m+1 中间偏差是上下偏差的平均值，也是公差带的中心坐标，封闭环的X-Y~(μ1- μ2, σ12- σ22)在大批量的生产中，一个尺寸链中的个组成环尺寸的获得彼此没有关系，因此，可将他们看成是相互独立的随机变量，经大量实测数据后，从概率的概念来看，有两个特征数：算术平均数:这个数值表示尺寸的分布集中的位置均方根偏差σ：说明实际尺寸分布相对于算术平均值的离散程度将极限尺寸换算成平均尺寸C av=C max+C min2σ0=∑σii=1传递系数：各组成环对封闭环影响大小的系数假设尺寸链各环尺寸的分布范围与尺寸公差相一致尺寸链中各组成环的平均尺寸等于各组成环的尺寸的平均值各尺环的尺寸公差都等于各环尺寸标准差的6倍，即6σ组成环尺寸分布偏离正态分布时，用下面公式进行近似：n−1T ok=k√∑T i2i=1。

欢迎阅读公差分析一、误差与公差二、尺寸链三、形位公差及公差原则际相互位置相对于理想位置的差值，如两个面之间的垂直度，阶梯轴的同轴度等。

表面粗糙度（微观几何形状误差）——指零件加工后的表面上留下的较小间距和微笑谷峰所形成的不平度。

2. 公差公差——指零件在设计时规定尺寸变动范围，在加工时只要控制零件的误差在公差范围内，就能保证零件的互换性。

因此，建立各种几何公差标准是实现对零件误差的控制和保证互换性的基础。

（二）误差与公差的关系由图1可知，零件误差是公差的子集，误差是相对于单个零件而言的；公差是设计人员规定的零件误差的变动范围。

（三）公差术语及示例图2以图2为例：基本尺寸——零件设计中，根据性能和工艺要求，通过必要的计算和实验确定的尺寸，又称名义尺寸，图中销轴的直径基本尺寸为Φ20，长度基本尺寸为40。

实际尺寸——实际测量的尺寸。

极限尺寸——允许零件实际尺寸变化的两个极限值。

两个极限值中大的是最大极限尺寸，小的是最小极限尺寸。

尺寸偏差——某一尺寸（实际尺寸，极限尺寸）减去基本尺寸所得到的代数差。

上偏差=最大极限尺寸-基本尺寸，用代号（ES ）（孔）和es （轴） 下偏差=最小极限尺寸-基本尺寸，用代号（ES ）（孔）和es （轴） 公差 图1尺寸公差——允许尺寸的变动量尺寸公差=最大极限尺寸-最小极限尺寸公差带零线——在极限与配合图解中，标准基本尺寸是一条直线，以其为基准确定偏差和公差。

通常，零件沿水平方向绘制，正偏差位于其组成环又分为增环和减环增环——当某一组成环增加（减小），其他组成环都不变时，封闭环也增加（减小）。

减环——当某一组成环减小（增加），其他组成环都不变时，封闭环增加（减小）。

尺寸链建立1、确定要计算的目标值（闭环）。

2、找到与目标值相关的所有零件尺寸。

3、根据装配关系，建立尺寸链，目标尺寸是相关零件安照一定的装配顺序得到的。

设尺寸链中组成环的个数为m，其中有n个增环，A1为组成环的基本尺寸，对于直线尺寸链计算公式如下：1）封闭环的基本尺寸封闭环的基本尺寸是尺寸链中所有增环的基本尺寸之和减去尺寸链中所有减环的基本尺寸A 0=∑A i m i=1−∑A j n−1j=m+12）最大最小极限尺寸封闭环的最大极限尺寸是尺寸链中所有增环的最大极限尺寸之和减去所有减环的最小极限尺寸之和，同理得封闭环最小极限尺寸在零件加工过程中，当各环的实际误差不等于各环的公差时，封闭环的实际误差等于所有组成环的误差之和C 0=∑?C i n−1i=16）封闭环的中间尺寸与中间偏差封闭环的中间尺寸是最大值与最小值之和的平均值C 0av =C 0max +C 0min 2封闭环的中间尺寸等于所有增环的中间尺寸之和减去所有减环中间尺寸之和C 0av =∑C iav m i=1-∑Cjav n−1j=m+1 中间偏差是上下偏差的平均值，也是公差带的中心坐标，封闭环的X-Y~(μ1- μ2, σ12- σ22)在大批量的生产中，一个尺寸链中的个组成环尺寸的获得彼此没有关系，因此，可将他们看成是相互独立的随机变量，经大量实测数据后，从概率的概念来看，有两个特征数：算术平均数:这个数值表示尺寸的分布集中的位置均方根偏差σ：说明实际尺寸分布相对于算术平均值的离散程度将极限尺寸换算成平均尺寸C av=C max+C min2σ0=∑σii=1传递系数：各组成环对封闭环影响大小的系数假设尺寸链各环尺寸的分布范围与尺寸公差相一致尺寸链中各组成环的平均尺寸等于各组成环的尺寸的平均值各尺环的尺寸公差都等于各环尺寸标准差的6倍，即6σ组成环尺寸分布偏离正态分布时，用下面公式进行近似：n−1T ok=k√∑T i2i=1。

欢迎阅读公差分析一、误差与公差二、尺寸链三、形位公差及公差原则际相互位置相对于理想位置的差值，如两个面之间的垂直度，阶梯轴的同轴度等。

表面粗糙度（微观几何形状误差）——指零件加工后的表面上留下的较小间距和微笑谷峰所形成的不平度。

2. 公差公差——指零件在设计时规定尺寸变动范围，在加工时只要控制零件的误差在公差范围内，就能保证零件的互换性。

因此，建立各种几何公差标准是实现对零件误差的控制和保证互换性的基础。

（二）误差与公差的关系由图1可知，零件误差是公差的子集，误差是相对于单个零件而言的；公差是设计人员规定的零件误差的变动范围。

（三）公差术语及示例图2以图2为例：基本尺寸——零件设计中，根据性能和工艺要求，通过必要的计算和实验确定的尺寸，又称名义尺寸，图中销轴的直径基本尺寸为Φ20，长度基本尺寸为40。

实际尺寸——实际测量的尺寸。

极限尺寸——允许零件实际尺寸变化的两个极限值。

两个极限值中大的是最大极限尺寸，小的是最小极限尺寸。

尺寸偏差——某一尺寸（实际尺寸，极限尺寸）减去基本尺寸所得到的代数差。

上偏差=最大极限尺寸-基本尺寸，用代号（ES ）（孔）和es （轴） 下偏差=最小极限尺寸-基本尺寸，用代号（ES ）（孔）和es （轴） 公差 图1尺寸公差——允许尺寸的变动量尺寸公差=最大极限尺寸-最小极限尺寸公差带零线——在极限与配合图解中，标准基本尺寸是一条直线，以其为基准确定偏差和公差。

通常，零件沿水平方向绘制，正偏差位于其组成环又分为增环和减环增环——当某一组成环增加（减小），其他组成环都不变时，封闭环也增加（减小）。

减环——当某一组成环减小（增加），其他组成环都不变时，封闭环增加（减小）。

尺寸链建立1、确定要计算的目标值（闭环）。

2、找到与目标值相关的所有零件尺寸。

3、根据装配关系，建立尺寸链，目标尺寸是相关零件安照一定的装配顺序得到的。

设尺寸链中组成环的个数为m，其中有n个增环，A1为组成环的基本尺寸，对于直线尺寸链计算公式如下：1）封闭环的基本尺寸封闭环的基本尺寸是尺寸链中所有增环的基本尺寸之和减去尺寸链中所有减环的基本尺寸A 0=∑A i m i=1−∑A j n−1j=m+12）最大最小极限尺寸封闭环的最大极限尺寸是尺寸链中所有增环的最大极限尺寸之和减去所有减环的最小极限尺寸之和，同理得封闭环最小极限尺寸在零件加工过程中，当各环的实际误差不等于各环的公差时，封闭环的实际误差等于所有组成环的误差之和C 0=∑?C i n−1i=16）封闭环的中间尺寸与中间偏差封闭环的中间尺寸是最大值与最小值之和的平均值C 0av =C 0max +C 0min 2封闭环的中间尺寸等于所有增环的中间尺寸之和减去所有减环中间尺寸之和C 0av =∑C iav m i=1-∑Cjav n−1j=m+1 中间偏差是上下偏差的平均值，也是公差带的中心坐标，封闭环的X-Y~(μ1- μ2, σ12- σ22)在大批量的生产中，一个尺寸链中的个组成环尺寸的获得彼此没有关系，因此，可将他们看成是相互独立的随机变量，经大量实测数据后，从概率的概念来看，有两个特征数：算术平均数:这个数值表示尺寸的分布集中的位置均方根偏差σ：说明实际尺寸分布相对于算术平均值的离散程度将极限尺寸换算成平均尺寸C av=C max+C min2σ0=∑σii=1传递系数：各组成环对封闭环影响大小的系数假设尺寸链各环尺寸的分布范围与尺寸公差相一致尺寸链中各组成环的平均尺寸等于各组成环的尺寸的平均值各尺环的尺寸公差都等于各环尺寸标准差的6倍，即6σ组成环尺寸分布偏离正态分布时，用下面公式进行近似：n−1T ok=k√∑T i2i=1。