圆周角2

圆周角定理的推论2及圆
圆周角定理是几何学中的重要定理，它指的是：在任意三角形中，其三个内角的和为180°；而在任意园形内，相应的三角形所有内角的和为园周角，即360°，这就是圆周角定理。

圆周角定理是根据三角形和圆形的基础知识来说明的，其中三角形在几何学中是一种重要的几何体，其有三个角度。

任意三角形中，其三个角度的和是180°，而圆则是一个完整的圆形，因而其一个圈中包含了好多条边缘，所有的角度的和就是360°，这也正好等于园周角。

圆周角定理的推论2是：如果三点不在一条直线上，则这三点可以构成一个三角形，而在三角形内，其三个内角的和为180°；另一方面，一个圆中包含了很多条边缘，而它们如果组成三角形，那么它们的和是360°，因此，三角形内角的和等于园周角的和，就是圆周角定理。

因此，圆周角定理的推论2的意义在于，它使得对于所有的园形，可以很容易构绘出来，也可以更方便地计算出其内部的角度数。

圆周角定理的推论2也可以用来帮助解决许多几何问题，比如求椭圆的长短轴长度等。

总而言之，圆周角定理是一个重要的定理，它反映了三角形和圆形之间的关系，并由此推论出了圆周角定理的推论2，使得求解复杂几何问题更加容易，不仅提高了几何的计算应用，而且也成为了几何学的一大宝贵知识。

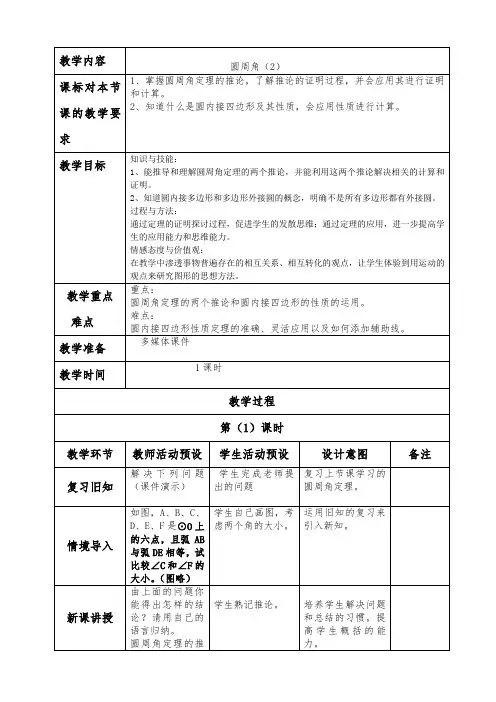
圆周角〔第二课时〕〔张丹丹〕一、教学目标〔一〕学习目标1探索同圆或等圆中，相等的圆周角所对的弧和弦的关系2探索同弦所对圆周角的关系3记住圆周角定理的推论并能运用其解决实际问题4知道圆内接多边形及多边形的外接圆的概念，掌握圆的内接四边形的性质〔二〕学习重点1探索同圆或等圆中，相等的圆周角所对的弧的关系2知道圆内接多边形及多边形的外接圆的概念，掌握圆的内接四边形的性质〔三〕学习难点1探索同弦所对圆周角的关系2圆的内接四边形中对角的关系二、教学设计〔一〕课前设计1预习任务〔1〕在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧和弦也相等．〔2〕在同圆或等圆中，同弦所对的圆周角相等或互补．〔3〕圆内接四边形的对角互补．2预习自测〔1〕如图，A，B，C是⊙O上三点，∠ACB=25°，那么∠BAO的度数是〔〕A．55°B．60°C．65°D．70°【知识点】圆周角定理．【数学思想】数形结合【解题过程】解：连接OB，∵∠ACB=25°，∴∠AOB=2×25°=50°，由OA=OB，∴∠BAO=∠ABO，∴∠BAO=〔180°﹣50°〕=65°．应选C．【思路点拨】连接OB，要求∠BAO的度数，只要在等腰三角形OAB中求得一个角的度数即可得到答案，利用同弧所对的圆周角是圆心角的一半可得∠AOB=50°，然后根据等腰三角形两底角相等和三角形内角和定理即可求得．【答案】C．〔2〕如图，AB是⊙O的直径，BC是⊙O的弦．假设∠OBC=60°，那么∠BAC的度数是〔〕A．75°B．60°C．45°D．30°【知识点】圆周角定理．【数学思想】数形结合【解题过程】解：∵AB是⊙O的直径，∴∠ACB=90°，又∵∠OBC=60°，∴∠BAC=180°﹣∠ACB﹣∠ABC=30°．应选D．【思路点拨】根据AB是⊙O的直径可得出∠ACB=90°，再根据三角形内角和为180°以及∠OBC=60°，即可求出∠BAC的度数．【答案】D．〔3〕如图，点A、B、C、D在⊙O上，O点在∠D的内部，四边形OABC为平行四边形，那么∠OAD∠OCD=度．【知识点】圆周角定理；平行四边形的性质【数学思想】数形结合【解题过程】解：连接OB∵四边形OABC为平行四边形∴AB=OC=OB=OA=BC∴△OAB和△OBC都为等边三角形∴∠OAB=∠OCB=60°∵四边形ABCD为圆的内接四边形∴∠DAB∠DCB=180°∴∠OAD∠OCD=180°﹣60°﹣60°=60°【思路点拨】由四边形OABC为平行四边形，根据平行四边形对角相等，即可得∠B=∠AOC，由圆周角定理，可得∠AOC=2∠ADC，又由内接四边形的性质，可得∠B∠ADC=180°，即可求得∠B=∠AOC=12021∠ADC=60°，然后由三角形外角的性质，即可求得∠OAD∠OCD的度数．【答案】60°〔4〕如图，AB为⊙O的直径，AB=AC，AC交于⊙O点E，∠BAC=45°．假设AE=1，那么BC=．【知识点】圆周角定理；等腰直角三角形【数学思想】数形结合【解题过程】解：∵AB是圆的直径，∴∠AEB=90°，又∵∠BAC=45°，∴△ABE是等腰直角三角形，那么AB=，BE=AE=1，那么EC=AC﹣AE=AB﹣AE=﹣1，在直角△BCE中，BC=．故答案是：．【思路点拨】首先利用圆周角定理证明△ABE是等腰直角三角形，那么求得AB、BE的长度，那么EC即可求得，然后再在直角△BCE中，利用勾股定理即可求解．【答案】二课堂设计1知识回忆〔1〕把顶点在圆上，并且两边都与圆相交的角叫做圆周角。

5.3 圆周角（2）
鞍湖实验学校九年级数学备课组
学习目标
1、熟练应用圆周角定理及其推论解决有关的计算和证明的问题
2、在综运应用圆周角的有关性质解决一些运用问题过程中，进一步培养观察、分析和解决问题的能力
学习重、难点
重点：圆周角定理及其推论的应用；难点：熟练应用圆周角定理及其推论
学习过程：
一、情境创设
我们学习过哪些与圆有关的角？它们之间有什么关系？
二、探索活动
1、如图，BC 为⊙O 的直径，它所对的圆周角是锐角、钝角，还是直角？
2、如图，圆周角∠BAC=90°，弦BC 经过圆心吗？为什么？（以上两个问题，小组交流，让学生自主探索解决）
通过上面的探索发现了什么？
结论：直径（或半圆）所对的圆周角是直角。

90°的圆周角所对的弦是直径。

三、例题解析
例 1 如图，AB 是⊙O 的直径，弦CD 与AB ∠ACD=60°, ∠ADC=50°，求∠CEB 的度数。

B
B C B C
（1） （2）
例 2 已知：如图，△ABC的3个顶点都在⊙
AD是△ABC的高，AE是⊙O的直径，△ABE与△ACD
B 为什么？
本题的变形将△ABE与△ACD相似吗？变成线段AB、AC
在这样的关系？为什么？
四、课堂练习
1、P121练习1、
2、3
2、课课练P97、1-3
五、课堂小结
1、本节课你有什么收获？
2、你还有哪些疑问？
六、作业
课堂作业：P122 习题5.3 7、8、9
家庭作业：完成课课练P97-98;预习书P124-126.。

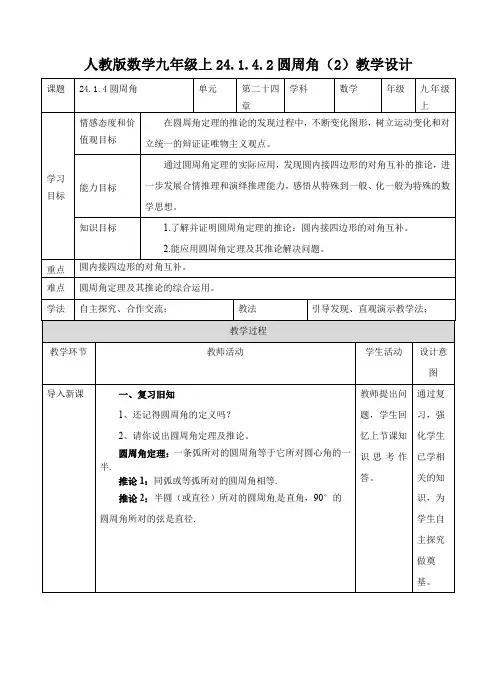
人教版数学九年级上24.1.4.2圆周角（2）教学设计一、复习旧知1、还记得圆周角的定义吗？2、请你说出圆周角定理及推论。

圆周角定理：一条弧所对的圆周角等于它所对圆心角的一半.推论1：同弧或等弧所对的圆周角相等.推论2：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.二、探究新知活动1，抢答：1.你能用三角尺画出下面这个圆的圆心吗？2.填空：如图，∠BAC=55°，∠CAD=45°，则∠DBC=_____°，∠BDC=_____°，∠BCD=______°3.如图，BD是⊙O的直径，∠ABC=130°则∠ADC=______°活动2：讨论请看我们做的抢答习题第2、3题，同学们有没有发现什么规律，请大家以小组为单位讨论后发言。

学生小组1回答：这个四边形的四个顶点，点A，点B，点C，点D都在⊙O上。

学生小组2回答：这个四边形的对角和是180°。

学生小组3回答：……学生小组4回答：……教师总结：同学们真是火眼金睛，找到的特点很多。

这个四边形有一个特点，四边形的四个顶点，点A，点B，点C，点D都在⊙O上，我们把这个四边形叫做圆内接四边形（板书：⊙O叫做四边形ABCD的外接圆）师：出示圆内接三角形图片，并指出：这是一个三角形，这个三角形的所有顶点都在这个圆上，我们把这个三角形叫做圆内接三角形，把这个圆叫做这个三角形的外接圆.师：出示圆内接五边形图片，并指出：这是五边形，这个五边形的所有顶点都在这个圆上，我们把这个五边形叫做圆内接五边形，把这个圆叫做这个五边形的外接圆.师：（出示圆内接六边形图片）归纳总结：现在，同学们能总结出“圆内接多边形”的定义了吗？一般地说，如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.刚才有同学说习题中的四边形的对角和是180°，我们再来看圆内接四边形有什么性质。

24.1．4 圆周角（2）活动五推荐作业，延展新知分类推荐、分层要求，将探究兴趣由课内延伸到课外；及时捕捉学生学习状况，适时进行有效诊断评价、反馈补救、长善救失。

教学程序问题与情境师生互动媒体使用与教学评价活动一创设情境，导入新课一、旧知回放:1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征：①角的顶点在圆上.②角的两边都与圆相交.2、圆心角与所对的弧的关系3、圆周角与所对的弧的关系4、同弧所对的圆心角与圆周角的关系【教师活动】（1）出示问题并引导学生思考回顾（2）关注并适时评价学生的表现。

（3）对学生的表现补充纠正。

【学生活动】（1）思考回顾旧知。

（2）关注教师的评价【媒体使用】出示问题及各种解答结果。

【赏析】复习已学的知识为本节课探索圆周角定理的推论铺平道路。

活动二诱导尝试，探究新知问题1：半圆（或直径）所对的圆周角是多少度？半圆（或直径）所对的圆周角是直角（用于判断某个圆周角是否是直角）问题2：90°的圆周角所对的弦是什么?【教师活动】（1）根据学生活动进程依次出示问题1、2以及思考。

（2）组织学生分组讨论、合作学习，完成问题1、2。

（3）提问两三名学生代表发言，并说出探究过程与理由，老师点【媒体使用】依次出示问题1、2及思考，结合学生活动展示圆周角的推论。

【赏析】（1）加深对圆周角定义的理解。

（2）让学生亲自观察、实验、探究、90°的圆周角所对的弦是圆的直径（用于判断某条线是否过圆心）思考：如图:四边形ABCD中, ∠A 与∠C, ∠B与∠D有何关系?如果一个多边形的所有定点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆角做这个多边形的外接圆。

圆内接四边形的性质：圆内接四边形的对角互补。

评。

对于问题1，教师应重点关注学生是否能由半圆（或直径）所对的圆心角的度数得出圆周角的度数；问题2，教师应重点关注学生是否由90°的圆周角推出同弧所对的圆心角的度数是180°，从而得出所对的弦是直径。

圆周角一、新课导入1.导入课题：情景：如图，把圆心角∠AOB的顶点O拉到圆上，得到∠ACB.问题1：∠ACB有什么特点？它与∠AOB有何异同？问题2：你能仿照圆心角的定义给∠ACB取一个名字并下个定义吗？由此导入课题.〔板书课题〕2.学习目标：(1)知道什么是圆周角，并能从图形中准确识别它.(2)探究并掌握圆周角定理及其推论.(3)体会“由特殊到一般〞“分类〞“化归〞等数学思想.3.学习重、难点：重点：圆周角定理及其推论.难点：圆周角定理的证明与运用.二、分层学习1.自学指导：〔1〕自学内容：教材第85页到第86页倒数第6行之前的内容. 〔2〕自学时间：10分钟.〔3〕自学方法：完成探究提纲.〔4〕探究提纲：1〕圆周角的概念①顶点在圆上，并且两边都与圆相交的角叫做圆周角.②判别以下各图中的角是不是圆周角，并说明理由.②猜一猜：一条弧所对的圆周角与圆心角有何数量关系？②量一量：用量角器量一量圆心角∠AOB和圆周角∠ACB.a.如图，∠ACB=12∠AOB.b.你可以画多少个AB所对的圆周角？这些圆周角与∠AOB之间有什么数量关系？∠AOB的一半.③想一想：在⊙O中任画一个圆周角∠BAC，圆心O与∠BAC可能会有几种位置关系？有3种位置关系.③证一证：∠BAC的一条边上时(如图1〕:∠BAC的内部时(如图2〕：作直径AD，同a，得.∠BAC的外部时(如图3〕.作直径AD,同a,得⑤归纳：一条弧所对的圆周角等于它所对的圆心角的一半.2.自学：学生可根据自学指导自主学习，相互交流.3.助学：〔1〕师助生：①明了学情：关注学生能否探究、归纳和证明圆周角定理.②差异指导：根据学情进行个别指导或分类指导.〔2〕生助生：小组内交流、研讨.4.强化：〔1〕圆周角定理的内容.〔2〕证明圆周角定理所表达的数学思想.〔3〕练习：如图，OA,OB,OC都是⊙O的半径，∠AOB=2∠BOC.求证：∠ACB=2∠BAC.证明：∵∠ACB=12∠AOB,∠BAC=12∠BOC,∠AOB=2∠BOC，∴∠ACB=2∠BAC.1.自学指导：〔1〕自学内容：教材第86页最后5行至第87页例4.〔2〕自学时间：10分钟.〔3〕自学方法：完成探究提纲.〔4〕探究提纲：①探究图中∠ACB ，∠ADB 和∠AEB 的数量关系.a.如图1，∵∠ACB=12∠AOB,∠ADB=12∠AOB,∠AEB=12∠AOB ，∴∠ACB = ∠ADB = ∠AEB.即同弧所对的圆周角 相等 .b.如图2，AB=AE,∵AB=AE,∴∠AOB = ∠AOE.∵∠ACB=12∠AOB, ∠ADE=12∠AOE, ∴∠ACB = ∠ADE. 即等弧所对的圆周角 相等 .c.由此可得，同弧或等弧所对的圆周角 相等 .d.练习：如图，点A 、B 、C 、D 在同一个圆上，四边形ABCD 的对角线把四个内角分成8个角，这些角中哪些是相等的角？∠1=∠4，∠2=∠7，∠3=∠6，∠5=∠8②半圆(或直径)所对的圆周角是 直角 ；90°的圆周角所对的弦是 直径 .为什么？因为半圆〔或直径〕所对的圆心角是180°，所以它所对的圆周角是90°，即直角.90°的圆周角所对的圆心角是180°，所以它所对的弦是直径.④ 如图，用直角曲尺检查半圆形的工件，哪个是合格的？为什么？第二个工件是合格的.因为半圆所对的圆周角为直角.④如图, ⊙O 的直径AB 为10cm,弦AC 为6cm, ∠ACB 的平分线交⊙O 于D,求BC ，BD 的长.∵AB 是直径，∴∠ACB=90°，∴在ACB Rt 中，（）BC AB AC cm =-=-=22221068. 同理∠ADB=90°，又CD 是∠ACB 的平分线，∴∠DCA=∠DCB=12∠ACB=45°, ∴∠DBA=∠DAB=45°,∴AD=BD.在ADB Rt 中，AD 2+BD 2=AB 2,∴BD AB cm ==21522. ⑤ 如图，你能设法确定一个圆形片的圆心吗？你有多少种方法？能，方法很多，例如：利用三角尺的直角可以找出两条直径〔90°的圆周角所对的弦是直径〕，两直径交点就是圆心.2.自学：学生可在自学指导的指引下自主学习，相互交流.3.助学：〔1〕师助生：①明了学情：关注学生是否会完成任务.②差异指导：根据学情进行个别指导或分类指导.〔2〕生助生：小组内交流、研讨.4.强化：〔1〕常规辅助线：遇直径，想直角.〔2〕点一名学生口答探究提纲中的问题②，点两名学生板演问题④，并点评.1.自学指导：〔1〕自学内容：教材第87页“思考〞到第88页“练习〞之前的内容.〔2〕自学时间：7分钟.〔3〕自学方法：阅读课文，完成自学参考提纲.〔4〕自学参考提纲：①什么叫圆内接多边形和多边形的外接圆？如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.②在图中标出BAD 和BCD 所对的圆心角，这两个圆心角有什么关系？∠BAD+∠BCD ＝ 180 度，同理可得：∠ABC+∠ADC ＝ 180 度.③圆内接四边形的性质：圆内接四边形的对角互补.④练习：a.如图，四边形ABCD为⊙O的内接四边形，∠BOD＝100°，那么∠BAD＝50°，∠BCD＝130° .b.如图，四边形ABCD内接于⊙∠B=110°，求∠ADE的度数.∵四边形ABCD内接于⊙O，∴∠B+∠ADC=180°，又∠ADC+∠ADE=180°，∴∠ADE=∠B=110°.c.求证：圆内接平行四边形是矩形.∵圆内接四边形对角互补，而平行四边形对角相等，∴圆内接平行四边形四个角都是直角.∴圆内接平行四边形是矩形.d.：如图，两个等圆⊙O1和⊙O2都经过A，B两点，经过点A的直线与两圆分别交于点C，D，经过点B的直线与两圆分别交于点E，F．假设CD∥EF，求证：四边形EFDC 是平行四边形.连接AB.∵四边形ABEC是⊙O1的内接四边形，∴∠C+∠ABE=180°.又∵四边形ABFD是⊙O2的内接四边形.∴∠D+∠ABF=180°.又∵∠ABE+∠ABF=180°.∴∠C+∠D=180°.∴CE∥DF.又∵CD∥EF，∴四边形EFDC是平行四边形.2.自学：学生可结合自学指导自主学习.3.助学：〔1〕师助生：①明了学情：明了学生自学提纲的答题情况.②差异指导：根据学情进行个别指导或分类指导.〔2〕生助生：生生互动，交流研讨.4.强化：〔1〕圆内接四边形的性质.〔2〕让学生完成自学参考提纲中的第④题，并点评.〔3〕练习：圆内接四边形ABCD中，∠A、∠B、∠C的度数的比是2∶3∶6，求四边形ABCD各内角的度数.解：∵∠A∶∠C＝2∶6,∠A+∠C＝180°,∴∠A＝45°，∠C＝135°.又∠A∶∠B＝2∶3,∴∠B＝67.5°，∠D＝180°-∠B＝112.5°.三、评价1.学生的自我评价〔围绕三维目标〕：这节课你学到了哪些知识？在哪些方面还感到比较困难？2.教师对学生的评价：〔1〕表现性评价：点评学生学习的态度、积极性、小组探究协作情况以及存在的问题等.〔2〕纸笔评价：课堂评价检测.3.教师的自我评价〔教学反思〕：〔1〕这节课首先是类比圆心角得出圆周角的概念.在探究圆周角与圆心角关系过程中，要求学生学会使用分类讨论以及转化的数学思想解决问题，同时也培养了学生勇于探究的精神.其次，本节课还学习了圆内接四边形定义及圆内接四边形的性质，通过例题和习题训练，可以使学生在解答问题时灵活运用前面的一些根底知识，从中获取成功的经验，建立学习的自信心.〔2〕圆周角定理的证明分了三种情况探讨，这里蕴含着重要的数学思想——分类思想，教材中多处闪烁着分类思想的光环:三角形分类、方程的分类等，故教学过程中要整理相互交融的知识结构，加强分类思想的渗透.(时间：12分钟总分值：100分)一、根底稳固〔80分〕1.(10分)以下四个图中，∠x是圆周角的是〔C〕2.(10分)如图,⊙O 中，弦AB 、CD 相交于E 点，且∠A=40°，∠AED=75°，那么∠B=〔D 〕A.15°B.40°C.5°D.35°3.(10分)如图，⊙O 的直径AB 与弦CD 垂直，且∠BAC=40°，那么∠BOD= 80° . 4.(10分)如图，点B 、A 、C 都在⊙O 上，∠BOA ＝110°，那么∠BCA＝ 125° .5.(10分)如图，⊙O 中，弦AD 平行于弦BC ，∠AOC=78°，求∠DAB的度数．解：∵AD ∥BC ，∴∠DAB=∠B.又∵∠B=12∠AOC=39°. ∴∠DAB=39°.6.(10分)如图，⊙O 的半径为1，A,B,C 是⊙O 上的三个点，且∠ACB=45°，求弦AB 的长.解：连接OA 、OB.∵∠BCA=45°,∴∠BOA=2∠BCA=90°.又OA=OB,∴△AOB 是等腰直角三角形.∴AB OA OB OA OA =+===222222.7.(10分)如图，A,P,B,C 是⊙O 上的四点，∠APC=∠CPB=60°，判断△ABC 的形状并证明你的结论.解：△ABC 是等边三角形.证明如下：∵∠APC=∠ABC=60°，∠CPB=∠BAC=60°，∴∠ACB=180°-∠ABC-∠BAC=60°，∴△ABC 是等边三角形.8.(10分)如图，A ，B ，C ，D 是⊙O 上的四点，延长DC ，AB 相交于点E ，假设BC=BE ．求证：△ADE 是等腰三角形．证明：∵∠A+∠BCD=180°,∠BCE+∠BCD=180°.∴∠A=∠BCE.∵BC=BE,∴∠E=∠BCE,∴∠A=∠E,∴AD=DE,∴△ADE是等腰三角形.二、综合应用〔10分〕9.(10分)如图，EF是⊙O的直径，把∠A为60°的直角三角板ABC的一条直角边BC 放在直线EF上，斜边AB与⊙O交于点P，点B与点O重合；将三角形ABC沿OE方向平移，使得点B与点E重合为止．设∠POF=x°，那么x的取值范围是30≤x≤60．三、拓展延伸〔10分〕10.(10分)如图，BC为半圆O的直径，点F是BC上一动点〔点F不与B、C重合〕，A是BF上的中点，设∠FBC=α，∠ACB=β．〔1〕当α=50°时，求β的度数;〔2〕猜想α与β之间的关系，并给予证明.解：〔1〕连接OA，交BF于点M.∵A是BF上的中点，∴OA垂直平分BF.∴∠BOM=90°-∠B=90°-α=40°.∴∠C=12∠AOB=12×40°=20°,即β=20°.〔2〕β=45°-1 2α.证明：由〔1〕知∠∠C＝β＝12∠AOB,∴β＝12〔90°-α〕＝45°-12α.三角形的稳定性【知识与技能】1.通知过观察、实践、想象、推理、交流等活动，让学生了解三角形具有稳定性，四边形没有稳定性，稳定性与没有稳定性在生产、生活中广泛应用.2.培养实事求是的学习作风和学习习惯.【过程与方法】1.通过提问、合作讨论以及小组交流方式探究三角形的稳定性.2.实物演示，激发学习兴趣，活泼课堂气氛.3.探究质疑，总结结果.和学生共同探究三角形稳定性的实例，答复课前提出的疑惑.【情感态度】1.引导学生通过实验探究三角形的稳定性，培养其独立思考的学习习惯和动手能力.2.通过合作交流，养成学生互助合作意识，提高数学交流表达能力.【教学重点】了解三角形稳定性在生产、生活中的实际应用.【教学难点】准确使用三角形稳定性于生产生活之中.一、情境导入，初步认识课前准备：木条〔用硬纸条代替〕假设干、小钉假设干、小黑板.问题1 工程建筑中经常采用三角形的结构，如屋顶钢架，钢架桥，其中道理是什么？问题 2 盖房子时,在窗框未安装好之前.木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢? 活动挂架为什么做成四边形？【教学说明】问题设立要让学生体会三角形在生产和生活中的应用，并引导思考为什么要在这些地方用三角形，另一些地方又要用到四边形.注意接纳学生其他不同的思路.教师讲课前，先让学生完成“自主预习〞.二、思考探究，获取新知老师演示P6探究内容，也可叫学生亲手实验，通过实际操作加深学生印象，完后请学生们交流讨论后答复得出了什么？教师根据学生们的答复进行简要归纳.【归纳结论】三角形木架形状不会改变，四边形木架形状会改变，这就是说，三角形具有稳定性，四边形没有稳定性.还可以发现，斜钉一根木条的四边形木架的形状不会改变.这是因为斜钉一根木条后，四边形变成了两个三角形，由于三角形有稳定性，窗框在未安装好之前也不会变形.三、运用新知，深化理解1.如图，一扇窗户翻开后，用窗钩BC可将其固定，这里所运用的几何原理是 .2.以下列图形中哪些具有稳定性?【教学说明】本节课的内容较少，题目比较简单，在学生独立完成后，要求学生说明理由.【答案】1.三角形具有稳定性.2.〔1〕〔4〕〔6〕中的图形具有稳定性.四、师生互动，课堂小结三角形具有稳定性，四边形没有稳定性.1.布置作业：从教材“习题”中选取.2.完成练习册中本课时的练习.本节课学习三角形稳定性，并板书课题.完成的教学目标是通过观察、实践、想象、推理、小组交流合作，使同学们了解三角形具有稳定性，四边形没有稳定性，稳定性与没有稳定性在生产、生活中广泛应用，培养同学们实事求是的学习作风和学习习惯，以及自主学习和独立思考的能力.。