金属晶体四种堆积模型空间利用率计算方法

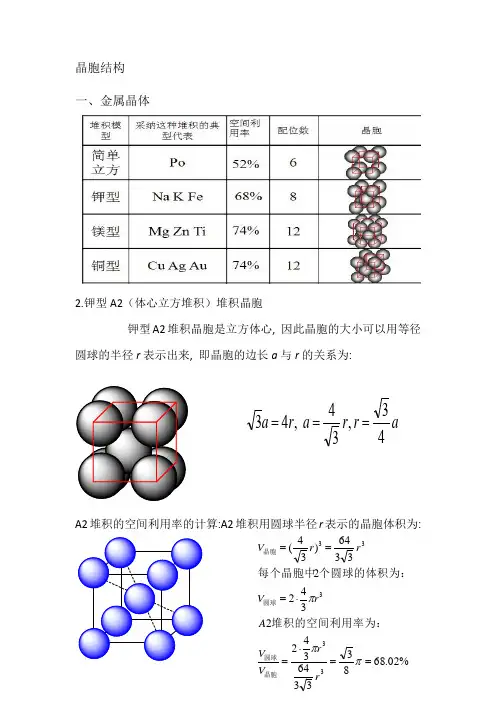
晶胞结构一、金属晶体2.钾型A2（体心立方堆积）堆积晶胞钾型A2堆积晶胞是立方体心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A2堆积的空间利用率的计算:A2堆积用圆球半径r 表示的晶胞体积为:ar r a r a 43,34 ,43===%02.68833364342234223364)34(33333==⋅=⋅===πππr r V V A rV rr V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中3.六方最密堆积（4）A1（面心立方最密堆积）A1是ABCABCABC······型式的堆积，从这种堆积中可以抽出一个立方面心点阵，因此这种堆积型式的最小单位是一个立方面心晶胞。

A1堆积晶胞是立方面心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A1堆积空间利用率的计算:A1堆积用圆球半径r 表示的晶胞体积为:（5）A4堆积形成晶胞A4堆积晶胞是立方面心点阵结构, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A4堆积的空间利用率的计算:A4堆积用圆球半径r 表示的晶胞体积为: ra r a 22 ,42==%05.742312163441344 4216)22(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中ar r a r r a 83,38 ,8243===⨯=%01.34163335123484348 833512)38(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中二、原子晶体1.金刚石立体网状结构，每个碳原子形成4个共价键，任意抽出2个共价键，每两个单键归两个六元环所有，而不是只归一个六元环所有（如图所示，红色的两个碳碳单键，可以构成蓝色和紫红色的两个六元环）。

晶胞的计算一、晶胞在高考中的地位分析：2008、2009年新课标，未对晶胞的计算进行考查；2010年新课标：37（4），一空，化学式的计算；2011年新课标：37（5），三空，晶胞中原子个数及密度的计算；2012年新课标：37（6），两空，晶胞密度、离子距离的计算。

二、常见的晶胞计算题：第一类：金属堆积方式的简单计算（空间利用率和密度）[选三P76] 晶胞密度 =m(晶胞)/V(晶胞)空间利用率=[V(球总体积)/V(晶胞体积)]×100%【注】1m＝10dm＝102 cm＝103 mm＝106 um＝109 nm＝1012 pm①简单立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：②体心立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：③面心立方最密堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：再假设该金属的摩尔质量为Mg/mol，N A为阿伏伽德罗常数的数值，试计算该晶胞的密度：【总结】必须掌握的常见晶胞及晶体结构分子晶体：干冰、冰晶胞图形、晶胞组成特点；原子晶体：金刚石（晶体硅）、二氧化硅晶胞组成特点、边长（体积、密度、原子最近距离）的计算方式；金属晶体：四种堆积方式的名称、图形、代表金属、边长（体积、密度、原子最近距离）的计算方式；离子晶体：NaCl、CsCl、CaF2晶胞图形、晶胞组成、边长（体积、密度、原子最近距离）的计算方式。

【练习】中学化学教材中展示了NaCl晶体结构，它向三维空间延伸得到完美晶体。

NiO(氧化镍)晶体的结构与NaCl 相同，Ni2+与最临近O2-的核间距离为 a cm，计算NiO晶体的密度(已知NiO的摩尔质量为74.7 g/mol)。

(2)天然和绝大部分人工制备的晶体都存在各种缺陷，例如在某氧化镍晶体中就存在如图所示的缺陷：一个Ni2+空缺，另有两个Ni2+被两个Ni3+所取代。

其结果为晶体仍呈电中性，但化合物中Ni 和O的比值却发生了变化。

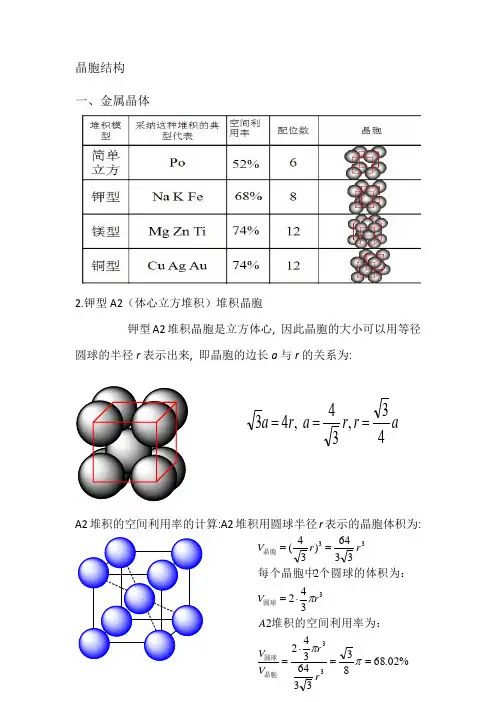
晶胞结构一、金属晶体2.钾型A2（体心立方堆积）堆积晶胞钾型A2堆积晶胞是立方体心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A2堆积的空间利用率的计算:A2堆积用圆球半径r 表示的晶胞体积为:ar r a r a 43,34 ,43===%02.68833364342234223364)34(33333==⋅=⋅===πππr r V V A rV rr V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中3.六方最密堆积（4）A1（面心立方最密堆积）A1是ABCABCABC······型式的堆积，从这种堆积中可以抽出一个立方面心点阵，因此这种堆积型式的最小单位是一个立方面心晶胞。

A1堆积晶胞是立方面心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A1堆积空间利用率的计算:A1堆积用圆球半径r 表示的晶胞体积为:（5）A4堆积形成晶胞A4堆积晶胞是立方面心点阵结构, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A4堆积的空间利用率的计算:A4堆积用圆球半径r 表示的晶胞体积为: ra r a 22 ,42==%05.742312163441344 4216)22(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中ar r a r r a 83,38 ,8243===⨯=%01.34163335123484348 833512)38(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中二、原子晶体1.金刚石立体网状结构，每个碳原子形成4个共价键，任意抽出2个共价键，每两个单键归两个六元环所有，而不是只归一个六元环所有（如图所示，红色的两个碳碳单键，可以构成蓝色和紫红色的两个六元环）。

晶胞的计算一、晶胞在高考中的地位分析：2008、2009年新课标，未对晶胞的计算进行考查；2010年新课标：37（4），一空，化学式的计算；2011年新课标：37（5），三空，晶胞中原子个数及密度的计算；2012年新课标：37（6），两空，晶胞密度、离子距离的计算。

二、常见的晶胞计算题：第一类：金属堆积方式的简单计算（空间利用率和密度）[选三P76]晶胞密度 =m(晶胞)/V(晶胞)空间利用率=[V(球总体积)/V(晶胞体积)]×100%【注】1m＝10dm＝102 cm＝103 mm＝106 um＝109 nm＝1012 pm①简单立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：②体心立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：③面心立方最密堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：再假设该金属的摩尔质量为Mg/mol，N A为阿伏伽德罗常数的数值，试计算该晶胞的密度：【总结】必须掌握的常见晶胞及晶体结构分子晶体：干冰、冰晶胞图形、晶胞组成特点；原子晶体：金刚石（晶体硅）、二氧化硅晶胞组成特点、边长（体积、密度、原子最近距离）的计算方式；金属晶体：四种堆积方式的名称、图形、代表金属、边长（体积、密度、原子最近距离）的计算方式；离子晶体：NaCl、CsCl、CaF2晶胞图形、晶胞组成、边长（体积、密度、原子最近距离）的计算方式。

【练习】中学化学教材中展示了NaCl晶体结构，它向三维空间延伸得到完美晶体。

NiO(氧化镍)晶体的结构与NaCl 相同，Ni2+与最临近O2-的核间距离为a cm，计算NiO晶体的密度(已知NiO的摩尔质量为74.7 g/mol)。

(2)天然和绝大部分人工制备的晶体都存在各种缺陷，例如在某氧化镍晶体中就存在如图所示的缺陷：一个Ni2+空缺，另有两个Ni2+被两个Ni3+所取代。

其结果为晶体仍呈电中性，但化合物中Ni 和O的比值却发生了变化。

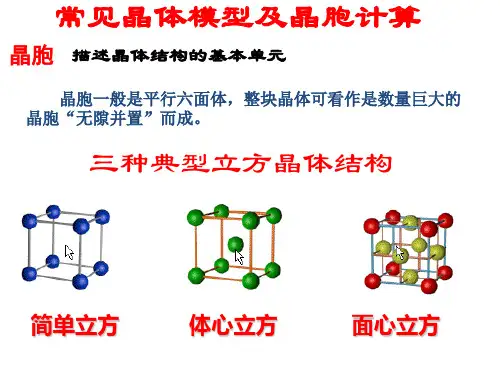
金属原子堆积的4种基本模式金属晶体可看成金属原子在三维空间中堆积而成。

、简单立方堆积：1不难理解，这种堆积方式形成的晶胞是一个立方体，每个晶胞含1个原子，被称为简单立方堆积。

这种堆积方式的空间利用率太低，只有金属钋(Po)采取这种堆积方式。

晶胞：一个立方体，1个原子，如金属钋。

、钾型2非密置层的另一种堆积方式是将上层金属原子填人下层的金属原子形成的凹穴中，每层均照此堆积，如图3—24所示。

与立方堆积相比空间利用率那一个高？晶胞：体心立方，两个原子。

如碱金属。

动手：把非密置层的小球黏合在一起，再一层一层地堆积起来，使相邻层的球紧密接触。

试一试，除了上述两种堆积方式外，是否可能有第三种方式?3、镁型和铜型密置层的原子按上述钾型堆积方式堆积，会得到两种基本堆积方式——镁型和铜型。

镁型如图3—25左所示，按ABABABAB……的方式堆积；铜型如图3—25右所示，按ABCADCABC……的方式堆积。

分别用代表性金属命名为镁型和铜型①，这两种堆积方式都是金属晶体的最密堆积，配位数均为12，空间利用率均为74％，但所得晶胞的形式不同。

金属晶体的两种堆积方式：b ei n ga 镁型：按ABABABAB……方式堆积；铜型：ABCADCABC……方式堆积；配位数均为12，空间利用率均为74％。

小结：金属晶体的四种模型对比：堆积模型采纳这种堆积的典型代表空间利用率配位数简单立方Po52％6钾型(bcp)Na 、K 、Fe 68％8镁型(hcp)Mg 、Zn 、Ti 74％12铜型(ccp)Cu 、Ag 、Au74％12。