金属晶体空间利用率计算97923-完整版
- 格式:pdf
- 大小:1.76 MB
- 文档页数:8


金属晶体晶胞中原子空间利用率的计算作者:李春文来源:《中学化学》2019年第01期金属晶体中原子堆积方式复杂,每种堆积中原子空间利用率不尽相同,掌握金属晶体里晶胞中原子空间利用率对于解决所有晶胞的原子空间利用率问题具有触类旁通的作用。
研究金属晶体里晶胞中原子空间利用率,首先应该掌握求算它的基本步骤:先找到晶胞中所含原子数,然后根据晶胞中紧邻原子的位置关系找到原子半径与晶胞边长的关系,再根据空间利用率的求算方法即晶胞中原子所占的实际体积与晶胞中原子围成的几何图形的体积之比,求得空间利用率。
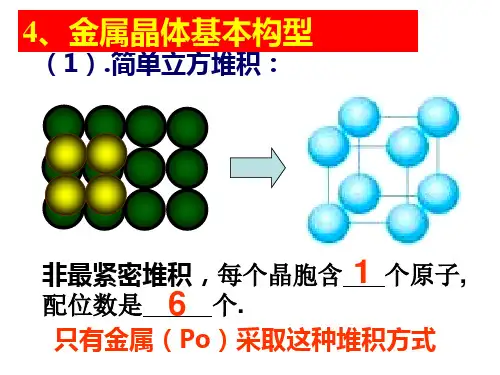
一、简单立方堆积简单立方堆积指的是相邻非密置层原子的原子核在同一直线,上的堆积。
这种堆积使晶胞结构为立方体型(如图1所示),处于顶点的两个原子紧邻。
晶胞中所含原子数为8x(1/8)=1,该原子所占的实际体积为(4/3)πr3。
由于处于顶点的两个原子紧邻,则原子半径与晶胞边长的关系为a=2r,那么晶胞中原子所围成的立方体的体积为(2r)3,所以简单立方堆积中原子空间利用率为二、体心立方堆积体心立方堆积指的是非密置层的另一种堆积方式,即将上层金属原子填人下层的金属原子形成的凹穴中,并使非密置层的原子稍稍分离。
每层均照此堆积,这种堆积方式称为体心立方堆积。
这种堆积方式使处于体对角线上的原子緊邻(如图2所示)。
晶胞中所含原子数为8x1/8+1=2,则晶胞中所含原子的实际体积为。
由于处于体对角线的原子紧邻,则原子半径与晶胞边长的关系为,所以体心立方堆积中原子空间利用率为三、六方最密堆积每层都是密置层堆积,堆积方式是将上层原子填入下层原子形成的凹穴中,这样的堆积会得到两种基本堆积方式,按ABABAB……的方式堆积称为六方最密堆积;按ABCABCA……的方式堆积称为面心立方最密堆积。
如图3所示,在六方最密堆积的晶胞结构中,体内原子位于平行六面体的一半的体心,即正三棱柱的体心,该原子与上下6个原子紧邻,则该原子与下面(或上面)3个原子构成正四面体结构。

常见晶体空间利用率的计算晶体空间利用率是晶格中原子或分子所占体积与晶胞体积之比。
它是描述晶体中原子或分子排列紧密程度的重要参数,对于研究晶体物理性质及合成新材料具有重要意义。
本文将介绍常见晶体空间利用率的计算方法。
晶体空间利用率的计算可以从两个角度出发:从输入晶体结构的角度,或者从晶胞的角度。
以下将分别对两种方法进行介绍。
1.从输入晶体结构的角度计算晶体空间利用率在这种方法中,需要输入晶体的原子或分子坐标,以及晶胞参数。
计算晶体空间利用率的一种常见方法是使用球形原子假设。
首先,计算晶胞中原子或分子的体积。
对于球形原子或分子,其体积可以通过球体积公式进行计算:V=4/3πr³,其中V为原子或分子体积,r为原子或分子的半径。
可以根据晶体结构中的原子或分子坐标,计算每个原子或分子的体积,并累加得到晶胞中原子或分子的总体积。
然后,计算晶胞的体积。
晶胞的体积可以通过晶胞参数计算得到。
对于立方晶胞,其体积可以简单地计算为晶胞参数的乘积。
对于其他类型的晶胞,可以使用相应的晶胞体积公式进行计算。
最后,将晶胞中原子或分子的总体积除以晶胞的体积,即可得到晶体的空间利用率。
2.从晶胞的角度计算晶体空间利用率在这种方法中,需要输入晶胞的晶胞参数,即晶胞的边长和角度。
首先,需要根据输入的晶胞参数,计算晶胞的体积。
对于正交晶体,晶胞的体积可以通过边长的乘积计算得到。
对于其他类型的晶胞,可以使用相应的晶胞体积公式进行计算。
然后,估算晶胞中原子或分子的体积。
可以使用球形原子假设,根据原子或分子的半径计算每个原子或分子的体积,并根据晶胞中的原子或分子数目进行累加,得到晶胞中原子或分子的总体积。
最后,将晶胞中原子或分子的总体积除以晶胞的体积,即可得到晶体的空间利用率。
需要注意的是,以上介绍的方法仅适用于球形原子或分子的情况。
对于非球形的原子或分子,空间利用率的计算更加复杂,需要考虑原子或分子间的相互作用、晶胞对称性等因素。


晶胞的空间利用率
空间利用率的计算公式:空间利用率=100%×球体积/晶胞体积。
空间利用率:指构成晶体的原子、离子或分子在整个晶体空间中所占有的体积百分比。
空间利用率的计算:
(1)计算晶胞中的微粒数。
(2)计算晶胞的体积。
一般情况下,晶胞都是平行六面体。
整块晶体可以看成是无数晶胞无隙并置而成的。
拓展资料
构成晶体的最基本的几何单元称为晶胞,其形状、大小与空间格子的平行六面体单位相同,保留了整个晶格的所有特征。
晶胞是能完整反映晶体内部原子或离子在三维空间分布之化学-结构特征的平行六面体最小单元。
其中既能够保持晶体结构的对称性而体积又最基本特称“单位晶胞”,但亦常简称晶胞。

金属晶体四类晶胞空间利用率的计算金属晶体四类晶胞空间利用率的计算高二化学·唐金圣在新课标人教版化学选修3《金属晶体》一节中,给出了金属晶体四种堆积方式的晶胞空间利用率。
空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。
下面就金属晶体的四种堆积方式计算晶胞的空间利用率。
一、简单立方堆积:在简单立方堆积的晶胞中,晶胞边长a等于金属原子半径r的2倍,晶胞的体积V晶胞=(2r)3。
晶胞上占有1个金属原子,金属原子的体积V原子=4πr3/3 ,所以空间利用率V原子/V晶胞 = 4πr3/ (3×(2r)3)=52.33﹪。
二、体心立方堆积:在体心立方堆积的晶胞中,体对角线上的三个原子相切,体对角线长度等于原子半径的4倍。
假定晶胞边长为a ,则a2 + 2a2 = (4r)2, a=4 r/√3 ,晶胞体积V晶胞 =64r3/ 3√3 。
体心堆积的晶胞上占有的原子个数为2,原子占有的体积为V原子=2×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(2×4πr3×3√3)/(3×64r3)= 67.98﹪。
三、面心立方最密堆积在面心立方最密堆积的晶胞中,面对角线长度是原子半径的4倍。
假定晶胞边长为a,则a2 + a2 = (4r)2 ,a = 2√2r ,晶胞体积V晶胞=16√2r3。
面心立方堆积的晶胞上占有的原子数为4,原子占有的体积为V原子 = 4×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(4×4πr3)/(3×16√2r3)= 74.02﹪.四、六方最密堆积六方最密堆积的晶胞不再是立方结构。
晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形,边长a = 2r ,夹角分别为60°、120°,底面积s = 2r×2r×sin(60°) 。



空间占有率计算公式
空间利用率的计算公式:空间利用率=100%×球体积/晶胞体积。
空间利用率:指构成晶体的原子、离子或分子在整个晶体空间中所占有的体积百分比。
空间利用率的计算:
(1)计算晶胞中的微粒数。
(2)计算晶胞的体积。
一般情况下,晶胞都是平行六面体。
整块晶体可以看成是无数晶胞无隙并置而成的。
构成晶体的最基本的几何单元称为晶胞,其形状、大小与空间格子的平行六面体单位相同,保留了整个晶格的所有特征。
晶胞是能完整反映晶体内部原子或离子在三维空间分布之化学-结构特征的平行六面体最小单元。
其中既能够保持晶体结构的对称性而体积又最基本特称“单位晶胞”,但亦常简称晶胞。

金属晶体四种堆积模型空间利用率计算方法(整理)
金属晶体四种堆积模型空间利用率计算方法(整理)2012-11-27 09:54阅读:
X
分享
我的博客微博
微信
朋友圈1
N
同时转发到微博
发送
借钱没面子手机借钱不求人
工薪族社保满半年即可申请1至15万
广告
我的更多文章
[转载]越秀区教研室网上的一篇让我很受启发的文章(原文过长,节选部分)
[转载]“五有四度”评课方法
[转载]把难度降下来
[转载]遇见“真正”的孩子──我们和“差生”
[转载]我们与差生
相关阅读
4加载中
你适不适合做会计测测就知道
免费测试 3分钟看清职业生涯
广告
打开疯狂捕鱼
海底宝藏等你探寻!
你来晒春节瞬间照,我们送千元大奖!。