金属晶体的空间利用率

金属晶体晶胞中原子空间利用率的计算作者：李春文来源：《中学化学》2019年第01期金属晶体中原子堆积方式复杂，每种堆积中原子空间利用率不尽相同，掌握金属晶体里晶胞中原子空间利用率对于解决所有晶胞的原子空间利用率问题具有触类旁通的作用。

研究金属晶体里晶胞中原子空间利用率，首先应该掌握求算它的基本步骤：先找到晶胞中所含原子数，然后根据晶胞中紧邻原子的位置关系找到原子半径与晶胞边长的关系，再根据空间利用率的求算方法即晶胞中原子所占的实际体积与晶胞中原子围成的几何图形的体积之比，求得空间利用率。

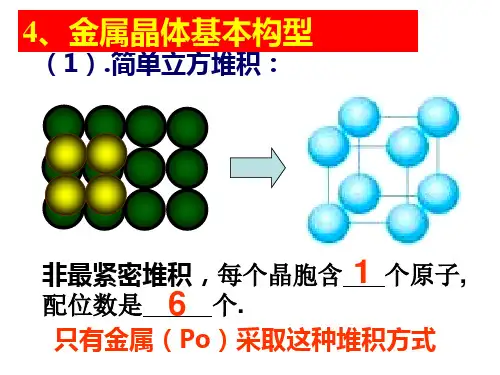
一、简单立方堆积简单立方堆积指的是相邻非密置层原子的原子核在同一直线，上的堆积。

这种堆积使晶胞结构为立方体型（如图1所示），处于顶点的两个原子紧邻。

晶胞中所含原子数为8x（1/8）=1，该原子所占的实际体积为（4/3）πr3。

由于处于顶点的两个原子紧邻，则原子半径与晶胞边长的关系为a=2r，那么晶胞中原子所围成的立方体的体积为（2r）3，所以简单立方堆积中原子空间利用率为二、体心立方堆积体心立方堆积指的是非密置层的另一种堆积方式，即将上层金属原子填人下层的金属原子形成的凹穴中，并使非密置层的原子稍稍分离。

每层均照此堆积，这种堆积方式称为体心立方堆积。

这种堆积方式使处于体对角线上的原子緊邻（如图2所示）。

晶胞中所含原子数为8x1/8+1=2，则晶胞中所含原子的实际体积为。

由于处于体对角线的原子紧邻，则原子半径与晶胞边长的关系为，所以体心立方堆积中原子空间利用率为三、六方最密堆积每层都是密置层堆积，堆积方式是将上层原子填入下层原子形成的凹穴中，这样的堆积会得到两种基本堆积方式，按ABABAB……的方式堆积称为六方最密堆积;按ABCABCA……的方式堆积称为面心立方最密堆积。

如图3所示，在六方最密堆积的晶胞结构中，体内原子位于平行六面体的一半的体心，即正三棱柱的体心，该原子与上下6个原子紧邻，则该原子与下面（或上面）3个原子构成正四面体结构。

金属晶体四类晶胞空间利用率的计算金属晶体四类晶胞空间利用率的计算高二化学·唐金圣在新课标人教版化学选修3《金属晶体》一节中，给出了金属晶体四种堆积方式的晶胞空间利用率。

空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。

下面就金属晶体的四种堆积方式计算晶胞的空间利用率。

一、简单立方堆积：在简单立方堆积的晶胞中，晶胞边长a等于金属原子半径r的2倍，晶胞的体积V晶胞=(2r)3。

晶胞上占有1个金属原子，金属原子的体积V原子=4πr3/3 ，所以空间利用率V原子/V晶胞 = 4πr3/ （3×(2r)3）=52.33﹪。

二、体心立方堆积：在体心立方堆积的晶胞中，体对角线上的三个原子相切，体对角线长度等于原子半径的4倍。

假定晶胞边长为a ，则a2 + 2a2 = (4r)2， a=4 r/√3 ，晶胞体积V晶胞 =64r3/ 3√3 。

体心堆积的晶胞上占有的原子个数为2，原子占有的体积为V原子=2×（4πr3/3）。

晶胞的空间利用率等于V原子/V晶胞 =（2×4πr3×3√3）/（3×64r3）= 67.98﹪。

三、面心立方最密堆积在面心立方最密堆积的晶胞中，面对角线长度是原子半径的4倍。

假定晶胞边长为a,则a2 + a2 = (4r)2 ,a = 2√2r ,晶胞体积V晶胞=16√2r3。

面心立方堆积的晶胞上占有的原子数为4，原子占有的体积为V原子 = 4×（4πr3/3）。

晶胞的空间利用率等于V原子/V晶胞 =（4×4πr3）/(3×16√2r3)= 74.02﹪.四、六方最密堆积六方最密堆积的晶胞不再是立方结构。

晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形，边长a = 2r ,夹角分别为60°、120°，底面积s = 2r×2r×sin(60°) 。

选修3第三章《晶体结构与性质》单元测试题选择题（每小题只有一个正确答案。

每小题3分，共45分）1.下列有关金属晶体的判断正确的是A．简单立方、配位数6、空间利用率68% B．钾型、配位数6、空间利用率68% C．镁型、配位数8、空间利用率74% D．铜型、配位数12、空间利用率74% 2.有关晶格能的叙述正确的是A．晶格能是气态离子形成1摩离子晶体释放的能量B．晶格能通常取正值，但是有时也取负值C．晶格能越大，形成的离子晶体越不稳定D．晶格能越大，物质的硬度反而越小3.下列排列方式是镁型堆积方式的是A．ABCABCABC B．ABABABABAB C．ABBAABBA D．ABCCBAABCCBA 4.下列关于粒子结构的描述不正确的是A．H2S和NH3均是价电子总数为8的极性分子B．HS－和HCl均是含一个极性键的18电子粒子C．CH2Cl2和CCl4均是四面体构型的非极性分子D．1 mol D162O中含中子、质子、电子各10 N A(N A代表阿伏加德罗常数)5.现代无机化学对硫－氮化合物的研究是最为活跃的领域之一。

其中如图所示是已经合成的最著名的硫－氮化合物的分子结构。

下列说法正确的是A．该物质的分子式为SNB．该物质的分子中既有极性键又有非极性键C．该物质具有很高的熔沸点D．该物质与化合物S2N2互为同素异形体6.某物质的实验式为PtCl4·2NH3，其水溶液不导电，加入AgNO3溶液反应也不产生沉淀，以强碱处理并没有NH3放出，则关于此化合物的说法中正确的是A．配合物中中心原子的电荷数和配位数均为6B．该配合物可能是平面正方形结构C．Cl—和NH3分子均与Pt4+配位D．配合物中Cl—与Pt4+配位，而NH3分子不配7.石墨能与熔融金属钾作用，形成石墨间隙化合物，钾原子填充在石墨各层谈原子中。

比较常见的石墨间隙化合物是青铜色的化合物，其化学式可写作CxK,其平面图形见下图，则x值为:A . 8 B. 12 C.24 D.608.金属键具有的性质是A．饱和性B．方向性C．无饱和性和方向性D．既有饱和性又有方向性9.下列说法正确的是A．124g P4含有的P－P键的个数为6N A B．12g石墨中含有的C－C键的个数为2N A C．12g金刚石中含有的C－C键的个数为1.5N A D．60gSiO2中含Si－O键的个数为2N A 10.长式周期表共有18个纵行，从左到右排为1－18列，即碱金属为第一列，稀有气体元素为第18列。

面心立方和体心立方与金属密度的关系
【实用版】
目录
1.面心立方和体心立方的定义与特点
2.面心立方和体心立方金属的密度比较
3.影响金属密度的因素
4.总结
正文
面心立方和体心立方是两种常见的晶体结构，它们在金属材料中有着广泛的应用。

在这篇文章中，我们将探讨面心立方和体心立方与金属密度的关系。

首先，我们来了解一下面心立方和体心立方的定义与特点。

面心立方晶体中，金属原子分布在立方体的八个角上和六个面的中心，其空间利用率为 74.05%，配位数为 12。

而体心立方晶体中，八个原子处于立方体的角上，一个原子处于立方体的中心，其空间利用率为 68.2%，配位数为 8。

接下来，我们来比较一下面心立方和体心立方金属的密度。

根据晶胞的原子数、配位数和致密度，我们可以得出面心立方金属的密度比体心立方金属的密度大。

具体来说，面心立方金属的密度为 74.05%，而体心立方金属的密度为 68.2%。

因此，在相同体积的情况下，面心立方金属的质量要比体心立方金属的质量大。

影响金属密度的因素有很多，例如原子大小、原子间距、空间利用率等。

在这些因素中，空间利用率对金属密度的影响最大。

由于面心立方晶体的空间利用率比体心立方晶体高，所以面心立方金属的密度也比体心立方金属的密度大。

总之，面心立方和体心立方是两种不同的晶体结构，它们在金属材料
中的应用也有所不同。

面心立方金属的密度比体心立方金属的密度大，这主要是由于面心立方晶体的空间利用率比体心立方晶体高。