四面体网格上的Lagrange插值

%拉格朗日插值方法%可以同时对多点插值%t可以为向量function s=lag(x,y,t)%采用符号推导，这样可以给出插值具体公式syms p;%读取x向量维数n=length(x);s=0;for(k=1:n)la=y(k);%构造基函数for(j=1:k-1)la=la*(p-x(j))/(x(k)-x(j));end;for(j=k+1:n)la=la*(p-x(j))/(x(k)-x(j));end;s=s+la;simplify(s);end%对输入参数个数做判断，如果只有两个参数%直接给出插值多项式%如果三个参数则给出插值点的插值结果%第三个参数可以为向量if(nargin==2)s=subs(s,'p','x');%展开多项式s=collect(s);%把系数取到6位精度表达s=vpa(s,4);else%读取t长度m=length(t);%分别对t的每一个分量插值for i=1:mtemp(i)=subs(s,'p',t(i));end%得到的是系列插值点的插值结果%既得到的是向量，赋值给ss=temp;end%lagrange方法主函数%同时计算多点插值%已有点x ，yx=[pi/4,pi/6,pi/3,pi/2];y=[cos(pi/4),cos(pi/6),cos(pi/3),cos(pi/2)];%需要插值点t=[-40*pi/180,47*pi/180,53*pi/180,79*pi/180,174*pi/180]; disp('角度')du=[-40 47 53 79 174]%插值计算结果disp('插值结果')yt=lag(x,y,t)%cos函数值disp('cos函数值')yreal=[cos(-40*pi/180)cos(47*pi/180)cos(53*pi/180)cos(79*pi/180)cos(174*pi/180)]'disp('插值与函数值误差')dy=yt-yreal%给出插值多项式，需要显示的话去掉下行的分号yt=lag(x,y)%画出插值多项式图形ezplot(yt,[-pi/4,pi])hold on%画出cos函数图形ezplot('cos(t)',[-pi/4,pi]);grid onhold off。

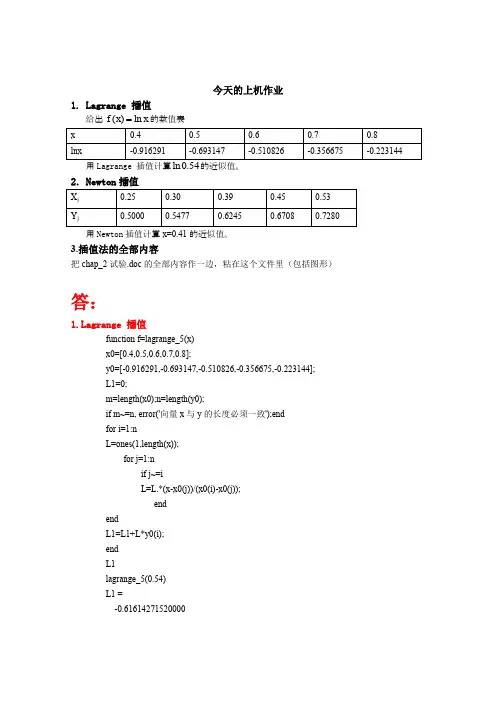
今天的上机作业1. Lagrange 插值给出()ln f x x 的数值表用Lagrange 插值计算ln 0.54的近似值。

2．Newton 插值用Newton 插值计算x=0.41的近似值。

3.插值法的全部内容把chap_2试验.doc 的全部内容作一边，粘在这个文件里（包括图形）答：grange 插值function f=lagrange_5(x) x0=[0.4,0.5,0.6,0.7,0.8];y0=[-0.916291,-0.693147,-0.510826,-0.356675,-0.223144]; L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x 与y 的长度必须一致');end for i=1:nL=ones(1,length(x)); for j=1:n if j~=iL=L.*(x-x0(j))/(x0(i)-x0(j)); end endL1=L1+L*y0(i); end L1lagrange_5(0.54) L1 =-0.616142715200002．Newton插值function f=newton_li5(x) %x0为入的节点值，y0相应节点的函数值x0=[0.25 0.30 0.39 0.45 0.53];y0=[0.5000 0.5477 0.6245 0.6708 0.7280];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)Hxnewton(0.41)n =5hx =0.64030542443064ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.948930296755483.插值法的全部内容把chap_2试验.doc的全部内容作一边，粘在这个文件里（包括图形）P28 例22点插值function f=lagrange_2(x)x0=[0.32,0.34];y0=[0.314567,0.333487];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_2(0.3367)L1 =0.330365200000003点插值function f=lagrange_3(x)x0=[0.32,0.34,0.36];y0=[0.314567,0.333487,0.352274];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_3(0.3367)L1 =0.33037436203750Lagrange插值法%eg1_lagr.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=lagr1(x1,y1,xx); %2次插值chazhi_y45_2=lagr1(x1,y1,4.5);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=lagr1(x2,y2,xx); %4次插值chazhi_y45_4=lagr1(x2,y2,4.5);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=lagr1(x3,y3,xx); %8次插值chazhi_y45_8=lagr1(x3,y3,4.5);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on计算函数值function f=newton_li4(x) %x0为入的节点值，y0相应节点的函数值x0=[0.40,0.55,0.65,0.80,0.90,1.05];y0=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)hxnewton(0.596)n =5hx =0.77193768707246ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.94893029675548Newton插值法%eg1_newton.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=newton1(x1,y1,xx,2); %2次插值chazhi_y45_2=newton1(x1,y1,4.5,2);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=newton1(x2,y2,xx,4); %4次插值chazhi_y45_4=newton1(x2,y2,4.5,4);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=newton1(x3,y3,xx,8); %8次插值chazhi_y45_8=newton1(x3,y3,4.5,8);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on。

数学基础课里的lagrange插值公式lagrange插值公式：
1. Lagrange插值法是一种经典的插值方法，在数学和工程领域里都是一种常用的数值算法，也可以用来求解一元函数的极值点。

它实际上是对有n个数据点（比如：xi，yi）的函数f ( x) 进行拟合，形成n-1阶有理曲线，使得拟合曲线经过这些数据点。

2. Lagrange插值公式的可求性：在n个点的插值中，已知n个数据点（xi，yi），求使拟合曲线恰
好经过n个点的系数 ak 的问题。

3. Lagrange 插值公式：向量f (x) 和向量自变量x 可定义如下：f (x) = (f1 (x)，f2 (x)，…，fn-1 (x)，fn (x))；xi = (x1，x2，…，xn)，那么有f (x) = Σ
j=1 n Lj(x).fj (*j = 1, 2,…, n*)
（其中Lj (x) 为Lagrangebasis 的基函数，可定义为：Lj (x) =Π(x/xj, i !=j)）
4. Lagrange 插值公式的优点：
(1) Lagrange插值法简单易懂，实现简单；
(2) Lagrange插值法的拟合精度高；
(3) Lagrange插值法的拟合速度也是很快的，适用
性强。

5. Lagrange 插值公式的缺点：
(1) Lagrange插值法拟合数据点多时，计算量大；
(2) Lagrange插值法只适用于有n个数据点的插值，不能求解多元插值。

四面体框架上的Lagrange插值崔利宏;张丰利;铁旭【摘要】在以往研究二元函数Lagrange插值的基础上,对四面体框架上的三元Lagrange插值结点组可解性问题进行了研究.给出了构造四面体框架上三元Lagrange插值可解结点组的迭加构造方法以及利用可解结点构造三元多项式空间上的插值多项式的方法,搞清了四面体框架上的Lagrange插值可解结点组的某些基本理论和拓扑结构.所得构造方法都是以迭加方式来实现的,这对于编译计算机算法程序,进而在计算机上自动完成插值可解结点组的构造并得到插值格式创造了十分便利的条件.最后给出了实例验证算法的有效性.【期刊名称】《辽宁师范大学学报（自然科学版）》【年(卷),期】2016(039)001【总页数】6页(P1-6)【关键词】四面体框架;多元Lagrange插值;空间平面插值;空间直线插值;可解结点组【作者】崔利宏;张丰利;铁旭【作者单位】辽宁师范大学数学学院,辽宁大连116029;辽宁师范大学数学学院,辽宁大连116029;辽宁师范大学数学学院,辽宁大连116029【正文语种】中文【中图分类】O174.41函数插值是计算数学以及计算机辅助设计几何设计的重要工具，当前，随着电子计算机技术的不断进步，函数插值尤其是多元函数插值的理论以及应用研究得到迅速的发展和广泛的应用．例如:多元函数插值在CT成像技术，计算机图像处理等研究领域有着十分重要的作用，同时在曲面外形设计，多元函数列表和有限元法等领域的应用就更加广泛［1］．1953年，I．Schoenberg等人得到了判断一元样条函数插值结点组是否为可解结点组的准则，即著名的Schoenberg-Whitney定理．有了完整的函数插值与逼近理论之后，函数插值与逼近无论在理论研究还是在应用问题讨论方面都更加方便．此后，关于函数插值的理论以及应用的研究不断取得进展．特别是随着计算机技术的飞速发展，人们进一步认识到多项式函数(包括样条函数)所具有的计算方便性以及局部可调的灵活性，易存储性等诸多性质的重要意义，并把它应用到与科学计算相关的许多领域，比如数值逼近，微分方程数值解，计算辅助几何设计，小波及有限元等［2-4］．同时，多元函数插值和逼近理论在各个方面的推广也成为数学工作者密切关注并深入研究的重要课题．在以往有关多元函数插值基本理论和方法基础上，对四面体框架上的三元函数Lagrange插值结点组的可解性问题进行了研究和探讨．因为在进行三元函数Lagrange插值时，一个首先必须解决的问题就是插值函数的唯一存在性问题，而这一问题的决定因素就是插值结点组的几何拓扑结构．首先给出三元Lagrange插值问题提法和定义．设n为非负整数并且代表所有全次数不超过n的三元实系数多项式空间，即定义1．1［6］设是中的dn个相异点．对于一个任意给定的实数组，寻找一个多项式使之满足如下插值条件如果对于每一个任意给定的实数组，方程组(1)总存在唯一一组解，则称该插值问题是关于多项式空间的唯一可解插值问题，并称相应的插值结点组为关于多项式空间的插值唯一可解结点组．定理1．1［7］中的dn个相异点能够做成中的一个n次插值唯一可解结点组的充要条件是不落在中任何一个n次代数曲面上．由定理1．1知，在瓗3中关于多项式空间进行插值时，插值结点组一定不能位于同一个代数曲面上，否则将会导致插值问题不适定．但在实际问题中，如调和分析，曲面上的散乱数据插值与拟合等，常常需要考虑插值结点位于同一代数曲面上(更广泛地讲，乃至同一代数流形上)的情况．本文只涉及空间平面上的情形．定义1．2 设q(X)=0为一个空间平面．定义dn'如下:寻找一个多项式g()设为q(X)=0上的dn'个相异点，对于一个任意给定的实数组X∈Ρ()为空间平面q(X)=0上的n次插值可解结点组．空间平面上的插值可解结点组的拓扑结构与空间直线上的插值可解结点组密切相关．下面给出空间直线上Lagrange插值概念．定义1．3 设空间两平面p(X)=0与q(X)=0相交于空间直线C=s(p，)3如果对于每一个任意给定的实数组n，使之满足如下插值条件，方程组(3)总存在一组解，则称结点组q．定义en(空间直线上的en个相异点所构成的点组，对于一个任意给定的实数组上的n次插值多项式空间维数)如下设为空间直线，寻找一个多项式上的n次插值可解结点组．主要结果如下:定理1．2(构造三元多项式空间插值唯一可解结点组的四面体迭代法)．在三维空间上做4个平面πi(i=1，2，3，4)使其交成一个四面体，如图1．在四面体的6个边上分别取异于顶点的n－1个互异点，再在每个平面πi(i=1，2，3，4)上(但不在6条边上)取沿该平面的n－3次插值可解结点组记为Αi，则有:(i)Αi加上平面πi所在3条边中任意1条边上的n－1个互异点一起必定构成沿平面πi的n－2次插值可解结点组;(ii)Αi加上平面πi所在3条边中任意2条边上的n－1个互异点再加上所在三角形任意2个顶点，，使之满足如下插值条件为空间直线如果对于每一个任意给定的实数组，方程组(4)总存在一组解，则称结点组则这些点必定构成沿平面πi的n－1次插值可解结点组;(iii)Αi加上平面πi所在3条边上全部n－1个互异点再加上所在三角形的3个顶点，则这些点必定构成沿平面πi的n次插值可解结点组．如果用μi表示平面πi上所取的沿该平面的n－3次插值可解结点组加上其所在三角形3个边上所取的n－1个点以及三角形的3个顶点共同组成的点集，则有:定理1．3若表示在四面体之外关于的一个n－4次插值唯一可解结点组，则必定构成的插值唯一可解结点组，而点组也都是的插值唯一可解结点组．能够做成q(X)=0的n次插值可解结点组的充要条件是，对于任何一个满足零插值条件:g(Qi)=0，i=1，…，dn'的多项式引理1［8］设dn'为式(2)所定义，则位于空间平面q(X)=0上的点组，均存在如下分解:g(X)=q(X)r(X)．其中，当n≥k时，而当n＜k时，r(X)=0．引理2［9］设en为式(4)所定义，空间两平面p(X)=0与q(X)=0相交于空间直线C=s(p，) q．则位于的n次插值可解结点组的充要条件是，对任何满足零插值条件g(Qi)=0，i=1，…，en的多项式，均存在如下形式的分解:上的点组能够做成引理3［5］设的一个插值适定结点组，做一个k次无重复分量代收曲面q(X) =0，使其不通过Α中任何点．任取沿曲面q(X)=0上的一个n+k次插值适定节点组B，则Α∪Β必定构成空间的插值适定结点组．引理4［5］假设k次代数曲面q(X)=0与平面h(X)=0相交于一个平面代数曲线C=s(q， h)(这里s(q，h)表示多项式q(X)与h(X)的公共零点集)．如果为沿曲面q(X)=0的一个n次插值适定结点组，Α不位于曲线C=s(q，h)上．在曲线C=s(q，h)上任取一个沿该曲线的n +1次插值适定结点组，则Α∪Β必定构成沿曲面q(X)=0的一个n+1次插值适定结点组，即是沿平面π1的n－3次插值适定结点组．对于且．因为Α构成沿交线上的n－ 2次插值适定结点组，且，则由引理2可知又因为，则所以有由于Α1是沿平面π1的n－3次插值适定结点组，β为n－3次多项式，则由引理1知，将式(6)代入式(5)有定理1．2证完．定理1．3的证明由于是的插值可解结点组，而Αi为平面πi上的n－3次插值可解结则Α构成沿交线上的n－2次插值适定结点组．设定理1．2的证明先证(i)其余类似．不妨取i=1，在AD边上取n－1个点为点组，由引理3知必定构成的插值唯一可解结点组，接下来使用定理1．2中(i)的方法，可以得到平面上的一个n－2次插值可解结点组记为Αj，则有必定构成的插值唯一可解结点组，重复上述过程，并继续使用定理1．2中(ii)，(iii)中方法有必定构成的插值唯一可解结点组，而且容易验证所含点恰好与所含点相同，均为个点等于的维数．定理1．3证完．注记1．1 由定理1．1和定理1．2有:设f(x，y，z)为被插值函数分别是函数f(x，y， z)在中关于结点组βi(i=1，2，3，4)的插值多项式．其中，(xi，yi，zi)(i=1，2，3，4)为平面li(i=1，2，3，4)所对应的四面体的顶点坐标，则是f(x，y，z)在中关于结点组的插值多项式．并且有如下构造算法:设四面体ABCD4个面ABC，BCD，ABD和ACD的方程分别为:用4簇平行平面:将四面体作等距剖分，用Qijk表示ai(x，y，z)=0，bj(x，y，z)=0与ck(x，y，z)=0的交点，则瓘n={Qijk|k=0，1，…，n－i－j;j=0，1，…，n－i;i=0，1，…，n}构成Ρn的插值唯一可解结点组．令:则对应点Qijk的Lagrange插值基本多项式为:从而得到上面的Lagrange插值公式如下:下面给出定理的算例．例求函数f(x，y，z)=ex+y+z在如图2所示四面体上的插值多项式．解图2四面体各顶点坐标为:函数f(x，y，z)=ex+y+z在以上各点的函数值分别为:令则构成空间的插值唯一可解结点组．构成的插值唯一可解结点组．使用Matlab计算求得:且，分别带入得插值多项式:用Matlab做出被插值函数f(x，y，z)和所求多项式Ρ2(x，y，z)在z=1平面上的投影为图3所示．经Matlab计算求得，而，插值误差小于0．3．【相关文献】［1］MARIANO Gasca，THOMASSauer．On the history ofmultivariate polynomial interpolation［J］．Journal of Computional and Applied Mathematics，2000，122:23-35．［2］AHLIN A C．A bivariate generalization of Hermites interpolation formula ［J］．Math Compute，1964，18:264-273．［3］周蕴时，苏志勋，奚涌江，等．CAGD中的曲线和曲面［M］．长春:吉林大学出版社，1993:21-151．［4］CHUNG K C，YAO T H．On lattices admitting unique Lagrange interpolation ［J］．SIAM JNumer Anal，1977，14:735-741．［5］梁学章，李强．多元逼近［M］．北京:国防工业出版社，2005:21-37．［6］LIANG X Z．Lagrange representation ofmultivariate interpolation［J］．Science inChina，1989，32(4):385-396．［7］崔利宏，李笑笑，高小凇，等．二元四次切触插值格式的构造方法［J］．辽宁师范大学学报(自然科学版)，2014，37(2):145-148．［8］WARRE J．Blending algebraic surfaces［J］．ACM Transaction on Graphics，1989，8(4):263-278．［9］梁学章，朱功勤．构造二元切触插值公式的方法［J］．数学研究与评论，1981(1):91-100．［10］梁学章，二元插值的适定结点组与迭加插值法［J］．吉林大学学报(自然科学版)，1979(1):27-32［11］徐利治，王仁宏，周蕴时．边界型求积公式的构造方法及应用［J］，计算数学，1978(3):54-76．。