专升本工程力学第5章 弹性变形体静力分析基础
- 格式:ppt
- 大小:999.00 KB
- 文档页数:15

《建筑力学》课程教学大纲一、本课程的地位、作用和任务《建筑力学》是水利水电建筑工程专业的一门重要的专业基础课,在本专业中起着承上启下的作用,为后续课程打基础。
《建筑力学》的任务是:教授学生掌握物体受力分析与静力平衡问题的求解方法;杆件及结构内力与变形的分析方法;关于构件的强度、刚度与稳定性的计算及构件应力、应变的方法。
通过本课程的学习,要求学生具备对常见结构、构件进行受力分析、内力与变形计算的能力,并初步具备对结构的实验分析能力。
二、教学内容和教学要求第一章绪论1、教学内容建筑力学的研究对象、研究方法、主要内容。
2、教学要求了解建筑力学课程的性质、地位和作用,了解建筑力学各部分的内容、了解建筑力学的学习方法。
第一篇、静力学第二章刚体静力分析基础1、教学内容2—1 力与力偶1)力的概念和性质2)力对点之矩3)力偶的概念和性质2—2 约束与约束反力1)约束与约束反力的概念2)工程中常见的约束与约束反力2—3 受力分析与受力图2、教学要求(1)理解力、力对点的矩、平面力偶的概念及静力学的四个公理,合力矩定理、刚体的概念;掌握平面力偶系合成的计算。
(2)了解约束的概念及荷载的分类;了解作用在构件上荷载的计算方法;掌握常见工程中的约束类型及其约束反力的确定;第三章平面力系1、教学内容3—1 平面力系向一点的简化1)力的平移定理2)平面力系向一点的简化3)力在坐标轴上的投影主矢与主矩的计算4)平面力系向一点简化结果的进一步分析3—2 平衡方程及其应用1)平面一般力系的平衡条件和平衡方程2)平面力系的几种特殊情形3)静定与超静定问题4)物体系的平衡问题2、教学要求(1)了解力的平移定理的内容;掌握力在坐标轴上的投影的概念及计算,掌握合力的投影定理;(2)理解平面一般力系的概念;了解平面一般力系向一点简化和简化结果分析。
(3)掌握平面一般力系、平面汇交力系、平面平行力系及平面力偶系的平衡方程及其应用,重点掌握常见物体支座反力的求法。





第5章弹性静力学小位移变形理论的变分原理(16K)资料.doc第5章弹性静力学小位移变形理论的变分原理对连续体来说,其数学上的处理方法是利用给定的边界条件下的微分方程(或偏微分方程),并在一定的边界条件下求得其解,这种解析方法,实际做起来往往遇到很大的困难,使许多工程实际问题的计算模型很难建立,满足不了实际需要。自从五十年代直刚法问世以来,利用离散化的方法,将一个连续体划分为有限数量及具有一定几何形状的单元体,即有限单元,再按照一定的过程进行计算,这就使得过去许多工程计算感到困难的问题得到解决,这种方法不受结构特殊几何形状的限制,因此,它的适应范围是相当广泛的。有限元素法的提出和应用,是工程分析方法上的一次重大的变革,随着理论探讨上的深入及计算机性能的不断提高,使得解的精确性不断地得到改进,以至使得有限元素法成为当前计算领域方面的一个强有力的工具,无论对结构问题(如静力学、动力学)、非结构问题(如流体力学、光学、电磁学)以及许多边缘学科等都得到广泛的应用。有限元素法的解题过程和步骤在一般的有关有限元法教课书和著作中均有详细讨论,本章不再赘述。- 53 -- 54 -变分原理是有限元素法的基础,要很好地理解有限元素法,则应该对能量变分原理有一个较系统地了解。本章的目的是尽可能地对这些能量变分原理作系统性的介绍,从一般常用的最小位能原理和最小余能原理,引深到引用拉格朗日乘子法(Lagrange Multiple Method)的完全及不完全广义变分原理和为分区集合体的分区(Sub-region)广义变分原理,这将涉及到以混合(Mixed)模型和杂交(Hybrid)模型为基础的变分原理。在此基础上,针对不同变分原理,进一步说明了有限元素法中的元素的刚度特性和推导元素刚度矩阵的一般过程及表达显式,以及变分原理在结构分析中的若干应用实例,使读者能比较清晰地了解各类变分原理与建立有限元模型之间的关系。§5.1 小位移弹性理论的最小位能原理与最小余能原理设在卡氏直角坐标系中,坐标参数为)3,2,1(=i x i ,体积为V 的弹性体中任意一点的位移参数为)3,2,1(=i u i 、应力分量为ij σ以及应变分量为)3,2,1,(=εj i ij 。由线弹性力学理论,我们可以得到如下的用于描述一个弹性静力学小位移变形问题的基本方程式。(1)力的平衡方程0,=+σij ij F (在V 内) (5-1)- 55 - 式中i F 表示体力,j ij ,σ表示应力分量ij σ对坐标分量j x 的偏导数(以下相同)。(2)应变位移关系式(几何关系))(21,,ij j i ij u u +=ε (在V 内) (5-2) (3)应力应变关系式(物理关系)kl ijkl ij a ε=σ (5-3) kl ijkl ij b σ=ε (5-3’) 式中ijkl a 为弹性模量系数,ijkl b 为劲度系数,ijkl a 和ijkl b 都具有对称性。 (4)在弹性体的边界上,表面S 可划分为两部分:外力已知的边界σS 及位移为已知的边界u S ,前者称为力的边界,后者称为位移边界,即u S S S +=σ (5-4)在力的边界σS 上,i j ij T n =σ (5-5) 式中i T 为已知边界力,j n 为σS 的边界外法线向量与坐标轴夹角的方向余弦。在位移边界u S 上,i i u u = (5-6) 式中i u 为已知边界位移。(5-5)式和(5-6)式统称为“边界条件”。上述的诸方程共有15个,即3个平衡方程,6个应变位移关系方程,6个物理关系方程。而未知变量也共计15个:6个应力分量ij σ,6个应变分量ijε和3个位移分量iu 。因此该问题是可以求解的。- 56 -小位移变形弹性体的应变能泛函(或应变能密度)A 和余应变能泛函(余应变能密度)B 可表示为klij ijkl ij a A εε=ε21)( (5-9) kl ij ijkl ij b B σσ=σ21)( (5-10) 不难看出,)(ij A ε和)(ij B σ有以下关系,)()(ij ij ij ij B A σ+ε=σε (5-11)并且容易证明ij ij ij B σ∂σ∂=ε)( (5-12) ij ij ij A ε∂ε∂=σ)( (5-13) (一)虚功原理与总位能原理这里用ij εδ和i u δ分别表示应变变分和位移变分,在虚功原理中可视为虚应变和虚位移。则由虚功原理可写出虚功方程为0dS δdV δd δV i =--εσ⎰⎰⎰σS ii i V ij ij u T u F V (5-14) (5-14)式成立是有条件的,要求ij εδ和i u δ在弹性体内部满足应变位移关系和在位移边界上满足给定位移边界条件,即)δδ(21δ,,ij j i ij u u +=ε (在V 内) (5-15a) 0δ=i u (在u S 上) (5-15b)虚功原理表明,如果弹性体在给定的体力和边界力作用下处于平衡状态,则对于为位移边界- 57 -条件所容许的任意虚位移,(5-14)式成立。反过来,如果(5-14)式对于为位移边界条件所容许的任意虚位移成立,则弹性体处于平衡状态。值得提出的是,不管材料的应力应变关系是线性还是非线性,虚功原理都成立。如果用下面泛函表示弹性体的总位能P∏,⎰⎰σ--ε=∏S ii V i i ij S u T V u F A d d ])([p (5-16) 对(5-16)式取驻值,即一阶变分等于零,⎰⎰σ=--εσ=∏S ii V i i ij ij S u T V u F 0d δd ]δδ[δP (5-17) 将(5-14)式与(5-17)式比较,显然,(5-17)式就是(5-14)式。所以,可以把总位能原理理解为虚功原理的另一种表达形式。由于⎰⎰⎰σ=+σ=εσV ji ij i j j i V ij V ij ij V u V u u V d δd )δδ(21d δ,,, (5-18) 利用格林公式,上式等号右边积分可变换为⎰⎰⎰σ-σ=σV ij ij S i j ij V j i ij V u S u n V u d δd δd δ,, 并引用(5-15b)式,则(5-17)式可化为0d δ)(d δ)(,=σ-++σ⎰⎰σS i j ij i V i i j ij S u n T V u F 因为i u δ为独立量,则由总位能驻值条件可导出:平衡方程(5-1)即0,=+σi j ij F (在V 内)及力的边界条件(5-5)即i j ij T n =σ(在σS 上)。(5-16)式表达了弹性体的最小位能原理:在满足应变位移关系(5-2)和位移边界条件(5-6)的所有容许的i u 中,实际的iu 使弹性体的总位能取最小- 58 -值。(二)余虚功原理与总余能原理余虚功原理中,可取ij σδ表示弹性体内的应力变分,即虚应力。另外,i T δ表示弹性体指定位移边界上的表面边界力的变分。与虚功方程相类似的余虚功方程可表示为0d δd δ=-σε⎰⎰u S ii V ij ij S u T V (5-19) 余虚功原理是在满足平衡方程(5-1)式及力的边界条件(5-5)式的条件下成立,即满足(5-1)式和(5-5)式的变分形式的条件为0δ,=σj ij (在V 内) (5-20) 0δ=i T (在σS 上) (5-21)现在定义下面的泛函为弹性体的总余能c∏⎰⎰-σ=∏u S ii V ij S u T V B d d )(c (5-22) 现在对(5-22)式取驻值,即0δc=∏,则有0d δd )(δδc =-σ=∏⎰⎰u S ii V ij S T u V B (5-23) 利用格林公式,上式中的体积分项可化为⎰⎰⎰⎰⎰σ-σ=σ=σε=σV j ij i S ij j i V ij j i ij V ij V ij V u S n u V u V V B d δd δd δd δd )(δ,,考虑到(5-21)式后,(5-23)式可写成0d δd δ)(,=σ-σ-⎰⎰V jij i S j ij i i V u S n u u u (5-24) 再考虑到ij σδ应满足(5-20)式,且ij σδ为独立量,则由c ∏的驻值条件可以导出位移边界uS 上的协调条件为0=-ii u u (5-25)(5-22)式表达了弹性体的最小余能原理:在满足平衡方程(5-1)和力的边界条件(5-5)的所有容许的应力σ中,实际的应力ijσ使弹性体的总余能ij取最小值。上面所讨论的变分原理,所提出的泛函是受一定条件约束的,如最小位能原理的泛函∏应满P足的条件是(5-2)式和(5-6)式,而最小余能原理的泛函∏应满足的条件是(5-1)式和(5-5)式。这种变c分原理称为不完全变分原理,或称为带约束条件的变分原理。§5.2 小位移弹性理论的完全及不完全广义变分原理§5.2.1 完全广义变分原理现在,让我们利用拉格朗日乘子法,导出小位移弹性理论的无条件的广义变分原理。在§5.1节的讨论中,不论是总位能原理或总余能原理,其能量泛函的提出是附带一定条件的即在满足一定条件下提出的。如果我们利用拉格朗日乘子法,将泛函提出的条件作为约束方程引入到泛函中去,则问题的性质就发生了变化,即将带有约束条件的泛函转化为不带任何约束条件的泛函。于是形成了下面的完全广义变分原理。(1) 基于总位能原理的小位移弹性理论的完全广义变分原理- 59 -- 60 -现在,让我们将总位能原理的初始满足条件即应变位移关系式(5-2)和位移边界条件(5-6),分别乘以定义在体积V 内的和位移边界u S 上的拉格朗日乘子ij λ和j μ,并与总位能泛函p ∏相加组成新的泛函Gp ∏,Gp ,,1[()]d [()]d 2ij i i ij ij i j j i V V A Fu V u u V ελε∏=-+-+-⎰⎰ ⎰⎰-μ+σu S i i i S i i S u u S u T d )(d(5-26)式中经受变分的独立量是ij ε,i u ,ij λ及iμ,而不需要附加任何条件。对这些独立量进行变分,有 ⎰⎰⎰⎰⎰⎰σ-μ-+μ+-+λ-λ+-ε+ελ+ε∂∂=∏S i i S i i i i i V i i V i j j i ij V ij i j j i ij V ij ij ij S u T S u u u V u F V u u V u u V A u d δd ]δ)(δ[d δd )δδ(21d δ)](21[d δ)(δ,,,,Gp引用(5-18)式及格林公式,上式第三个积分可化为 ⎰⎰⎰⎰λ-λ=λ=+λS V ij ij i j ij V j i ij V i j j i ij V u S u n V u V u u d δd δd δd )δδ(21,,,, 将上式代入Gpδ∏式中,得 ⎰⎰⎰σ+λ-μ-+λ-μ+-λ+λ+-ε+ελ+σ=∏S i i j ij S i i i i j ij i V i i j ij ij i j j i ij ij ij ij S u T n S u u u n V u F u u u d δ)(d ]δ)(δ)[(d ]}δ)(δ)(21[δ){(δ,,,Gp由0δGp =∏可以导出以下各式ij ij σ-=λ,)(21,,i j j i ij u u +=ε,0,=-λi j ij F (在V 内)(5-27a,b,c) j ij i n λμ=,ii u u = (在u S 上)(5-27d,e)- 61 - 0=+λi j ij T n (在σS 上) (5-27f)显然,(5-27c)式表示平衡方程,(5-27b)式表示应变与位移的关系式,将(5-27a)式代入(5-27d)式中,则得j ij i n σ-=μ,将(5-27a)式带入(5-27f)式得j ij n T σ=,表示力边界上的给定条件。从以上的推导中,清楚地看到完全广义变分原理可导出平衡关系(5-1)、应变位移关系(5-2)、力的边界上的给定表面力(5-5)式及位移边界上的指定位移(5-6)式。将乘子ij λ、j μ分别用ij σ-、j ij n σ-代替,则泛函Gp ∏可写成下列形式--σ+-ε-ε=∏⎰V ii ij i j j i ij ij V u F u u A }d )](21[)({,,Gp ⎰⎰-σ-σu S i i j ij S i i S u u n dS u T d )( (5-28)该式中经受变分的独立量是三类共15个,即ij ε、i u 和ij σ,而没有约束条件。于是,(5-28)式表示的完全广义变分原理可叙述为:满足(5-1)式~(5-6)式的解i u 、ij ε、ij σ,必使得泛函Gp ∏有驻值。(5-26)式和(5-28)式表示的广义原理,也称为胡海昌-鹫津原理。现在再讨论另一种形式的完全广义变分原理,即Hellinger-Reissner 变分原理,同属于无约束条件的广义变分。Hellinger-Reissner 泛函由下式定义,⎰⎰⎰μ-+--σ-σ=∏σuS iiiS ii Vii ijji ijS u u dS u T V u F B u d )(d ])([,R式中经受变分的独立量是ijσ、i u 和拉格朗日乘子iμ,而没有约束条件。对上式泛函取一阶变分,由驻值条件,可得--σσ∂σ∂-σ=∏⎰⎰⎰Vii VijijijVji ij V u F V B V u d δd δ)(d δδ,Rd δd δ)(d δ=μ+μ-+⎰⎰⎰σuuS i i S i i i S i i S u S u u S u T (5-29)上式等号右边第一个积分,可以进一步用分部积分展开,可得⎰⎰⎰⎰+-=VVijji iVjij Sijijji ijV u V u S u n V u d δd δd δd δ,,,σσσσ (5-30)将(5-30)式代回(5-29)式,经过整理后,可得下式+σ+-σ∂σ∂-+σ-=∏⎰⎰VijVij ji ijijiijij V u u B V u F d δ)](21)([d δ)(δ,,,R0d δμ)(d δ)μ(d δ)(=-+σ++-σ⎰⎰⎰σuuS iiiS S i j ij i i i j ij S u u S u n S u T n从上式中可以导出以下条件0=+σi ijF (在V 内) 平衡方程 0=-σijijT n (在σS 上) 力边界条件 0=-i i u u (在uS 上) 位移边界条件 并且可以得到拉格朗日乘子的涵意,jij i i n T σ-=-=μ如果引入关系式(5-12),即ijij ij B σσ∂=ε)(,则还可以得到)(21,,=+-εi j j i ij u u (在V 内) 应变位移关系从而验证了在泛函R∏极值条件下,导出了弹性力学各类基本方程。将乘子iμ用jijn σ-代替,泛函R∏可以写为下列形式--σ-σ=∏⎰Vii ij j i ij V u F B u d ])([,R⎰⎰σ--σuS jij i i S ii S n u u dS u T d )((5-31)式中经受变分的独立量共9个,即ij σ和iu ,而没有约束条件。从泛函R∏中不难看出,此种广义变分属于二类自变量的广义变分,ij σ和iu 是独立假设的。Hellinger-Reissener 泛函在构造弯曲板有限元模型得到广泛的应用(参阅本书第六章§6.3节)。实际上,将物理关系引入(5-28)式消去应变分量ijε,也可以得到(5-31)式。通过分部积分,泛函(5-31)也可以写成另一形式如下:-+σ+σ=∏-⎰Vii j ij ij V u F B d ])()([,*R⎰⎰σ--σσuS ij ij S ii j ij S u n dS u T n d )((5-31’)(2) 基于总余能原理的小位移弹性理论的完全广义变分原理现在我们从总余能泛函c∏出发,将弹性体内的平衡条件(5-1)及力的边界条件(5-5)分别用定义在V 内和σS 上的拉格朗日乘子i λ和iμ引入,并形成下面的泛函⎰⎰⎰σ-μ-σ+λ+σ+ε-εσ=∏σuS i j ij S i i j ij Vi i j ij ij ij ij Su n S T n V F A d d )(d ])()([,Gc式中ijσ、ijε、iλ和iμ均作为独立变量。对上式进行一阶变分,得+λ+σ+σλ-ε+εε-σ=∏⎰V F a ii j ij Vij j i ij ij kl ijkl ij d )δ(δ)(δ)[(δ,,Gc+σλ+μ+μ-σ⎰σS ijj i i i i j ij S n T n d ]δ)(δ)[(⎰σ-λuS ijj i i S n u d δ)((5-32)上式中d δ)(,=σλ-ε⎰Vijj i ij V ⎰σλ+λ-εViji j j i ij V d δ)](21[,, (5-33) 将(5-33)式代入(5-32)式,则由(5-32)式可以得到以下驻值条件:klijklija ε=σ,)(21,,i j j i ij u u +=ε,0,=+σij ij F (在V 内) (5-34a,b,c)jijin T σ=, iiλ-=μ (在σS上) (5-34d,e)ii u =λ(在uS 上) (5-34f)如果将上式得到的i μ和i λ代入Gc ∏式,则泛函Gc∏可以写为下列形式⎰⎰⎰σ--σ-+σ+ε-εσ=∏σuS ij ij S ii j ij Vii j ij ij ij ij S u n S u T n V u F A d d )(d ])()([,Gc(5-35)式中经受变分的独立量是三类共15个,即ij ε、iu 和ijσ,而没有约束条件。于是,(5-35)式表示的完全广义变分原理可叙述为:满足(5-1)式~(5-6)式的解iu 、ijε、ijσ,必使得泛函Gc∏有驻值。如果将平衡条件(5-1)及力的边界条件(5-5)分别用定义在V 内和σS 上的拉格朗日乘子i λ和iμ引入总余能泛函c∏,并形成下面的泛函⎰⎰⎰σμ-σ+σ-λ+σ+σ=∏S ii j ij S ij ij Vii j ij ij S T n S u n V F B ud )(d d ])()([,Gc1式中经受独立变分的量是ijσ、i λ和iμ。可以证明,上述的泛函与(5-31’)式的泛函是相同的,即-+σ+σ=∏⎰Vii j ij ij V u F B d ])()([,Gc1⎰⎰σ--σσuS ij ij S ii j ij S u n dS u T n d )((5-36)这是一个属于二类自变量的广义变分,其中的ijσ和iu 是独立假设的。实际上,将物理关系引入(5-35)式消去应变分量ijε,也可以得到(5-36)式。下面我们将进一步证明(5-28)式与(5-35)式的等在价性。将(5-28)式与(5-35)式相加,得到⎰⎰⎰σ-σ-σ+σ+=∏+∏σuS ij ij S ij ij Vij ij ij i j j i S u n S u n V u u u d d d ])(21[,,,GcGp 利用分部积分,⎰⎰⎰⎰σσ+σ=σ+σ=σ+σ+S S i j ij i j ij V i j ij ij j i V i j ij ij i j j i uSu n S u n Vu u V u u u d d d )(d ])(21[,,,,,从而得Gc Gp =∏+∏,或 GcGp∏-=∏ (5-37)(5-37)式证明了两种泛函的等价性。所以,完全变分原理的两种泛函即Gp∏与Gc∏是等价的,只是有正、负之差,但这对取驻值没有关系。从物理意义上也比较易于理解,由于小位移线性弹性系统的完全变分原理,在泛函中全部地概括了所有的条件,因此而构成其等价性。而对于一般总位能泛函p∏与总余能泛函c∏,这一等价性并不成立,读者可以自行验证。§5.2.2 有条件的不完全广义变分原理在§5.2.1节中,我们讨论了不附带任何条件的完全变分原理,对泛函取驻值,导出了所有的需要满足的条件。但实际情况也并非如此,譬如我们可以不要求完全变分原理的泛函,而只是在满足部分的条件(即放松提出泛函的某些条件的要求),再引用拉格朗日乘子法,组成不完全变分原理的泛函。不完全变分原理较多用于有限元素法中,如混合模型、基于位能原理的位移杂交模型或基于余能原理的应力杂交模型等。对于基于总位能原理的不完全广义变分原理列举几例,概述如下。(1)在满足位移边界条件(5-6)的所有允许变量ijσ、ijε、i u 中,只有当ij σ、ij ε、iu 为真实解时,使下面的泛函为驻值,d d }]λ)(21[)({,,mp1⎰⎰--+-+=∏σεεS ii Vii ij i j j i ij ij S u T V u F u u A (5-38) 式中ijσ、ijε、iu 均为独立变量。当对(5-38)式取驻值,有⎰-λ--ε+ελ+ε∂∂=∏Viji j j i ij ij ij iju u A δ)2121(δ)[(δ,,mp1⎰=-λuS i i i j i ij S u T V u F u 0d δ]d δ-δi , (5-39)利用格林公式,并引入ijijA σ=ε∂∂,可以得到⎰⎰⎰λ-λ=λVVij ij Sijijji ijV u S u n V u d δd δd δ,,将上式代入(5-39)式,同时注意到泛函是在满足位移边界(5-6)的条件下提出的,故上式等号右边第一项中的表面S 只包含力的边界,(5-39)式变为⎰+λ--ε+ελ+σ=∏Viji j j i ij ij ij ij u u δ)2121(δ)[(δ,,mp1⎰σ=+λ--λs i i j ij i i j ij S u T n V u F 0d δ)(d ]δ)(, (5-40)因为ijεδ、ijλδ、iu δ均为独立变量,由(5-40)式可导出 在体积V 内ijijσ-=λ,)(21,,i j j i ij u u +=ε,0,=+σij ij F (5-41a,b,c) 在力的边界σS 上jijin T λ-= (5-41d) 将(5-41a)式代入(5-41d)式中,得jijin T σ= (5-41d’) 将式(5-41a)式代入(5-38)式,则得泛函m p1∏为⎰⎰σ--σ+-ε-ε=∏S ii Vii ij i j j i ij ij S u T V u F u u A d d }])(21[)({,,mp1(5-38’) (2)在满足应变位移关系式(5-2)的所有容许的变量中,只有真实解使下面的泛函取驻值 ⎰-ε=∏Vii ijV u F A d ])([mp2⎰σ-S ii S u T d ⎰μ-+uS ii i S u u d )( (5-42)现在对m p2∏取驻值,即0δm p2=∏,有+--εε∂∂=∏⎰⎰σS i i Vi i ij ijS u T V u F Ad δd ]δδ[δmp20d ]δ)(δ[=μ-+μ⎰uS i i i i S u u u(5-43)引入(5-13)式,再利用格林公式,上式等号右边第一个积分中的第一项可化为⎰⎰⎰⎰-==Vi j ij S i j ij Vj i ij Vij ij Vu S u n V u V ud δd δd δd δ,,σσσεσ将上式代入(5-43)式,得+-σ++σ-=∏⎰⎰σS i i j ij Vi i j ij S u T n V u F d δ)(d δ)(δ,mp20d ]δ)(δ)[(=μ-+μ+σ⎰S u u u n uS iiii i j ij因为iu δ、iμδ为独立变量,故由上式可以导出以下条件,在体积V 内: 0,=+σijij F(5-44a)在力的边界σS 上: jij i n T σ=(5-44b)在位移u S 边界上: j ij i n σ-=μ,ii u u =(5-44c,d)现在将(5-44c)代入(5-42)式,可得泛函m p2∏为⎰-ε=∏Vii ij V u F A d ])([mp2⎰σ-S ii S u T d ⎰μ-+uS ii i S u u d )( (5-42’)(3)设位移边界条件为)3,2,1(==i u u ii。在满足其中一个位移边界条件如11u u =的所有容许的i u 、ij ε、ijσ中,只有当i u 、ij ε、ijσ为真实解时,使下面的泛函有驻值⎰--σ+-ε-ε=∏V i i ij i j j i ij ij V u F u u A d })](21[)({,,mp3⎰σS i i S u T d ⎰σ-+σ--uS jjj j S n u u n u u d ])()[(333222 (5-45)这种不完全满足位移边界的泛函,可以只满足其中一部分位移边界条件,如式(5-45)那样,也可以满足其中的两个位移边界条件,而形成相应的泛函。具体推导读者可自行完成。(4)在满足一个应变位移关系01,111=-εu 的所有容许的位移i u 、应变ij ε及应力ij σ中,真实的i u 、ij ε、ijσ必使下列泛函为驻值--σ-ε+σ+-ε-ε=∏⎰Vii ij i j j i ij ij V u F u u u A d })()](21[)({111,111,,mp4⎰⎰σσ--S S jij i i ii uS n u u S u T d )(d(5-46)基于总余能原理的不完全广义变分原理,其基本处理方法与上面类似,仍是利用拉格朗日乘子法,使一部分条件乘以拉格朗日乘子作为泛函的一部分,参与到泛函中去,而将另一部分条件作为泛函提出的条件。按泛函提出满足不同的条件,也可以划分为以下几种。(1/)在满足力的边界条件(5-5)的所有容许的位移i u 、应变ij ε及应力ij σ中,只有真实的i u 、ij ε、ijσ使下面的泛函有驻值⎰⎰σ-λ+σ+ε-σε=∏uS ij ij Vii j ij ij ij ij S u n V F A d d ])()([,mc1(5-47)式中ij σ,ij ε和拉格朗日乘子iλ均作为独立变量。在引用了(5-13)式和(5-3)式,即ijkl ijkl ij ijijij a A A εε=εε∂ε∂=εδδ)()(δ 及格林公式,使⎰⎰⎰σλ-σλ=σλVij j i Sij j i Vj ij i VS n V d δd δd δ,,后,对(5-47)式取驻值,可得到下式⎰⎰=σ-λ-λ+σ+σλ-ε+εε-σ=∏uS ij j i i Vi i j ij ij j i ij ij kl ijkl ij S n u V F a 0d δ)(d ]δ)(δ)(δ)[(δ,,mc1因为ijεδ、λδ、ijσδ都是独立变量,故由上式可导出以下驻值条件,在体积V 内:kLijkLija ε=σ, 0,=+σij ij F (5-48a,b) 由⎰⎰=σλ-=σλ-εVVijj i i ijj i ij V u V 0d δ)(d δ)(,,可知,在体积V 内,iiu λ= (5-48c) 而在位移边界uS 上,ii u =λ (5-48d) 将(5-48c)及(5-48d)代入(5-47)式中,得⎰⎰σ-+σ+ε-σε=∏uS ij ij Vii j ij ij ij ij S u n V u F A d d ])()([,mc1(5-47’)(2/)在满足平衡方程式(5-1)的所有容许的iu 、ijε、ijσ中,只有当i u 、ij ε、ijσ为真实解时,使下面泛函有驻值⎰⎰⎰σ-μ-σ+ε-σε=∏σuS ij ij S ii j ij Vijij ij S u n S T n V A d d )(d )]([mc2(5-49)式中应力ijσ,应变ijε,乘子iμ是作为独立变量。对泛函(5-49)取驻值,⎰⎰⎰=σ-+δσ+μ+μ-σ+σ-εε-σ=∏σuS ij j i i S ij j i i i i j ij Vj ij i ij kl ijkl ij S n u u S n u T n V u a 0d δ)(d ])(δ)[(d ]δδ)[(δ,mc2推导上式,我们用了格林公式,使⎰⎰⎰⎰σ-σ=σ=σεVj ij i Vij j i Vij j i Vij ij Vu S n u V u V d δd δd δd δ,,由此可导出以下各式0,=ε-σklijkljij a (在V 内) j ij i n T σ=,i i u -=μ (在σS 上)i i u u = (在uS 上) (5-50a,b,c,d)现在将(5-50c)式代入(5-49)式中,可得出泛函mc2∏为 ⎰⎰⎰σ--σ-ε-σε=∏σuS ij ij S ii j ij Vijij ij S u n S u T n V A d d )(d )]([mc2(5-49’)(3/)在满足一个(譬如全部共有三个)给定力边界条件如jjn T 11σ=的所有容许的iu 、ijε、ijσ中,只有真实的i u 、ij ε、ijσ使下列泛函为驻值-σ-+σ+ε-σε=∏⎰⎰uS ij ij Vii j ij ij ij ij S u n V u F A d d ])()([,mc3⎰σ-σ+-σS j j j j S u T n u T n d ])()[(333222 (5-51)同样,如果要求的泛函满足二个以上给定力边界条件时,可以参考(5-51)式,也不难求出其泛函表达式。读者可以自行推导。§5.3 小位移弹性理论的分区变分原理传统变分原理采用整体插值,而有限元素法是把整体分割为有限个元素的集合体,采用的是分区插值。将分区概念引入变分原理,用分区插值代替整体插值,并且放松各个分区交界面上的连续性要求,就得到所谓的分区变分原理。分区变分原理是变分原理与分区概念相结合的产物,为建立新型的有限元模型提供了坚实的理论基础。设一个连续的弹性体被划分为若干个分区或单元(如图5-1所示),其体积分别为),,3,2,1(N e V e=。任一分区e 的体积力为e iF ,表面为e S ,eS 一般由三部分组成:*e e eue e S S S S 'σ∑++=其中,ue S 为e S 中包含给定位移iu 的边界面,e S σ为eS 中包含给定表面力iT 的边界面,*e e S '为eS 与相邻分区e '的交接面。在分区变分原理中,各个分区按需要可任意定为位能区(如图5-1中的分区(p1V ,p2V , p3V )或余能区(如图5-1中的分区c3c2c1,,V V V )。各个分区中独立变分的量可以任意定为三类变量(位移i u ,应力ij σ,应变ijε)或两类变量(i u 和ij σ)或一类变量(i u 或ijσ)。相邻分区的交接面分为pp S 、cc S 、pc S 三类,pp S 表示其两侧都是位能区,ccS 的两侧都是余能区,pcS 的一侧是位能区,另一侧是余能区。各个分区的各类变量不仅可以独立变分,而且在边界面上可以要求或不要求满足给定的位移或面力边界条件,在分区的交接面上也可以要求或不要求满足交接面上位移或面力的连接条件(即位移相容条件和力平衡条件)。小位移弹性理论的分区变分原理的泛函一般可写成下面形式图5-1 分区示意图∑∑∑∑∑---∏-∏=∏pcccppcppccc pp c p S S S V V H H H (5-52)上式等式右边各项的涵义为,第一项为各位能区pV 的总位能p∏或广义的总位能Gp∏之和,第二项为各余能区c V 的总余能c ∏或广义的总余能Gc∏之和,第三、四、五项分别表示相邻分区交接面处的附加能量之和,取决于交接面的类型。根据分区的性质,我们可以把分区变分原理归结为以下三类,(1)位能分区变分原理。弹性体在整体上被分割成有限个位能区的集合体,并基于最小位能原理导出的修正变分原理。(2)余能分区变分原理,弹性体在整体上被分割成有限个余能区的集合体,并基于最小余能原理导出的修正变分原理。(3)混合分区变分原理,弹性体在整体上被分割成有限个位能区和余能区的集合体,是上述两类修正变分原理的混合。分区变分原理是基于传统变分原理的一种修正变分原理,与§5.2节的完全与不完全变分原理不同的是,后者可以看作是在单元水平上进行修正与混合,而分区变分原理则是在弹性体整体水平上进行修正与混合。下面我们将在传统变分原理的基础上,为有限元素的集合体进行分区变分原理的公式推导。§5.3.1 位能分区变分原理为了以后方便,现在用aV 和b V 表示两个任意的相邻元素,用abS 表示a V 和bV 的交接面,如图5-2所示。另外引用两个符号}{*aab abV S S ∂∈=和}{*bab baV S S ∂∈=来区别交接面属于a V 的还是属于b V 的(这里a V ∂表示aV 的整个边界)。(1)修正最小位能原理设每个元素的广义位移表示为)1(i u ,)2(i u ,…,)(a i u ,)(b i u ,…,)(N iu ; 3,2,1=i如果选择的每一个元素的位移函数满足下列要求:(ⅰ)在元素内,是连续的和单值的;(ⅱ)在元素的交接面上,满足位移相容条件,即在abS 上,)()(b ia i u u = (5-53) (ⅲ)如若元素的边界包含有uS ,则该元素的位移函数应满足位移边界条件(5-6)。则这些位移函数的集合可以作为最小位能原理泛函的容许位移函数,那么,元素集合体的最小位能原理的泛函就由下式给出∑⎰⎰∑--=∏=∏}d ]d )([{pImp aaS ii V ii i S u T V u F u A σ (5-54)式中经受变分的独立量是)(a iu ,p∏是由(5-16)式确定图5-2 a V 、b V 、abS的元素aV 的总位能泛函。 (2)修正位能原理如果我们放松元素交接面上的位移相容条件(5-53)式,将约束条件(5-53)利用定义在abS 上的拉格朗日乘子iλ引入到(5-54)式的泛函表达式中,则形成下面的泛函:∑⎰∑--∏=∏abS ib ia i S u u d λ)()()(pImp1 (5-55)式中的)(a iu 和iλ是经受变分的独立变量,并带有约束条件(5-6)。对(5-55)式取驻值,+-++-=∏⎰∑⎰}d δ)(d δ)({δ,Imp1aaS i i j ij V i i j ij S u T n V u F σσσ∑⎰⎰-++-**d δ)λ(d δ)λ({)()()()()()(baabS b iib jb ij S a iia ja ijS u n S u n σσ⎰=-abS ib ia i S u u 0}d δλ)()()(由以上的驻值条件,可导出下列的关系式,0,=+σi j ij F (在aV 内)(5-56a)j ij i n T σ= (在aS σ上)(5-56b))()(a j a ij in σ=λ(在*abS 上),)()(λb j b ij in σ-=(在*baS 上) (5-56c) 0)()(=-b ia i u u (abS 上)(5-56d)式中)(a i n 与)(b i n 分别表示沿*ab S 与*baS 上外法线方向的方向余弦,对同一点来说,有)()(b j a j n n -=显然,(5-56a)为平衡方程(5-1)式,(5-56b)为力的边界(5-5)式,(5-56c)为乘子iλ,(5-56d)为位移相容条件。令)(a iT 和)(b iT 分别等于)()(a j a ij n σ及)()(b jb ij n σ,即有)()()(a ja ij a in T σ= , )()()(b jb ij b in T σ= (5-57) (5-57)式指明了拉格朗日乘子i λ的物理意义,即iλ就等于ab S 上的表面力)(a i T (注意)(a iT 是)(a iu 的函数,和记作)()()()(a ia ia i u T T =)。将)(a ii T =λ代入(5-55)式,得到 ∑∑-∏=∏1pp p Imp1H(5-58)而⎰-=abS b ia i a iS u u T H d )()()()(1pp 或⎰-abS a ib i b iS u u T d )()()()( (5-59)(5-58)式给出的原理称为放松连续性要求的第一修正位能原理,因为在1Im p ∏中放松了(5-53)式的要求,每一个元素的位移函数可以独立选择而不用考虑元素交接面上的位移相容条件的要求。这里要指出的是,这个修正原理不再是最小原理了,而仅仅保持其驻值性质。泛函1Im p ∏还可以作进一步的处理。若我们引进两个函数)(a iλ与)(b iλ,它们分别定义在*abS 与*baS 上,且服从下列关系式:0)()(=λ+λb ia i(A)由(A)式的条件,可见:)(a iiλ=λ , )(b iiλ=λ- (B) 现在将(B)式代入(5-55)式中,等号右边末项积分的被积函数就变为以下形式)()()()(b ib ia ia iu u λ+λ (C)并附带约束条件(A)。因此,可以引入一个定义在abS 上新的拉格朗日乘子iμ将约束条件(A)加入到泛函(5-55)中,于是(5-55)式可改写为下面等价形式: ∑∑-∏=∏2pp p 2Imp H (5-60) 而⎰+-+=abS b ia i ib ib i a i a i S u u H d )]λλ(μλλ[)()()()()()(2pp⎰⎰-+-=**d )μ(λd )μ(λ)()()()(baabS ib ib i S ia ia i S u S u (D)(5-60)式称为放松连续性要求的第二修正位能原理,式中经受变分的独立量是)(a iu 、)(a iλ和iμ,带有约束条件(5-6)式。其中,在元素aV 中的)(a i u 及在*ab S 上的)(a iλ与在元素bV 中的)(b i u 及在*ba S 上的)(b iλ都可以独立选取,但必须在元素交接面ab S 上有共同的iμ,以保证交接面处位移的协调性。取(5-60)式的驻值,可得 +-+--=∏⎰∑⎰}d δ)(d ]δ)[({δ,2Imp aaS ii j ij V ii j ij S u T n V u F σσσ∑⎰⎰--+-**d δ)λ(d δ)λ({)()()()()()(baabS b ib i b iS a ia i a iS u T S u T +---⎰⎰**d δλ)μ(d δλ)μ()()()()(baabS b iib iS a iia iS u S u}d δμ)λλ()()(⎰+abS ib ia i S(E)由此得到在abS 上的下列驻值条件:)()(a ia iT =λ,)()(b ib iT =λ (5-61a,b) )(a iiu =μ, )(b iiu =μ (5-61c,d) 及0)()(=λ+λb i a i(5-61e)(5-61)式的物理意义十分明显。将(5-61a,b)代入(5-61e),得0)()(=+b ia iT T (5-61f) (5-61f)表示在交接面abS 上,力是平衡的。如果将驻值条件(5-61a,b)引入2ab H 中消去)(a iλ和)(b iλ,就可以把2pp H 改写成另一形式如下⎰⎰-+-=**d )μ(d )μ()()()()(3pp baabS ib ib iS ia ia iS u T S u T H (F)并得到∑∑-∏=∏3pp p Imp3H (5-62)这个原理称为放松连续性要求的第三修正位能原理,式中经受变分的独立量是)(a iu 和iμ,带有约束条件(5-6)式。在这些变分的量中,aV 内的)(a iu 与bV 内的)(b iu 都可以独立选择,但是iμ对于*ab S 和*baS 必须是共同的。(3)修正广义位能原理下面我们将从Im p2∏出发,导出一种修正广义变分原理。即满足平衡方程(5-1)、应变位移关系式(5-2)、物理关系式(5-3)、位移边界条件(5-5)及力的边界条件(5-6)及在元素交接面上满足位移协调条件和力平衡条件的解,使下列泛函有驻值:-+-εσ--ε=∏∑⎰aV ji ji ijijii ijV u u u F A d )]}(21[)({{,,ImGp1∑⎰⎰--σ-σ2pp }d )(d H S u u n S u T uaaS i i j ij S i i (5-63)式中经受变分的独立量是)(a ijε、)(a ijσ、)(a iu 、)(a iλ和iμ,而不带约束条件。可以证明,在abS 上,m Gp1∏的驻值条件也给出(5-61a,b,c,d,e)式表示的方程。因此,我们可以把ImGp1∏写成另一等价形式如下:-+-εσ--ε=∏∑⎰aV ji j i ij ij i i ij V u u u F A d )]}(21[)({{,,ImGp2∑⎰⎰--σ-σ4pp }d )(d H S u u n S u T uaaS i i j ij S i i (5-64) 式中⎰⎰-+-=**d )μ(d )μ()()()()(4pp baabS i b i b i S i a i a i Su T S u T H (G)(5-64)式中经受变分的独立量是)(a ijε、)(a ijσ、)(a iu 和iμ,而不带约束条件。(4)修正Hellinger-Reissner 原理利用应变位移关系式(5-2),从泛函ImGp2∏中消去应变分量ijε就导致修正Hellinger- Reissner 泛函: --σ---σ-σ=∏⎰⎰∑⎰σ}d )(d ])([{,ImRuaaaS ii j ij S ii V ii ij j i ij S u u n dS u T V u F B u ∑⎰+-+abS b ia i ib ib ia ia iS T T u T u T d )](μ[)()()()()()((5-65)式中经受变分的独立量是)(a ij σ、)(a iu 和iμ,而不带约束条件。利用分部积分,可以得到修正Hellinger-Reissner 泛函的另一表达式如下:--σ-σ+σ=∏-⎰∑⎰σaaS iijijV iijij ijdS u T n V u F B )(d ])()([{,*ImR∑⎰⎰+-abuaS ib ia iS ij ijS T T S u n d μ)(}d )()(σ (5-66)式中经受变分的独立量是)(a ijσ、)(a iu 和iμ,没有约束条件。§5.3.2 余能分区变分原理我们也可以从最小余能原理出发,导出有限元集合体的最小余能原理、修正余能原理以及修正广义变分原理等。用下列记号来表示每个元素中的应力:)1(ijσ,)2(ijσ,…,)(a ijσ,)(b ijσ,…,)(N ijσ; 3,2,1=j i ,如果选择的每一个元素的应力函数满足下列要求:(ⅰ)在元素中,是连续的和单值的,并且满足平衡方程(5-1);(ⅱ)在元素的交接面上,满足平衡条件,即 在ab S 上, 0)()(=+b ia i T T (5-67) 式中)(a i T 和)(b iT 是由(5-57)式定义的;(ⅲ)如若元素的边界包含有σS ,则该元素的应力函数应满足力边界条件(5-5)。这些满足上述条件的应力函数的集合可以作为最小余能原理泛函的容许函数,那么,元素集合体的最小余能原理的泛函就可以由下式给出。


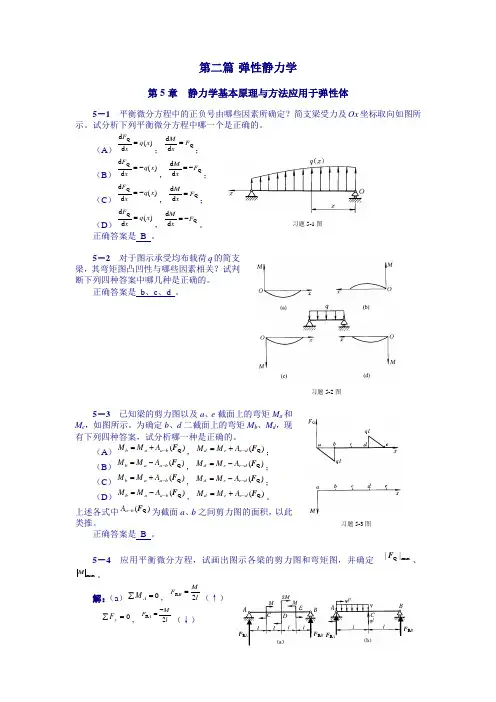
习题5-1图习题5-2图习题5-3图第二篇 弹性静力学第5章 静力学基本原理与方法应用于弹性体5-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Qx q xF =;Q d d F x M=;(B ))(d d Qx q xF -=,Qd d F x M-=; (C ))(d d Qx q xF -=,Qd d F x M=;(D ))(d d Qx q xF =,Qd d F x M-=。
正确答案是 B 。
5-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
正确答案是 b 、c 、d 。
5-3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ,如图所示。
为确定b 、d 二截面上的弯矩M b 、M d ,现有下列四种答案,试分析哪一种是正确的。
(A ))(Q F b a a b A M M -+=,)(Q F d e e d A M M -+=; (B ))(Q F b a a b A M M --=,)(Q F d e e d A M M --=; (C ))(Q F b a a b A M M -+=,)(Q F d e e d A M M --=; (D ))(Q F b a a b A M M --=,)(Q F d e e d A M M -+=。
上述各式中)(Q F b a A -为截面a 、b 之间剪力图的面积,以此类推。
正确答案是 B 。
5-4 应用平衡微分方程,试画出图示各梁的剪力图和弯矩图,并确定 m a x Q ||F 、maxM。
解:(a )0=∑A M ,l MF B 2R =(↑)0=∑y F ,lM F A2R -=(↓)F R AF R BF R BABABCDCEF R AF R B F R Al MF 2||m a x Q =, M M 2||max =(b )0=∑A M022R 2=⋅+⋅+⋅--l F l ql lql ql BqlF B41R =(↑)=∑y F ,ql F A 41R -=(↓)2R 4141ql l ql l F M B C =⋅=⋅=(+)2ql M A =ql F 45||max Q =, 2max ||ql M =(c )0=∑y F ,ql F A =R (↑)0=∑A M ,2ql M A =0=∑D M ,022=-⋅-⋅+D M lql l ql ql223ql M D=ql F =max Q ||, 2max 23||qlM =(d )0=∑B M 0232R =⋅-⋅⋅-⋅l ql ll q l F Aq lF A 45R =(↑)0=∑y F ,qlF B 43R =(↑)0=∑B M ,22l q M B= 0=∑D M ,23225ql M D=ql F 45||max Q =, 2max 3225||ql M =(e )0=∑y F ,F R C = 0 0=∑C M ,0223=+⋅+⋅-C M lql l ql2ql M C =0=∑B M ,221ql M B ==∑y F ,ql F B =Qql F =max Q ||, 2max ||ql M =M ACF R ABABACF R BF R AF R CBAF R AF R CM CCABC习题5-6图(f)0=∑AM,qlF C21R=(↑)=∑y F,qlF A21R-=(↓)=∑y F,021Q=-+-BFqlqlqlF B21Q==∑DM,042221=+⋅-⋅DMllqlql,8D, 8EqlF21||maxQ=,2max81||qlM=5-5其剪力图如图所示。

工程力学中的弹性力学分析弹性力学是工程力学中的一个重要分支,研究物体在外力作用下的变形和应力分布规律。
它的应用广泛,涉及到许多领域,如结构设计、材料科学等。
本文将介绍弹性力学的基本概念、应力和应变的关系以及一些常见的弹性力学分析方法。
一、弹性力学的基本概念1.1 响应函数在弹性力学中,响应函数描述了物体对外力的响应。
它是外力和物体的变形之间的关系,通常用应力-应变关系表示。
响应函数的形式根据物体的几何形状和材料的性质而定。
1.2 弹性力学模型弹性力学模型用于描述物体的变形行为。
常见的模型有胡克定律、泊松比等。
胡克定律指出应力和应变成正比,泊松比描述了材料在受拉伸或压缩时横向收缩或扩张的程度。
1.3 应力集中与材料破坏应力集中是指物体中某一点受到的应力远大于其周围区域的应力。
当应力集中超过了材料的极限强度时,材料可能发生破坏。
弹性力学分析常考虑应力集中和材料的极限强度,以保证结构的安全性。
二、应力和应变的关系应力和应变是弹性力学中的核心概念,用于描述物体受力后的变形行为。
应力是单位面积上的力,可以分为正应力、剪应力等。
应变是物体长度或体积相对变化的度量,可以分为线性应变、剪应变等。
三、常见的弹性力学分析方法3.1 静力学方法静力学方法是最基本的弹性力学分析方法之一,根据力平衡定律和物体的几何特征来求解应力和位移。
通常适用于简单的静力学问题,如梁的弯曲和轴的伸缩。
3.2 弹性势能法弹性势能法是一种能量方法,将物体的变形看作是内能的变化。
通过最小化弹性势能的原理,可以得到物体的平衡位置和应力分布。
这种方法适用于复杂的弹性力学问题,如结构的稳定性分析。
3.3 有限元方法有限元方法是一种数值分析方法,将实际物体离散为有限数量的单元,通过求解单元边界的约束条件来获得整个物体的应力和位移分布。
这种方法适用于复杂的几何形状和材料非均匀性的问题。
四、弹性力学在工程中的应用弹性力学在工程领域有广泛的应用。
例如,在结构设计中,弹性力学分析用于确定结构的强度和稳定性。
