第三章 无限长单位脉冲响应1
- 格式:ppt
- 大小:1.75 MB
- 文档页数:51



3-1设系统的微分方程式如下:(1)0.2c(t) 2r(t)单位脉冲响应:C(s) 10/s g(t) 103t3 3tc(t) 1 e cos4t e si n4t413-2 温度计的传递函数为 —,用其测量容器内的水温,1min 才能显示出该温度的Ts 198%的数值。
若加热容器使水温按 10(C/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数由一阶系统阶跃响应特性可知: c(4T) 98 o o ,因此有 4T 1 min ,得出T 0.25 min 。
视温度计为单位反馈系统,则开环传递函数为(s)1K 1TG(s)—1(s) Tsv 1用静态误差系数法,当r(t) 10t 时,e ss10 10T 2.5 C oK(2) 0.04c(t)0.24c(t) c(t)r(t)试求系统闭环传递函数① 部初始条件为零。
解:(s),以及系统的单位脉冲响应 g(t)和单位阶跃响应 c(t)。
已知全(1)因为 0.2sC(s)2R(s) 闭环传递函数(s)C(s) 10R(s) s单位阶跃响应c(t) C(s) 10/s 2c(t) 10t t 0(2) (0.04s 20.24s 1)C(s) R(s)C (s )闭环传递函数(s)C(s) R(s)120.04s0.24s 1单位脉冲响应:C(s)120.04s 2 0.24s 1g(t)25 e 33tsi n4t单位阶跃响应h(t) C(s)25 s[(s 3)216]1 s 6 s (s 3)216(s)1 Ts 1解法二依题意,系统误差疋义为e(t) r(t) c(t),应有e(s)E(s)1 C(s)R(s)11 TsR(s) Ts 1 Ts 13-3 已知二阶系统的单位阶跃响应为c(t) 10 12.5e 1.2t sin(1.6t 53.1o)试求系统的超调量c%、峰值时间t p和调节时间t'si n( 1n t )t p Jl- 1.96(s■1 2n1.63.5 3.5t s 2.92(s)n 1.2或:先根据c(t)求出系统传函,再得到特征参数,带入公式求解指标。

3-1 设系统的微分方程式如下:(1) )(2)(2.0t r t c= (2) )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C `闭环传递函数124.004.01)()()(2++==s s s R s C s φ单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s C t e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK !用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
解法二 依题意,系统误差定义为 )()()(t c t r t e -=,应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T sTs Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 203-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ%、峰值时间tp 和调节时间ts 。



1、 信号常分为 模拟信号 , 连续时间信号 , 离散时间信号 , 数字信号 。
2、 模拟信号是 时间 连续,幅度也 连续 的信号。
3、 连续时间信号是在规定的 连续 时间内,信号的 幅度 可以连续的,也可以是 离散的信号。
4、 离散时间信号是在一组 离散 的时间下,表示信号 数值 的函数。
5、 数字信号是在 时间 上和 幅度 上都经过 量化 的信号。
6、 系统是指反应信号处理 因果关系的设备或运算 。
7、 系统可分为 连续时间系统 , 离散时间系统 , 模拟系统 , 数字系统 。
8、 连续时间系统是指输入输出皆为 连续时间信号 的系统。
9、 离散时间系统是指输入输出皆为 离散时间信号 的系统。
10、模拟系统是指输入输出皆为 模拟信号 的系统。
11、数字系统是指输入输出皆为 数字信号 的系统。
12、处理就是 变换 ,数字信号处理就是用 数字 的方法,对信号的波形进行变换。
13、数字信号处理是 多种计算机算法的 汇集,因此可以认为它是 计算数学 的另一个分支。
14、数字信号处理的主要内容是 数字滤波 , 谱分析 。
15、数字信号处理的主要理论为 离散时间线性非时变系统 , 离散傅里叶变换 。
16、数字信号处理的过程可分为 前置取样 , A/D , 数字信号处理 , D/A 。
17、数字信号处理突出的优点 精度高 , 灵活性大 , 可靠性强 , 易于大规模集成,时分复用 。
1、信号的取样可分为 实际取样 , 理想取样 。
2、 理想 取样可以看出是实际取样的 科学的本质 的抽象。
3、著名的山农取样定理是h s Ω≥Ω2。
4、折叠频率=0Ω2/s Ω。
5、奈奎斯特频率=h Ω 信号中最高频率 。
6、奈奎斯特取样频率为h Ω2。
7、离散时间信号是用 序列 表示8、序列的运算规则有 积 , 加减 , 标乘 , 延时 , 分支运算 。
9、常用典型序列 单位取样序列 , 单位阶跃序列 , 矩形序列 , 正弦序列 ,实指数序列 , 复指数序列 。


第三章系统的时间响应分析机械⼯程控制基础教案Chp.3时间响应分析基本要求(1) 了解系统时间响应的组成;初步掌握系统特征根的实部和虚部对系统⾃由响应项的影响情况,掌握系统稳定性与特征根实部之间的关系。
(2 ) 了解控制系统时间响应分析中的常⽤的典型输⼊信号及其特点。
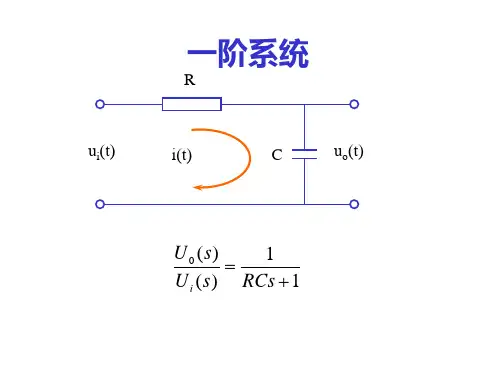
(3) 掌握⼀阶系统的定义和基本参数,能够求解⼀阶系统的单位脉冲响应、单位阶跃响应及单位斜坡响应;掌握⼀阶系统时间响应曲线的基本形状及意义。
掌握线性系统中,存在微分关系的输⼊,其输出也存在微分关系的基本结论。
(4) 掌握⼆阶系统的定义和基本参数;掌握⼆阶系统单位脉冲响应曲线、单位阶跃响应曲线的基本形状及其振荡情况与系统阻尼⽐之间的对应关系;掌握⼆阶系统性能指标的定义及其与系统特征参数之间的关系。
(5) 了解主导极点的定义及作⽤;(6) 掌握系统误差的定义,掌握系统误差与系统偏差的关系,掌握误差及稳态误差的求法;能够分析系统的输⼊、系统的结构和参数以及⼲扰对系统偏差的影响。
(7) 了解单位脉冲响应函数与系统传递函数之间的关系。
重点与难点重点(1) 系统稳定性与特征根实部的关系。
(2) ⼀阶系统的定义和基本参数,⼀阶系统的单位脉冲响应、单位阶跃响应及单位斜坡响应曲线的基本形状及意义。
(3) ⼆阶系统的定义和基本参数;⼆阶系统单位脉冲响应曲线、单位阶跃响应曲线的基本形状及其振荡情况与系统阻尼⽐之间的对应关系;⼆阶系统性能指标的定义及其与系统特征参数之间的关系。
(4) 系统误差的定义,系统误差与系统偏差的关系,误差及稳态误差的求法;系统的输⼊、系统的结构和参数以及⼲扰对系统偏差的影响。
难点(1) ⼆阶系统单位脉冲响应曲线、单位阶跃响应曲线的基本形状及其振荡情况与系统阻尼⽐之间的对应关系;⼆阶系统性能指标的定义及其与系统特征参数之间的关系。
(2) 系统的输⼊、系统的结构和参数以及⼲扰对系统偏差的影响。
建⽴数学模型后进⼀步分析、计算和研究控制系统所具有的各种性能。

3-1 设系统的微分方程式如下:(1) )(2)(2.0t r t c =&(2) )()()(24.0)(04.0t r t c t c t c =++&&&试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC = 闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
第一章习题一. 判断题1. 周期分别为N1,N2的两离散序列,在进行周期卷积后,其结果也是周期序列。
对2. FFT可用来计算IIR滤波器,以减少运算量。
错3. 相同的Z变换表达式一定对应相同的时间序列。
正确答案是: 错4. 频率采样法设计FIR滤波器,增加过渡带采样点可增加过渡带衰减。
正确答案是: 对二、选择题1. 采样率过低时,______。
A 量化误差增加 b. 必须增加信号频率c. 产生混叠2. 滤波器的单位脉冲响应的DTFT给出了滤波器的_____。
a. 频率响应b. 幅度c. 相位3. 滤波器的单位脉冲响应的DTFT给出了滤波器的_____。
a. 频率响应b. 幅度c. 相位4. ____序列的收敛域在Z平面上是一环状的。
a. 右边序列b. 双边序列c. 有限长序列5. 稳定系统的收敛域应当_______。
a. 包含单位圆b. 不包含单位圆c. 可以包含单位圆6. A/D 是_____的缩写a. asynchronous digitalb. analog to digitac. analog to discrete7. 连续信号的理想采样值是_____。
a. 连续的b. 离散的c. 时间上连续的8. 一个离散系统,a. 若因果必稳定b. 若稳定必因果c. 稳定与因果无关9. 下列哪一个不是信号的实例a. 语音b. 音乐c. 调制解调器10. 若输出不超前于输入,该系统称为______。
a. 线性b. 非线性c. 因果11. 抗混叠滤波器的目的是a. 去掉模拟信号混叠b. 等效一个高通滤波器c. 将高于采样率一半的频率分量去掉12. 抽样可以表述为______。
a. 将数字信号转化为模拟信号b. 将模拟信号转化为数字信号c. 获得模拟信号的幅度值13. 下面哪个表达式是将x(n)左移三位得到_______a. 3x(n)b. x(3n)c. x(n+3)14. 下面哪个表达式是将x(n)右移三位得到_______a. 3x(n)b. x(3+n)c. x(n-3)15. 关于线性系统的描述正确的是_____a. 遵从叠加原理b. 非时变c. 因果16. D/A变换的第一步是a. 零阶保持 b . 低通抗混叠滤波 c. 将数字代码转换为相应的模拟电平级三、计算题1. 和表示一个序列及其傅氏变换,并且为实因果序列,利用求下列各序列的傅氏变换:解:注意:当t为偶数时[ .] =2x(2n),当t为奇数时[ .] =0分析:以频率为400Hz的正弦信号为例,分别以2000Hz和1000Hz进行采样,序列长分别为2048点和1024点,对应的频谱如图1、图2所示。
3-1 设系统特征方程式:4322101000s s Ts s ++++=试按稳定要求确定T 的取值范围。
解:利用劳斯稳定判据来判断系统的稳定性,列出劳斯列表如下:4321011002105100(10250)/(5)100s T s s T s T T s ---欲使系统稳定,须有5025102500T T T ->⎧⇒>⎨->⎩ 故当T>25时,系统是稳定的。
3-2 已知单位负反馈控制系统的开环传递函数如下,试分别求出当输入信号为,21(),t t t 和 时,系统的稳态误差(),()().ssp ssv ssa e e e ∞∞∞和22107(1)8(0.51)(1)()(2)()(3)()(0.11)(0.51)(4)(22)(0.11)s s D s D s D s s s s s s s s s ++===++++++解:(1)根据系统的开环传递函数可知系统的特征方程为: ()(0.11)(0.51)100.050.6110D s sz s s s =+++=++=由赫尔维茨判据可知,n=2且各项系数为正,因此系统是稳定的。
由G(s)可知,系统是0型系统,且K=10,故系统在21(),t t t 和输入信号作用下的稳态误差分别为: 11(),(),()111ssp ssv ssa e e e K ∞==∞=∞∞=∞+ (2)根据系统的开环传递函数可知系统的特征方程为: 432()6101570D s s s s s =++++=由赫尔维茨判据可知,n=2且各项系数为正,且2212032143450,/16.8a a a a a a a ∆=-=>∆>=以及,因此系统是稳定的。
227(1)(7/8)(1)()(4)(22)s(0.25s+4)(0.5s 1)s s D s s s s s s ++==+++++由G(s)可知,系统式I 型系统,且K=7/8,故系统在21(),t t t 和 信号作用下的稳态误差分别为:()0,()1/,()ssp ssv ssa e e K e ∞=∞=∞=∞ (3)根据系统的开环传递函数可知系统的特征方程为: 32()0.1480D s s s s =+++=由赫尔维茨判据可知,n=2且各项系数为正,且21203 3.20a a a a ∆=-=>因此系统是稳定的。