2018-2019八年级数学上册 第12章 全等三角形课后作业题十五(无答案)(新版)新人教版

第12章《全等三角形》同步练习（§12.1～12.2）班级 学号 姓名 得分一、填空题（每题3分，共30分）1．如图，△ABC ≌△DEF ，A 与D ，B 与E 分别是对应顶点，∠B =32o ，∠A =68o ，AB =13cm ，则∠F =______度，DE =______cm ．2．由同一张底片冲洗出来的两张五寸照片的图案全等图形，而由同一张底片冲洗出来的五寸照片和七寸照片 全等图形（填“是”或“不是”）.3．如图，△ABC 与△DBC 能够完全重合，则△ABC 与△DBC 是____________，表示为△ABC ____△DBC ．4．如图，已知△ABC ≌△BAD ，BC =AD ，写出其他的对应边 和对应角 ．5．如图所示，ABC ADE △≌△，BC 的延长线交DA 于F ，交DE 于G ，105ACB AED ∠=∠=o ，15CAD ∠=o ，30B D ∠=∠=o ，则1∠的度数为 ．6．如图，已知AB BD ⊥，垂足为B ，ED BD ⊥，垂足为D ，AB CD =，BC DE =，则ACE ∠＝___________o ．7．如图，已知AF BE =，A B ∠=∠，AC BD =，经分析 ≌ ．此时有F ∠= ．A B C DE F （第1题） A B C（第3题） A BC OD （第4题）（第5题）（第6题）CEF（第7题）ACODBB A1 2（第8题） （第9题）8．如图所示，AB ，CD 相交于O ，且AO ＝OB ，观察图形，图中已具备的另一相等的条件是________，联想到SAS ，只需补充条件________，则有△AOC ≌△________． 9．如图所示，有一块三角形的镜子，小明不小心弄破裂成1、2两块，现需配成同样大小的一块．为了方便起见，需带上________块，其理由是__________． 10．如图，把两根钢条AA '，BB '的中点O 连在一起，可以做成一个测量工件内槽宽的工具（工人把这种工具叫卡钳）只要量出A B ''的长度，就可以知道工件的内径AB 是否符合标准，你能简要说出工人这样测量的道理吗？ ． 二、选择题（每题3分，共24分）11．下列说法：①全等图形的形状相同、大小相等；②全等三角形的对应边相等；③全等三角形的对应角相等；④全等三角形的周长、面积分别相等，其中正确的说法为（ ） Ａ．①②③④ Ｂ．①③④ Ｃ．①②④ Ｄ．②③④ 12．如果D 是ABC △中BC 边上一点，并且ADB ADC △≌△，则ABC △是（）Ａ．锐角三角形Ｂ．钝角三角形Ｃ．直角三角形Ｄ．等腰三角形13．一个正方形的侧面展开图有（ ）个全等的正方形.A ．2个B ．3个C ．4个D ．6个 14．对于两个图形，给出下列结论：①两个图形的周长相等；②两个图形的面积相等；③两个图形的周长和面积都相等；④两个图形的形状相同，大小也相等．其中能获得这两个图形全等的结论共有（ ）A ．1个B ．2个C ．3个D ．4个15．如图，在ABC △和DEF △中，已知AB DE =，BC EF =，根据（SAS ）判定ABC DEF △≌△，还需的条件是（ ）Ａ．A D ∠=∠ Ｂ．B E ∠=∠ Ｃ．C F ∠=∠ Ｄ．以上三个均可以16．下面各条件中，能使△ABC ≌△DEF 的条件的是（ ）Ａ．AB ＝DE ，∠A ＝∠D ，BC ＝EF Ｂ．AB ＝BC ，∠B ＝∠E ，DE ＝EF C ．AB ＝EF ，∠A ＝∠D ，AC ＝DF Ｄ．BC ＝EF ，∠C ＝∠F ，AC ＝DF 17．如图，AD BC ，相交于点O ，OA OD =，OB OC =．下列结论正确的是（ ）A ．AOB DOC △≌△． B ．ABO DOC △≌△ C ．A C ∠=∠D ．B D ∠=∠（第10题）18．如图，已知AB AC =，AD AE =，BAC DAE ∠=∠．下列结论不正确的有（ ）．A ．BAD CAE ∠=∠B ．ABD ACE △≌△C ．AB=BCD ．BD CE = 三、解答题（共46分）19．（7分）找出下列图形中的全等图形．（1） （2） （3） （4） （5） （6）（7） （8） （9） （10） （11） （12）20．（7分）如图，AB =DC ，AC =DB ，求证AB ∥CD ．21．（8分）如图，已知AB ∥DC ，AD ∥BC .证明：（1）AB =CD ；（2）AD =BC ．DCBAABOC A EDB CA D（第15题） （第17题） （第18题）22．（8分）如图，点A B C D ，，，在一条直线上，△ABF ≌△DCE ，你能得出哪些结论?（请写出三个以上的结论）23．（8分）如图，点D E ，分别在AB AC ，上，且AD AE =，BDC CEB ∠=∠．求证：BD CE =．24．（8分）如右图，已知DE ⊥AC ，BF ⊥AC ，垂足分别是E 、F ，AE =CF ，DC ∥AB ，（1）试证明：DE =B F ；（2）连接DF 、BE ，猜想DF 与BE 的关系？并证明你的猜想的正确性．DFCBAE参考答案一、填空题1．80，13 2．是 不是 3．全等三角形，≌ 4．AC =BD ，AB =BA ，∠C =∠D ，∠CAB =∠DBA ，∠ABC =∠BAD 5．60度 6．90 7．ADF BCE △≌△，得F E ∠=∠． 8．∠AOC =∠BOD ，OC =OD ，△BOD 9．1，有两边及其夹角对应相等的两个三角形全等 10．此工具是根据三角形全等制作而成的．由O 是AA '，BB '的中点，可得AO A O '=，BO B O '=，又由于AOB ∠与A OB ''∠是对顶角，可知AOB A OB ''∠=∠，于是根据“SAS ”有AOB A OB ''△≌△，从而A B AB ''=，只要量出A B ''的长度，就可以知道工作的内径AB 是否符合标准二、选择题11．A 12．Ｄ 13．C 14．A 15．B 16．D 17．A 18．C 三、解答题19．（1）和（10），（2）和（12），（4）和（8），（5）和（9）是全等图形 20．略 21．略 22．由△ABF ≌△,DCE 可得到BAF CDE AFB DEC ABF DCE AB DC BF CE AF DE ∠=∠∠=∠∠=∠===，，，，，；AF ED AC BD BF CE =∥，，∥，△AEC ≌△DFB 等 23．略 24．（1）证明 Rt △CDE ≌Rt △AFB ；（2）DF ∥BE 且DF=BE。

全等三角形课后作业题五1．在△ABC中，AC=BC，∠ACB=90°，CE是过C点的一条直线，AD⊥CE于D，BE⊥CE于E，DE=4cm，AD=2cm，则BE=（）A． 2cm B． 4cm C． 6cm或2cm D． 6cm2．在△ABC内部取一点P，使得点P到△ABC的三边的距离相等，则点P应是△ABC的下列哪三条线段的交点（）A．高 B．中线 C．垂直平分线 D．角平分线3．如图，在和中，点在边上，边交边于点. 若，，，则等于（）A． B． C． D．4．如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB，BC于点D，E．将△BDE沿直线DE折叠，得到△B′DE，若B′D，B′E分别交AC于点F，G，连接OF，OG，则下列判断错误的是（）A．△ADF≌△CGEB．△B′FG的周长是一个定值C．四边形FOEC的面积是一个定值D．四边形OGB'F的面积是一个定值5．如图，△ABC中，D是BC的中点，过点D的直线MN交边AC于点M，交AC的平行线BN于点N，DE⊥MN，交边AB于点E，连结EM，下面有关线段BE，CM，EM的关系式正确的是（）A．BE+CM=EM B．BE2+CM2=EM2C．BE+CM﹥EM D．EM－BE=12 MC6．在等腰梯形ABCD 中，∠ABC ＝2∠ACB ，BD 平分∠ABC ，AD ∥BC ，如图所示，则图中的等腰三角形有( )A ． 1个B ． 2个C ． 3个D ． 4个7．如图，AB ∥CD ，BC ∥AD ，AB=CD ，BE=DF ，图中全等的三角形的对数是（ ）A ． 3B ． 4C ． 5D ． 68．如图，已知在ABC 中， CD 是AB 边上的高线， BE 平分ABC ∠，交CD 于点E ， 5BC =， 2DE =，则BCE 的面积等于（ ）．A ． 5B ． 7C ． 10D ． 49．如图是两个全等三角形，图中的字母表示三角形的边长，则1∠的度数是（ ）A ． 54°B ． 60°C ． 66°D ． 76°10．如图，在Rt ΔABC 中，AC=BC ，∠ACB=90°，AD 平分∠B AC ，BE ⊥AD 交AC 的延长线于F ，E 为垂足．则结论：（1）AD=BF ；（2）CF=CD ；（3）AC +CD=AB ；（4）BE=CF ；（5）BF=2BE ，其中正确的结论个数是（ ）．A ． 2B ． 3C ． 4D ． 511．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=48°，则∠AED为°．12．如图，FD⊥AO于D，FE⊥BO于E，下列条件：①OF是∠AOB的平分线；②DF=EF；③DO=EO；④∠OFD=∠OFE．其中能够证明△DOF≌△EOF的条件的个数有__个．13．如图，中，P、Q分别是BC、AC上的点，作，，垂足分别是R、S，若，，下面四个结论：①；②；③≌；④AP垂直平分其中正确结论的序号是______ 请将所有正确结论的序号都填上．14．如图，∠ACB＝90°，AC＝BC，BD⊥CE，AE⊥CE，垂足分别是D，E，BD＝5，DE＝3.则△BDC的面积是__________.15．如果∠α和∠β互补，且∠α>∠β，则下列表示的式子：①90°-∠β②∠α-90°③12（∠α+∠β）④12（∠α-∠β），其中，能表示∠β的余角的是____________（填序号）.16．如图，若∠1=∠2，加上一个条件__，则有△AOC≌△BOC．17．如图，平分，那么等于______．18．如图，已知AB=AD ，∠BAE=∠DAC ，要使△ABC ≌△ADE ，可补充的条件是________（写出一个即可）19．如图，△ABC 中，AB=4,BC=3,∠ABC=45°，BC 、AC 两边上的高AD 与BE 相交于点F ，连接CF ，则线段CF 的长=_____________．20．在△ABC 中，∠C=90°，BC=16，∠BAC 的平分线交BC 于D ，且BD ：DC=5：3，则D 到AB 的距离为_____________． 21．如图所示，OM 平分∠AOB ，ON 平分∠COD ，OM ⊥ON ，∠BOC =26°，求∠AOD 的度数.22．如图，已知AB AC ⊥， AB AC =， AD AE =， BD CE =，试猜想AD 与AE 的位置关系并说明理由．23．如图，∠A =∠B ，AE=BE ，点D 在AC 边上，∠1=∠2，AE ，BD 交于点O ；求证：△AEC≌△BED；24．如图，O为直线AB上一点，，OD平分，（1）求出的度数；（2）请通过计算说明OE是否平分.25．在直角中，，，AD，CE分别是和的平分线，AD，CE相交于点F．求的度数；判断FE与FD之间的数量关系，并证明你的结论．26．如图，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在上．（1）求证：AE=AB；（2）若∠CAB=90°，cos∠ADB=，BE=2，求BC的长．27．如图所示，铁路上A，B两站(视为直线上两点)相距14 km，C，D为两村 (可视为两个点)，DA⊥AB于A，CB⊥AB于B，已知DA＝8 km，CB＝6 km，现在要在铁路上建一个土特产品收购站E，使C，D两村到正站的距离相等，则E站应建在距A站多少千米处?28．如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．（1）求证：AD=BE；（2）求∠AEB的度数．。

初中数学人教版八年级上册实用资料12.2三角形全等的判定基础巩固1.(题型三)如图12-2-1，某同学把一块三角形玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是( )______A.带①去B.带②去C.带③去D.带①和②去图12-2-12.(题型一)如图12-2-2，在∆ABC中，AB=AC，BE=CE，则由“SSS”可以判定( )图12-2-2A.∆ABD≌∆ACDB.∆BDE≌∆CDEC.∆ABE≌∆ACED.以上都不对3.(题型一、四)如图12-2-3，∆BDC′是将长方形纸片ABCD沿着BD折叠得到的，图中（包括实线、虚线在内）共有全等三角形( )图12-2-3A.1对B.2对C.3对D.4对4.(题型三)如图12-2-4，点B在射线AE上，∠CAE=∠DAE，∠CBE=∠DBE，AD=8，则AC= ．图12-2-45.(题型二、三、四、五)如图12-2-5，已知AB⊥CF，DE⊥CF，垂足分别为B，E，AB=DE．请你添加一个适当的条件，使∆ABC≌∆DEF．添加的条件是．图12-2-56.(题型三)如图12-2-6,AB∥CD,AD，BC交于点O,EF过点O分别交AB，CD于点E，F，且AE=DF.求证：O是EF的中点．图12-2-67.(题型二)［福建泉州中考］如图12-2-7，∆ABC，∆CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：∆CDA≌∆CEB．图12-2-7能力提升8.(题型一、二)下列说法中，正确的是（）A.两边及一组角对应相等的两个三角形全等B.有两边分别相等，且有一角为30°的两个等腰三角形全等C.两边及其中一边上的中线对应相等的两个三角形全等D.两边及其中一边上的高对应相等的两个三角形全等9.(题型四)如图12-2-8，在∆ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=4，AD=3,则点D到BC的距离是( )图12-2-8A.3B.4C.5D.610.(题型二)如图12-2-9，在∆ABC中，AB=CB，∠ABC=90°，D为AB的延长线上一点，点E在BC边上，且BE=BD，连接AE，DE，DC.图12-2-9（1）求证：∆ABE≌∆CBD.（2）若∠CAE=30°，求∠BDC的度数.11.(题型三)［湖北宜昌中考］杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：如图12-2-10，AB∥OH∥CD，相邻两平行线间的距离相等，AC，BD相交于点O，OD⊥CD，垂足为D，已知AB=20米，请根据上述信息求标语CD的长度．图12-2-1012.(题型四、五)如图12-2-11，CD⊥AB于点D，BE⊥AC于点E，且BD=CE，BE交CD于点O．求证：AO平分∠BAC．图12-2-1113.(题型二、三)如图12-2-12,AB∥CD，OA=OD，AE=DF.求证：EB∥CF.图12-2-1214.(题型四)在数学习题课后，老师布置了一道课后练习题：如图12-2-13，在Rt∆ABC中，AB=BC，∠ABC=90°，BO⊥AC于点O，点P，D分别在AO和BC上，PB=PD，DE⊥AC 于点E.求证：∆BPO≌∆PDE．图12-2-13（1）理清思路，完成解答，本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写本题的证明过程．（2）特殊位置，证明结论：若PB平分∠ABO，其余条件不变．求证：AP=CD．答案基础巩固1. C 解析：③保留了原来三角形的两个角和它们的夹边，可以根据“ASA”来配一块与原来一样的玻璃，所以应带③去．故选C.2. C 解析：∵AB=AC，EB=EC，AE=AE,∴△ABE≌△ACE（SSS）．故选C.3. D 解析：∵△BDC′是将长方形纸片ABCD沿对角线BD折叠得到的，∴△C′DB≌△CDB.∵AB=DC,AD=BC,BD=BD,∴△ABD≌△CDB(SSS)，∴△ABD≌△C′DB．在△ABO和△C′DO中，易知AB=C′D，∠A=∠C′=90°.又∵∠AOB=∠C′OD,∴△ABO≌△C′DO（AAS）．故选D.4. 8 解析：∵∠CBE=∠DBE，∴∠ABC=∠ABD．在△ABC和△ABD中,,,, ABC ABDAB ABCAB DAB∠=∠=∠=∠⎧⎪⎨⎪⎩∴△ABC≌△ABD（ASA），∴AC=AD=8．5. BC=EF（或BF=CE或AC=DF或∠A=∠D或∠C=∠F或AC∥DF，答案不唯一) 解析：∵AB⊥CF，DE⊥CF，∴△ABC和△DEF都是直角三角形．又∵AB=DE，∴可以添加的条件有：BC=EF（或BF=CE），△ABC≌△DEF（SAS）；AC=DF，Rt△ABC≌Rt△DEF （HL）；∠A=∠D，△ABC≌△DEF（ASA）；∠C=∠F(或AC∥DF)，△ABC≌△DEF（AAS）．6. 证明：∵AB∥CD,∴∠EAO=∠FDO,∠AEO=∠DFO.在△AEO和△DFO中,,,, EAO FDOAE DFAEO DFO ∠=∠=∠=∠⎧⎪⎨⎪⎩∴△AEO≌△DFO（ASA）,∴OE=OF. ∴O是EF的中点．7.证明：∵△ABC，△CDE均为等腰直角三角形，且∠ACB=∠DCE=90°,∴CE=CD，BC=AC，∠ACB-∠ACE=∠DCE-∠ACE, ∴∠ECB=∠DCA.在△CEB和△CDA中，,,,BC ACECB DCA EC DC=∠=∠=⎧⎪⎨⎪⎩∴△CEB≌△CDA(SAS)．能力提升8. C 解析：选项A属于“SSA”，不是判定三角形全等的条件，错误；选项B，如图D12-2-1的两个等腰三角形的腰长相等，且有一角为30°,但这两个等腰三角形不全等，错误；选项C可利用“SSS”和“SAS”证明两个三角形全等，正确；选项D中的高有可能在三角形内部，也有可能在三角形外部，是不确定的，不符合全等的条件，D错误．故选C.图D12-2-1图D12-2-29. A 解析：如图D12-2-2，过点D作DE⊥BC，垂足为E,则DE的长即是点D到BC的距离．∵BD平分∠ABC，∴∠ABD=∠EBD．在△ABD和△EBD中，90,,,A DEBABD EBDBD BD∠=∠=︒∠=∠=⎧⎪⎨⎪⎩∴△ABD≌△EBD(AAS),∴DE=AD=3,即点D到BC的距离是3．故选A.10.（1）证明：∵∠ABC=90°，D为AB的延长线上一点，∴∠ABE=∠CBD=90°.在△ABE和△CBD中，,,,AB CBABE CBD BE BD=∠=∠=⎧⎪⎨⎪⎩∴△ABE≌△CBD（SAS）.(2)解：∵AB=CB，∠ABC=90°，∴∠CAB=45°．∵∠CAE=30°，∴∠BAE=∠CAB-∠CAE=45°-30°=15°．∵△ABE≌△CBD，∴∠BCD=∠BAE=15°.∴∠BDC=90°-∠BCD=90°-15°=75°.11. 解：∵AB∥CD，∴∠ABO=∠CDO．∵OD⊥CD，∴∠CDO=90°.∴∠ABO=90°，即OB⊥AB．∵相邻两平行线间的距离相等，∴OD=OB．在△ABO和△CDO中，,,,ABO CDOAOB COD OB OD∠=∠∠=∠=⎧⎪⎨⎪⎩∴△ABO≌△CDO（ASA），∴CD=AB=20米．12. 证明：∵OD⊥AB，OE⊥AC，∴∠BDO=∠CEO=90°.在△BOD和△COE中，90,,,BDO CEOBOD COEBD CE∠=∠=︒∠=∠=⎧⎪⎨⎪⎩∴△BOD≌△COE（AAS），∴OD=OE．在Rt△AOD和Rt△AOE中，OA=OA, OD=OE,∴Rt△AOD≌Rt△AOE（HL）,∴∠DAO=∠EAO，即AO平分∠BAC．13. 证明：∵AB∥CD（已知），∴∠3=∠4(两直线平行，内错角相等).在△DCO和△ABO中，34(),,12, OD OA∠=∠=∠=∠⎧⎪⎨⎪⎩已证（已知）（对顶角相等）∴△DCO≌△ABO(ASA),∴OC=OB(全等三角形的对应边相等). ∵AE=DF,OA=OD,∴OD+DF=OA+AE,即OF=OE.在△COF和△BOE中，(),(),12, OC OBOF OE==∠=∠⎧⎪⎨⎪⎩已证已证（对顶角相等）∴△COF≌△BOE(SAS),∴∠F=∠E(全等三角形的对应角相等).∴EB∥CF（内错角相等，两直线平行）.14. 证明：（1）∵PB=PD，∴∠2=∠PBD．∵AB=BC，∠ABC=90°，∴∠C=45°．∵BO⊥AC，∴∠1=45°.∴∠1=∠C=45°．∵∠3=∠PBC-∠1，∠4=∠2-∠C，∴∠3=∠4．∵BO⊥AC，DE⊥AC，∴∠BOP=∠PED=90°．在△BPO和△PDE中，34,,,BOP PED BP PD∠=∠∠=∠=⎧⎪⎨⎪⎩∴△BPO≌△PDE（AAS）.（2）由（1）得,∠3=∠4．∵BP平分∠ABO，∴∠ABP=∠3.∴∠ABP=∠4．在△ABP和△CPD中，,4,,A CABPPB PD∠=∠∠=∠=⎧⎪⎨⎪⎩∴△ABP≌△CPD（AAS），∴AP=CD．。

人教版八年级上册数学第十二章全等三角形含答案一、单选题(共15题，共计45分)1、如图，在∠AOB的两边上，分别取OM=ON，再分别过点M、N作OA，OB的垂线，交点为P，画射线OP，则OP平分∠AOB的依据是（）A.SASB.SSSC.AASD.HL2、如图，是的角平分线，于点，于点，连接交于．有以下三个结论：①；②；③当时，四边形是正方形；④．其中正确的是（）A.②③B.②④C.①③④D.②③④3、PA，PB，CD是⊙O的切线，A，B，E是切点，CD分别交PA，PB于C，D两点，若∠APB＝40°，则∠COD的度数是（）A.50°B.60°C.70°D.75°4、下列命题是假命题的是（）A.线段垂直平分线上的点到线段两端的距离相等B.三角形的一个外角等于与它不相邻的两个内角的和C.有一个外角是120°的等腰三角形是等边三角形D.有两边和一角对应相等的两个三角形全等5、如图，D、E分别是△ABC的边AC、BC上的点，且△ADB≌△EDB≌△EDC，则∠C的度数为（）A.15ºB.20ºC.25ºD.30º6、两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO=CO= AC；③△ABD≌△CBD，其中正确的结论有（）A.0个B.1个C.2个D.3个7、下列说法：①三角形的三条高一定都在三角形内②有一个角是直角的四边形是矩形③有一组邻边相等的平行四边形是菱形④两边及一角对应相等的两个三角形全等⑤一组对边平行，另一组对边相等的四边形是平行四边形其中正确的个数有（）A.1个B.2个C.3个D.4个8、已知△ABC≌△A′C′B′，∠B与∠C′，∠C与∠B′是对应角，有下列4个结论：①BC=C′B′；②AC=A′B′；③AB=A′B′；④∠ACB=∠A′B′C′，其中正确的结论有（）A.1个B.2个C.3个D.4个9、如图，AD是的中线，E是AD上一点，连接BE并延长交AC于点F，若EF=AF，BE=7.5，CF=6，则EF=( ).A.2.5B.2C.1.5D.110、具有下列条件的两个等腰三角形，不能判断它们全等的是（）A.两腰对应相等B.底边、一腰对应相等C.顶角、一腰对应相等 D.一底角、底边对应相等11、如图,已知AB=AD,添加一个条件后,仍然不能判定△ABC≌△ADC的是( )A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°12、如图，C为线段上一动点（不与A、E重合），在同侧分别作等边和等边，与交于点O，与交于点P，与交于点Q，连接，以下五个结论：①；②；③；④；⑤，恒成立的结论有（）A.①③⑤B.①③④⑤C.①②③⑤D.①②③④⑤13、在△ABC内部取一点P，使得点P到△ABC的三边的距离相等，则点P应是△ABC的下列哪三条线段的交点（）A.高B.中线C.垂直平分线D.角平分线14、在直线l上依次摆放着七个正方形(如图所示)。

人教版八年级上册数学第十二章全等三角形含答案一、单选题(共15题，共计45分)1、如图所示，在平面直角坐标系中，点A（3，1），点P在x轴上，若以P、O、A为顶点的三角形是等腰三角形，则满足条件的点 P 共有（）A.2 个B.3 个C.4 个D.5 个2、下列可使两个直角三角形全等的条件是（）A.一条边对应相等B.斜边和一直角边对应相等C.一个锐角对应相等D.两个锐角对应相等3、如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=2，AB=6，则△ABD的面积是( )A.4B.6C.8D.124、一块三角形玻璃被小红碰碎成四块，如图5,小红只带其中的两块去玻璃店，买了一块和以前一样的玻璃，你认为她带哪两块去玻璃店了（）A.带其中的任意两块B.带1，4或3，4就可以了C.带1，4或2，4就可以了D.带1，4或2，4或3，4均可5、如图，已知▱ABCD中，∠DBC＝45°，DE⊥BC于E，BF⊥CD于F，DE、BF相交于H，BF、AD的延长线相交于G，下面结论：①DB＝BE；②∠A＝∠BHE；③AB＝BH；④△BHD∽△BDG.其中正确的结论是（）A.①②③④B.①②③C.①②④D.②③④6、如图，点P是AB上任意一点，∠ABC=∠ABD，还应补充一个条件，才能推出△APC≌△APD．从下列条件中补充一个条件，不一定能推出△APC≌△APD的是（）A.BC=BD；B.AC=AD；C.∠ACB=∠ADB；D.∠CAB=∠DAB7、如图，CE⊥AB，BD⊥AC，垂足分别为E、D，BD、CE交于点O，AB＝AC，∠B ＝20°，则∠AOD＝（）A.20°B.40°C.50°D.55°8、如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（）A.1处B.2处C.3处D.4处9、如图，△ABC的面积为1.5cm2， AP垂直∠B的平分线BP于P，则△PBC的面积为（）A.1cm 2B.0.75 cm 2C.0.5cm 2D.0.25cm 210、下列结论正确的是（）A.面积相等的两个三角形全等B.等边三角形都全等C.底边和顶角对应相等的等腰三角形全等D.两个等腰直角三角形全等11、如图,点P是∠BAC内一点,且到AB,AC的距离PE,PF相等,则△PEA≌△PFA 的依据是( )A.HLB.ASAC.SSSD.SAS12、如图，已知∠C=∠D，∠ABC=∠BAD，AC与BD相交于点O，OE⊥AB于点E，则图中全等的三角形有( )A.1对B.2对C.3对D.4对13、如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P 2， P3， P4四个点中找出符合条件的点P，则点P有（）A.1个B.2个C.3个D.4个14、下列所叙述的图形中，全等的两个三角形是（）A.含有45°角的两个直角三角形B.腰相等的两个等腰三角形C.边长相等的两个等边三角形D.一个钝角对应相等的两个等腰三角形15、在△ABC和△DEF中，AB=DE，∠A=∠D，若△ABC≌△DEF，则还需要（）A.∠B=∠EB.∠C=∠FC.AC=DFD.以上三种情况都可以二、填空题(共10题，共计30分)16、如图，在平面直角坐标系中，反比例函数（x＞0）与正比例函数y=kx、（k＞1）的图像分别交于点A、B，若∠AOB＝45°,则△AOB的面积是________.17、如图，在⊙O的内接四边形ABCD中，AB=3，AD=5，∠BAD=60°，点C为弧BD的中点，则AC的长是________.18、如图所示，在△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线，则∠C=________．19、直线y=-2x+2交x轴于点A，交y轴于点B，若点C在第一象限，且ABC是等腰直角三角形，则点C的坐标是________20、如图城南中学八年级学习小组发现：当角平分线遇上平行线会出现等腰三角形。

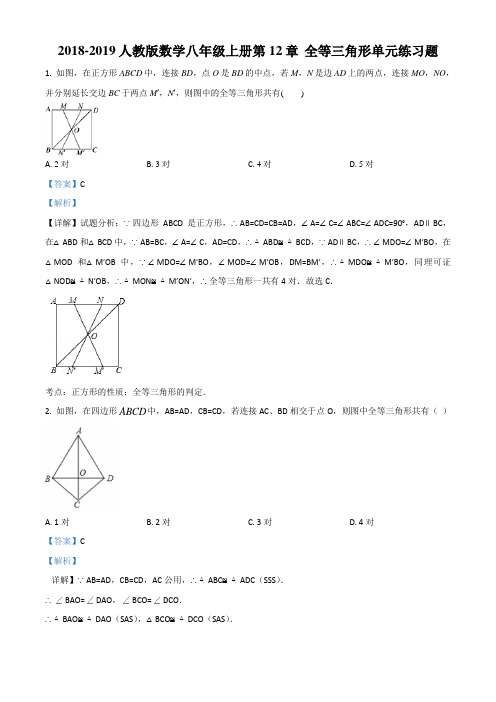
全等三角形定义和全等三角形性质1. （呼伦贝尔中考）如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（）A. 20°B. 30°C. 35°D. 40°2. 如图，已知点D在AC上，点B在AE上，△ABC≌△ADE，且∠A=∠ABD.若∠A：∠C=5：3，则∠BDE等于（）A. 25°B. 20°C. 24°D. 15°3. 如图所示，已知△ABC≌△ADE，BC的延长线交DE于F，∠B=∠D=25°，∠ACB=∠AED=105°，∠DAC=10°，则∠DFB为（）A. 40°B. 50°C. 55°D. 60°4. 如图，△ABC≌△DEF，∠A=∠D，∠B=∠DEF，则下列结论错误的是（）A. AB=DEB. AC=DFC. BE=FCD. ∠B=∠F5. 如图所示，在△ABC中，∠A：∠B：∠C=3：5：10，又△A′B′C′≌△ABC，则∠BCA′：∠BCB′等于（）A. 1：2B. 1：3C. 2：3D. 1：46. 如图，已知△ABC≌△ADE，若∠ABC=70°，∠DAE=80°，则∠C的度数是（）A. 30°B. 40°C. 70°D. 80°7. 如图，△ABC≌△ADE，若D、B为对应顶点，AB=5cm，AC=8cm，DE=7cm，则BC= ，△ADE的周长=8. 如图，Rt△ABC中，∠ACB=90°，∠A=20°，△ABC≌△A′B′C，若A′B′恰好经过点B，A′C交AB于D，则∠BDC的度数为9. 如图，在△ABC中，D、E分别是边AC、BC上的点，若△ADB≌△EDB≌△EDC，AB=10cm，则BC= cm.10. 如图，D、A、E在一条直线上，△ADC≌△AEB，∠BAC=40°，∠D=45°求：（1）∠B的度数；（2）∠BMC的度数.11. 如图，已知△EFG≌△NMH，∠F与∠M是对应角.（1）写出相等的线段与角.（2）若EF=2.1cm，FH=1.1cm，HM=3.3cm，求MN和HG的长度.12. 如图，点A，B，C，D在一条直线上，△ABF≌△DCE.你能得出哪些结论？（请写出三个以上的结论）全等三角形定义和全等三角形性质课后作业参考答案1. 解析：本题根据全等三角形的性质并找清全等三角形的对应角即可.解：∵△ACB ≌△A′CB′，∴∠ACB=∠A′CB′，即∠ACA′+∠A′CB=∠B′CB+∠A′CB，∴∠ACA′=∠B′CB，又∠B′CB=30°∴∠ACA′=30°.故选：B.2. 解析：根据全等三角形对应边相等可得AB=AD ，根据等角对等边可得AD=BD ，从而得到AB=BD=AD ，判断出△ABD 是等边三角形，根据等边三角形的性质可得∠A=60°，再求出∠C ，根据全等三角形对应角相等可得∠E=∠C ，然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.解：∵△ABC ≌△ADE ，∴AB=AD ，∵∠A=∠ABD ，∴AD=BD ，∴AB=BD=AD ，∴△ABD 是等边三角形，∴∠A=60°，∵∠A ：∠C=5：3，∴∠C=53×60°=36°，∵△ABC ≌△ADE ， ∴∠E=∠C ，在△BDE 中，∠BDE=∠ABD-∠E=60°-36°=24°.故选C.3. 解析：设AD 与BF 交于点M ，要求∠DFB 的大小，可以在△DFM 中利用三角形的内角和定理求解，转化为求∠AMC 的大小，再转化为在△ACM 中求∠ACM 就可以.解：设AD 与BF 交于点M ，∵∠ACB=105，∴∠ACM=180°-105°=75°，∠AMC=180°-∠ACM-∠DAC=180°-75°-10°=95°，∴∠FMD=∠AMC=95°，∴∠DFB=180°-∠D-∠FMD=180°-95°-25°=60°.故选D.4. 解析：两三角形全等，根据全等三角形的性质，利用条件推出BC=EF和AC=DF，然后依据选项分析三角形即可.解：∵△ABC≌△DEF，∴∠A=∠D、∠B=∠DEF，∴AB=DE，AC=DF，BC=EF，∴BC-EC=EF-EC，即BE=FC，A，B，C都是正确的；∠F与∠B不是对应角，∴∠B=∠F是错误的，D选项错误.故选D5. 解析：设∠A=3k，∠B=5k，∠C=10k，根据全等三角形对应角相等可得∠A′CB′=∠ACB=10k，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCB′=8k，然后求出∠A′CB=2k，求出比值即可.解：∵∠A：∠B：∠C=3：5：10，∴设∠A=3k，∠B=5k，∠C=10k，∵△A′B′C′≌△ABC，∴∠A′CB′=∠ACB=10k，在△ABC中，∠B′CB=∠A+∠B=3k+5k=8k，∴∠A′CB=∠A′CB′-∠B′CB′=10k-8k=2k，∴∠BCA′：∠BCB′=2k：8k=1：4.故选D.6. 解析：根据全等三角形的性质求出∠BAC的度数，在△ABC中，根据三角形的内角和定理求出即可.解：∵△ABC≌△ADE，∠ABC=70°，∠DA E=80°，∴∠BAC=∠DAE=80°，∴∠C=180°-∠ABC-∠BAC=180°-70°-80°=30°.故选A.7. 解析：根据全等三角形对应边相等可得BC=DE，再求出△ABC的周长，然后根据全等三角形的周长相等解答.解：∵△ABC≌△ADE，∴BC=DE=7cm，∴△ABC的周长=5+8+7=20cm，∴△ADE的周长=20cm.故答案为：7cm；20cm.8. 解析：根据直角三角形两锐角互余求出∠ABC，根据全等三角形对应边相等可得BC=B′C，全等三角形对应角相等可得∠B′=∠ABC，然后根据等腰三角形的性质求出∠BCB′，再求出∠BCD，然后根据三角形的内角和定理列式计算即可得解.解：∵∠ACB=90°，∠A=20°，∴∠ABC=90°-20°=70°，∵△ABC≌△A′B′C，∴BC=B′C，∠B′=∠ABC=70°，∴∠BCB′=180°-70°×2=40°，∴∠BCD=90°-40°=50°，在△BCD中，∠BDC=180°-70°-50°=60°.故答案为：60.9. 解析：根据全等三角形的性质得出AB=BE=CE=10cm，即可求出答案.解：∵△ADB≌△EDB≌△EDC，AB=10cm，∴AB=BE=CE=10cm，∴BC=BE+CE=20cm，故答案为：20.10. 解析：（1）根据全等三角形对应角相等可得∠BAE=∠CAD，然后求出∠BAD，再求出∠CAD，再根据三角形的内角和定理求出∠C，然后根据全等三角形对应角相等可得∠B=∠C；（2）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BMC=∠BAC+∠C，代入数据计算即可得解.解：（1）∵△ADC≌△AEB，∴∠BAE=∠CAD ，∵D 、A 、E 在一条直线上，∴∠BAD=21（180°-∠BAC ）=21×（180°-40°）=70°， ∴∠CAD=∠BAD+∠BAC=70°+40°=110°，在△ACD 中，∠C=180°-∠CAD-∠D=180°-110°-45°=25°，又∵△ADC ≌△AEB ，∴∠B=∠C=25°；（2）由三角形的外角性质，∠BMC=∠BAC+∠C ，=40°+25°，=65°.11. 解析：（1）根据△EFG ≌△NMH ，∠F 与∠M 是对应角可得到两个三角形中对应相等的三边和三角；（2）根据（1）中的对等关系即可得MN 和HG 的长度.解：（1）∵△EFG ≌△NMH ，∠F 与∠M 是对应角，∴EF=NM ，EG=NH ，FG=MH ，∠F=∠M ，∠E=∠N ，∠EGF=∠NHM ，∴FH=GM ，∠EGM=∠NHF ；（2）∵EF=NM ，EF=2.1cm ，∴MN=2.1cm ；∵FG=MH ，FH+HG=FG ，FH=1.1cm ，HM=3.3cm ，∴HG=FG-FH=HM-FH=3.3-1.1=2.2cm.12. 解析：本题要灵活运用全等三角形的性质.两个三角形为全等三角形，则对应边相等，对应角相等.解：∵△ABF ≌△DCE∴∠BAF=∠CDE ，∠AFB=∠DEC ，∠ABF=∠DCE ，AB=DC ，BF=CE ，AF=DE ；∴AF ∥ED ，AC=BD ，BF ∥CE.。

人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析一、选择题（每小题3分，共30分） 1.下列说法正确的是（ ）A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等 2. 如图所示，a,b,c 分别表示△ABC 的三边长，则下面与△ABC 一定全等的三角形是（ ）3.如图所示，已知△ABE ≌△ACD ，∠1=∠2，∠B=∠C ， 下列不正确的等式是（ ） B.∠BAE=∠CADA.AB=AC C.BE=DC D.AD=DE 4. 在△ABC 和△A /B /C /中,AB=A /B /,∠B=∠B /,补充条件后仍不一定能保证△ABC ≌△A /B /C /,则补充的这个条件是( )A ．BC=B /C / B ．∠A=∠A / C ．AC=A /C /D ．∠C=∠C / 5.如图所示，点B 、C 、E 在同一条直线上，△ABC 与△CDE都是等边三角形，则下列结论不一定成立的是（ ）A.△ACE ≌△BCDB.△BGC ≌△AFCC.△DCG ≌△ECFD.△ADB ≌△CEA6. 要测量河两岸相对的两点A,B 的距离，先在AB 的垂线BF 上取两点C,D ，使CD=BC ，再作出BF 的垂线DE ，使A,C,E 在一条直线上（如图所示），可以说明△EDC ≌△ABC ，得ED=AB ，因此测得ED 的长就是AB 的长，判定△EDC ≌△ABC 最恰当的理由是（ ） 第3题图第5题图 第2题图第6题图AB C DA.边角边B.角边角C.边边边D.边边角7.已知：如图所示，AC=CD ，∠B=∠E=90°，AC ⊥CD ，则不正确的结论是（ ）A ．∠A 与∠D 互为余角B ．∠A=∠2C ．△ABC ≌△CED D ．∠1=∠28. 在△ABC 和△FED 中，已知∠C=∠D ，∠B=∠E ，要判定这两个三角形全等，还需要条件（ ） A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F 9.如图所示，在△ABC 中，AB=AC ，∠ABC 、∠ACB 的平分线BD ，CE 相交于O 点，且BD 交AC 于点D ，CE 交AB 于 点E ．某同学分析图形后得出以下结论：①△BCD ≌△CBE ； ②△BAD ≌△BCD ；③△BDA ≌△CEA ；④△BOE ≌△COD ；⑤△ACE ≌△BCE ，上述结论一定正确的是（ ） A.①②③ B.②③④ C.①③⑤ D.①③④10、下列命题中：⑴形状相同的两个三角形是全等形；⑵在两个三角形中，相等的角是对应角，相等的边是对应边；⑶全等三角形对应边上的高、中线及对应角平分线分别相等，其中真命题的个数有( ) A 、3个 B 、2个 C 、1个 D 、0个二、填空题（每题3分，共21分）11．如图６，ＡＣ＝ＡＤ，ＢＣ＝ＢＤ，则△ＡＢＣ≌ ；应用的判定方法是 ．12．如图７，△ＡＢＤ≌△ＢＡＣ，若ＡＤ＝ＢＣ，则∠ＢＡＤ的对应角为 ．13．已知ＡＤ是△ＡＢＣ的角平分线，ＤＥ⊥ＡＢ于Ｅ，且ＤＥ＝３cm ，则点Ｄ到ＡＣ的距离为 ．Ｂ Ｃ ＤＡ 图6 D O CBA 图8 A D CB图7 第9题图 第7题图14．如图８，ＡＢ与ＣＤ交于点Ｏ，ＯＡ＝ＯＣ，ＯＤ＝ＯＢ，∠ＡＯＤ＝ ，根据 可得△ＡＯＤ≌△ＣＯＢ，从而可以得到ＡＤ＝ ．15．如图９，∠Ａ＝∠Ｄ＝９０°，ＡＣ＝ＤＢ，欲使ＯＢ＝ＯＣ，可以先利用“ＨＬ”说明 ≌ 得到ＡＢ＝ＤＣ，再利用“ ”证明△ＡＯＢ≌ 得到ＯＢ＝ＯＣ． 16．如果两个三角形的两条边和其中一边上的高分别对应相等，那么这两个三角形的第三边所对的角的关系是 ．17．如图10，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃．那么最省事的办法是带________去配，这样做的数学依据是是 ． 三、解答题（共29分）18. （6分）如右图，已知△ABC 中，AB ＝AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由．解： ∵AD 平分∠BAC∴∠________＝∠_________（角平分线的定义）在△ABD 和△ACD 中⎪⎪⎩⎪⎪⎨⎧∴△ABD ≌△ACD （ ） 19． （8分）如图，已知△≌△是对应角．（1）写出相等的线段与相等的角；（2）若EF=2.1 cm ，FH=1.1 cm ，HM=3.3 cm ，求MN和HG 的长度.第19题图图10 DCBA20．（7分）如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BC＝CD，过D作DE∥AB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你说明道理．21．（8分）已知AB∥DE，BC∥EF，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．四、解答题（共20分）22．（10分）已知：BE⊥CD，BE＝DE，BC＝DA，求证：①△BEC≌△DAE；②DF⊥BC．B C EF A23．（10分）如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6．12章·全等三角形（详细答案）一、选择题 CBDCD BDCDC二、填空题 11、△ABD SSS 12、∠ABC 13、3cm 14、∠COB SAS CB 15、△ABC △DCB AAS △DOC 16、相等 17、○3 两角和它们的夹边分别相等的两个三角形全等三、解答题18、AD CAD AB=AC ∠BAD=∠CAD AD=AD SAS19、B 解：(1)EF=MN EG=HN FG=MH ∠F=∠M ∠E=∠N ∠EGF=∠MHN (2)∵△EFG ≌△NMH ∴MN=EF=2.1cm∴GF=HM=3.3cm ∵FH=1.1cm ∴HG=GF －FH=3.3－1.1=2.2cm 20、解：∵DE ∥AB ∴∠A=∠E在△ABC 与△CDE 中∠A=∠E BC=CD∠ACB=∠ECD∴△ABC ≌△CDE(ASA)∴AB=DE21、证明：∵AB ∥DE∴∠A=∠EDF∵BC ∥EFCA∴∠ACB=∠F∵AD=CF∴AC=DF在△ABC与△DEF中∠A=∠EDFAC=DF∠ACB=∠F△ABC≌△DEF(ASA)四、解答题22、证明：①∵ＢＥ⊥ＣＤ∴∠ＢＥＣ＝∠ＤＥＡ＝９０°在Ｒｔ△ＢＥＣ与Ｒｔ△ＤＥＡ中ＢＣ＝ＤＡＢＥ＝ＤＥ∴Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ（ＨＬ）②∵Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ∴∠Ｃ＝∠ＤＡＥ∵∠ＤＥＡ＝９０°∴∠Ｄ＋∠ＤＡＥ＝９０°∴∠Ｄ＋∠Ｃ＝９０°∴∠ＤＦＣ＝９０°∴ＤＦ⊥ＢC23、证明：在△ABC与△ADC中1=∠2AC=AC3=∠4∴△ABC≌△ADC(ASA)∴CB=CD在△ECD与△ECB中CB=CD∠3=∠4CE=CE∴△ECD≌△ECB(SAS)∴∠5=∠6第十二章全等三角形一、填空题（每小题4分,共32分）.1．已知：///ABC A B C ∆∆≌，/A A ∠=∠，/B B ∠=∠，70C ∠=︒，15AB cm =，则/C ∠=_________，//A B =__________．2．如图1，在ABC ∆中，AB=AC ，AD ⊥BC 于D 点，E 、F 分别为DB 、DC 的中点，则图中共有全等三角形_______对．图1 图2 图33． 已知△ABC ≌△A ′B ′C ′，若△ABC 的面积为10 cm 2，则△A ′B ′C ′的面积为______ cm 2，若△A ′B ′C ′的周长为16 cm ，则△ABC 的周长为________c m ． 4． 如图2所示，∠1=∠2，要使△ABD ≌△ACD ，需添加的一个条件是________________(只添一个条件即可)．5．如图3所示，点F 、C 在线段BE 上，且∠1=∠2，BC =EF ，若要使△ABC ≌△DEF ，则还需补充一个条件________，依据是________________．6．三角形两外角平分线和第三个角的内角平分线_____一点，且该点在三角形______部． 7．如图4，两平面镜α、β的夹角 θ，入射光线AO 平行于β，入射到α上，经两 次反射后的出射光线CB 平行于α，则角θ等于________．8．如图5，直线AE ∥BD ，点C 在BD 上，若AE ＝4，BD ＝8，△ABD 的面积为16，则ACE △ 的面积为______．二、选择题（每小题4分,共24分） 9．如图6，AE ＝AF ，AB ＝AC ，E C 与B F 交于点O ，∠A ＝600，∠B ＝250，则∠E OB 的度数为（ ）A 、600B 、700C 、750D 、85010．△ABC ≌△DEF ，且△ABC 的周长为100 cm ，A 、B 分别与D 、E 对应，且AB ＝35 cm ，DF =30 cm ，则EF 的长为( ) A ．35 cm B ．30 cm C ．45 cm D ．55 cm11．图7是一个由四根木条钉成的框架，拉动其中两根木条后，它的形状将会改变，若固定其形状，下列有四种加固木条的方法，不能固定形状的是钉在________两点上的木条．( )A ．A 、FB ．C 、E C ．C 、AD ．E 、F12．要测量河两岸相对的两点A 、B 的距离，先在AB 的垂线BF 上取两点C 、D ，使CD= BC ，再定出BF 的垂线DE ，使A 、C 、E 在一条直线上，可以证明△EDC ≌△ABC ， 得到ED=AB ，因此测得ED 的长就是AB 的长（如图8），判定△EDC ≌△ABC 的理由是（ ）NAMC B图7 图8 图9 图10A．边角边公理 B．角边角公理； C．边边边公理 D．斜边直角边公理13．如图9，在△ABC中，∠A:∠B:∠C=3:5:10，又△MNC≌△ABC，则∠BCM：∠BCN等于（）A．1:2 B．1:3C．2:3 D．1:414．如图10，P是∠AOB平分线上一点，CD⊥OP于F，并分别交OA、OB于CD，则CD_____P点到∠AOB两边距离之和．( )A．小于B．大于C．等于D．不能确定三、解答题（共46分）中，∠ACB=90°，延长BC至B'，使15．已知如图11，ABCC B'=BC，连结A B'．求证：△AB B'是等腰三角形．图11第十二章全等三角形。

人教版八年级上册数学第十二章全等三角形含答案一、单选题(共15题，共计45分)1、用尺规作已知角的平分线的理论依据是（）A.SAS．B.AASC.SSSD.ASA2、如图，△ABC中，AB＝5，AC＝4，以点A为圆心，任意长为半径作弧，分别交AB、AC于D和E，再分别以点D、E为圆心，大于二分之一DE为半径作弧，两弧交于点F，连接AF并延长交BC于点G，GH⊥AC于H，GH＝2，则△ABG的面积为（）A.4B.5C.9D.103、如图，在中，，，D为BC的中点，，垂足为过点B作交DE的延长线于点F，连接CF，现有如下结论：平分；；；；．其中正确的结论有A.5个B.4个C.3个D.2个4、已知∠AOB，用尺规作一个角等于已知角∠AOB的作图痕迹如图所示，则判断∠AOB= 所用到的三角形全等的判断方法是（）A.SASB.ASAC.AASD.SSS5、如图所示，点P是边长为2的正方形ABCD的对角线BD上的动点，过点P分别作PE⊥BC于点E，PF⊥DC于点F，连接AP并延长，交射线BC于点H，交射线DC于点M，连接EF交AH于点G，当点P在BD上运动时（不包括B、D两点），以下结论中：①MF＝MC；②AP＝EF；③AH⊥EF；④AP2＝PM•PH；⑤EF的最小值是．其中正确结论有（）A.2个B.3个C.4个D.5个6、判断两个直角三角形全等的方法不正确的有（）A.两条直角边对应相等B.斜边和一锐角对应相等C.斜边和一条直角边对应相等D.两个锐角对应相等7、如图，△ABC的面积为1cm2， AP垂直∠B的平分线BP于P，则△PBC的面积为（）A. B. C. D.8、如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG.则下列结论正确的是（）①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=122.5°;④BC+FG=1.5A.①②③B.①②C.②③④D.①②③④9、如图，一块三角形玻璃不小心摔碎成如图三片，只需带上其中的一片，玻璃店的师傅就能重新配一块与原来相同的三角形玻璃，你知道应带碎玻璃．（）A.③B.②C.①D.都不行10、如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（）A.y=B.y=C.y= x 2D.y=11、如图，边长为24的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连结HN.则在点M运动过程中，线段HN长度的最小值是（）A.12B.6C.3D.112、如图，两个三角形是全等三角形，x的值是（）A.30B.45C.50D.8513、如图，∠ABC＝∠DCB.要说明△ABC≌△DCB，需添加的条件不能是（）A.AB＝DCB.∠A＝∠DC.BM＝CMD.AC＝DB14、如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）A.∠A=∠CB.AD=CBC.BE=DFD.AD∥BC15、下列命题是真命题的是（）A.两个锐角的和还是锐角；B.全等三角形的对应边相等；C.同旁内角相等，两直线平行；D.等腰三角形既是轴对称图形，又是中心对称图形．二、填空题(共10题，共计30分)16、如图，等边中，，分别是、边上的一点，且，则________ .17、如图，已知D，E是△ABC中BC边上的两点，且AD=AE，请你再添加一个条件：，使△ABD≌△ACE．________18、在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=15，且BD：DC=3：2，则D到边AB的距离是________19、如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF⊥AB于F．若AC=2，则OF的长为________．20、已知，现将绕点逆时针旋转，使点落在射线上，求作.作法：在上截，以点为圆心，为半径作弧，以点为圆心，为半径作弧，两弧在射线右侧交于点，则即为所求.此作图确定三角形的依据是：________.21、如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E.已知CD=2,则AB的长度等于________.22、如图，课间小明拿着老师的等腰三角板玩，不小心掉到两张凳子之间（凳子与地面垂直），已知，，则两张凳子的高度之和为________.23、已知：如图，在长方形ABCD中，AB＝4，AD＝6.延长BC到点E，使CE＝2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为________秒时，△ABP和△DCE 全等.24、如图，点E，F在线段AD上，且AE=DF，AB∥DC，AB=DC，连接BE，BF，CE，CF，则图中共有全等三角形 ________ 对.25、如图：若△ABE≌△ACF，且AB=5，AE=2，则EC的长为________三、解答题(共5题，共计25分)26、如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC27、已知：△ABC内部一点O到两边AB、AC所在直线的距离相等，且OB=OC．求证：AB=AC．28、如图，已知：AD是BC上的中线，且DF=DE．求证：BE∥CF．29、如图，OM平分∠POQ，MA⊥OP，MB⊥OQ，A，B为垂足，AB交OM于点N．求证：∠OAB=∠OBA．30、如图所示，已知在平行四边形ABCD中，BE=DF．求证：∠DAE=∠BCF．参考答案一、单选题(共15题，共计45分)1、C2、B3、B4、D5、C6、D7、B8、B9、A10、C11、B12、A13、D14、B15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、28、29、30、。

第12章《全等三角形》同步练习班级 学号 姓名 得分一、填空题（每题3分，共30分）1．到一个角的两边距离相等的点都在_________.2．∠AOB 的平分线上一点M ，M 到 OA 的距离为1.5 cm ，则M 到OB 的距离为_________. 3．如图，∠AOB =60°，CD ⊥OA 于D ，CE ⊥OB 于E ，且CD =CE ，则∠DOC=_________.4．如图，在△ABC 中，∠C =90°，AD 是角平分线，DE ⊥AB 于E ，且DE =3 cm ，BD =5 cm ，则BC =_________ cm ．5．如图，已知AB 、CD 相交于点E ，过E 作∠AEC 及∠AED 的平分线PQ 与MN ，则直线MN 与PQ 的关系是_________．6．三角形内一点到三角形的三边的距离相等，则这个点是三角形_________的交点． 7．△ABC 中，∠C =90°，AD 平分∠BAC 交BC 于D ，且BD ：CD =3：2，BC =15cm ，则点D 到AB 的距离是__________． 8．角平分线的性质定理： 角平分线上的点_____________________________． 9．（1）如图，已知∠1 =∠2，DE ⊥AB ， DF ⊥AC ，垂足分别为E 、F ，则DE ____DF ． （2）已知DE ⊥AB ，DF ⊥AC ，垂足分别 为E 、F ，且DE = DF ，则∠1_____∠2．10．直角三角形两锐角的平分线所夹的钝角为_______度．二、选择题（每题3分，共24分）11．如图，OP 平分∠AOB ，PC ⊥OA ，PD ⊥OB ，垂足分别是C 、D ．下列结论中错误的是（ ）A ．PC = PDB ．OC = OD C ．∠CPO = ∠DPO D ．OC = PC12．如图，△ABC 中，∠C = 90°，AC = BC ，AD 是∠BAC 的平分线，DE ⊥AB 于E ，若AC = 10cm ，则△DBE 的周长等于( )A ．10cmB ．8cmC ．6cmD ．9cm13．到三角形三条边的距离都相等的点是这个三角形的（ ）A ．三条中线的交点B ．三条高的交点C ．三条边的垂直平分线的交点D ．三条角平分线的交点（第3题） （第4题） （第5题）21A BCDEF（第9题）A BCDO P（第11题）EDCBA（第14题）14． 如图所示，表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ） Ａ．1处 Ｂ．2处 Ｃ．3处 Ｄ．4处 15．给出下列结论，正确的有（ ）①到角两边距离相等的点，在这个角的平分线上；②角的平分线与三角形平分线都是射线；③任何一个命题都有逆命题；④假命题的逆命题一定是假命题 A ．1个 B ．2个 C ．3个 D ．4个 16．已知，Rt △ABC 中，∠C=90°，AD 平分∠BAC 交BC 于D ，若BC =32，且BD ∶CD =9∶7，则D到AB 的距离为（ ） A ．18 B ．16 C ．14 D ．12 17．两个三角形有两个角对应相等，正确说法是（ ）A ．两个三角形全等B ．两个三角形一定不全等C ．如果还有一角相等，两三角形就全等D ．如果一对等角的角平分线相等，两三角形全等18．如图，OB 、OC 是∠AOD 的任意两条射线，OM 平分∠AOB，ON 平分∠COD ，若∠MON =α，∠BOC=β，则表示∠AOD 的代数式为（ ） A ．2α－β B ．α－βC ．α+βD ．2α三、解答题（共46分）19．（7分）如图，已知OE 、OD 分别平分∠AOB 和∠BOC ，若∠AOB =90°，∠EOD =70°，求∠BOC的度数．20．（7分）已知：有一块三角形空地，若想在空地中找到一个点，使这个点到三边的距离相等，试找出该点．（保留画图痕迹）（第18题）21．（8分）如图，点D 、B 分别在∠A 的两边上，C 是∠A 内一点，AB = AD ，BC = CD ，CE ⊥AD 于E ，CF ⊥AF 于F ． 求证：CE = CF22．（8分）已知：如图，在△ABC 中，∠A =90°，AB = AC ，BD 平分∠ABC ．求证：BC = AB + AD23．（8分）如图，PB 和PC 是△ABC 的两条外角平分线． ①求证：∠BPC =90°-12∠BAC ． ②根据第①问的结论猜想：三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形？24．（8分）如图，BP 是△ABC 的外角平分线，点P 在∠BAC 的角平分线上．求证：CP 是△ABC 的外角平分线．F A B E CD D A P C B A DE参考答案一、填空题1．这个角的平分线上2．1.5cm 3．30°4．8 5．MN⊥PQ 6．三条角平分线7．6cm 8．到角的两边的距离相等9．（1）=（2）= 10．135二、选择题11．D 12．B 13．D 14．D 15．B 16．C 17．D 18．A三、解答题19．50°20．画两个角的角平分线的交点P 21．略22．提示：过点D做DM⊥BC 23．①略；②锐角三角形24．提示：过P作三边AB、AC、BC的垂线段PD、PE、PF。