fluent-有限体积法
- 格式:doc
- 大小:223.50 KB
- 文档页数:6

fluent使用方案-回复fluent使用方案-简介及安装Fluent 是一种在计算流体力学(CFD)模拟中广泛使用的高级软件工具。
它是一个基于有限体积法的求解器,可以用于模拟流体流动、换热和其他相关现象。
Fluent 提供了一个直观和易于使用的用户界面,使用户能够轻松地构建模型、设置边界条件、求解和分析结果。
本文将为您介绍Fluent 的安装步骤,以帮助您开始使用这一强大的工具。
第一步:获取Fluent 软件您可以从Ansys 公司的官方网站上下载Fluent 软件。
请确保您从官方网站下载软件,以确保获得最新版本并避免下载非法或已损坏的副本。
第二步:选择合适的版本和许可证下载Fluent 软件后,您需要选择合适的版本和许可证类型。
Fluent 提供了各种版本,包括个人学术版、企业版和研究版等。
根据您的需求和可用资源选择合适的版本。
第三步:安装Fluent 软件安装Fluent 软件非常简单。
双击下载的安装包,然后按照安装向导的指示进行操作即可。
您可能需要提供一些基本的系统信息和许可证密钥。
请确保您拥有管理员权限或拥有足够的权限来安装软件。
第四步:启动Fluent安装完成后,您可以从开始菜单或桌面图标中启动Fluent 软件。
在启动过程中,您可能需要提供许可证密钥。
Fluent 将在您的计算机上创建一个工作目录,用于存储模型和结果文件。
Fluent 使用方案-模型设置第一步:创建几何模型在Fluent 中,您首先需要创建一个几何模型。
可以通过几何建模软件(如Ansys DesignModeler)导入现有几何模型,也可以使用Fluent 内置的几何建模工具创建几何体。
第二步:定义物理属性在模型中,您需要定义各种物理属性,如流体类型、边界条件和材料属性。
Fluent 提供了广泛的物理模型和材料库,您可以根据需要选择。
第三步:网格划分在模拟之前,您需要划分模型网格。
网格划分对模拟结果和计算效率至关重要。

volume of fluid 有限体积法-回复什么是体积法?体积法是一种流体力学数值计算方法,用于模拟流体的运动和相变过程。
该方法通过将流体区域离散化为小的控制体单元,并基于质量守恒原理,计算每个控制体单元中流体相对于时间的体积变化来描绘流体的行为。
其中,有限体积法(Volume of Fluid,VOF)是体积法的一种经典方法,可以用于描述多相流体的界面和相变现象。
VOF方法在工程领域中广泛应用于模拟液体与气体、固体或其他物质的相互作用,例如液滴碰撞、水波折射、汽车空气动力学等。
VOF方法的基本原理是将流体区域离散化为小的控制体单元,并通过分析不同控制体单元中流体的体积分数来确定物质的分布情况。
控制体单元中的体积分数被定义为该单元的体积中所含物质的体积占比。
在VOF方法中,流体的体积分数通常用0到1之间的数值表示,其中0表示该单元中不含物质,而1表示该单元中完全充满物质。
在模拟过程中,VOF方法通过计算流体控制体单元中物质的体积变化来追踪物质的流动。
其中,计算体积变化的关键是确定流体在两个相邻控制体单元之间的界面位置,也就是所谓的界面重构。
界面重构的目的是为了准确地确定流体界面的位置,以便精确计算流体在不同区域的分布情况。
界面重构的方法有很多种,常用的方法包括Piecewise Linear Interface Calculation(PLIC)、Height Function Method(HFM)和Volume Tracking Method(VTM)等。
这些方法通过分析流体界面的几何特征和体积分数分布,提供了不同的数值算法来计算界面位置。
一旦流体界面的位置确定,VOF方法就可以应用于计算物质的传输和相变过程。
通过求解质量守恒方程和物质守恒方程,可以得到流体的运动方程和相变规律。
这些方程描述了流体在空间中的运动和相互作用,提供了对流体行为进行数值模拟的基础。
在实际应用中,VOF方法可以通过将流体区域进一步划分为更小的控制体单元,提高计算精度。

FLUENT知识点FLUENT是一种计算流体力学(CFD)软件,用于模拟和分析流体流动和热传递的现象。
它由美国公司Ansys开发,已经成为工程和科学领域中最常用的CFD模拟工具之一、下面是一些关于FLUENT软件的知识点。
1. FLUENT的基本原理:FLUENT使用Navier-Stokes方程组来描述流动过程,它基于流体力学和热力学原理。
它可以模拟各种流动情况,包括稳态和非稳态流动、气流和液流、可压缩和不可压缩流体等。
2.网格生成:在FLUENT中,首先需要生成一个计算网格。
网格的划分对于计算结果的准确性和计算速度至关重要。
FLUENT提供了多种网格生成方法,包括结构网格和非结构网格,用户可以根据需要选择适当的网格类型。
3.边界条件和初始条件:在进行流动模拟之前,需要定义合适的边界条件和初始条件。
边界条件包括流体速度、压力和温度等。
初始条件是指模拟开始时的流体状态。
FLUENT提供了多种边界条件和初始条件的设置选项。
4.物理模型:FLUENT支持多种物理模型,包括湍流模型、传热模型、化学反应模型等。
这些物理模型可以根据流动问题的特点进行选择和调整,以获得准确的计算结果。
5. 数值方法:FLUENT使用有限体积法来离散化Navier-Stokes方程组。
它将流场划分为小的控制体积,并在每个控制体积上进行数值解算。
FLUENT提供了多种求解算法和网格收敛策略,以提高计算的准确性和稳定性。
6.模拟结果的后处理:FLUENT可以输出各种流动参数和图形结果,以便分析和解释模拟结果。
用户可以获取流体速度、压力、温度分布等信息,并绘制流线图、剖面图、轮廓图等。
7.多物理场耦合:FLUENT可以进行多物理场的耦合模拟,例如流体-固体的传热问题、流体-结构的耦合问题等。
这些问题可以使用FLUENT软件中的多物理模块来进行建模和求解。
8.并行计算:FLUENT可以利用多核计算机或计算集群进行并行计算,以加快计算速度。
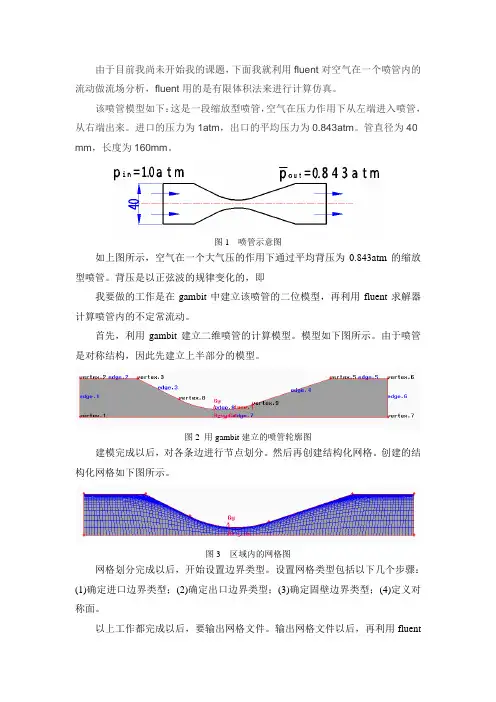
由于目前我尚未开始我的课题,下面我就利用fluent对空气在一个喷管内的流动做流场分析,fluent用的是有限体积法来进行计算仿真。
该喷管模型如下:这是一段缩放型喷管,空气在压力作用下从左端进入喷管,从右端出来。
进口的压力为1atm,出口的平均压力为0.843atm。
管直径为40 mm,长度为160mm。
图1 喷管示意图如上图所示,空气在一个大气压的作用下通过平均背压为0.843atm的缩放型喷管。
背压是以正弦波的规律变化的,即我要做的工作是在gambit中建立该喷管的二位模型,再利用fluent求解器计算喷管内的不定常流动。
首先,利用gambit建立二维喷管的计算模型。
模型如下图所示。
由于喷管是对称结构,因此先建立上半部分的模型。
图2 用gambit建立的喷管轮廓图建模完成以后,对各条边进行节点划分。
然后再创建结构化网格。
创建的结构化网格如下图所示。
图3 区域内的网格图网格划分完成以后,开始设置边界类型。
设置网格类型包括以下几个步骤:(1)确定进口边界类型;(2)确定出口边界类型;(3)确定固壁边界类型;(4)定义对称面。
以上工作都完成以后,要输出网格文件。
输出网格文件以后,再利用fluent进行喷管内流动的仿真计算。
利用fluent进行喷管内流动的仿真计算步骤如下:(1)读入网格文件,读入网格文件以后,将会在信息反馈窗口显示网格的有关信息,如果没有错误就可以继续进行,若有错误,要重新设定gambit中的网格。
(2)下面再检查网格,fluent将会对网格进行各种检查,并将结果在信息反馈窗口中显示出来,其中要特别注意最小体积一项,要确保为正数,否则无法计算。
(3)检查网格没有问题后,要显示网格。
由于显示的网格图形不是整体,而仅仅是图形的一半。
为了更好的显示网格图形,可以利用镜面反射功能,以对称面为镜面,进行对称反射并构成一个整体。
如下图所示:图4 整体区域的网格图(4)设置长度单位及压强单位,由于fluent默认的长度单位是m,要将单位改成mm;再重新设定压强的单位,定义压强的单位为大气压atm,它不是fluent 的默认单位,其默认单位为Pa。

FLUENT基础知识总结Fluent是一种专业的计算流体动力学软件,广泛应用于工程领域,用于模拟流体动力学问题。
下面是关于Fluent软件的基础知识总结。
1. Fluent软件概述:Fluent是一种基于有限体积法的流体动力学软件,可用于模拟和分析包括流体流动、传热、化学反应等在内的多种物理现象。
它提供了强大的求解器和网格生成工具,可处理各种复杂的流体问题。
2.求解器类型:Fluent软件提供了多种类型的求解器,用于求解不同类型的流体动力学问题。
其中包括压力-速度耦合求解器、压力-速度分离求解器、多相流求解器等。
用户可以根据具体的问题选择合适的求解器进行模拟计算。
3.网格生成:网格生成是流体模拟中的重要一步,它将复杂的物理几何体离散化成小的几何单元,用于计算流体动力学的变量。
Fluent提供了丰富的网格生成工具,包括结构化网格和非结构化网格。
用户可以通过手动创建网格或使用自动网格生成工具来生成合适的网格。
4.区域设置:在使用Fluent进行模拟计算之前,需要对模拟区域进行设置。
区域设置包括定义物理边界条件、初始化流场参数、设定物理模型参数等。
这些设置将直接影响到最终的模拟结果,因此需要仔细调整和验证。
5.模拟计算过程:模拟计算的过程主要包括输入网格、设置求解器和边界条件、迭代求解控制以及输出结果。
在模拟过程中,用户可以根据需要对物理模型参数、网格精度等进行调整,以获得准确的计算结果。
6.模型与边界条件:Fluent提供了多种物理模型和边界条件设置,包括连续介质模型、湍流模型、辐射模型、化学反应模型等。
用户可以根据具体问题选择合适的模型和边界条件,并根据需要进行参数调整。
7.结果分析:模拟计算结束后,用户可以对计算结果进行分析和后处理。
Fluent提供了丰富的后处理工具,可以对流动场、温度场、压力场等进行可视化展示、数据提取和统计分析。
这有助于用户深入理解流体动力学问题并作出合理的决策。
8.并发计算:Fluent支持并发计算,即使用多台计算机进行模拟计算,以提高计算速度和效率。

fluent流体仿真实例Fluent是一种流体仿真软件,它广泛用于研究和优化各种流体系统。
本文将介绍Fluent的基本工作原理,并以一个实例为例说明如何使用Fluent进行流体仿真。
首先,Fluent采用有限体积法来解决流体问题。
这种方法将流体域划分为许多小的控制体积,并在每个体积中计算流体的平均速度、压力和温度。
然后,通过在体积之间应用质量和动量守恒方程以及其他物理方程来求解流体行为。
最后,Fluent通过计算流场中的速度、压力和温度分布来描绘流体的行为。
为了演示Fluent的用途,我们将以水的流动为例说明如何使用它进行流体仿真。
我们考虑一个具有弯曲管道的水流系统。
假设管道入口处是一个稳定的水流,出口处是一个自由表面,即水流向大气中自由流动。
我们想研究如何通过改变管道形状和入口速度来优化整个系统。
首先,我们需要使用CAD软件绘制出整个系统的几何形状,并将其导入到Fluent中。
然后,我们需要定义出入口处的水流速度和出口处自由表面的边界条件。
这些边界条件将告诉Fluent在哪里应该施加水流速度和处理自由表面的行为。
接下来,我们需要在Fluent中定义数值方法和物理模型。
对于数值方法,我们可以选择不同的离散化方法和求解器,以达到速度和精度的平衡。
对于物理模型,我们需要考虑水的流动特性,包括湍流、速度分布、压力分布等。
这将有助于我们更准确地预测水流的行为,并优化我们的设计。
最后,我们可以开始运行Fluent并分析结果。
Fluent将生成一个包括速度、压力和温度分布的二维或三维图像。
我们可以通过这些图像来研究水流的行为,并探索如何通过改变管道形状和入口速度来优化整个系统。
例如,我们可以通过改变管道半径和斜率来优化水流速度和压力分布。
总之,Fluent是一种广泛使用的流体仿真软件,它可以帮助我们更好地理解和优化各种流体系统。
通过使用Fluent,我们可以确定管道的最佳形状和入口速度,以确保流体系统的最佳性能。

fluent vof模型原理Fluent是一款广泛用于流体动力学仿真计算的软件,具有强大的物理模型和灵活的求解算法。
其中,VOF(VolumeofFluid)模型是Fluent软件中一种重要的流体分离流动模型,主要用于解决两相流体混合问题。
本文将详细介绍VOF模型的基本原理和求解方法。
一、基本原理VOF模型的核心思想是将流场中的流体划分为若干个体积元,并使用一定的标志函数来判断每个体积元是否为特定的流体相。
通过求解标志函数的演化方程,可以获得流场中各相的流动情况。
该模型的关键在于正确设置标志函数和合理选择流体之间的交界面处理方法。
在VOF模型中,通常采用多种流体交界面处理方法,如“软接触”和“硬接触”等。
软接触方法能够较好地处理交界面上的物理和化学反应,适用于复杂的流场和多相流问题;而硬接触方法则更加简单易行,适用于简单的流场和流体流动规律已知的情况。
二、求解方法求解VOF模型通常采用有限体积法,这是一种适用于求解偏微分方程组的数值方法。
在有限体积法中,将计算区域划分为一系列小立方体(称为网格单元),并选择合适的中心点作为隐式方程组的近似解。
对于每个网格单元,根据守恒定律和物理模型的特点,可以建立一系列微分方程和代数方程,并通过求解这些方程来获得流场中各相的密度、速度和温度等参数。
三、应用场景VOF模型广泛应用于航空航天、石油化工、汽车制造等领域中的流体混合问题。
例如,在飞机发动机燃油喷嘴的设计中,需要通过VOF模型模拟燃油与空气的混合过程,以确保燃烧效率;在石油化工领域中,可以通过VOF模型模拟油水混合物在不同条件下的流动和分离过程;在汽车制造领域中,可以通过VOF模型模拟汽车冷却液与空气的混合过程,以提高冷却效果。
四、总结本文详细介绍了Fluent软件中的VOF模型原理和求解方法。
VOF 模型是一种解决流体混合问题的有效工具,能够准确地模拟两相流体的流动和混合过程。
在实际应用中,需要根据具体情况选择合适的交界面处理方法和湍流模型,以确保仿真结果的准确性和可靠性。

CFD软件的对比1、fluent 2006完成被ansys收购!美国,有限体积法FVM法,Fluent已经开发的产品如下:广泛应用!支持c\c++语言开发。
FLUENT6.2---基于非结构化网格的通用CFD求解器,以前的是结构网格求解器,如4.5、5.5版的;Fluent的软件设计基于CFD软件群的思想,从用户需求角度出发,针对各种复杂流动的物理现象,FLUENT软件采用不同的离散格式和数值方法,以期在特定的领域内使计算速度、稳定性和精度等方面达到最佳组合,从而高效率地解决各个领域的复杂流动计算问题。
基于上述思想,Fluent开发了适用于各个领域的流动模拟软件,这些软件能够模拟流体流动、传热传质、化学反应和其它复杂的物理现象,软件之间采用了统一的网格生成技术及共同的图形界面,而各软件之间的区别仅在于应用的工业背景不同,因此大大方便了用户。
GAMBIT——专用的CFD前置处理器(几何/网格生成),FLUENT系列产品皆采用FLUENT 公司自行研发的Gambit前处理软件来建立几何形状及生成网格,是一具有超强组合建构模型能力之前处理器,然后由Fluent进行求解。
Fidap——基于有限元方法的通用CFD求解器,为一专门解决科学及工程上有关流体力学传质及传热等问题的分析软件,是全球第一套使用有限元法于CFD领域的软件,其应用的范围有一般流体的流场、自由表面的问题、紊流、非牛顿流流场、热传、化学反应等等。
FIDAP 本身含有完整的前后处理系统及流场数值分析系统。
对问题整个研究的程序,数据输入与输出的协调及应用均极有效率。
Polyflow——针对粘弹性流动的专用CFD求解器,用有限元法仿真聚合物加工的CFD软件,主要应用于塑料射出成形机,挤型机和吹瓶机的模具设计。
Mixsim——针对搅拌混合问题的专用CFD软件,是一个专业化的前处理器,可建立搅拌槽及混合槽的几何模型,不需要一般计算流力软件的冗长学习过程。

FLUENT算法的一些说明FLUENT算法是一种用于求解流体力学问题的计算流体力学(CFD)软件中的常用算法。
它是通过数值模拟来解决复杂流体流动和传热问题的一种方法。
FLUENT算法的核心是Navier-Stokes方程的离散化求解,能够模拟液体和气体的流动行为。
1.高精度的离散化方法:FLUENT算法采用有限体积法(FVM)进行离散化求解。
有限体积法基于物理量在控制体上的平均值,通过对控制体上的守恒定律进行积分,将控制体内外的通量与体积耦合起来。
这种方法能较好地保持计算量的守恒性和耗散性,适用于复杂流动情况的求解。
2.多种物理模型:FLUENT算法提供了多种物理模型,可用于模拟不同流动和传热问题。
例如,它支持可压缩流动、非定常流动、湍流流动、多相流动、多组分流动、多场耦合问题等。
用户可以根据具体问题选择适当的物理模型。
3. 高效的求解器:FLUENT算法采用了一系列高效的求解器来求解Navier-Stokes方程。
它使用迭代算法进行求解,支持稀疏矩阵的存储和处理,针对不同的问题类型使用合适的求解策略。
此外,FLUENT还支持并行计算,可以将计算任务分配给多个处理器或计算节点,加快求解速度。
4.先进的网格生成:FLUENT算法使用一种自适应网格生成技术,能够根据流动特性和几何形状进行自动的网格划分。
它提供了多种网格生成方法,包括结构网格和非结构网格,并支持网格剖分和网格重构。
这些功能可帮助用户准确地建立模型,提高模拟结果的准确性。
5.丰富的后处理功能:FLUENT算法提供了丰富的后处理功能,可以对求解结果进行可视化和分析。
它支持流场和温度场的可视化显示,可以生成流线、等值面、剖面图等多种图形。
此外,还可以输出各种物理量的曲线和统计数据,帮助用户深入分析模拟结果。
尽管FLUENT算法有许多优点,但在应用过程中也存在一些限制和注意事项。
首先,FLUENT算法对计算资源要求较高,求解过程通常需要大量的计算时间和内存。

fluent计算流体力学(原创版)目录1.Fluent 软件介绍2.Fluent 计算流体力学的原理3.Fluent 在计算流体力学中的应用实例4.Fluent 计算流体力学的优势和局限性5.结论正文一、Fluent 软件介绍Fluent 是一款由美国 CFD 公司(Computational Fluid Dynamics)开发的计算流体力学(Computational Fluid Dynamics,简称 CFD)软件。
该软件广泛应用于工程领域,如航空航天、汽车制造、能源生产等,以模拟和分析流体流动现象。
Fluent 通过计算机模拟流体的运动,可以预测流体在不同条件下的行为,为用户提供优化设计的依据。
二、Fluent 计算流体力学的原理Fluent 基于计算流体力学的原理,采用有限体积法(Finite Volume Method,简称 FVM)对流体进行离散化处理。
在 Fluent 中,流体被划分为无数个小的体积单元,通过对每个体积单元内的流体物理量(如速度、压力、密度等)进行积分,可以得到整个流体的运动状态。
这样的计算方法可以克服传统计算流体力学中的复杂数学方程,使问题变得易于求解。
三、Fluent 在计算流体力学中的应用实例Fluent 在计算流体力学中有广泛的应用,以下是几个具体的实例:1.飞机翼型优化:Fluent 可以用于分析飞机翼型在不同速度下的气流分布,为飞机设计师提供优化设计的依据。
2.汽车尾气排放:Fluent 可以模拟汽车尾气的流动过程,帮助汽车制造商优化排气系统,降低尾气排放。
3.热交换器设计:Fluent 可以分析热交换器内流体的流动状态,为工程师提供优化热交换器性能的建议。
四、Fluent 计算流体力学的优势和局限性1.优势:Fluent 具有强大的计算能力,可以模拟复杂的流体流动现象;计算速度快,效率高;用户界面友好,操作简便。
2.局限性:Fluent 作为一种计算流体力学软件,无法完全替代实验研究;模拟结果受输入参数和模型的限制,可能与实际结果存在一定误差;对计算机硬件要求较高。

Fluent性能分析仅仅就我接触过得谈谈对fluent的认识,并说说哪些用户适合用,哪些不适合fluent对我来说最麻烦的不在里面的设置,因为我本身解决的就是高速流动可压缩N-S方程,而且本人也是学力学的,诸如边界条件设置等概念还是非常清楚的同时我接触的流场模拟,都不会有很特别的介质,所以设置起来很简单对我来说,颇费周折的是gambit做图和生成网格,并不是我不会,而是gambit对作图要求的条件很苛刻,也就是说,稍有不甚,就前功尽弃,当然对于计算流场很简单的用户,这不是问题。
有时候好几天生成不了的图形,突然就搞定了,逐渐我也总结了一点经验,就是要注意一些小的拐角地方的图形,有时候做布尔运算在图形吻合的地方,容易产生一些小的面最终将导致无法在此生成网格,fluent里面的计算方法是有限体积法,而且我觉得它在计算过程中为了加快收敛速度,采取了交错网格,这样,计算精度就不会很高。
同时由于非结构网格,肯定会导致计算精度的下降,所以我一贯来认为在fluent里面选取复杂的粘性模型和高精度的格式没有任何意义,除非你的网格做的非常好。
而且fluent5.5以前的版本(包括5。
5),其物理模型,(比如粘性流体的几个模型)都是预先设定的,所以,对于那些做探索性或者检验新方法而进行的模拟,就不适合用。
同时gambit做网格,对于粘性流体,特别是计算湍流尺度,或者做热流计算来说其网格精度一般是不可能满足的,除非是很小的计算区域所以,用fluent做的比较复杂一点的流场(除了经典的几个基本流场)其计算所得热流,湍流,以及用雷诺应力模拟的粘性都不可能是准确的,这在物理上和计算方法已经给fluent判了死刑,有时候看到很多这样讨论的文章,觉得大家应该从物理和力学的本质上考虑问题。
但是,fluent往往能计算出量级差不多的结果,我曾经做了一个复杂的飞行器热流计算,高超音速流场,得到的壁面热流,居然在量级上是吻合的,但是,从计算热流需要的壁面网格精度来判断,gambit所做的网格比起壁面网格所满足的尺寸的要大了至少2个数量级,我到现在还不明白fluent是怎么搞的。
FLUENT中的求解器算法和离散方法首先,FLUENT使用的求解器是基于有限体积法的。
有限体积法将流体域划分为很多离散的体积单元,然后通过求解每个体积单元上的守恒方程来获得流体的数值解。
常用的有限体积法求解器包括显式求解器和隐式求解器。
FLUENT中使用的是隐式求解器,具有更好的稳定性和数值精度。
在FLUENT中,液体和气体的流动是通过流体动力学方程来描述的。
对于不可压缩流体,使用Navier-Stokes方程来描述,而对于可压缩流体,使用RANS(雷诺平均纳维尔-斯托克斯)方程来描述。
FLUENT中的求解器采用迭代方法,通过不断迭代更新流场解,直到收敛为止。
对于离散方法,FLUENT中使用的是有限体积法。
在有限体积法中,流体域被划分为很多离散的体积单元。
对每个体积单元,守恒方程被积分,并转化为离散的形式。
然后,根据边界条件和数值格式,得到一个线性或非线性的代数方程组。
这个方程组可以通过迭代求解器进行求解,以得到流体的数值解。
在FLUENT中,流场的离散方法包括网格生成、重构和适应。
网格生成是将流体域划分为离散的体积单元的过程。
FLUENT提供了多种网格生成方法,包括结构网格和非结构网格,在不同的流场中有不同的适用性。
网格重构是对现有网格进行优化和改进的过程,以改善数值解的精度和稳定性。
网格适应是根据流场的特点和要求,自适应地调整网格的过程,以提高计算效率和精度。
除了求解器和离散方法,FLUENT还采用了多种数值解算算法来提高求解效率和精度。
例如,FLUENT中使用了几种迭代算法来解决代数方程组,如雅可比迭代、高斯赛德尔迭代和共轭梯度方法。
这些算法根据流场的特点和求解的要求,选择最合适的迭代方法,以加快求解速度和提高求解精度。
总之,FLUENT中的求解器、算法和离散方法是通过有限体积法来模拟和解决流体流动问题的。
它使用了隐式求解器、网格生成、重构和适应等离散方法,以及迭代算法和数值解算算法来求解流体动力学方程。
fluent求解方程Fluent是一种流体力学仿真软件,它可以用来求解各种复杂的方程。
本文将以Fluent求解方程为主题,介绍Fluent的基本原理、使用方法以及一些应用案例。
我们来了解一下Fluent的基本原理。
Fluent是基于有限体积法的流体力学仿真软件,它可以对流体的流动、传热、传质以及化学反应等问题进行模拟和求解。
有限体积法是一种将连续介质分割成有限体积单元的方法,通过对每个体积单元进行离散,建立方程组,并采用数值方法求解这些方程组,从而得到流体的各种物理量。
在Fluent中,我们可以通过建立几何模型、设定边界条件和物理参数等步骤来进行仿真计算。
首先,我们需要根据实际情况建立几何模型,可以通过绘制几何图形、导入CAD文件或者使用预定义的几何模板来完成。
然后,我们需要设定边界条件,例如流体的入口速度、出口压力、壁面温度等。
同时,我们还需要指定流体的物理性质,如密度、粘度、热传导系数等。
最后,我们可以选择合适的求解器和求解方法,并设置收敛准则和计算参数,然后启动求解器开始计算。
Fluent可以求解的方程非常广泛,包括流体动力学方程、传热方程、质量传递方程、化学反应方程等。
在流体动力学方程中,我们可以求解连续方程、动量方程和能量方程,从而得到流体的速度、压力和温度分布。
在传热方程中,我们可以求解热传导方程和对流传热方程,从而得到流体的温度分布和热传输情况。
在质量传递方程中,我们可以求解质量守恒方程和物质传输方程,从而得到物质的浓度分布和传输情况。
在化学反应方程中,我们可以求解反应动力学方程和质量守恒方程,从而得到反应物的浓度和反应速率。
Fluent的应用非常广泛,可以用于汽车、航空航天、能源、化工、环境保护等领域的研究和设计。
例如,在汽车工程中,可以使用Fluent对车辆的空气动力学性能进行仿真计算,从而优化车身外形和空气动力学布局,提高车辆的燃油经济性和稳定性。
在航空航天工程中,可以使用Fluent对飞机的气动性能进行仿真计算,优化飞机的机翼、机身和尾翼等部件的设计,提高飞机的升力和降阻。
fluent流体仿真软件原理
Fluent流体仿真软件是由美国Ansys公司开发的一款流体动力
学仿真软件,它基于有限体积法和数值求解方法,用于模拟和分析
流体力学现象。
其原理涉及以下几个方面:
1. 有限体积法,Fluent使用有限体积法对流场进行离散化处理。
它将流场分割成有限体积的控制体,并在每个控制体内求解流
体的守恒方程,如质量守恒、动量守恒和能量守恒等。
这种方法能
够准确描述流体在空间和时间上的变化,是流体动力学仿真的基础。
2. 数值求解方法,Fluent采用数值求解方法对离散化后的守
恒方程进行求解。
这包括对流方程、扩散方程和源项的离散化处理,以及时间推进和迭代求解等过程。
通过数值求解方法,可以得到流
场的速度、压力、温度等物理量的分布和变化规律。
3. 物理模型,Fluent软件内置了多种物理模型,包括湍流模型、传热模型、化学反应模型等,用于描述不同流体现象的特性。
用户可以根据具体问题选择合适的物理模型,对流场进行更精确的
仿真和分析。
4. 网格生成,在进行流体仿真前,需要对计算区域进行网格划分。
Fluent能够生成结构化或非结构化网格,以适应不同流场的复杂几何形状和流动特性。
良好的网格质量对于准确求解流场至关重要。
总的来说,Fluent流体仿真软件的原理包括有限体积法的离散化处理、数值求解方法的应用、物理模型的选择和网格生成等多个方面。
通过这些原理的综合运用,Fluent能够对流体力学现象进行准确、高效的模拟和分析,为工程和科研领域提供重要的支持和帮助。
FLUENT中各种算法的差别
1.网格独立算法:网格独立算法是FLUENT中最常用的算法,它是一
种基于方程和计算网格的数值解法。
它以多步积分的形式将求解的流体动
力学方程分解为一系列可处理的数值解的子步骤,以生成满足流体力学方
程和网格的精确解。
它可以处理几何变形、边界条件的变化、非稳态流体
问题和多场耦合等问题。
2.有限体积法:有限体积法(FV)是一种常用的求解偏微分方程的技术,它将流体力学方程分解为一系列无参考的计算步骤,从而求解数值解。
FLUENT中的有限体积算法采用变分法对求解的核心微分方程进行离散,
无需考虑算法的收敛性,可以轻松处理复杂的流动场景,以及要求高精度
的问题。
3.增量方法:自从增量方法(DA)诞生以来,一直都是解决复杂流体
力学问题的有力工具。
类似网格独立算法,它分解问题并生成一系列数值解。
但是,增量方法允许使用更小的求解步骤来计算更高精度的解,从而
更为有效地产生流体力学解决方案。
1.非耦合求解(Segregated);2.耦合隐式求解(Coupled Implicit);3.耦合显式求解(Coupled Explicit) 非耦合求解方法主要用于不可压缩或压缩性不强的流体流动。
耦合求解则可以用在高速可压缩流动。
FLUENT默认设置是非耦合求解,但对于高速可压流动,有强的体积力(浮力或离心力)的流动,求解问题时网格要比较密,建议采用耦合隐式求解方法,可以耦合求解能量和动量方程,能比较快地得到收敛解。
缺点是需要的内存比较大(是非耦合求解迭代时间的1.5-2倍)。
如果必须要耦合求解,但是你的机器内存不够,这时候可以考虑用耦合显式解法器求解问题。
该解法器也耦合了动量,能量及组分方程,但内存却比隐式求解方法小。
缺点是收敛时间比较长。
这里需要指出的是非耦合求解的一些模型在耦合求解解法器里并不都有。
耦合解法器没有的模型包括:多相流模型,混合分数/PDF燃烧模型,预混燃烧模型,污染物生成模型,相变模型,Rosseland辐射模型,确定质量流率的周期性流动模型及周期性换热模型等。
隐式(Implicit):对于给定变量,单元内的未知值用邻近单元的已知和未知值计算得出。
因此,每一个未知值会在不止一个方程中出现,这些方程必须同时解来给出未知量。
显式(Explicit):对于给定变量,每一个单元内的未知量用只包含已知量的关系式计算得到。
因此未知量只在一个方程中出现,而且每一个单元内的未知量的方程只需解一次就可以给出未知量的值。
一阶迎风格式(First Order Upwind):当需要一阶精度时,我们假定描述单元内变量平均值的单元中心变量就是整个单元内各个变量的值,而且单元表面的量等于单元内的量。
因此,当选择一阶迎风格式时,表面值被设定等于迎风单元的单元中心值。
二阶迎风格式(Second Order Upwind):当需要二阶精度时,使用多维线性重建方法来计算单元表面处的值。
在这种方法中,通过单元中心解在单元中心处的泰勒展开来实现单元表面的二阶精度值。
第4章 有限体积法
1.1 积分方程
守恒方程的形式为积分方程。
⎰⎰⎰+⋅=⋅Ω
S
S
Ωq S ΓS d d grad d φφρφn n v ( 4-1 )
4.1 控制体积
求解区域用网格分割有限个控制体积(Control V olumes, CVs )。
同有限差分不同的是,网格为控制体积的边界,而不是计算节点。
为了保证守恒,CVs 必须是不重叠的,且表面同相邻CVs 是同一个。
i.
节点为中心
CVs 的节点在控制体积的中心。
先定义网格,任何找出中心点。
优点:节点值代表CVs 的平均值,可达二阶精度。
ii.
界面为中心
CVs 的边界线在节点间中心线上。
先定义节点,再划分网格。
优点:CV 表面上的CDS 差分精度比上面方法高。
两个方法基本一样,但在积分时要考虑到位置。
但第一个方法用得比较多。
节点为中心 界面为中心
∑⎰⎰
=k
S S
k
fdS fdS ( 4-2 )
- 对流:n v ⋅=ρφf 在垂直于界面的方向 - 扩散:n ⋅=φgrad Γf 在垂直于界面的方向 如果速度也是未知的,则要结合其它方程一起求解。
考虑界面e ,通过表面的总通量为: 1. 基于界面中心值
中间点定理:(midpoint rule) 表面积分为格子表面上的中心点的值和表面积的乘积。
e
e e S e e S
f S f fdS F e
≈==⎰ ( 4-3 )
此近似为2阶精度。
由于f 在格子界面没有定义值,它必须通过插值来得到。
为了保证原有的2阶精度,插值方法也须采用2阶精度的方法。
2. 基于界面顶角值
当已定义角上的值时,2阶精度的方法还有:
()⎰+=
=e
S se ne e
e f f S fdS F 2 ( 4-4 )
3. 高阶精度近似
()⎰++=
=e
S se e ne e
e f f f S fdS F 46
( 4-5 ) 4阶精度Simpson 法。
4.3 体积积分近似
⎰∆≈∆==Ω
P P Ωq Ωq qd ΩQ ( 4-6 )
q p 为CV 中心节点值。
高阶精度要求为节点的插值或形状函数来表示。
如
),(),(y x f y x q =。
然后对体积积分。
4.4 插值方法
4.4.1 上风插值格式(UDS )
φe 用e 上游(upstream )上的值,通过1阶向前差分或向后差分来表示。
⎩⎨⎧<⋅>⋅=0
)(;0)(e w
e P
P n v if
n v if φφφ ( 4-7 )
此方法为唯一的无条件满足边界准则的近似,即不产生振荡解。
但它的数值扩散效应很大。
从Taylor 展开:
()()H x x x x x x P
P e
P
P e P e +⎪⎪⎭⎫
⎝⎛∂∂-+⎪⎭⎫
⎝⎛∂∂-+=222
2φφφφ ( 4-8 ) 它取得的是第一项,因此,精度是1阶的。
它的截断误差为扩散项。
即
e
e d e x
f ⎪⎭⎫
⎝⎛∂∂Γ=φ ( 4-9 )
此系数为数值的,人工的,伪的。
()2/x u e num e ∆=Γρ ( 4-10 )
此扩散产生在垂直于流动方向或在流线方向。
为特别严重的误差。
尤其对于有峰值或有较大变化的变量,会使值光滑,要得到精确的解,需要很精细的网格。
4.4.2
线性插值格式(CDS )
()e P e E e λφλφφ-+=1 ( 4-11 )
λ 为线性插值因子。
定义为:
,P
E P
e e x x x x --=
λ ( 4-12 )
用Tayler 展开可得到此方法的截断误差:
()()()H x x x x x P
e E P e e P e E e +⎪
⎪⎭⎫
⎝⎛∂∂----+=222
1φλφλφφ ( 4-13 )
为2阶精度。
和其它所有高精度一样,会发生数值振荡。
假定线性分布,则在e 点的导数可以表示成:
P
E P E
e x x x --≈⎪⎭⎫
⎝⎛∂∂φφφ ( 4-14 ) 如e 在两点的中央时,为2阶精度。
4.4.3
二次迎风插值(QUICK )格式
Quadratic Upwind Interpolation for Convective Kinematics
用抛物线(2次)分布代替线性(1次)分布。
抛物线需要3点。
这第3点取在上风点上。
对于E 点,当u>0,取W ,当u<0时取EE 点。
()()⎩⎨
⎧<+-+->+-+-=;
01;0143432121x E EE P x P W E e u for g g g g u for g g g g φφφφφφφ ( 4-15 )
其中,g 可以表示成用插值系数来表示:
()()()()()
;
1;111;
111;12,,2
,,4,,2,,3,,2
,,2
,,2,,1
P
e E e E
e P e P
e E e P
e W
e W
e P e W
e P
e W
e P e P
e W e g g g g λλλ
λλλλλλλλλλλλλ-+=
-+-+=
-+--=
-+-=
( 4-16 )
对于均匀网格:
∙ 3/8: 下游值 ∙ 6/8: 上游值
∙ -1/8:第2个上游点
此方法为3阶精度截断误差。
因均匀网格的Taylor 展开可以表示成:
()()w p E P E P
W E P e H x x φφφφφφφφφφ+--+=+⎪⎪⎭⎫
⎝⎛∂∂∆--+=28
1
2;483818386333
( 4-17 )
此方法的缺点是多了一个点,且非均匀网格的系数复杂。
但是,当此方法用于中间点法则近似时,面积分仍是2阶精度。
虽然此时QUICK 方法比CDS 方法稍微精确一点,但二个方法都在2阶方法上渐近收敛,相差不大。
4.4.4
高精度格式
用高阶代数式表示:如
332210)(x a x a x a a x +++=φ ( 4-18 )
4.4.5
其它格式
∙ 线性上风格式(LUDS ):使用上游2点的线性外推; ∙ 斜迎风格式(skew upwind scheme ):沿流线使用上游2点的线性外推; ∙
混合格式:Spalding 的根据Peclet 数对UDS(Pe>2)和CDS(Pe ≤2)的选择
4.5 边界条件的使用
每个CV 提供一个代数方程。
但是对于在边界上的格子,表面通量要另行处理。
表面通量要求已知,或与内部和边界上的值的关系已知。
也许不一定要引进其它附加的未知数。
由于在区域外已无节点,这些近似因基于单边的差分或外推。
4.5.1
对流通量
∙ 流入(inflow )边界:对流通量; ∙ 无穿透壁面和对称平面上:零通量。
∙
流出(outflow )边界:垂直此方向的通量是独立的。
此时,使用上游值。
4.5.2
扩散通量
∙
壁面:有时定义,如壁面热流密度。
使用单边近似方法 在已知通量的条件下,则可用于计算边界的值。
4.6 代数方程系统
同差分方法一样。
4.7 例子
4.7.1 传输方程
⎰⎰⋅Γ=⋅S
S
S n S d grad d φρφn v ( 4-19 )
边界条件:
对流项: for face e:
⎰⋅=e
S c e S F d n v ρφ ( 4-20 )
()y u dS m
e x S e e
∆=⋅=⎰ρρn v ( 4-21 )
()⎩⎨
⎧+-+=CDS for m m UDS for m m
F E
e e P e e E e P e c e φλφλφφ)1()0,min(0,max ( 4-22 )
λ为线性插值系数。
UDS:
)
();0,min();0,min();0,min();0,min(c
S c N c W c E c P s c
S n c
N w c
W e c E A A A A A m
A m
A m A m A +++-===== ( 4-23 ) CDS:
)
(;;;;c
S c N c W c E c P n n c
N n n c
N w w c
W e e c
E A A A A A m
A m
A m A m
A +++-=====λλλλ ( 4-24 )
连续性条件
0=+++s n w e m m m m
( 4-25 )。