椭圆柱形储油罐剩余油量的计算

【下载本文档，可以自由复制内容或自由编辑修改内容，更多精彩文章，期待你的好评和关注，我将一如既往为您服务】储罐油量计算方法1 油品算量操作1.1 术语和定义（国标GB/T 19779-2005） 1.1.1 游离水（FW ）在油品中独立分层并主要存在于油品下面的水。

FW V 表示游离水的扣除量，其中包括底部沉淀物。

1.1.2 沉淀物和水（SW ）油品中的悬浮沉淀物、溶解水和悬浮水总称为沉淀物和水。

其质量分数或体积分数、体积和质量分别用SW %、SW V 和SW m 表示。

1.1.3 沉淀物和水的修正系数（CSW ）为扣除油品中的沉淀物和水（SW ）将毛标准体积修正到净标准体积或将毛质量修正到净质量的修正系数。

1.1.4 体积修正系数（VCF ）将油品从计量温度下的体积修正到标准体积的修正系数。

用标准温度下的体积与其在非标准温度下的体积之比表示。

等同于液体温度修正系数（CTL ） 1.1.5 罐壁温度修正系数（CTSh ）将油罐从标准温度下的标定容积（即油罐容积表示值）修正到使用温度下实际容积的修正系数。

1.1.6 总计量体积（to V ）在计量温度下，所有油品、沉淀物和水以及游离水的总测量体积。

1.1.7 毛计量体积（go V ）在计量温度下，已扣除游离水的所有油品以及沉淀物和水的总测量体积。

1.1.8 毛标准体积（gs V ）在标准温度下，已扣除游离水的所有油品及沉淀物和水的总体积。

通过计量温度和标准密度所对应的体积修正系数修正毛计量体积可得到毛标准体积。

1.1.9 净标准体积（ns V ）在标准温度下，已扣除游离水及沉淀物和水的所有油品的总体积。

从毛标准体积中扣除沉淀物和水可得到净标准体积。

1.1.10 表观质量（m ）有别于未进行空气浮力影响修正的真空中的质量，表观质量是油品在空气中称重所获得的数值，也习惯称为商业质量或重量。

通过空气浮力影响的修正也可以由油品体积计算出油品在空气中的表观质量。

一种椭圆型储油罐纵向倾斜的变位识别模型摘要：本文给出了一种椭圆型储油罐罐体发生纵向倾斜变位后对罐容表进行重新标定的数学模型。

本文首先利用微积分中的微元法，确定了椭圆油罐未变位和变位两种情况下储油量与其油位高度的关系式，进而可利用matlab软件确定椭圆储油罐无变位和变位两种情况下的待定系数，并可将所得模型与无变位和倾斜角为a=4.10时的纵向变位两种实验情况的具体数据所得图像进行比较，对产生的误差进行分析。

关键词：储油罐纵向倾斜变位识别模型微元法积分引言加油站储油罐配套的”油位计量管理系统”是利用流量计和油位计测量进/出油量与罐内油位高度等数据通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。

但是，在实际生活中储油罐使用一段时间后，罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变。

所以需要定期对罐容表进行重新标定。

为了解决实际储油罐的变位与罐容表标定的问题，利用2010年全国大学生数学建模竞赛a题提供的椭圆型罐体纵向倾斜变位对罐容表的影响的数据，对该形状罐体无变位和倾斜角为a=4.10的纵向变位两种情况进行分析，利用积分方法建立了油位高度与体积之间的关系，并用matlab对数据分析得到待定常数的取值，从而最终得出椭圆型罐体纵向倾斜变位后对罐容表的影响模型。

一、问题分析首先，对问题进行定性分析。

考虑到当油罐只发生纵向倾斜时，测位浮标所在的纵向切面的面积不变。

由此，可以将倾斜后的高度h与倾斜前的高度h0联系起来。

而未倾斜时的高度h0又能够关联油罐内油的体积，所以就能建立h与体积v，倾斜角度?%z之间的数学模型。

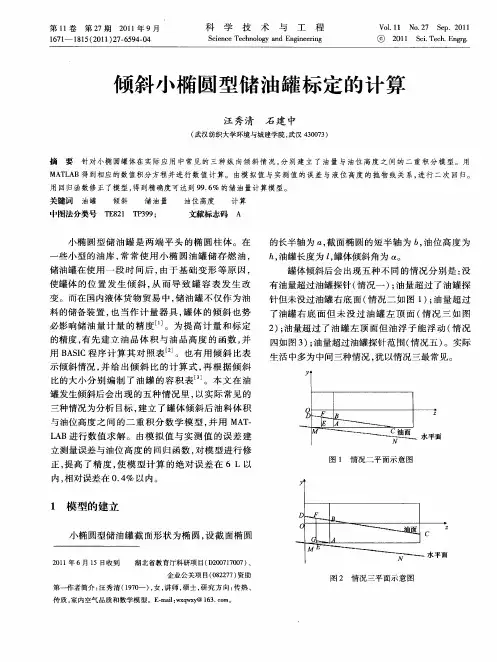
二、模型求解与建立1.建立油罐变位前后液面高度间的关系假设油罐成椭圆平底型，则浮标所在的纵向切面为矩形（如图1），设油罐发生倾斜时液面线与未偏移时液面线的交点到左侧面距离为x（如图2），因为该切面始终保持面积相等，故有：1/2*x*x*tan(a)= 1/2*(l-x)*(l-x)*tan(a)解之可得：x=1/2l从而可计算出油罐发生倾斜前后液面高度差：△h=(1/2l-m)tan(a)已知浮标测量得到的液面高h，转化为未倾斜时的液面高h0为h0=h-△h=h-(1/2l-m)tan(a)3.确定积分常数使用matlab对实验数据进行拟合，可得拟合多项式函数关系，计算v(0)的值，代入上述模型v0，可计算得c，从而得到油罐未倾斜和倾斜时体积与浮标所示油面高度之间的关系模型。

储罐油量计算方法1 油品算量操作1.1 术语和定义（国标GB/T 19779-2005） 1.1.1 游离水（FW ）在油品中独立分层并主要存在于油品下面的水。

FW V 表示游离水的扣除量，其中包括底部沉淀物。

1.1.2 沉淀物和水（SW ）油品中的悬浮沉淀物、溶解水和悬浮水总称为沉淀物和水。

其质量分数或体积分数、体积和质量分别用SW %、SW V 和SW m 表示。

1.1.3 沉淀物和水的修正系数（CSW ）为扣除油品中的沉淀物和水（SW ）将毛标准体积修正到净标准体积或将毛质量修正到净质量的修正系数。

1.1.4 体积修正系数（VCF ）将油品从计量温度下的体积修正到标准体积的修正系数。

用标准温度下的体积与其在非标准温度下的体积之比表示。

等同于液体温度修正系数（CTL ） 1.1.5 罐壁温度修正系数（CTSh ）将油罐从标准温度下的标定容积（即油罐容积表示值）修正到使用温度下实际容积的修正系数。

1.1.6 总计量体积（to V ）在计量温度下，所有油品、沉淀物和水以及游离水的总测量体积。

1.1.7 毛计量体积（go V ）在计量温度下，已扣除游离水的所有油品以及沉淀物和水的总测量体积。

1.1.8 毛标准体积（gs V ）在标准温度下，已扣除游离水的所有油品及沉淀物和水的总体积。

通过计量温度和标准密度所对应的体积修正系数修正毛计量体积可得到毛标准体积。

1.1.9 净标准体积（ns V ）在标准温度下，已扣除游离水及沉淀物和水的所有油品的总体积。

从毛标准体积中扣除沉淀物和水可得到净标准体积。

1.1.10 表观质量（m ）有别于未进行空气浮力影响修正的真空中的质量，表观质量是油品在空气中称重所获得的数值，也习惯称为商业质量或重量。

通过空气浮力影响的修正也可以由油品体积计算出油品在空气中的表观质量。

1.1.11 表观质量换算系数（WCF ）将油品从标准体积换算为空气中的表观质量的系数。

该系数等于标准密度减去空气浮力修正值。

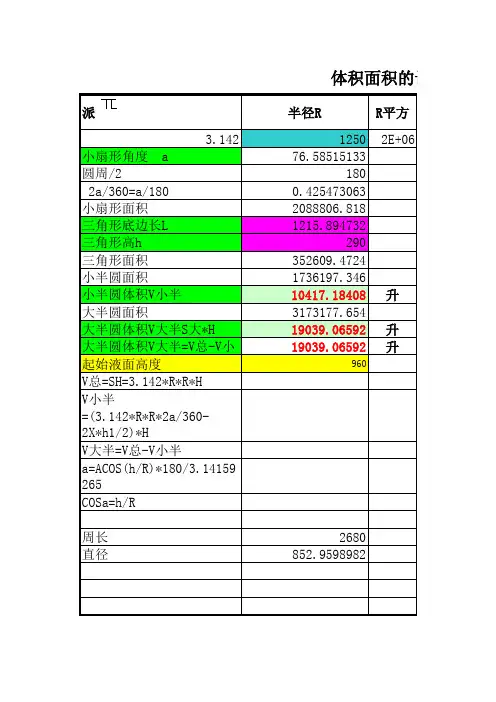
体积面积的计算
派半径R R平方
3.14212502E+06
小扇形角度 a76.58515133
圆周/2180
2a/360=a/1800.425473063
小扇形面积2088806.818
三角形底边长L1215.894732
三角形高h290
三角形面积352609.4724
小半圆面积1736197.346
小半圆体积V小半10417.18408升
大半圆面积3173177.654
大半圆体积V大半S大*H19039.06592升
大半圆体积V大半=V总-V小19039.06592升
起始液面高度960
V总=SH=3.142*R*R*H
V小半=(3.142*R*R*2a/360-2X*h1/2)*H
V大半=V总-V小半
a=ACOS(h/R)*180/3.14159265
COSa=h/R
周长2680
直径852.9598982
总面积S=3.142*R*R
高度H 体积V总=S*H/1000000
4909375600029456.25
的计算公式
注：此计算方式已经过优化修改，附属页属于计算引用表，不可随意篡改，否则计算结果误差会加大，只输入半径、高度、与液面高度即可得出剩余油量如有大的偏差或更好计算方法，请共同交流 \。

各种常见油罐储油量的计算方法摘要：本文介绍了一些常见形状的储油罐油量的计算方法,并给出了每种形状的储油罐容积的计算公式和整个推导过程，供各位同仁共同探讨和分享。

现实生活中，尽管储油罐的形状各式各样,仔细分析无非存在以下两种结构：卧式结构和立式结构。

无论是卧式结构还是立式结构，都有可能存在半椭圆形封头、平面封头、半圆形封头、圆锥形封头等。

笔者在计算储油罐的过程中，积累了大量的经验，现简要做一介绍。

一、椭圆封头卧式椭圆形油罐这种油罐的形状一般是两端封头为半椭球形，中间为截面积是椭圆形的椭圆柱体，如图1—1、图1-2所示.计算时，可以把这种油罐的容积看成两部分，一部分为椭球体（把两端的封头看作是一个椭球)，另一部分为平面封头中间截面为椭圆形的椭圆柱体，见图1-3、图1—4所示，然后，采用微积分计算任一液面高度时油罐内的容积。

我们建立如图1—3、图1—4所示的坐标系,设油罐除封头以外的长度为L ，其截面长半轴为A ，短半轴为B 。

椭球部分的长半轴为B ，短半轴为C,则在图1—3、图1-4所示的坐标系中，分别得到椭圆的方程为： 在某一液面高度H 时,油罐内油的容积为：由（1）得: L C BA y图1-2：椭圆封头卧式椭圆形油罐结构图 图1-1：椭圆封头卧式椭圆形油罐实体图 H(0,2b)a Δy - a (0,b) 0x y 图1-3：椭圆柱体剖面图 L H(0,2b)CΔy- C (0,b) 0 z 图1-4：封头椭球体剖面图 dyxz xL 2V H⎰π+=）（2y By 2BAx -=C（3） （4）⎰⎰π+=H 0Hxzdyxdy L 21B B y A x 2222=-+）（（1） （2） 1C z B B y 2222=+-）（由(2）得： 将（4）、（5)代入（3)得：公式（6）即为任意截面高度时油罐中油的容积。

若用余旋计算,还可以得到如下的公式：二、平面封头卧式椭圆形油罐这种油罐的形状一般两端为平面封头,中间截面积为椭圆形的椭圆柱体,如图2—1、图2—2所示.这种油罐任一液面高度时，油罐内油的容积的计算公式可以参照上述方法推导，但要比椭圆封头卧式椭圆形的油罐简单的多。

excel油罐剩余油量计算公式
在Excel中，可以使用简单的数学公式来计算油罐的剩余油量。

假设你有一个单元格包含油罐的总容量，另一个单元格包含当前油
罐中的油量。

你可以使用以下公式来计算剩余油量：
剩余油量 = 总容量当前油量。

假设总容量的单元格是A1，当前油量的单元格是B1，那么公式
将是：
=C1-B1。

这将在C1中显示剩余油量。

请确保使用正确的单位，例如升或
加仑，以便公式计算正确。

另外，你也可以考虑将单位转换为统一
的单位后再进行计算。

如果你有多个油罐需要计算，可以将上述公式应用到每个油罐
的相应单元格中，以便快速计算出剩余油量。

除了基本的减法公式外，你还可以根据需要添加其他因素，比
如温度、压力等，来进行更复杂的油量计算。

这将需要使用更复杂的数学公式和函数，但基本原理仍然是一样的，即将相关因素考虑在内，然后进行计算。

总之，在Excel中计算油罐的剩余油量，你需要考虑油罐的总容量、当前油量以及其他可能影响油量的因素，然后使用合适的数学公式来进行计算。

希望这些信息能够帮助到你。

油罐储油量的校核油罐容积与储油量在设计资料中，立式油罐和卧式油罐均只有最大容积数据，但没有容积与油罐内储油高度的对应关系；因此，油库的储油量经常估算不准，误差很大，不利于锅炉燃油消耗的分析、核算和监督。

为了建立油罐高度与储油量的数学模式，实测了卧式油罐的直径（内径2.52m）、长度、两端球面封头等数据。

同时，查找、核实了立式油罐的设计数据，经过精确、认真地计算（油位精确到0.01m），得到了油罐的高度与储油量的对应数据，并实测了#0轻柴油的密度（~m3），按m3的密度计算，建立了油罐罐容表，经过一个月的实际检验，其误差在%左右。

50m3卧式油罐储油量的计算卧式油罐的储油量与其罐内储油高度的数学关系，是非线性函数。

经查找资料和现场核实，建立了卧式油罐储油量与其油位的数学模式。

该模式同样适用于类似容器容积的计算。

卧式油罐主体简图卧式油罐主体外形见图，已知油罐圆柱体半径为R=1.26m，长度为L1=9.6m，油罐两端凸型封头最大长度均为L2=0.5m；一、油罐圆柱体部分容积V1的计算设油罐圆柱体油面宽度为2B，油面距罐顶高度为H；则油位为：2R－H；油罐横截面积为：m=πR2，设未储油部分的弓形截面积为m1，则储油部分的截面积为S=m－m1；储油体积为：V1=SL11.弓形截面积m1的计算：扇形面积S1=RL/2=θR2/2，而θ=2{(π/2)－ArcSin[(R－H)/R]}故：S1={(π/2)－ArcSin[(R－H)/R]}R2三角面积S2=2B(R－H)/2= B(R－H)由相交弦定律知：B2=H[(R－H) +R]= H(2R－H)得：B=[ H(2R－H)]1/2，则S2=(R－H) [ H(2R－H)]1/2故：m1= S1－S2={(π/2)－ArcSin[(R－H)/R]}R2－(R－H) [ H(2R－H)]1/22.油罐圆柱体部分的储油体积V1=SL1=( m－m1) L1=｛πR2－{(π/2)－ArcSin[(R－H)/R]}R2－(R－H) [ H(2R－H)]1/2｝L1其中，R已知，V1仅与油面距罐顶高度H即变量油位有关。

油罐油的重量计算公式在石油化工行业中，油罐是用来存储原油、燃料油、柴油等石油制品的重要设备。

对于石油化工企业来说，准确计算油罐中石油制品的重量是非常重要的，这不仅关系到企业的生产成本，还关系到产品的质量和安全。

因此，了解油罐油的重量计算公式是非常必要的。

油罐油的重量计算公式可以通过以下步骤来进行计算：第一步，测量油罐的容积。

首先，需要测量油罐的容积。

油罐的容积通常使用立方米（m³）或者立方英尺（ft³）来表示。

测量油罐容积的方法有多种，常用的方法包括使用测量尺、激光测量仪或者超声波测量仪来进行测量。

在测量油罐容积时，需要考虑到油罐的形状和尺寸，以确保测量结果的准确性。

第二步，确定石油制品的密度。

在计算油罐油的重量时，需要确定石油制品的密度。

石油制品的密度是指单位体积内石油制品的质量，通常使用千克/立方米（kg/m³）或者磅/立方英尺（lb/ft³）来表示。

石油制品的密度是根据具体的石油制品种类和成分来确定的，可以通过实验室测试或者查阅相关资料来获取。

第三步，计算油罐油的重量。

一旦确定了油罐的容积和石油制品的密度，就可以使用以下公式来计算油罐油的重量：油罐油的重量 = 油罐容积×石油制品密度。

在计算油罐油的重量时，需要注意单位的统一。

如果油罐容积使用的是立方米，石油制品密度使用的是千克/立方米，则计算结果为千克；如果油罐容积使用的是立方英尺，石油制品密度使用的是磅/立方英尺，则计算结果为磅。

除了上述的基本计算公式外，还需要考虑到油罐内部的温度和压力对石油制品密度的影响。

石油制品的密度会随着温度和压力的变化而发生变化，因此在实际计算中需要对这些因素进行修正。

此外，对于储存不同种类石油制品的油罐，其密度和重量计算公式也会有所不同。

因此，在实际应用中需要根据具体情况进行调整和修正，以确保计算结果的准确性。

总之，油罐油的重量计算公式是石油化工企业生产管理中的重要工具，通过准确计算油罐油的重量，可以帮助企业合理安排生产计划、控制生产成本，确保产品质量和安全生产。