下载文档原格式
多面体与旋转体一、棱柱1、 由几个多边形围成的封闭的几何体叫做多面体。
2、 两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面围成的多面体叫做棱柱。
棱柱的互相平行的两个面叫做棱柱的底面，其余各面叫做棱柱的侧面，相邻的两个侧面的公共边叫做棱柱的侧棱，两个底面间的距离叫做棱柱的高。
棱柱的基本性质：（1） 棱柱的侧面都是平行四边形。
（2） 棱柱的两个底面及平行于底面的截面都是全等的多边形。
3、 侧棱与底面不垂直的的棱柱叫做斜棱柱。
侧棱与底面垂直的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
性质：（1） 直棱柱侧面都是矩形。
（2） 直棱柱侧棱与高相等。
（3） 正棱柱的侧面都是全等的矩形。
4、 底面是平行四边形的棱柱叫做平行六面体。
底面是矩形的直棱柱是长方体。
长方体的对角线平方等于三边长的平方和。
5、 夹在两个平行平面间的两个几何体，如果被平行于这两个平面的任何平面所截得的两个截面的面积都相等，那么这两个几何体的体积相等。
6、 h V S =⋅棱柱底. 二、棱锥1、有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥。
棱锥的这个多边形的面叫做底面，其余各个三角形的面叫做侧面。
相邻的两个侧面的公共边叫做棱锥的侧棱。
各个侧面的公共顶点叫做棱锥的顶点，顶点到底面的距离叫做棱锥的高。
棱锥的基本性质：如果一个棱锥被平行于底面的一个平面所截，那么： （1） 侧棱和高被这个平面分成比例线段； （2） 截面和底面都是相似多边形；（3） 截面面积与底面面积之比，等于顶点到截面与顶点到底面的距离平方之比。
2、如果一个棱锥的底面是正多边形，且顶点在底面的射影是底面的中心，这个棱锥叫做正棱锥。
正棱锥的性质：（1） 各侧棱相等，各侧面都是全等的等腰三角形。
（2） 正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形。
正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
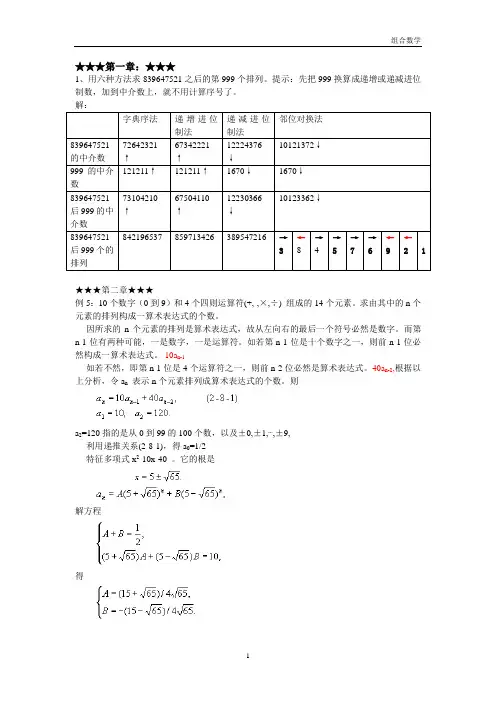
★★★第一章：★★★1、用六种方法求839647521之后的第999个排列。
提示：先把999换算成递增或递减进位制数，加到中介数上，就不用计算序号了。
解：字典序法递增进位制法递减进位制法邻位对换法839647521的中介数72642321↑67342221↑12224376↓10121372↓999的中介数121211↑121211↑1670↓1670↓839647521后999的中介数73104210↑67504110↑12230366↓10123362↓839647521后999个的排列842196537 859713426 389547216 →3←8→4→5→7→6←9←21★★★第二章★★★例5：10个数字（0到9）和4个四则运算符(+,-,×,÷) 组成的14个元素。
求由其中的n个元素的排列构成一算术表达式的个数。
因所求的n个元素的排列是算术表达式，故从左向右的最后一个符号必然是数字。
而第n-1位有两种可能，一是数字，一是运算符。
如若第n-1位是十个数字之一，则前n-1位必然构成一算术表达式。
10a n-1如若不然，即第n-1位是4个运算符之一，则前n-2位必然是算术表达式。
40a n-2,根据以上分析，令a n表示n个元素排列成算术表达式的个数。
则a2=120指的是从0到99的100个数，以及±0,±1,...,±9,利用递推关系(2-8-1)，得a0=1/2特征多项式x2-10x-40 。
它的根是解方程得例7：平面上有一点P，它是n个域D1,D2,...,D n的共同交界点，见图2-8-4现取k种颜色对这n个域进行着色，要求相邻两个域着的颜色不同。
试求着色的方案数。
令a n表示这n个域的着色方案数。
无非有两种情况（1）D1和D n-1有相同的颜色；（2）D1和D n-1所着颜色不同。
第一种情形，域有k-1种颜色可用，即D1D n-1域所用颜色除外；而且从D1到D n-2的着色方案，和n-2个域的着色方案一一对应。
足球构造中的数学问题足球运动被誉为当今世界第一体育运动，四年一度的世界杯足球赛吸引了数以万计学生的关注。
但调查显示，尽管参加足球运动的学生中有95%知道足球是由黑、白两色皮革私合或缝制而成，但知道黑、白两色皮革的形状、块数的仅有28.2%和 5.6%，至于足球的表面结构与正多面体的关系则很少有人知晓。
为此，以中学学科知识为基础，我们开展了一次富有成效的研究性学习。
一、走访调查通过走访足球生产厂家、体育用品商店、足球教练以及中学体育教师，我们获得了许多与足球有关的知识。
1.球的外形。
足球虽然是球体，但实际上是由黑、白两色皮革勃合或缝制成的多面体加工而成的。
足球不得使用可能伤害运动员的材料，通常用皮革或其他适当材料制作。
其中黑色皮为正五边形，白色皮为正六边形，表面之间具有下列特征:①黑色皮周围都是白色皮;②每两个相邻的多边形恰好有一条公共边;③每个顶点都是三块皮的公共点，且为一黑二白。
(图l).2.相关数据。
正式比赛用球，其大圆的圆周长在68cm至7Icm之间，球的质量应在396 g至453 g之间，充气后其压力应在600g/cm2至1100g/cm2之间。
3.充气时的力学原理。
当空气不断地充人球体内时，球内的空气质量不断增多，此时，球体内压强逐渐变大，可将球皮撑起(球体内部气体压力将平衡大气压力及球皮张力)。
二、研究内容1.黑、白两色皮块数的计算。
依中学数学教材，简单多面体的顶点数V、棱数E及面数F有关系V+F-E=2(欧拉定理)。
假设黑、白两色皮各有x，y块，则面数F=x+y；由于每条棱均为两个面的交线，以棱数E=(5x+6y)/2;每个顶点均为三个面的公共点，所以顶点数v=(5x+6y)/3。
由欧拉定理，有(5x+6y)/3+( x+y)- (5x+6y)/2 =2。
①又因为每块白色皮对应的六边形中有三条边与其他白色皮相连，剩余三条边与黑色皮相接，故6y/2=5x。
②解①②可得x=12，y=20，皮有20块。
专题多面体与球的组合体问题综述11.球与柱体的组合体21.1 球与正方体21.2球与长方体21.3球与正棱柱22球与锥体的组合体32.1 球与正四面体32.2 球与三条侧棱互相垂直的三棱锥32.4 球与其他棱锥43三视图相结合的组合体问题44.球的截面问题5专项训练题球与几何体的组合体问题5综述在各类考试中，与球有关的问题往往是：（1）外接球一个几何体的所有顶点在球上，此球即为外接球，确定其半径的方法主要是：A．将几何体补为长方体或正方体，化为这两种特殊几何体的外接球问题；B．利用外接球的球心的特点〔到几何体所有顶点的距离相等，先确定球心的轨迹，再列等式，解得半径〕解此类题的关键是：球心到多面体的顶点的距离都相等，都等于球的半径，这是确定球心位置的根本依据要知道以下知识：〔1〕正方体，长方体的外接球的球心在体对角线的中点处；〔2〕直棱柱的外接球的球心在高的中点；〔3〕对于底面是三角形的棱锥，需要知道：在空间，到三角形三个顶点距离相等的点，在经过该三角形外心且与该三角形平面垂直的直线上；〔4〕对某些特殊的三棱锥，可以将其补成为正〔长〕方体，三棱锥的外接球就是正〔长〕方体的外接球（2）切球也即球在几何体部，与其所有侧面均相切，这种球的半径往往用体积公式来确定，类似于求三角形接圆的半径问题。
1.球与柱体的组合体1.1 球与正方体如图1所示，正方体1111ABCD A B C D -，设正方体的棱长为a ，,,,E F H G 为棱的中点，O 为球的球心.常见组合方式有三类：一是球为正方体的切球，截面图为正方形EFGH 和其切圆，那么2a OJ r ==； 二是与正方体各棱相切的球，截面图为正方形EFGH 和其外接圆，那么22GO R ==； 三是球为正方体的外接球，截面图为长方形11ACAC 和其外接圆，那么13AO R '==. 例将棱长为2的正方体木块削成一个体积最大的球，那么这个球的外表积为〔〕 A ．2πB ．4πC ．8πD ．16π1.2球与长方体长方体必有外接球，不一定存在切球〔只有为正方体时才有〕. 设长方体的棱长为,,,a b c 其体对角线为l ，那么22222(2)l R a b c ==++，外接球的半径2222l a b c R ++==1.3球与正棱柱下面以正三棱柱为例。
数学必修二多面体知识点
数学必修二中关于多面体的知识点包括：
1. 多面体的定义：多面体是由平面多边形围成的立体图形，其中每个多边形都与它相
邻的多边形共有一条边，并且任意两个平面多边形都可以通过共有的边连接起来。
2. 多面体的分类：根据面的形状和特点，多面体可以分为正多面体和非正多面体。
3. 正多面体：所有面都是相等的正多边形，并且每个顶点都是以同样长度的棱相交的。
常见的正多面体有四面体、六面体和八面体。
4. 非正多面体：其中至少有一个面不是正多边形。
例如，五边形棱锥和五边形棱台就
是非正多面体。
5. 多面体的性质：
- 多面体的面数、顶点数和边数满足欧拉公式：面数 + 顶点数 - 边数 = 2。
- 正多面体的晶体系统有限个，非正多面体的晶体系统无穷个。
- 正多面体的所有内角相等，非正多面体的内角不等。
- 定理：正多面体的面数、顶点数和边数都是可以正整数的。
6. 多面体的展开图：将多面体的各个面展开到一个平面上，连接相邻的面的边，形成
的图形称为多面体的展开图。
展开图可以帮助我们计算多面体的表面积和体积。
7. 多面体的表面积和体积计算：
- 表面积：正多面体的表面积等于每个面积乘以面的个数，非正多面体的表面积等于每个面积乘以面的个数再除以2。
- 体积：对于正多面体，可以使用公式V = (1/3) * S * H来计算体积，其中S为底
面积，H为高。
对于非正多面体，需要将其分解为等腰三角形棱锥或棱台来计算体积。
以上是数学必修二中关于多面体的一些主要知识点，希望能对你有所帮助。
正多面体及足球的转动群
一、正四面体（顶点数：4 棱数：6）转动群：12
1、以顶点为目标的转动群：
1）以顶点—面心为轴（1）1（3）1 8个
2）以棱中—棱中为轴（2）2： 3个
3）不动（1）4： 1个
2、以棱为目标的转动群：
1）以顶点—面心为轴（3）2： 8个
2）以棱中—棱中为轴（1）2（2）2：3个
3）不动（1）6： 1个
3、以面为目标的转动群：
1）以顶点—面心为轴（1）1（3）1： 8个
2）以棱中—棱中为轴（2）2： 3个
3）不动（1）4： 1个
二、正六面体正方体（顶点数：8棱数：12）转动群：24
1、以顶点为目标的转动群：
1）以顶点—顶点为轴（1）2（3）2：8个
2）以棱中—棱中为轴（2）4： 6个
3）以面心—面心为轴（4）2： 6个 90
（2）4： 3个 180
4）不动（1）8： 1个
2、以棱为目标的转动群：
1）以顶点—顶点为轴（3）4： 8个
2）以棱中—棱中为轴（1）2（2）5：6个
3）以面心—面心为轴（4）3： 6个
（2）6： 3个
4）不动（1）12： 1个
3、以面为目标的转动群：
1）以顶点—顶点为轴（3）2： 8个
2）以棱中—棱中为轴（2）3： 6个
3）以面心—面心为轴（1）2（4）1：6个 90度
（1）2（2）2：3个 180度4）不动（1）6： 1个
三、正八面体（顶点数：6 棱数：12）转动群：24
1、以顶点为目标的转动群：
1）以顶点—顶点为轴（1）2（4）1：6个
（1）2（2）2：3个
2）以棱中—棱中为轴（2）3： 6个
3）以面心—面心为轴（3）2： 8个
4）不动（1）6： 1个
2、以棱为目标的转动群：
1）以顶点—顶点为轴（4）3：6个
（2）6：3个
2）以棱中—棱中为轴（1）2（2）5： 6个
3）以面心—面心为轴（3）4： 8个
4）不动（1）12： 1个
3、以面为目标的转动群：
1）以顶点—顶点为轴（4）2：6个 +-90
（2）4：3个 180 2）以棱中—棱中为轴（2）4：6个
3）以面心—面心为轴（1）2（3）2： 8个
4）不动（1）8： 1个
四、正十二面体（顶点数：20 棱数：30）转动群：60
1、以顶点为目标的转动群：
1）以顶点—顶点为轴（1）2（3）6：20个
2）以棱中—棱中为轴（2）10： 15个
3）以面心—面心为轴（5）4： 24个
4）不动（1）20： 1个
2、以棱为目标的转动群：
1）以顶点—顶点为轴（3）10：20个
2）以棱中—棱中为轴（1）2（2）14： 15个
3）以面心—面心为轴（5）6： 24个
4）不动（1）30： 1个
3、以面为目标的转动群：
1）以顶点—顶点为轴（3）4：20个
2）以棱中—棱中为轴（2）6： 15个
3）以面心—面心为轴（1）2（5）2： 24个
4）不动（1）12： 1个
五、正二十面体（顶点数：12 棱数：30）
1、以顶点为目标的转动群：
1）以顶点—顶点为轴（1）2（5）2：24个
2）以棱中—棱中为轴（2）6： 15个
3）以面心—面心为轴（3）4： 20个
4）不动（1）12： 1个
2、以棱为目标的转动群：
1）以顶点—顶点为轴（5）6： 24个
2）以棱中—棱中为轴（1）2（2）14：15个
3）以面心—面心为轴（3）10： 20个
4）不动（1）30： 1个
3、以面为目标的转动群：
1）以顶点—顶点为轴（5）4：24个
2）以棱中—棱中为轴（2）10： 15个
3）以面心—面心为轴（1）2（3）6： 20个
4）不动（1）20： 1个
六、足球（顶点数：60棱数：90五边形：12 六边形：20）
1、以顶点为目标的转动群：
1）以五边行面心—五边行面心为轴（5）12： 24个
2）以棱中—棱中为轴（2）30： 15个
3）以六边行面心—六边行面心为轴（3）20： 20个
4）不动（1）60： 1个
2、以棱为目标的转动群：
1）以五边行面心—五边行面心为轴（5）18： 24个
2）以棱中—棱中为轴（1）2（2）44： 15个
3）以六边行面心—六边行面心为轴（3）30： 20个
4）不动（1）90： 1个
3、以面为目标的转动群：
1）以五边行面心—五边行面心为轴（1）2 （5）6： 24个
2）以棱中—棱中为轴（2）6（2）10： 15个
3）以六边行面心—六边行面心为轴（1）2（3）10： 20个
4）不动（1）12（1）20： 1个。
