杨辉三角 小学数学 精品
- 格式：doc
- 大小：40.51 KB
- 文档页数：4
文档推荐
-
高二数学杨辉三角综合测试题页数:8
-
1.3.2杨辉三角与二项式的性质页数:25
-
高二数学《二项式定理-杨辉三角》详说课件页数:17
-
高中选修杨辉三角页数:14
-
高二数学杨辉三角页数:17
-
高中数学-杨辉三角(2)页数:28
下载文档原格式
合集下载
最新杨辉三角课件精品课件
A
B
由此看来，杨辉三角与纵横(zònghéng)路线图问题有天然的联系
第十六页，共24页。
五、小结 (xiǎojié)
1、杨辉三角蕴含(yùn hán)的基 本性质
2、杨辉三角蕴含的数字(shùzì)排 列规律
第十七页，共24页。
杨辉三角的其它(qítā) 规律
第十八页，共24页。
杨辉三角中若第P行除去(chúqù)1外，P整
C C r1
r
n1
n1
第n行1 Cn1 Cn2
…
Cnr
…
…… … … 第十九页，共24页。
C n2
n1 1
C n1 n
1
练习 （(l0i4à.n上x海í)春1季: 高考）如图，在由二项式系数
(xìshù)所构成的杨辉三角形中，第3_4____行中从
左至右第14与第15个数的比为 2 :.3
第二十一页，共24页。
C a b r kr r k
C
k k
bk
则当n=k+1时，(a b)k1 (a b)k (a b)
(Ck0ak Ck1ak1b1 Ckrakrbr Ckk ak )(a b)
Ck0a k1
C k1a k b
C
r k
1a
k
r
bb1
C
k k
ab
k
C k0a k b
C
r k
a
k
r
b
r
1
C kk 1ab k
研究性课题(kètí)：
杨辉三角
第一页，共24页。
杨辉三角
第0行
1
第1行
11
第2行
第3行 第4行
B
由此看来，杨辉三角与纵横(zònghéng)路线图问题有天然的联系
第十六页，共24页。
五、小结 (xiǎojié)
1、杨辉三角蕴含(yùn hán)的基 本性质
2、杨辉三角蕴含的数字(shùzì)排 列规律
第十七页，共24页。
杨辉三角的其它(qítā) 规律
第十八页，共24页。
杨辉三角中若第P行除去(chúqù)1外，P整
C C r1
r
n1
n1
第n行1 Cn1 Cn2
…
Cnr
…
…… … … 第十九页，共24页。
C n2
n1 1
C n1 n
1
练习 （(l0i4à.n上x海í)春1季: 高考）如图，在由二项式系数
(xìshù)所构成的杨辉三角形中，第3_4____行中从
左至右第14与第15个数的比为 2 :.3
第二十一页，共24页。
C a b r kr r k
C
k k
bk
则当n=k+1时，(a b)k1 (a b)k (a b)
(Ck0ak Ck1ak1b1 Ckrakrbr Ckk ak )(a b)
Ck0a k1
C k1a k b
C
r k
1a
k
r
bb1
C
k k
ab
k
C k0a k b
C
r k
a
k
r
b
r
1
C kk 1ab k
研究性课题(kètí)：
杨辉三角
第一页，共24页。
杨辉三角
第0行
1
第1行
11
第2行
第3行 第4行
杨辉三角课件
1 33 1
1 4641
第5行--
C
0 5
C
1 5
C
2 5
C
3 5
C
4 5
C
5 5
1 5 10 10 5 1
第6行-
C
0 6
C
1 6
C
2 6
C
3 6
C
4 6
C
5 6
C
6 6
1 6 15 20 15 6 1
知识探究3:
(a+b)1
(a+b)2
C10 C11
C
0 2
C12
C
2 2
11 121
(a+b)3
…
)
也就是说, (1+x)n的展开式中的各个
二项式系数的和为2n，且奇数项的二
项式系数和等于偶数的二项式系数和
赋值法
课堂练习:
1、在(a＋b)20展开式中，与第五项二项式系数相同
的项是( C ).
A.第15项 B.第16项 C.第17项 D.第18项
2、在(a＋b)11展开式中，二项式系数最大的项( C ).
C
5 5
C
0 6
C
1 6
C
2 6
C
3 6
C
4 6
C
5 6
C
6 6
总结提炼2:
C = C m
n-m
n
n
与首末两端“等距离”的两个二项式系数相等
第1行———
C
10C
1 1
第2行——
C
0 2
C
1 2
C
2 2
第3行—-
C
数学课件：1.3.2 杨辉三角
间两项,这两项的二项式系数相等并且最大,最大为C������2 = C������2 .
题型一 题型二 题型三 题型四
题型一 杨辉三角的应用
【例1】 在“杨辉三角”中,每行的两端都是1,其余每个数都是它 “肩上”两个数的和,“杨辉三角”开头几行如图所示.
(1)利用“杨辉三角”展开(1-x)6; (2)在“杨辉三角”中哪一行会出现相邻的三个数,它们的比是
12
【做一做2-2】 在(1-x)6的展开式中,含x的奇数次幂的项的系数 和为( )
A.32 B.-32 C.0 D.-64 解析:由 Tr+1=C6������ (-x)r=(-1)rC6������ xr 可知,含 x 的奇数次幂的项的系数 和为-(C61 + C63 + C65)=-32. 答案:B
=
4 5
,
化简得
3 4 4 5
= =
������
������+1-������
������+1 ������-������
,
,
1.理解杨辉三角的意义. 2.掌握二项式系数的性质并会应用.
12
1.杨辉三角 关于(a+b)n展开式的二项式系数,当n取正整数时可以单独列成下 表的形式:
上面的二项式系数表称为“杨辉三角”或“贾宪三角”,在欧洲称为 “帕斯卡三角”.
12
名师点拨 解决与杨辉三角有关的问题的一般方法:观察——分 析——试验——猜想结论——证明.要得出杨辉三角中数的诸多排 列规律,取决于我们的观察能力,观察的方法:横看、竖看、斜看、 连续看、隔行看,从多角度观察.
12
【做一做1】 如图所示,在由二项式系数所构成的杨辉三角中,第
杨辉三角(小学版)
1.两条斜边都是由数字1组成，其余的数则是等于上一行左右两个数字之和. 2.每行数字左右对称，由1开始逐渐变大，然后变小，最后再回到1. 3.第n行的数字个数为n个。 4.n行中第i个数是斜行i-1中前n-1个数之和。
杨辉三角计算演示
杨辉三角的应用 Ⅰ
杨辉三角可以用来帮助解决11的几次方的问题
杨辉三角
Chinese triangle
四年级（4）班
什么是杨辉三角？
杨辉是南宋时期杭州人。在
他1261年所著书中，记录了右边图所 示的三角形数表，这三角形就被称为 杨辉三角。在欧洲直到1623年以后， 法国数学家帕斯卡才发现了同样规律， 因此欧洲人又称这个三角为“帕斯卡三 角”。但是大家从杨辉发现这个规律的 年代与帕斯卡发现这个规律年代相比 就会知道，我国的杨辉发现此规律比 帕斯卡早了300多年。近年来国外也逐 渐承认这项成果属于中国，开始称这 个三角是“中国三角形”。（Chinese triangle）。
大家可以看出11的几次方，也就是n个11连乘答案正好是杨辉三角所 对应的第n行的数字，
很神奇吧！
杨辉三角的应用 Ⅱ
大家请看一下下面的表格能发现什么吗？
对，这就是杨辉三角的又一个应用： 2的n次方也就是第 n行数字之和，很有意思对吧？
概括
杨辉三角除了以上两个应用，我
们还可以在日常生活中来用它来计算最近的 路径问题以及弹子游戏中弹子掉落的概率等 许多问题。 古老的杨辉三角， 即使在我们现代生活中 也能得到充分的利用， 我们中国人的祖先在几 百年前就能最先发现这 个有用的规律，是不是 令我们由衷地为我们中 国灿烂的古代文明心生 自豪之情呢？
杨辉三角上课用PPT课件
(a+b)6…1 6 15 20 15 6 1
观察每一行的第一个和最后一个数有什么特点？
(1)对称性: Cn0 1,Cnn 1
与首末两端“等距离”的两个二项式系数相等．
这就是组合数的性质
1: Cnm
C nm n
第2页/共32页
(a性+b质)1…………… 1 1
(2)递推性:
除(a1+以b)外2…的…每…一个…数…都1等2于它1肩上两个数的和.
第15页/共32页
题型 证明不等式
例20．证明： 当n N*且n 1 2 (1 1)n 3
n
证明 (1
1 )n n
1 Cn1
1 n
Cn2
1 n2
11 Cn2
1 n2
2
通项
Cnk
1 nk
n(n
1)
k
(n !
k
1)
1 nk
nk k!
1 nk
1 k!
(1
1)n n
1
C
1 n
1 n
Cn2
1，1，2，3，5，8，13，21，34，．．．
第21页/共32页
探究：横行规律
第0行
1 2 3
4 5 6 7
8 9 10 11 12 13 14
15
1）杨辉三角中的第1，3，7，15，…行，即第 2n-1行的 各个数字为奇数？
则第2n行的数字有什么特点？除两端的1之外都是偶数.
第22页/共32页
解:?1二项式系数之和为C90 C91 C92 C99 29 512.
解 : 设2x 3y9 a0x9 a1x8y a2x7y2 a9y9. 2令x y 1得各项系数之和为a0 a1 a2 a9 21 319 1.
课件6：1.3.2 杨辉三角
考点二 二项展开式中各项的系数和
例 2 设(1－2x)2 014＝a0＋a1x＋a2x2＋…＋a2 014·x2 014(x∈R)． (1)求 a0＋a1＋a2＋…＋a2 014 的值． (2)求 a1＋a3＋a5＋…＋a2 013 的值． (3)求|a0|＋|a1|＋|a2|＋…＋|a2 014|的值．
和为( )
A．2n＋1
B．2n－1
C．2n＋1－1
D．2n＋1－2
【解析】令 x＝1，则 2＋22＋…＋2n＝2n＋1Байду номын сангаас2. 【答案】D
4．已知(1＋2x－x2)7＝a0＋a1x＋a2x2＋…＋a13x13＋a14x14. (1)求 a0＋a1＋a2＋…＋a14； (2)求 a1＋a3＋a5＋…＋a13.
x
2
n
的展开式中，各项系数和与它的
二项式系数和的比为 32.
(1)求展开式中二项式系数最大的项；
(2)求展开式中系数最大的项．
解：令 x＝1，
则展开式中各项系数和为(1＋3)n＝22n.
又展开式中二项式系数和为 2n，
∴222nn＝2n＝32，n＝5.
(1)∵n＝5，展开式共 6 项，
∴二项式系数最大的项为第三、四两项，
方法小结
二项式系数的有关性质的形成过程体现了观察—— 归纳——猜想——证明的数学方法，并且在归纳证明的过 程中应用了函数、方程等数学思想．大致对应如下：
一点通 解决与杨辉三角有关的问题的一般思路： (1)观察：对题目要横看、竖看、隔行看、连续看，多角 度观察； (2)找规律：通过观察，找出每一行的数之间、行与行之 间的数据的规律．
题组集训
1．如图是一个类似杨辉三角的图形， 则第 n 行的首尾两个数均为________．
杨辉三角优质课件
n 1
n 1 n
C
n n
倒序相加法
思考3.在(3x -2y)20的展开式中，求：(1)二项 式系数最大的项;(2)系数绝对值最大的项;(3) 系数最大的项; 解:(2)设系数绝对值最大的项是第r+1项. 则 r 20 r r r 1 19 r r 1
C 20 3 C 3
r 20
2 C 20 3 2 C
r r 1 20
2
20 r
3
21 r
2
r 1
即
3(r+1)>2(207 r8 5 5
8
所以当r=8时，系数绝对值最大的项为 8 12 8 12 9 20
T C 3 2 x y
即
3(r+1)>2(20-r)
令a=1，b=－1得
C C C C
0 n 2 n 1 n 3 n
1答案 2答案
2 n
启示：在二项式定理中，对a,b赋予一些特定的值， 是解决二项式有关问题的一种重要方法——赋值法。
0 2 1 2 2 2 n 2 n ) (C n ) (C n ) (C n ) C2 思考2求证: (Cn n. 略证：由(1+x)n(1+x)n=(1+x)2n，两边展开 后比较xn的系数得：
m m m 1 C C 这就是组合数的性质 2: C n 1 n n
可运用函数的观点，结合“杨辉三角”和函数图象， 研究二项式系数的性质． f( r ) 20 n (a+b) 展开式的二项式系数是
C , C , C , , C ， , C .
0 n
1 n
n 1 n
C
n n
倒序相加法
思考3.在(3x -2y)20的展开式中，求：(1)二项 式系数最大的项;(2)系数绝对值最大的项;(3) 系数最大的项; 解:(2)设系数绝对值最大的项是第r+1项. 则 r 20 r r r 1 19 r r 1
C 20 3 C 3
r 20
2 C 20 3 2 C
r r 1 20
2
20 r
3
21 r
2
r 1
即
3(r+1)>2(207 r8 5 5
8
所以当r=8时，系数绝对值最大的项为 8 12 8 12 9 20
T C 3 2 x y
即
3(r+1)>2(20-r)
令a=1，b=－1得
C C C C
0 n 2 n 1 n 3 n
1答案 2答案
2 n
启示：在二项式定理中，对a,b赋予一些特定的值， 是解决二项式有关问题的一种重要方法——赋值法。
0 2 1 2 2 2 n 2 n ) (C n ) (C n ) (C n ) C2 思考2求证: (Cn n. 略证：由(1+x)n(1+x)n=(1+x)2n，两边展开 后比较xn的系数得：
m m m 1 C C 这就是组合数的性质 2: C n 1 n n
可运用函数的观点，结合“杨辉三角”和函数图象， 研究二项式系数的性质． f( r ) 20 n (a+b) 展开式的二项式系数是
C , C , C , , C ， , C .
0 n
1 n
杨辉三角PPT优秀课件
B 1
1 1 4
A
1 1 3
1
3
2
1
1
A
6 4 1 5 10 5 10 15 20 15 35 35 B70
2、杨辉三角的对称性：
C C .
r n
nr n
3、杨辉三角的第 n行就是二项式 (a b) 的展开式的系数，即：
n
(a b) C a C a b
n r 0 n n 1 n
2.1杨辉三角(1)
杨辉最重要的著作是《详解九章算法》． 为了使《九章算术》便于自学，杨辉对 该书的246个问题中较难的80题作了详解， 并增添了“图解、乘除算法和纂类”三卷． “详解”包括三个方面：一是“解题”，即解 释题意、名词术语，校勘文字，并对题目 作出评注；二是“细草”，即详细的解题过 程及必要的图示；三是“比类”，即增选与 原题算法相同或类似的例题进行对照分析． “纂类”是把《九章算术》中的全部问题按 解题方法由浅入深的顺序重新整理分类．
杨辉三角与“纵横路线图” “纵横路线图”是数学中的一类有趣 的问题．图 1 是某城市的部分街道 图，纵横各有五条路，如果从 A 处 走到 B 处 ( 只能由北到南，由西向 东 ) ，那么有多少种不同的走法？
我们把图顺时针转 45 度，使 A 在 正上方， B 在正下方，然后在交叉 点标上相应的杨辉三角数．有趣的 4 是， B 处所对应的数 C 8 =70 ， 正好是答案 ( 70) ． 一般地 , 每个交点上的杨辉三角数， 就是从 A 到达该点的方法数．由此 看来，杨辉三角与纵横路线图问题 有天然的联系．
n1
Ca
r n
n r
b C b
n n n
请用数学归纳法证明这一性质 。
《杨辉三角》_精品教学PPT人教版1
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
解析：
由图1我们能发现，第1行中的数是 C10，C11 第2行中的数是 C02，C12，C22 第3行中的数是 C03，C13，C32，C33 则第n行中的数是 Cn0，C1n，Cn2， ，Cnn 设第n行中从左到右第14与第15个数的比为2 : 3
则 C1n3·C1n4 = 2 : 3 ，解得 n = 34
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
2.(1-x3)•(1+x)10的展开式中含x4的项的系数 2为00_____(用数字作答).
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
针对性练习
1. 如图１，在由二项式系数所构成的杨辉三 角中，第___3_4__行中从左到右第14与第15个数的 比为2:3 .
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版) 《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
课堂小结
1.二项式系数的三条性质
（1）对称性; （2）增减性与最大值; （3）各二项式系数的和; （4）递推性（杨辉三角中）.
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
解析：
由图1我们能发现，第1行中的数是 C10，C11 第2行中的数是 C02，C12，C22 第3行中的数是 C03，C13，C32，C33 则第n行中的数是 Cn0，C1n，Cn2， ，Cnn 设第n行中从左到右第14与第15个数的比为2 : 3
则 C1n3·C1n4 = 2 : 3 ，解得 n = 34
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
2.(1-x3)•(1+x)10的展开式中含x4的项的系数 2为00_____(用数字作答).
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
针对性练习
1. 如图１，在由二项式系数所构成的杨辉三 角中，第___3_4__行中从左到右第14与第15个数的 比为2:3 .
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版) 《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
课堂小结
1.二项式系数的三条性质
（1）对称性; （2）增减性与最大值; （3）各二项式系数的和; （4）递推性（杨辉三角中）.
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
杨辉三角 课件
二项式系数表
“杨辉三角”
杨辉三角
《
九
章
杨
算
辉
术
》
本积
商实
《 九
平方
章
立方
算
术
三乘
》 杨
四乘
辉
五乘
《详解九章算法》中记载的表
(a + b)n Cn0an Cn1an1b Cnranrbr Cnnbn
(a+b)1 (a+b)2 (a+b)3 (a+b)4 (a+b)5 (a+b)6
n
n1 n1
C C 当n是奇数时，中间的两项
2， 2 相等，
n
n
且同时取得最大值。
2 （4）二项式系数之和: n (由赋值法求得 )
2、 数学方法 ： 赋值法 、归纳猜想
ቤተ መጻሕፍቲ ባይዱ
(a+b)1 (a+b)2 (a+b)3 (a+b)4 (a+b)5 (a+b)6
n 1时，C10 C11 2;
归纳猜想：Cn0 Cn1 Cn2 …+Cnn
? n 2时，C20 C21 C22 4;
n n 3时，C30 C31 C32 C33 8;
2 ……
n 6时，C60 C61 C62 C63 C64 C65 C66 64;
课堂练习:
1、在(x y)n展开式中只有第5项的二项式系数最大，
8 则n
2、在(x 1)n 展开式中，第3项的二项式系数与第5项
6 x
的二项式系数相等，则n
1 3、在(2x2 1)6展开式中,二项式系数和为 x
64
各项系数之和为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
杨辉三角
人教版小学数学五年级下期第115页第10题，涉及著名的“杨辉三角”，
对此，教参中已有所介绍。
为了提高学生的学习兴趣，加深对“杨辉三角”的理解，增强学生的民族自豪感和爱国热情，下面推荐一个有趣的数学游戏。
老师出示一张图(有条件的可以使用多媒体)：
宣布：“现在和同学们玩一个有趣的数学游戏。
请一位同学在这个图的最下面一行6个圆圈里任意各填一个一位数，我随即在顶端那个圆圈里写一个数。
然后，大家按照图中的连线，算出最下面那行相邻两个圆圈里的数的和，填入上一行的圆圈里。
自下而上照这样进行下去，直到算出顶端那个圆圈里应该填的数，一定跟我已经填好的数一样。
哪位同学愿意试一试？”
等那位同学把最下面一行的6个数填好以后，老师迅速算出左起第三、四两个数的和的10倍，加上第二、五两个数的和的5倍，再加上第一、六两个数，得数就是顶端那个圆圈里应该填的数。
比如，从左到右，学生所填的数是4、1、8、6、2、3，老师就应该填10
×(8＋6)＋5×(1＋2)＋(4＋3)＝140＋15＋7＝162。
这是为什么呢？原来，“杨辉三角”中的数是有规律的。
规律是：自上而下，每个圆圈里的数等于与它相连的，上一行圆圈里的数的和。
比如，第三行中间圆圈里的数之所以是2，就因为与它相连的第二行两个圆圈里的数都是1，1＋1＝2。
依此类推。
游戏相当于把上面的过程倒回去，所以要把圆圈里的数分别乘上1、5、10、10、5、1。
等玩过两三次以后，学生一定会急于知道老师是怎样做到未卜先知的，甚至有些爱动脑筋的学生，已经在开始探求其中的奥秘了。
这时，可以启发学生用学过的“用字母表示数”的方法，看看最下面那行所填的6个数，在整个计算过程中究竟各用了几次。
设：第六行所填的6个数依次为A、B、C、D、E、F。
第五行就是A＋B、B ＋C、C＋D、D＋E、E＋F；第四行就是A＋2B＋C、B＋2C＋D、C＋2D＋E、D＋2E＋F；第三行就是A＋3B＋3C＋D、B＋3C＋3D＋E、C＋3D＋3E＋F；第二行就是A＋4B＋6C＋4D＋E、B＋4C＋6D＋4E＋F；顶端的数就是A＋5B＋10C＋10D ＋5E＋F，即10(C＋D)＋5(B＋E)＋(A＋F)。
从而得出前面所总结出的方法。
“杨辉三角”在数学中有着重要作用，同时又具有直观形象的特点，对于培养学生的思维能力很有好处，值得给学生提供一个加深印象的机会。
杨辉三角
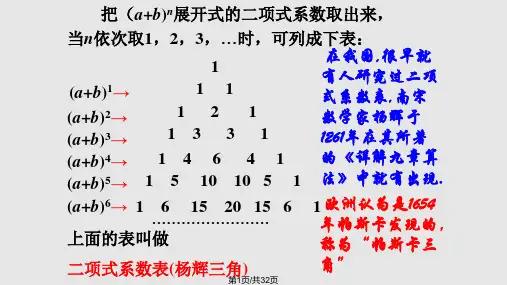
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
……
中还隐藏着许多奥秘：
请看这些斜线上的数：
自然数 1
三角形数 1 1
四面体数 1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
……
一、自然数：1，2，3，4，…
求前n个自然数的和，无需使用公式，答案就在第n个自然数的左下方。
比如，前4个自然数的和，就在第4个自然数4的左下方，是10。
前5个自
然数的和，就在第5个自然数5的左下方，是15。
依此类推。
二、三角形数：1，3，6，10，…
三角形数就是可以用点“排”成三角形的数。
最顶端1个点，下一排2个点，再下一排3个点，再下一排4个点，5个点，6个点……所以，三角形数依次是1，1＋2＝3，1＋2＋3＝6，1＋2＋3＋4＝10，……即1，3，6，10，…
求前n个三角形数的和，无需使用公式，答案就在第n个三角形数的左下方。
比如，前4个三角形数的和，就在第4个三角形数10的左下方，是20。
前5个三角形数的和，就在第5个三角形数15的左下方，是35。
依此类推。
三、四面体数：1，4，10，20，…
四面体数就是可以用三角形数“垒”成四面体的数。
最顶端1个点，下一层3个点，再下一层6个点，再下一层10个点，15个点，21个点……所以，四面体数依次是1，1＋3＝4，1＋3＋6＝10，1＋3＋6＋10＝20，……即1，4，10，20，…
求前n个四面体数的和，无需使用公式，答案就在第n个四面体数的左下方。
比如，前3个四面体数的和，就在第3个四面体数10的左下方，是15。
前4个四面体数的和，就在第4个四面体数20的左下方，是35。
依此类推。
最让人感到意外的是，“杨辉三角”竟然还与“菲波那契数列”有着密切的关系。
请看下图：（图中的斜线可以一直画下去）
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
……
斜线上数的和，依次是1，1，1＋1＝2，1＋2＝3，1＋3＋1＝5，1＋4＋3＝8，1＋5＋6＋1＝13，1＋6＋10＋4＝21，1＋7＋15＋10＋1＝34，……
1，1，2，3，5，8，13，21，34，……不正是菲波那契数列吗？
“杨辉三角”真称得上是一个数学宝藏，它的这些奇妙之处都是后来陆续被发现的，究竟其中还隐藏着那些奥秘，仍然是一个未知数。
发掘宝藏，需要
兴趣和毅力，也许新的发现正在向你招手呢！。