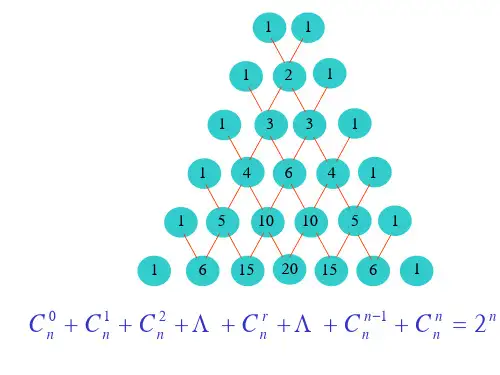
高中数学-杨辉三角(2)

2018学年第⼆学期⾼⼆数学《杨辉三⾓与⼆项式系数的性质》学案含答案1.3.2“杨辉三⾓”与⼆项式系数的性质学习⽬标 1.了解杨辉三⾓，会⽤杨辉三⾓求⼆项式乘⽅次数不⼤时的各项的⼆项式系数.2.理解⼆项式系数的性质并灵活运⽤(重、难点).知识点1杨辉三⾓的特点(1)在同⼀⾏中每⾏两端都是1，与这两个1等距离的项的系数相等；(2)在相邻的两⾏中，除1外的每⼀个数都等于它“肩上”两个数的和，即C r n＋1＋C r n.＝C r－1n【预习评价】(1)杨辉三⾓的第n⾏数字规律与⼆项展开式有何联系？提⽰杨辉三⾓的第n⾏数字规律是⼆项式(a＋b)n展开式的⼆项式系数，即(a ＋b)n＝C0n a n＋C1n a n－1b1＋…＋C r n a n－r b r＋…＋C n n b n.(2)C03＋C14＋C25＋…＋C1821＝________.解析原式＝C04＋C14＋C25＋…＋C1821＝C15＋C25＋…＋C1821＝…＝C1721＋C1821＝C1822＝C422＝7 315.答案7 315知识点2⼆项式系数的性质相等，且同时取得最⼤值【预习评价】(1)⼆项展开式中系数最⼤项是中间⼀项(共奇数项)或中间两项(共偶数项)，这种说法对吗？提⽰错误.⼆项展开式中项的系数与⼆项式系数是不同的，⼆项式系数最⼤项是中间⼀项(共奇数项)或中间两项(共偶数项)，但是项的系数的最⼤值与项其他数字因数的⼤⼩有关.(2)在(x ＋y )n 的展开式中，第4项与第8项的系数相等，则展开式中系数最⼤的项是( ) A.第6项B.第5项C.第5，6项D.第6，7项解析由题意，得第4项与第8项的系数相等，则其⼆项式系数也相等，∴C 3n ＝C 7n ，由组合数的性质，得n ＝10.∴展开式中⼆项式系数最⼤的项为第6项，它也是系数最⼤的项. 答案 A题型⼀与杨辉三⾓有关的问题【例1】如图在“杨辉三⾓”中，斜线AB 的上⽅，从1开始箭头所⽰的数组成⼀个锯齿形数列：1，2，3，3，6，4，10，5，…，记其前n 项和为S n ，求S 19的值.解由题图知，数列中的⾸项是C22，第2项是C12，第3项是C23，第4项是C13，…，第17项是C210，第18项是C110，第19项是C211.∴S19＝(C12＋C22)＋(C13＋C23)＋(C14＋C24)＋…＋(C110＋C210)＋C211＝C23＋C24＋C25＋…＋C211＋C211＝C33＋C23＋C24＋C25＋…＋C211－1＋C211＝C312－1＋C211＝274.规律⽅法解决与杨辉三⾓有关问题的⼀般思路(1)观察找出每⼀⾏数据间的相互联系以及⾏与⾏间数据的相互联系.(2)将数据间的这种联系⽤数学式表达出来，使问题得解.(3)注意观察⽅向：横看、竖看、斜看、连续看、隔⾏看，从多⾓度观察.【训练1】如图，在由⼆项式系数所构成的杨辉三⾓中，第________⾏中从左到右第14与第15个数的⽐为2∶3.第0⾏1第1⾏1 1第2⾏12 1第3⾏133 1第4⾏1464 1第5⾏1510105 1………解析设第n⾏从左⾄右第14与第15个数之⽐为2∶3，则C13n∶C14n＝2∶3.∴3C13n＝2C14n，即3·n！13！·（n－13）！＝2·n！14！·（n－14）！，得：3n－13＝214，∴n＝34.答案34【例2】已知(2x －1)5＝a 0x 5＋a 1x 4＋a 2x 3＋a 3x 2＋a 4x ＋a 5，求a 0＋a 1＋a 2＋a 3＋a 4＋a 5.解令x ＝1，得：(2×1－1)5＝a 0＋a 1＋a 2＋a 3＋a 4＋a 5，∴a 0＋a 1＋a 2＋a 3＋a 4＋a 5＝1.【迁移1】 (变换所求)例2条件不变，求|a 0|＋|a 1|＋|a 2|＋|a 3|＋|a 4|＋|a 5|. 解∵(2x －1)5的展开式中偶数项的系数为负值，∴|a 0|＋|a 1|＋|a 2|＋|a 3|＋|a 4|＋|a 5|＝a 0－a 1＋a 2－a 3＋a 4－a 5. 令x ＝－1，得：[2×(－1)－1]5＝－a 0＋a 1－a 2＋a 3－a 4＋a 5，即a 0－a 1＋a 2－a 3＋a 4－a 5＝－(－3)5＝35，∴|a 0|＋|a 1|＋|a 2|＋|a 3|＋|a 4|＋|a 5|＝35＝243.【迁移2】 (变换所求)例2条件不变，求a 1＋a 3＋a 5. 解由上题得a 0＋a 1＋a 2＋a 3＋a 4＋a 5＝1，a 0－a 1＋a 2－a 3＋a 4－a 5＝243，两式相减得a 1＋a 3＋a 5＝12×(1－243)＝－121.规律⽅法 (1)赋值法是求⼆项展开式系数及有关问题的常⽤⽅法，注意取值要有利于问题的解决，可以取⼀个值或⼏个值，也可以取⼏组值，解决问题时要避免漏项.(2)⼀般地，对于多项式f (x )＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，各项系数和为f (1)，奇次项系数和为12[f (1)－f (－1)]，偶次项系数和为12[f (1)＋f (－1)]，a 0＝f (0). 【训练2】已知(1－3x )8＝a 0＋a 1x ＋…＋a 7x 7＋a 8x 8.求： (1)a 0＋a 1＋…＋a 8； (2)a 0＋a 2＋a 4＋a 6＋a 8；(3)|a 0|＋|a 1|＋|a 2|＋…＋|a 8|.解 (1)令x ＝1，得a 0＋a 1＋…＋a 8＝(－2)8＝256.① (2)令x ＝－1，得a 0－a 1＋a 2－a 3＋a 4－a 5＋a 6－a 7＋a 8＝48.②①＋②，得2(a 0＋a 2＋a 4＋a 6＋a 8)＝28＋48，∴a 0＋a 2＋a 4＋a 6＋a 8＝12×(28＋48)＝32 896.(3)由于(1－3x )8＝C 08＋C 18×(－3x )＋C 28×(－3x )2＋…＋C 88×(－3x )8＝a 0＋a 1x ＋a 2x 2＋…＋a 8x 8，故a 0，a 2，a 4，a 6，a 8＞0，a 1，a 3，a 5，a 7＜0，∴|a 0|＋|a 1|＋|a 2|＋…＋|a 8|＝a 0－a 1＋a 2－a 3＋…＋a 8＝48＝65 536. 题型三⼆项式系数性质的应⽤【例3】已知f (x )＝(3x 2＋3x 2)n 展开式中各项的系数和⽐各项的⼆项式系数和⼤992.(1)求展开式中⼆项式系数最⼤的项； (2)求展开式中系数最⼤的项.解 (1)令x ＝1，则⼆项式各项系数的和为f (1)＝(1＋3)n ＝4n ，⼜展开式中各项的⼆项式系数之和为2n .由题意知，4n －2n ＝992. ∴(2n )2－2n －992＝0，∴(2n ＋31)(2n －32)＝0，∴2n ＝－31(舍)或2n ＝32，∴n ＝5.由于n ＝5为奇数，所以展开式中⼆项式系数最⼤的项为中间两项，它们分别是 T 3＝C 25(x 23)3(3x 2)2＝90x 6， T 4＝C 35(x 23)2(3x 2)3＝270x 223.(2)展开式的通项公式为T r ＋1＝C r 53r·x 23(5＋2r ).假设T r ＋1项系数最⼤，则有C r 5·3r ≥C r －15·3r －1，C r 5·3r ≥C r ＋15·3r ＋1，∴5！（5－r ）！r ！×3≥5！（6－r ）！（r －1）！，5！（5－r ）！r ！≥5！（4－r ）！（r ＋1）！×3.∴3r ≥16－r ，15－r ≥3r ＋1.∴72≤r ≤92，∵r ∈N ，∴r ＝4.∴展开式中系数最⼤的项为T 5＝C 45·34x 263＝405x 263. 规律⽅法 (1)求⼆项式系数最⼤的项，要依据⼆项式系数的性质对(a ＋b )n 中的n 进⾏讨论，n 为奇数时中间两项的⼆项式系数最⼤；n 为偶数时，中间⼀项的⼆项式系数最⼤.(2)求展开式中系数最⼤项与求⼆项式系数最⼤项是不同的.求展开式系数最⼤的项，如求(a ＋bx )n (a 、b ∈R 展开式中系数最⼤的项，⼀般是采⽤待定系数法.设展开式各项系数分别为A 1，A 2，…，A n ＋1，且第r ＋1项系数最⼤，应⽤A r ≥A r －1， A r ≥A r ＋1解出r 来，即得系数最⼤的项. 【训练3】已知? ????x －2x 2n(n ∈N *)的展开式中第5项的系数与第3项的系数的⽐是10∶1.(1)求展开式中各项系数的和； (2)求展开式中含x 32的项；(3)求展开式中系数的绝对值最⼤的项.解∵? ????x －2x 2n 的展开式的通项是T r ＋1＝C r n (x )n －r ·－2x 2r＝(－2)r C rn x n －5r 2(0≤r ≤n ，r ∈N )，∴T 5＝T 4＋1＝24C 4n x n 2－10，T 3＝T 2＋1＝22C 2n x n2－5.∵24C 4n 22C 2n＝101，∴n 2－5n －24＝0，解得n ＝8或n ＝－3(舍去).(1)令x ＝1，则? ????x －2x 28＝(1－2)8＝1，即所求各项系数的和为1. (2)展开式的通项为T r ＋1＝(－2)r C r8x 8－5r 2(0≤r ≤8，r ∈N ).令8－5r 2＝32，得r ＝1，∴展开式中含x 32的项为T 2＝T 1＋1＝(－2)1C 18x 32＝－16x 32.(3)展开式的第r 项、第r ＋1项、第r ＋2项的系数的绝对值分别为C r －182r －1，C r 82r ，C r ＋182r ＋1.若第r ＋1项的系数绝对值最⼤，则有C r －182r －1≤C r 82r ，C r 82r ≥C r ＋182r ＋1，解得5≤r ≤6，故系数的绝对值最⼤的项为第6项和第7项，即 T 6＝－1 792x －172，T 7＝1 7921x 11.课堂达标1.(1＋x )2n ＋1的展开式中，⼆项式系数最⼤的项所在的项数是( ) A.n ，n ＋1B.n －1，nC.n ＋1，n ＋2D.n ＋2，n ＋3解析 2n ＋1为奇数，展开式中中间两项的⼆项式系数最⼤，分别为第? ????2n ＋1－12＋1项，第? ????2n ＋1＋12＋1项，即第(n ＋1)项与第(n ＋2)项.故选C. 答案 C2.设(x 2＋1)(2x ＋1)9＝a 0＋a 1(x ＋2)＋a 2(x ＋2)2＋…＋a 11(x ＋2)11，则a 0＋a 1＋a 2＋…＋a 11的值为( ) A.－2B.－1C.1D.2解析令x ＝－1，则原式化为 [(－1)2＋1][2×(－1)＋1]9＝－2＝a 0＋a 1(2－1)＋a 2(2－1)2＋…＋a 11(2－1)11，∴a 0＋a 1＋a 2＋…＋a 11＝－2. 答案 A3.在(1＋x )＋(1＋x )2＋…＋(1＋x )6的展开式中，x 2的系数为________.解析 (1＋x )＋(1＋x )2＋…＋(1＋x )6的展开式中x 2的系数为C 22＋C 23＋C 24＋C 25＋C 26＝35. 答案 354.设(3x －2)6＝a 0＋a 1(2x －1)＋a 2(2x －1)2＋…＋a 6(2x －1)6，则a 1＋a 3＋a 5a 0＋a 2＋a 4＋a 6＝________.解析令x ＝1，得a 0＋a 1＋a 2＋…＋a 6＝1，令x ＝0，得a 0－a 1＋a 2＋…＋a 6＝64，两式相减，得2(a 1＋a 3＋a 5)＝－63，两式相加，得2(a 0＋a 2＋a 4＋a 6)＝65，故a 1＋a 3＋a 5a 0＋a 2＋a 4＋a 6＝－6365. 答案－63655.已知(2x －1)n ⼆项展开式中，奇次项系数的和⽐偶次项系数的和⼩38，求C 1n ＋C 2n ＋C 3n ＋…＋C n n 的值.解设(2x －1)n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，且奇次项的系数和为A ，偶次项的系数和为B .则A ＝a 1＋a 3＋a 5＋…，B ＝a 0＋a 2＋a 4＋a 6＋….由已知可知：B－A＝38.令x＝－1，得：a0－a1＋a2－a3＋…＋a n(－1)n＝(－3)n，即：(a0＋a2＋a4＋a6＋…)－(a1＋a3＋a5＋a7＋…)＝(－3)n.即：B－A＝(－3)n.∴(－3)n＝38＝(－3)8，∴n＝8.由⼆项式系数性质可得：C1n＋C2n＋C3n＋…＋C n n＝2n－C0n＝28－1.课堂⼩结1.⼆项式系数的性质可从杨辉三⾓中直观地看出.2.求展开式中的系数或展开式中的系数的和、差的关键是给字母赋值，赋值的选择则需根据所求的展开式系数和特征来确定.⼀般地对字母赋的值为0，1或－1，但在解决具体问题时要灵活掌握.3.注意以下两点：(1)区分开⼆项式系数与项的系数.(2)求解有关系数最⼤时的不等式组时，注意其中r∈{0，1，2，…，n}的范围.基础过关1.已知(a＋b)n的⼆项展开式中只有第5项的⼆项式系数最⼤，则n等于()A.11B.10C.9D.8解析∵(a＋b)n的⼆项展开式中只有第5项的⼆项式系数最⼤，∴⼆项展开式共有9项，即n＋1＝9，∴n＝8.答案 D2.(x－1)11展开式中x的奇次项系数之和是()A.－2 048B.－1 023C.－1 024D.1 024解析(x－1)11＝a0x11＋a1x10＋a2x9＋…＋a11，令x＝－1，则－a0＋a1－a2＋…＋a11＝－211，令x＝1，则a0＋a1＋a2＋…＋a11＝0，∴a 0＋a 2＋a 4＋…＋a 10＝210＝1 024. 答案 D3.(1＋x )＋(1＋x )2＋…＋(1＋x )n 的展开式中各项系数和为( ) A.2n ＋1 B.2n －1 C.2n ＋1－1D.2n ＋1－2解析令x ＝1，则2＋22＋…＋2n ＝2n ＋1－2. 答案 D4.若C 2n ＋620＝C n ＋220(n ∈N *)，且(2－x )n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n，则a 0－a 1＋a 2－…＋(－1)n a n ＝________.解析由C 2n ＋620＝C n ＋220可知n ＝4，令x ＝－1，可得a 0－a 1＋a 2－…＋(－1)n a n ＝81. 答案 815.在(a －b )10的⼆项展开式中，系数最⼩的项是________.解析在(a －b )10的⼆项展开式中，奇数项的系数为正，偶数项的系数为负，且偶数项系数的绝对值为对应的⼆项式系数，因为展开式中第6项的⼆项式系数最⼤，所以系数最⼩的项为T 6＝C 510a 5(－b )5＝－252a 5b 5.答案－252a 5b 56.若x 4(x ＋3)8＝a 0＋a 1(x ＋2)＋a 2(x ＋2)2＋…＋a 12(x ＋2)12，求log 2(a 1＋a 3＋…＋a 11)的值.解令x ＝－1，∴28＝a 0＋a 1＋a 2＋…＋a 11＋a 12. 令x ＝－3，∴0＝a 0－a 1＋a 2－…－a 11＋a 12，∴28＝2(a 1＋a 3＋…＋a 11)，∴a 1＋a 3＋…＋a 11＝27，∴log 2(a 1＋a 3＋…＋a 11)＝log 227＝7.7.设a ≠0，n 是⼤于1的⾃然数，? ?1＋x a n 的展开式为a 0＋a 1x ＋a 2x 2＋…＋a n x n .若点A i (i ，a i )，(i ＝0，1，2)的位置如图所⽰，求a 的值.解由题意知，A 0(0，1)，A 1(1，3)，A 2(2，4). 故a 0＝1，a 1＝3，a 2＝4. 由? ?1＋x a n 的展开式的通项知， T r ＋1＝C r n ? ???x a r(r ＝0，1，2，…，n ).故C 1n a ＝3，C 2na 2＝4，解得a ＝3.能⼒提升8.在?1x ＋51x 3n的展开式中，所有奇数项系数之和为1 024，则中间项系数是( ) A.330B.462C.682D.792解析∵⼆项式的展开式中所有项的⼆项式系数和为2n ，⽽所有偶数项的⼆项式系数和与所有奇数项的⼆项式系数和相等，故由题意得2n －1＝1 024，∴n ＝11，∴展开式共12项，中间项为第六项、第七项，其系数为C 511＝C 611＝462.答案 B9.(1＋ax ＋by )n 的展开式中不含x 的项的系数的绝对值的和为243，不含y 的项的系数的绝对值的和为32，则a ，b ，n 的值可能为( ) A.a ＝2，b ＝－1，n ＝5 B.a ＝－2，b ＝－1，n ＝6 C.a ＝－1，b ＝2，n ＝6D.a ＝1，b ＝2，n ＝5解析根据展开式的特点，通过特殊值法找到符合要求的各项系数的绝对值的和，通过⽅程组解决.只要令x＝0，y＝1，即得到(1＋ax＋by)n的展开式中不含x 的项的系数的和为(1＋b)n，令x＝1，y＝0，即得到(1＋ax＋by)n的展开式中不含y的项的系数的和为(1＋a)n.如果a，b是正值，这些系数的和也就是系数绝对值的和，如果a，b中有负值，相应地，分别令y＝－1，x＝0；x＝－1，y＝0.此时的和式分别为(1－b)n，(1－a)n，由此可知符合要求的各项系数的绝对值的和为(1＋|b|)n，(1＋|a|)n.根据题意(1＋|b|)n＝243＝35，(1＋|a|)n＝32＝25，因此n＝5，|a|＝1，|b|＝2.故选D.答案 D10.设m为正整数，(x＋y)2m展开式的⼆项式系数的最⼤值为a，(x＋y)2m＋1展开式的⼆项式系数的最⼤值为b，若13a＝7b，则m＝________.解析由题知a＝C m2m，b＝C m＋12m＋1，∴13C m2m＝7C m＋12m＋1，即13×（2m）！m！m！＝7×（2m＋1）！（m＋1）！m！，解得m＝6.答案 611.(a＋x)(1＋x)4的展开式中x的奇数次幂项的系数之和为32，则a＝________. 解析(1＋x)4展开式的通项为T r＋1＝C r4x r，由题意可知a(C14＋C34)＋C04＋C24＋C44＝32，解得a＝3.答案 312.在(2x－3y)10的展开式中，求：(1)各项的⼆项式系数的和；(2)奇数项的⼆项式系数的和与偶数项的⼆项式系数的和；(3)各项系数之和；(4)奇数项系数的和与偶数项系数的和.解在(2x－3y)10的展开式中：(1)各项的⼆项式系数的和为C 010＋C 110＋…＋C 1010＝210＝1 024. (2)奇数项的⼆项式系数的和为C 010＋C 210＋…＋C 1010＝29＝512. 偶数项的⼆项式系数的和为C 110＋C 310＋…＋C 910＝29＝512.(3)设(2x －3y )10＝a 0x 10＋a 1x 9y ＋a 2x 8y 2＋…＋a 10y 10(*)，各项系数之和即为a 0＋a 1＋a 2＋…＋a 10，由于(*)是恒等式，故可⽤“赋值法”求解.令(*)中x ＝y ＝1，得各项系数之和为(2－3)10＝(－1)10＝1.(4)奇数项系数的和为a 0＋a 2＋a 4＋…＋a 10，偶数项系数的和为a 1＋a 3＋a 5＋…＋a 9.由(3)知a 0＋a 1＋a 2＋…＋a 10＝1. ①令(*)中x ＝1，y ＝－1，得a 0－a 1＋a 2－a 3＋…＋a 10＝510. ②①＋②，得2(a 0＋a 2＋…＋a 10)＝1＋510，故奇数项系数的和为1＋5102；①－②，得2(a 1＋a 3＋…＋a 9)＝1－510，故偶数项系数的和为1－5102.13.(选做题)已知(3x ＋x 2)2n 的展开式的系数和⽐(3x －1)n 的展开式的系数和⼤992，求? ?2x －1x 2n 的展开式中：(1)⼆项式系数最⼤的项； (2)系数的绝对值最⼤的项.解由题意得22n －2n ＝992，解得n ＝5.(1)? ?2x －1x 10的展开式中第6项的⼆项式系数最⼤，即T 6＝C 510·(2x )5·?－1x 5＝－8 064.(2)设第k ＋1项的系数的绝对值最⼤，则T k ＋1＝C k 10·(2x )10－k ·?－1x k＝(－1)k ·C k 10·210－k ·x 10－2k . ∴C k 10·210－k ≥C k －110·210－k ＋1，C k 10·210－k ≥C k ＋110·210－k －1，得C k 10≥2C k －110，2C k 10≥C k ＋110，即11－k ≥2k ，2（k ＋1）≥10－k . ∴83≤k ≤113，∴k ＝3，故系数的绝对值最⼤的是第4项 T 4＝(－1)3C 310·27·x 4＝－15 360x 4.。

《杨辉三角》教学设计一、教材分析《杨辉三角》是高中数学新课标人教B版选修2-3教材第1.3.2节的内容。

本节课是在学生学习了两个计数原理、组合及组合数的性质后，又具体学习了二项式定理、二项式系数等概念的基础上进行的。

“杨辉三角”的内涵实际上就是二项式系数的性质，其内容丰富，值得学生深入探讨。

对于杨辉三角所蕴含的规律，学生不难发现，而难点就在于如何把学生通过观察发现的规律进行归纳，进而推理论证，揭示其数学本质。

本节课利用了转化和化归的数学思想，把对观察得到的规律的证明化归为组合数性质的应用上。

从知识发生发展过程的角度上看，学生可以从直观上很好地观察发现杨辉三角中蕴含的数字规律，但对于高二的学生，他们思考问题的思维已经不仅仅满足于“知其然”，他们更渴望的是“知其所以然”，在老师适当的点拨下，学生能很自然地联系到上位知识，即组合数的性质与二项式系数的联系，通过师生合作完成知识发展过程的探究，这符合学生的认知规律，也体现了互助学习的价值观教育。

二、学情分析对于高二的学生来说，他们已经具备了比较理性的思考，对发现的规律能够尝试证明。

同时学生已掌握了组合及组合数的性质，这是突破本节课难点的基础。

本节课授课班级为普通班，在数学科的学习特点是个体存在较大差距，但学习积极性都很高。

另外，该班设有合作基层小组①，即小组内拥有稳定的成员，他们之间相互支持、鼓励和帮助，小组内部及小组之间有了一定的解决问题的能力，但对于本节课的难点——证明规律，学生还需要在老师的指导下共同完成。

三、教学目标：本节课让学生掌握二项展开式中的二项式系数的基本性质及其推导方法；通过对杨辉三角中蕴含的数字规律的初步探究，培养学生发现问题、提出问题、经过分析——猜想——证明以后解决问题的能力，激励学生自主创新；通过从不同的角度观察杨辉三角，培养学生要从多角度看问题的意识，提高学生解决实际问题的能力，在学习中鼓励学生在学习中学会交流、合作，培养学生团结协作的精神，同时，通过杨辉三角，了解中华优秀传统文化中的数学成就，体会其中的数学文化，培养学生的爱国情感。