带降维观测器的状态反馈系统

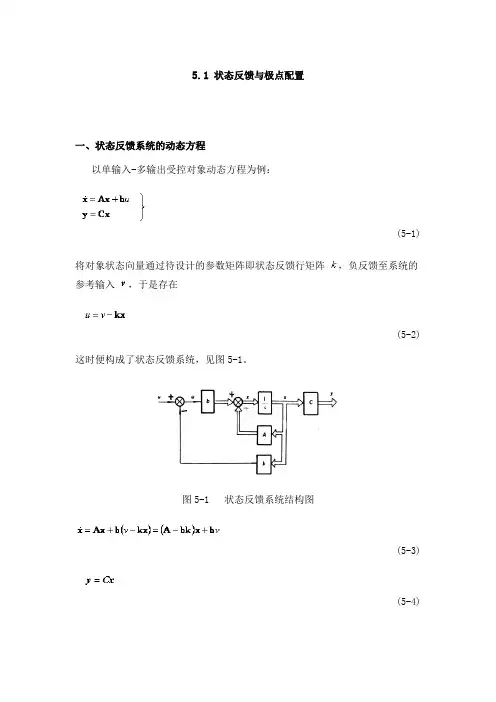
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例：(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵，负反馈至系统的参考输入，于是存在(5-2)这时便构成了状态反馈系统，见图5-1。

图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量，为维向量，为维矩阵，为维向量，为维行矩阵，为维向量，为维矩阵。

为闭环状态阵，为闭环特征多项式。

二、用状态反馈使闭环极点配置在任意位置上的充要条件是：受控对象能控证明若式(5-1)所示对象可控，定可通过变换化为能控标准形，有若在变换后的状态空间内引维状态反馈矩阵：(5-5)其中分别为由状态变量引出的反馈系数，则变换后的状态反馈系统动态方程为：(5-6)(5-7)式中(5-8)该式与仍为能控标准形，故引入状态反馈后，系统能控性不变。

特征方程为：(5-9)显见，任意选择阵的个元素，可使特征方程的个系数满足规定要求，能保证特征值（即闭环极点）任意配置。

将逆变换代入式(5-6)，可求出原状态空间内的状态反馈系统状态方程：(5-10)与式(5-3)相比，式(5-10)所示对象应引入状态反馈阵为：(5-11)需指出，当受控对象可控时，若不具有能控标准形形式，并不必象如上证明那样去化为能控标准形，只要直接计算状态反馈系统闭环特征多项式，这时，其系数为的函数，与给定极点的特征多项式系数相比较，便可确定。

能控的多输入-多输出系统，经如上类似分析可知，实现闭环极点任意配置的状态反馈阵K为维。

若受控对象不稳定，只要有能控性，完全可由状态反馈配置极点使系统稳定。

状态变量受控情况下，引入状态反馈表示增加一条反馈通路，它能改变反馈所包围环节的传递特性，即通过改变局部回路的极点来改变闭环极点配置。

不能控状态变量与控制量无关，即使引入状态反馈，对闭环极点位置也不会产生任何影响，这是因为传递函数只与系统能控、能观测部分有关的缘故。

若不能控状态变量是稳定的状态变量，那么系统还是能稳定的，否则，系统不稳定。

状态观测器摘要观测器在控制理论中非常重要。

当状态不能观测时,应设计状态观测器来估计状态。

理论分析和数值仿真证实了用所设计的观测器来估计状态的有效性。

关键字：观测器;状态观测器;设计一 全维状态观测器的设计极点配置是基于状态反馈,因此状态X 必须可观测。

当状态不能观测时,则应设计状态观测器来估计状态。

x A x B u y C x =+⎧⎨=⎩（1） 若系统完全能观测,则可构造如图1所示的状态观测器。

由上图可得观测器的状态方程为ˆˆˆxA xB u LC x L y =+-+ （2） 即 ˆˆ x (A L C )x B u L y =-++ 其特征多项式为()()f s sI A L C =--由于工程上要求ˆ x能比较快速的逼近 x ，只要调整反 馈矩阵 L, 观测器的极点就可以 任意配置达到要求的性能。

假定单变量所要求的 n 个 观测器的极点为:123.................n λλλλ , 则可求出期望的状态观测器的特征方程为:112()( n n nn n f s s a s a λλλλλλ-=---=++这时可求得反馈矩阵 L 为：10()...1o o L f A V -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ （3） 式中1...o n C C A V C A -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是将系统期望的观测器特征方程中 S 换成系统矩阵 A后的矩阵多项式。

利用对偶原则, 可使设计问题大为简化, 求解过程如下：( 1)构造系统式( 1)的对偶系统T TT z A z C B z ηω⎧=+⎪⎨=⎪⎩ （4） ( 2)用MATLAB 的函数 p l ace ( )及 acker ( ), 根据下式可求得状态观测器的反馈矩阵Lk e r(,,)T T T L a c A C P =或(,,)T T TL p la c e A C P = （5） 其中, P 为给定的极点, L 为状态观测器的反馈矩阵。

2008级综合大题[]400102110010112x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦=1 能否通过状态反馈设计将系统特征值配置到平面任意位置？2 控规范分解求上述方程的不可简约形式？3 求方程的传递函数；4 验证系统是否渐近稳定、BIBO 稳定、李氏稳定；5 可能通过状态反馈将不可简约方程特征值配置到-2，-3？若能，确定K ，若不能，请说明理由；6 能否为系统不可简约方程设计全阶状态观测器，使其特征值为-4，-5； 7画出不可简约方程带有状态观测器的状态反馈系统结构图。

参考解答： 1.判断能控性：能控矩阵21416124,() 2.000M BABA B rank M ⎡⎤⎢⎥⎡⎤==-=⎣⎦⎢⎥⎢⎥⎣⎦系统不完全可控，不能任意配置极点。

2按可控规范型分解取M 的前两列，并加1与其线性无关列构成1140120001P -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，求得1203311066001P ⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦进行变换[]1120831112,0,22260001A PAP B PB c cP --⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=-====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦ 所以系统不可简约实现为[]08112022x x u y x ⎧⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎨⎣⎦⎣⎦⎪=⎩3.12(1)(1)2(1)()()(4)(2)(1)(4)(2)s s s G s c sI A B s s s s s --+-=-==-++-+ 4.det()(4)(2)(1)sI A s s s -=-++，系统有一极点4，位于复平面的右部，故不是渐近稳定。

12(1)()()(4)(2)s G s c sI A B s s --=-=-+，极点为4，-2，存在位于右半平面的极点，故系统不是BIBO 稳定。

系统发散，不是李氏稳定。

5.可以。

令11228,12Tk k k k A Bk k +⎡⎤⎡⎤=+=⎢⎥⎢⎥⎣⎦⎣⎦则特征方程[]2112()det ()(2)28f s sI A Bk s k s k k =-+=-++--期望特征方程*2()(2)(3)56f s s s s s =++=++比较上两式求得：728Tk -⎡⎤=⎢⎥-⎣⎦6.可以。

线性系统理论的实验作业:1.找一个3阶单输入单输出系统；2.设计降维观测器（极点自己选）；3.设计带降维观测器的状态反馈系统；4.讨论降维观测器极点配置和状态反馈极点的关系；5.画出状态变量及观测误差曲线。

一．给定系统u x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=011131413121211444x .[]x y 111=1.设计一个降维观测器使其极点为-3，-4.2.设计带观测器的状态反馈系统，使其极点为-1+j2,-1. 3.讨论降维观测器的极点和状态反馈极点的关系。

4.画出状态变量及观测误差随时间变化的曲线。

解：（1）构造坐标变换矩阵。

P=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡100010111L C [] 100010111 2 11Q Q Q P =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==-用线性变换PX =x —将系统变换成∑⎪⎪⎭⎫⎝⎛C BA ___,其中 []001C 010 01131111106 =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----==-B P PA A 对于本例而言，降维观测器的的维数为n-p=2降维观测器期望特征多项式为127)4)(3()(f 2++=++=λλλλλ。

引入反馈阵⎥⎥⎦⎤⎢⎢⎣⎡=g gG 21__—得到降维观测器的特征多项式为g g 21211-1g --++λλ）（—比较两个多项式得：6g2 51-=-=g 可以得到降维观测方程：y6-5- 2u01-y 5460 6-16-1- ^^.^^⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=ωωωx 。

（为可以测量的，因为这里的的观测值或者是估计值为x1x2 2^x ）执行以下的m 文件 >> A11=6;A22=[-1,-1;1,0]; A12=[0,-1]; A21=[-11;-13]; B1=0; B2=[-1;0]; V=[-3,-4];G=(acker(A22',A12',V))' Ahat=A22-L*A12Bhat=Ahat*G+A21-G*A11 Fhat=B2-G*B1 G =-5 -6Ahat =-1 -6 1 -6Bhat =60 54Fhat =-1 0因此降解观测器的增益矩阵G=⎥⎦⎤⎢⎣⎡--65，具有期望极点的降阶观测器为 y6-5- 2u01-y 5460 6-16-1- ^^.^^⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=ωωωx 。

状态反馈与状态观测器实验状态反馈与状态观测器一、实验目的1．自学全系列状态意见反馈布局极点的方法。

2．自学降维状态观测器的设计方法。

3．学习带有状态观测器的状态反馈系统的设计方法。

二、实验仪器1．el-at-ii型自动控制系统实验箱一台2．计算机一台三、实验建议1．1）用全状态反馈配置极点的方法，按给定的性能指标进行综合设计。

2）检验极点布局理论的正确性。

2.设计一个带有状态观测器的状态反馈系统。

四、实验前分析排序和设计已知被控系统如图所示：u10.05s+1x210.1sx1y图5-1被控系统结构图1、设计一个全状态反馈系统，闭环系统性能要求为ξ=0.707，ts≤0.2s.设计k阵，并图画出来尖萼电路图挑选适当元件参数。

2、假设x２不能直接测量，设计一个降维状态观测器将x２进行估计得到估计值，然后用2形成全系列状态意见反馈，并使闭环系统ξ=0.707，ts≤0.2s，并图画出来尖萼电路图挑选x1和x独以适当元件参数。

100k50k1uf1ufda1100k25k2-out650k2-out63100k+3+x2100k2-out6x1ad131k100k0-6out+321k0+1k100k01k0图5-2状态反馈系统演示电路图图5-3带有状态观测器的状态反馈系统模拟电路图五、实验步骤1.连接被测量典型环节的模拟电路。

电路的输入u1接a/d、d/a卡的da1输出，电路的输入u2接a/d、d/a卡的ad1输出。

检查有误后拨打电源。

2.启动计算机，在桌面双击图标[自动控制实验系统]运转软件。

3.测试计算机与实验箱的通信是否正常,通信正常继续。

如通信不正常查找原因使通信正常后才可以继续进行实验。

4.在实验课题下拉菜单中挑选实验二[二阶系统阶跃积极响应],具有状态观测器的状态反馈系统挑选实验五[状态意见反馈与状态观测器]，鼠标单击该选项弹头出来实验课题参数窗口。

5.观测表明的波形记录最小市场汇率量mp和调节时间ts的数值和积极响应动态曲线，并与理论值比较。