《一类恒成立、存在性函数问题的化归》教学设计

校本资源作业高三二轮复习专题——恒成立与存在性问题在代数综合问题中常遇到恒成立与存在性问题．两类问题类似，均涉及常见函数的性质、图象，渗透着换元、化归、数形结合、函数与方程等思想方法．教学目标：1.知识与技能：理解并区别恒成立问题、存在性问题，学生能用最值和值域解决简单的恒成立和存在性问题2.过程与方法：从例题探讨恒成立、存在性问题，总结并分析数学中的恒成立和存在性问题的区别和解题规律。

培养学生的观察、分析、转化的能力3.情感态度与价值观：通过本节学习让学生体会化归转化的数学思想，享受数学中的灵动与和谐之美教学重点：对不同题型能熟练地转化为不同的最值和值域问题教学难点：化归思想的灵活运用教学过程：知识点总结：(1)恒成立问题1. ∀x∈D,均有f(x)>A恒成立，则f(x)min>A；2. ∀x∈D,均有f(x)﹤A恒成立，则f(x)ma x<A.3. ∀x∈D,均有f(x) >g(x)恒成立，则F(x)=f(x)- g(x) >0，∴F(x)min >04. ∀x∈D,均有f(x)﹤g(x)恒成立，则F(x)=f(x)- g(x) ﹤0，∴F(x) ma x﹤05. ∀x1∈D, ∀x2∈E,均有f(x1) >g(x2)恒成立，则f(x)min> g(x)ma x6. ∀x1∈D, ∀x2∈E,均有f(x1) <g(x2)恒成立，则f(x) ma x < g(x) min(2)存在性问题1. ∃x0∈D,使得f(x0)>A成立，则f(x) ma x >A；2. ∃x0∈D,使得f(x0)﹤A成立，则f(x) min <A3. ∃x0∈D,使得f(x0) >g(x0)成立，设F(x)=f(x)- g(x)，∴F(x) ma x >04. ∃x0∈D,使得f(x0) <g(x0)成立，设F(x)=f(x)- g(x)，∴F(x) min <05. ∃x1∈D, ∃x2∈E, 使得f(x1) >g(x2)成立，则f(x) ma x > g(x) min6. ∃x1∈D, ∃x2∈E,均使得f(x1) <g(x2)成立，则f(x) min < g(x) ma x(3)相等问题1. ∀x1∈D, ∃x2∈E,使得f(x1)=g(x2)成立，则{ f(x)}{g(x)}(4)恒成立与存在性的综合性问题1. ∀x1∈D, ∃x2∈E, 使得f(x1) >g(x2)成立，则f(x)m in>g(x)m in2. ∀x1∈D, ∃x2∈E, 使得f(x1) <g(x2)成立，则f(x)max <g(x)max(5)恰成立问题1. 若不等式f(x)>A在区间D上恰成立，则等价于不等式f(x)>A的解集为D；2.若不等式f(x)<B在区间D上恰成立，则等价于不等式f(x)<B的解集为D.► 探究点一 ∀x ∈D ，f (x )>g (x )的研究例1、已知函数12)(2+-=ax x x f ，xax g =)(，其中0>a ，0≠x ． 对任意]2,1[∈x ，都有)()(x g x f >恒成立，求实数a 的取值范围；【思路分析】等价转化为函数0)()(>-x g x f 恒成立，通过分离变量，创设新函数求最值解决．简解：（1）由12012232++<⇒>-+-x x x a x a ax x 成立，只需满足12)(23++=x xx x ϕ的最小值大于a 即可．对12)(23++=x x x x ϕ求导，0)12(12)(2224>+++='x x x x ϕ，故)(x ϕ在]2,1[∈x 是增函数，32)1()(min ==ϕϕx ，所以a 的取值范围是320<<a ．► 探究点二 ∃x ∈D ，f (x )>g (x )的研究对于∃x ∈D ，f (x )>g (x )的研究，先设h (x )＝f (x )－g (x )，再等价为∃x ∈D ，h (x )max >0，其中若g (x )＝c ，则等价为∃x ∈D ，f (x )max >c . 例 已知函数f (x )＝x 3－ax 2＋10.(1)当a ＝1时，求曲线y ＝f (x )在点(2，f (2))处的切线方程；(2)在区间[1,2]内至少存在一个实数x ，使得f (x )<0成立，求实数a 的取值范围． 【解答】 (1)当a ＝1时，f ′(x )＝3x 2－2x ，f (2)＝14， 曲线y ＝f (x )在点(2，f (2))处的切线斜率k ＝f ′(2)＝8， 所以曲线y ＝f (x )在点(2，f (x ))处的切线方程为 8x －y －2＝0.(2)解法一：f ′(x )＝3x 2－2ax ＝3x⎝⎛⎭⎫x －23a (1≤x ≤2)， 当23a ≤1，即a ≤32时，f ′(x )≥0，f (x )在[1,2]上为增函数， 故f (x )m in ＝f (1)＝11－a ，所以11－a <0，a >11，这与a ≤32矛盾． 当1<23a <2，即32<a <3时，当1≤x <23a ，f ′(x )<0；当23a <x ≤2，f ′(x )>0， 所以x ＝23a 时，f (x )取最小值，因此有f ⎝⎛⎭⎫23a <0，即827a 3－49a 3＋10＝－427a 3＋10<0，解得a >3352，这与32<a <3矛盾；当23a ≥2，即a ≥3时，f ′(x )≤0，f (x )在[1,2]上为减函数，所以f (x )m in ＝f (2)＝18－4a ，所以18－4a <0，解得a >92，这符合a ≥3. 综上所述，a 的取值范围为a >92. 解法二：由已知得：a >x 3＋10x 2＝x ＋10x 2， 设g (x )＝x ＋10x 2(1≤x ≤2)，g ′(x )＝1－20x 3，∵1≤x ≤2，∴g ′(x )<0，所以g (x )在[1,2]上是减函数． g (x )m in ＝g (2)，所以a >92.【点评】 解法一在处理时，需要用分类讨论的方法，讨论的关键是极值点与区间[1,2]的关系；解法二是用的参数分离，由于ax 2>x 3＋10中x 2∈[1,4]，所以可以进行参数分离，而无需要分类讨论．► 探究点三 ∀x 1∈D ，∀x 2∈D ，f (x 1)>g (x 2)的研究 例、设函数b x x a x h ++=)(，对任意]2,21[∈a ，都有10)(≤x h 在]1,41[∈x 恒成立，求实数b 的取值范围．思路分析：解决双参数问题一般是先解决一个参数，再处理另一个参数．以本题为例，实质还是通过函数求最值解决．方法1：化归最值，10)(10)(max ≤⇔≤x h x h ；方法2：变量分离，)(10x x ab +-≤或x b x a )10(2-+-≤； 方法3：变更主元，0101)(≤-++⋅=b x a x a ϕ，]2,21[∈a简解：方法1:对b x x a b x x g x h ++=++=)()(求导，22))((1)(xa x a x x a x h +-=-='， 由此可知，)(x h 在]1,41[上的最大值为)41(h 与)1(h 中的较大者．⎪⎩⎪⎨⎧-≤-≤⇒⎪⎩⎪⎨⎧≤++≤++⇒⎪⎩⎪⎨⎧≤≤∴a b a b b a b a h h 944391011041410)1(10)41(，对于任意]2,21[∈a ，得b 的取值范围是47≤b ．► 探究点四 ∀x 1∈D ，∃x 2∈D ，f (x 1)>g (x 2)的研究对于∀x 1∈D ，∃x 2∈D ，f (x 1)>g (x 2)的研究，第一步先转化为∃x 2∈D ，f (x 1)m in >g (x 2)，再将该问题按照探究点一转化为f (x 1)m in >g (x 2)m in .例、已知函数f (x )＝2|x －m |和函数g (x )＝x |x －m |＋2m －8.(1)若方程f (x )＝2|m |在[－4，＋∞)上恒有惟一解，求实数m 的取值范围； (2)若对任意x 1∈(－∞，4]，均存在x 2∈[4，＋∞)， 使得f (x 1)>g (x 2)成立，求实数m 的取值范围．【解答】 (1)由f (x )＝2|m |在x ∈[－4，＋∞)上恒有惟一解， 得|x －m |＝|m |在x ∈[－4，＋∞)上恒有惟一解．当x －m ＝m 时，得x ＝2m ，则2m ＝0或2m <－4， 即m <－2或m ＝0.综上，m 的取值范围是m <－2或m ＝0.(2)f (x )＝⎩⎪⎨⎪⎧2x －m x ≥m ，2m －xx <m ，原命题等价为f (x 1)m in >g (x 2)m in .①当4≤m ≤8时，f (x )在(－∞，4]上单调递减，故f (x )≥f (4)＝2m －4，g (x )在[4，m ]上单调递减，[m ，＋∞)上单调递增，故g (x )≥g (m )＝2m －8，所以2m －4>2m －8，解得4<m <5或m >6. 所以4<m <5或6<m ≤8.②当m >8时，f (x )在(－∞，4]上单调递减，故f (x )≥f (4)＝2m －4，g (x )在⎣⎡⎦⎤4，m 2单调递增，⎣⎡⎦⎤m 2，m上单调递减，[m ，＋∞)上单调递增，g (4)＝6m －24>g (m )＝2m －8，故g (x )≥g (m )＝2m －8，所以2m －4>2m －8， 解得4<m <5或m >6.所以m >8.③0<m <4时，f (x )在(－∞，m ]上单调递减，[m ,4]上单调递增， 故f (x )≥f (m )＝1.g (x )在[4，＋∞)上单调递增， 故g (x )≥g (4)＝8－2m ，所以8－2m <1，即72<m <4.④m ≤0时，f (x )在(－∞，m ]上单调递减，[m ,4]上单调递增， 故f (x )≥f (m )＝1.g (x )在[4，＋∞)上单调递增，故g (x )≥g (4)＝8－2m ，所以8－2m <1，即m >72(舍去)．综上，m 的取值范围是⎝⎛⎭⎫72，5∪(6，＋∞)． 【点评】 因为对于∀x ∈D ，f (x )>c ，可以转化为f (x )m in >c ；∃x ∈D ，c >g (x )，可以转化为c >g (x )m in ，所以本问题类型可以分两步处理，转化为f (x )m in >g (x )m in .► 探究点五 ∀x 1∈D ，∃x 2∈D ，f (x 1)＝g (x 2)的研究对于∀x 1∈D ，∃x 2∈D ，f (x 1)＝g (x 2)的研究，若函数f (x )的值域为C 1，函数g (x )的值域为C 2，则该问题等价为C 1⊆C 2.例、设函数f (x )＝－13x 3－13x 2＋53x －4.(1)求f (x )的单调区间； (2)设a ≥1，函数g (x )＝x 3－3a 2x －2a .若对于任意x 1∈[0,1]，总存在x 0∈[0,1]，使得f (x 1)＝g (x 0)成立，求a 的取值范围．【解答】 (1)f ′(x )＝－x 2－23x ＋53，令f ′(x )>0，即x 2＋23x －53<0，解得－53<x <1，∴f (x )的单调增区间为⎝⎛⎭⎫－53，1；单调减区间为⎝⎛⎭⎫－∞，－53和(1，＋∞)．(2)由(1)可知：当x ∈[0,1]时，f (x )单调递增，∴当x ∈[0,1]时，f (x )∈[f (0)，f (1)]，即f (x )∈[－4，－3]．又g ′(x )＝3x 2－3a 2，且a ≥1，∴当x ∈[0,1]时，g ′(x )≤0，g (x )单调递减，∴当x ∈[0,1]时，g (x )∈[g (1)，g (0)]，即g (x )∈[－3a 2－2a ＋1，－2a ]，又对于任意x 1∈[0,1]，总存在x 0∈[0,1]，使得f (x 1)＝g (x 0)成立⇔[－4，－3]⊆[－3a 2－2a ＋1，－2a ]，即⎩⎪⎨⎪⎧－3a 2－2a ＋1≤－4，－3≤－2a ，解得1≤a ≤32.恒成立与存在有解的区别：恒成立和有解是有明显区别的，以下充要条件应细心思考，甄别差异，恰当使用，等价转化，切不可混为一体。

(完整版)高一数学函数和不等式中恒成立问题的教案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)高一数学函数和不等式中恒成立问题的教案）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)高一数学函数和不等式中恒成立问题的教案的全部内容。

（完整版)高一数学函数和不等式中恒成立问题的教案编辑整理:张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是我们任然希望 (完整版）高一数学函数和不等式中恒成立问题的教案这篇文档能够给您的工作和学习带来便利。

同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为〈(完整版）高一数学函数和不等式中恒成立问题的教案> 这篇文档的全部内容。

函数和不等式结的恒成立问题的解法“含参不等式恒成立问题”把不等式、函数、三角、几何等内容有机地结合起来，其以覆盖知识点多，综合性强,解法灵活等特点而倍受高考、竞赛命题者的青睐。

另一方面，在解决这类问题的过程中涉及的“函数与方程”、“化归与转化”、“数形结合”、“分类讨论”等数学思想对锻炼学生的综合解题能力,培养其思维的灵活性、创造性都有着独到的作用恒成立问题的基本类型：一、判别式法若所求问题可转化为二次不等式,则可考虑应用判别式法解题。

一般地,对于二次函数),0()(2R x a c bx ax x f ∈≠++=，有1）0)(>x f 对R x ∈恒成立⎩⎨⎧<∆>⇔00a ； 2）0)(<x f 对R x ∈恒成立.00⎩⎨⎧<∆<⇔a 例1:若不等式02)1()1(2>+-+-x m x m 的解集是R ，求m 的范围。

不等式专题复习不等式恒成立和存在性问题教学设计一、教学目标确立依据（一）课程标准要求及解读1.课程标准要求（1）经历从实际情境中中抽象出一元二次不等式模型的过程；（2）通过函数图形了解一元二次不等式与相应函数、方程的关系（3）会用基本不等式解决简单的最大（小）值问题2.课程标准解读（1）不等式的考查主要以中档题为主，以选填题为主；（2）不等式的性质常与简易逻辑结合考查；（3）不等式的解法主要以一元二次不等式为主，兼顾其它（如简单的分式不等式、绝对值不等式、指对数不等式、与分段函数有关的不等式等），常与集合（选填题）、导数（解答题中对参数的分类讨论）结合；（4）线性规划问题难度不大；（5）基本不等式求最值是重点，要加强训练；（6）不等式的恒成立也应当重视。

（二）教材分析本章的主要内容是：不等式的性质、不等式的证明和一些简单不等式的解法；其中不等式的证明和不等式的解法是重点；不等式的性质及其证明中，不等式的证明是难点，掌握不等式的性质是学好本章的关键。

本节课的重点是不等式恒成立问题的探究，难点是用求函数（表达式）最值（取值范围）解决恒成立问题（三）学情分析1．认知分析：学生在初中已经学习了一元二次方程和二次函数，对不等式的性质有了初步的了解，在高中也学习了基本不等式，这为我们学习恒成立转化为函数（或二元变量）求最值打下了基础。

2．能力分析：高中学段的学生数学思维较初中来说更为严密，抽象思维能力也有了进一步的提升。

3．情感分析：学生对高考重点内容的学习有一定的兴趣和积极性，但在探究问题的能力以及合作交流等方面的发展不够均衡。

因此对于这个阶段的学生来说，对恒成立的学习有一定的基础和必要。

二、教学目标目标1：通过独立思考完成典型例题，梳理构建解题方法、解题步骤和注意问题，培养直观想象、逻辑推理、数学运算和数学抽象的核心素养目标2：通过小组合作探究完成变式练习，掌握不同的数学问题与不等式恒成立和存在性问题之间的等价转化，培养逻辑推理的核心素养目标3：通过独立思考完成目标检测，合理选择解决问题的方法，培养逻辑推理和数学运算的核心素养.三、评价设计目标1评价：学生通过独立思考，都能用基本三种方法中的一种解决简单的恒成立问题过程；目标2评价：通过小组讨论后的抢答展示，都能注意处理恒成立问题的细节目标3评价：学生通过独立思考，完成目标检测，60%的学生能正确解答，40%的学生通过学生讲解能意识到自己的错误并改正；四、教学过程一、“做”中“理”——问题导入，梳理知识师：通过前面的学习，发现同学们对不等式恒成立问题还存在思路不清晰，方法选择不恰当的情况。

等差数列--整节课例_高中数学广东名师课堂教学展示视频等差数列的前n项和--整节课例_高中数学广东名师课堂教学展示视频函数的思想--整节课例_高中数学广东名师课堂教学展示视频排列——求解有限制条件的排列问题的常用方法--整节课例_高中数学广东名师课堂教学展示视频观通项定类型巧放缩--整节课例_高中数学广东名师课堂教学展示视频基本不等式--整节课例_高中数学广东名师课堂教学展示视频函数与方程--整节课例_高中数学广东名师课堂教学展示视频排列组合之均匀分配问题--整节课例_高中数学广东名师课堂教学展示视频函数的极值与导数--整节课例_高中数学广东名师课堂教学展示视频求三角函数最值的方法--整节课例_高中数学广东名师课堂教学展示视频等比数列--整节课例_高中数学广东名师课堂教学展示视频数形结合--整节课例_高中数学广东名师课堂教学展示视频空间元素的平行关系--整节课例_高中数学广东名师课堂教学展示视频求函数的解析式--整节课例_高中数学广东名师课堂教学展示视频函数思想---不等式--整节课例_高中数学广东名师课堂教学展示视频余弦定理--整节课例_高中数学广东名师课堂教学展示视频平面向量的数量积--整节课例_高中数学广东名师课堂教学展示视频正态分布--整节课例_高中数学广东名师课堂教学展示视频直线的参数方程--整节课例_高中数学广东名师课堂教学展示视频平面向量的数量积--整节课例(1)_高中数学广东名师课堂教学展示视频椭圆和双曲线的构造实验--整节课例_高中数学广东名师课堂教学展示视频随机事件的概率--整节课例_高中数学广东名师课堂教学展示视频直线与圆锥曲线的位置关系--整节课例_高中数学广东名师课堂教学展示视频函数的单调性与导数--整节课例_高中数学广东名师课堂教学展示视频椭圆--整节课例_高中数学广东名师课堂教学展示视频直线与平面垂直的判定--整节课例_高中数学广东名师课堂教学展示视频正态分布习题课人教版复习课高三数学优秀课展示实录视频抛物线的标准方程苏教版选修庄素娟高三数学优秀课展示实录视频正态分布习题课人教版高三数学优秀课展示实录视频正态分布人教版高三数学优秀课展示实录视频园锥曲线的统一定义苏教版选修教材高三数学优秀课展示实录视频圆锥曲线的共性探究人教版高三数学优秀课展示实录视频直线与平面垂直的判定人教版高三数学优秀课展示实录视频复数的几何意义苏教版高三数学优秀课展示实录视频函数的图像北师大版舒焰高三数学优秀课展示实录视频正态分布高三数学优秀课展示实录视频椭圆的简单几何性质人教版高三数学优秀课展示实录视频几种常见函数的导数人教版高三数学优秀课展示实录视频直线与双曲线的位置关系人教版高三数学优秀课展示实录视频抛物线性质人教版高三数学优秀课展示实录视频椭圆及其标准方程二（复习）人教版高三数学优秀课展示实录视频导数及其应用苏教版高三数学优秀课展示实录视频椭圆及其标准方程人教版高三数学优秀课展示实录视频等差数列复习课苏教版高三数学优秀课展示实录视频函数的奇偶性人教版高三数学优秀课展示实录视频里程碑上的数北师大版_高一数学优质课实录展示视频等比数列北师大版高三数学优秀课展示实录视频等差等比数列的运用人教版高三数学优秀课展示实录视频中位数和众数郭爱玲_高一数学优质课实录展示视频空间线面的位置关系数学必修2_高一数学优质课实录展示视频平面与平面平行的判定人教版高一数学优秀课展示实录视频向量的运算人教版高一数学优秀课展示实录视频探索三角形相似的条件北师大版_高一数学优质课实录展示视频(1)探索多边形的内角和北师大版_高一数学优质课实录展示视频谁的包裹多北师大版_高一数学优质课实录展示视频余弦定理高中数学必修5_高一数学优质课实录展示视频求最大公约数人教版高一数学优秀课展示实录视频求函数的解析式人教版高一数学优秀课展示实录视频二元一次方程组(第一课时) 北师大版_高一数学优质课实录展示视频函数的奇偶性数学（上册）_高一数学优质课实录展示视频梯形北师大版_高一数学优质课实录展示视频直线与平面垂直的判定人教版高一数学优秀课展示实录视频变化的“鱼” 北师大版_高一数学优质课实录展示视频古典概型人教版高一数学优秀课展示实录视频面面平行性质定理苏教版《必修2》高一数学优秀课展示实录视频素质_高一数学优质课实录展示视频生活中的平移北师大版_高一数学优质课实录展示视频图案欣赏与设计人教版高一数学优秀课展示实录视频选择结构人教版高一数学优秀课展示实录视频线性回归方程人教版_高一数学优质课实录展示视频加减法解二元一次方程组北师大版_高一数学优质课实录展示视频利用表格分析不等式组应用题北师大版_高一数学优质课实录展示视频指数函数及其性质（1）人教版 a版_高一数学优质课实录展示视频向量数乘运算及期几何意义人教版高一数学优秀课展示实录视频一元二次不等式数学基础模块_高一数学优质课实录展示视频整式的运算复习二北师大版_高一数学优质课实录展示视频形状相同的图形北师大版_高一数学优质课实录展示视频函数的单调性和导数人教版_高一数学优质课实录展示视频任意角的三角涵数高教版_高一数学优质课实录展示视频谁的包裹多北师大版(1)_高一数学优质课实录展示视频数列求和的常用方法人教版职高基础模块（下）_高一数学优质课实录展示视频中位数和众数北师大版_高一数学优质课实录展示视频平面向量的数量积苏教版高一数学优秀课展示实录视频函数的单调性人教a版_高一数学优质课实录展示视频直线与平面平行的判定人教版高一数学优秀课展示实录视频探索勾股定理北师大版_高一数学优质课实录展示视频归纳法人教版高一数学优秀课展示实录视频点斜式方程_高一数学优质课实录展示视频中心投影与平等投影空间几何体的三视图人教版_高一数学优质课实录展示视频等比数列前n项和新人教版_高一数学优质课实录展示视频函数的单调性全国中职数学_高一数学优质课实录展示视频直线与平面垂直的判定人教版_高一数学优质课实录展示视频指数函数苏教版_高一数学优质课实录展示视频探索三角形相似的条件北师大版_高一数学优质课实录展示视频0074张广平_线面平行的判定0072李启龙_直线与平面平行的性质0074唐雪莲_由立体图形到视图(1)0072高二数学公开课多面体欧拉定理0074唐雪莲_由立体图形到视图0071陈颈彬_系统抽样0074椭圆与双曲线的构造实验(信息技术与学科整合)0072函数的建模与应用吴万辉_不等式的证明(两课时)2丁益祥_等差数列(两课时)20074吴立波_画立体图形吴万辉_不等式的证明(两课时)1游戏公平吗丁益祥_等差数列(两课时)1设计遮阳蓬椭圆与它的标准方程圆的参数方程简单的图案设计三角函数的图像与性质抛物线的简单几何性质对数导数等可能性事件的概率等差数列01等差数列02函数图像的四类变换分类讨论思想(高中)计数基本原理(职教数学)抽样调查举例函数的再值互斥事件有一个发生的概率立体图形与平面图形函数的应用平移高三数学复习课数学：圆形统计图数列复习等差数列（高三）函数的复习（高三）圆的标准方程（高二）椭圆的定义及其标准方程（高二）生活中的数学一元二次不等式图解虚根函数的单调性集合抛物线及其标准方程二次函数yax2bxc的图象1二次函数yax2bxc的图象2球的体积课堂实录四二次函数yax2的图象2二次函数yax2的图象1球的体积课堂实录三球的体积课堂实录五球的体积课堂实录二球的概念和性质课堂实录三球的概念和性质教学设计球的体积课堂实录一函数yasin(ωχφ）的图象4球的概念和性质课堂实录二函数yasin(ωχφ）的图象1球的概念和性质课堂实录一函数yasin(ωχφ）的图象3函数yasin(ωχφ）的图象2高三数学优质课展示《等差等比数列的运用》人教版_陆老师高三数学优质课视频《试卷分析》研究课_李世强高一数学优质课视频《任意角》人教版_王老师高一高中数学优质示范课视频《函数的单调性》1高一高中数学优质示范课视频《函数的单调性》2高一高中数学优质示范课视频《平面向量数量积的坐标表示》高一高中数学优质示范课视频《平面向量》高一高中数学优质示范课视频《平移_习题课》高一高中数学优质示范课视频《一类恒成立、存在性函数问题的化归》课堂实录高一高中数学优质示范课视频《一元二次方程根的分布（一）》_陈永胜高一数学优质课视频《正余弦函数周期性》高中数学优质课视频《方程的根与函数的零点》44中学王璐璐高中数学优质课视频《三角函数的诱导公式》工大附中李静高中数学优质课视频《三角函数的诱导公式》中实学校赵立娟高中数学优质课视频《三角函数的诱导公式》13中学贾功亮高中数学优质课视频《三角函数的诱导公式》37中学张巍高二高中数学优质课视频《椭圆的标准方程》丁老师_江苏省高中青年教师优质课观摩高二高中数学优质课视频《椭圆的标准方程》陈老师_江苏省高中青年教师优质课观摩高二高中数学优质课视频《椭圆的标准方程》翟老师_江苏省高中青年教师优质课观摩高二高中数学优质课视频《椭圆的标准方程》赵老师_江苏省高中青年教师优质课观摩高二高中数学优质课视频《椭圆的标准方程》方老师_江苏省高中青年教师优质课观摩高二高中数学优质课视频《椭圆的标准方程》邱老师_江苏省高中青年教师优质课观摩高二高中数学优质课视频选修2《平均变化率》董老师_江苏省高中青年数学教师优秀课观摩与评比活动高二高中数学优质课展《导数在研究函数中的应用》高二高中数学优质示范课《双曲线的第二定义》_文静妍高二高中数学优质课视频选修2《平均变化率》杜老师_江苏省高中青年数学教师优秀课观摩与评比活动高二高中数学优质课视频选修2《平均变化率》朱老师_江苏省高中青年数学教师优秀课观摩与评比活动高二高中数学优质示范课《总体分布的估计》(1)高一高中数学优质课视频展示《函数的单调性》高老师_江苏省高中青年教师优质课观摩高三高中数学优质示范课视频《数列复习》_熊贵旭高一高中数学优质课视频展示《函数的单调性》解老师_江苏省高中青年教师优质课观摩活动高一高中数学优质课视频展示《函数的单调性》凌老师_江苏省高中青年教师优质课观摩活动高一高中数学优质课视频展示《函数的单调性》秦老师_江苏省高中青年教师优质课观摩高一高中数学优质课视频展示《函数的单调性》杨老师_江苏省高中青年教师优质课观摩活动高一高中数学优质课视频展示《函数的单调性》沈老师_江苏省高中青年教师优质课观摩高一高中数学优质课视频展示《函数的单调性》张老师_江苏省高中青年教师优质课观摩高一高中数学优质课视频展示《函数综合运用》高一高中数学优质课视频展示《空间几何体的表面积》浦老师1、函数奇偶性问题探究朱胜强3、如何研究圆锥曲线离心率的问题孔繁海2、运用同角函数之间的关系求值周德3、数列中通项与和式的关系探究易雪梅4、如何研究直线与圆锥曲线中与分线段成比例有关的问题？：孔繁海《简单的线性规划问题》优质示范课2_雷波《两个变量之间的线性相关》优质示范课1_曹慧斌《两个变量之间的线性相关》优质示范课3_曹慧斌1、如何利用导数研究“恒成立”的问题刘明2、如何用导数解决与切线有关的问题？刘明《两个变量之间的线性相关》优质示范课2_曹慧斌《两个变量之间的线性相关》优质示范课4_曹慧斌《数学归纳法》2_曾群凤优质示范课《直线的倾斜角与斜率》1吴剑松优质示范课5、如何利用从特殊到一般的思想解决数列问题杨东福6、如何从函数的角度思考数列问题杨东福优质示范课a0548高三数学讲座直线与园的位置关系a0644高三数学讲座《直线与园的位置关系》a0549高三数学讲座例说数学解题思考方法《数学归纳法》1_曾群凤优质示范课a1252第四届“南回杯”优课评比录像三《函数与方程》a1253第四届“南回杯”优课评比录像四《坐标法在解三角形中的运用》g0425高一数学优质示范课《for循环语句》_郭小喜g0425高一数学优质示范课《分段函数的探索与应用》_程伟华g0425高一数学优质示范课《三角函数的图象与性质》_陈向东g0426高一数学优质示范课《函数模型的选择与求解》_陈丹妮g0427高二数学优质示范课《空间角-线面角》_曾菲g0427高二数学优质示范课《两条平行直线和重合的条件》_路彦星g0428高二数学优质示范课《椭圆及其标准方程》_曾菲g0429高二数学优质示范课立体几何《二面角》_邹建平g0430高二数学优质示范课《算法与程序设计》_林启明g0430高二数学优质示范课《算法与程序设计》_刘琦g0431高三数学优质示范课_高三数学第二轮复习《数形结合与最值》_袁海勇g0432高三数学优质示范课《正态分布》g0433高三数学优质示范课《高中数学专题复习—分类讨论思想》_王宗祥g0433高三数学优质示范课《高中数学专题复习—分类讨论思想》专家点评《函数概念及其表示》一轮复习优质示范课g44586高一数学微课示范必修5《数学的概念及其通项》讲授类教学片段_人教版g47046高三数学优质课展示《数列中的分类讨论思想》_李老师g44622高三数学优质课展示《等差数列复习课》苏教版_熊老师g73650高一数学优质课展示《线性回归方程》人教版_冯老师h5066高二数学优质课展示《双曲线及其标准方程》_曹东辉h5063高二数学优质课展示《平面与平面垂直的性质》黄海波h5057高二数学优质课展示《从抛物线定义引出的不变性问题》h5062高二数学优质课展示《抛物线性质》_h5070高二数学优质课展示《正态分布习题课》_袁志斌h5072高三数学优质课展示《导数的应用》_俞立柱h5071高二数学优质课展示《直线与平面垂直的判定》_尹向勇h5069高二数学优质课展示《正态分布习题课》_袁扬h5074高三数学优质课展示《第二轮高考数学复习：第五讲数列极限数学归纳法》h5068高二数学优质课展示《正态分布》_袁志斌h5073高二数学优质课展示《归纳推理》_管敏慧h5076高三数学优质课展示《复数的几何意义》_陈正坤h5075高二数学优质课展示选修2《椭圆及其标准方程》_-李勇成h5082高一数学优质课展示《等差数列》_吴莫林h5083高一数学优质课展示《等差数列与等比数列的类比》实录说课h5080高三数学优质课展示《圆锥曲线的共性探究》复习课_史强h5081高一必修2数学优质课展示《直线与平面垂直》_郭长慧(一等奖)h5086高一数学优质课展示《方程的根与函数的零点》_刘成雨h5088高一数学优质课展示《归纳法》_袁志斌h5087高一数学优质课展示《古典概型》_刘强h5085高一数学优质课展示《反函数》_松江二中h5089高一数学优质课展示《函数图像变换》_汪燕h5090高一数学优质课展示《平面向量的数量》_积陆春h5092高一数学优质课展示《求函数的解析式》_金海淑h5095高一数学优质课展示《数学归纳法》_刘娟h5094高一数学优质课展示《三角函数图像性质》_王家陵h5093高一数学优质课展示《求最大公约数》_罗江云h5097高一数学优质课展示《同角三角函数的基本关系》_崔传志h5098高一数学优质课展示《图案欣赏与设计》_冯辉h5096高一数学优质课展示《数学建模论文研读》h5099高一数学优质课展示《向量的运算》_赖春雨h5100高一数学优质课展示《向量的运用》_李勇h5102高一数学优质课展示《向量数乘运算及期几何意义》_陈开金h6739高二数学优质课展《导数在研究函数中的应用》h5105高中数学优质课展示《一个最值问题的解法研究》h6740高二数学优质课展示《二面角》侯老师h6742高二数学优质课展示《两平面垂直》h5103高一数学优质课展示《选择结构》_黎永生h6744高二数学优质课展示《椭圆的标准方程》丁老师_江苏省高中青年教师优质课观摩h6743高二数学优质课展示《椭圆的标准方程》陈老师_江苏省高中青年教师优质课观摩h6745高二数学优质课展示《椭圆的标准方程》方老师_江苏省高中青年教师优质课观摩h6746高二数学优质课展示《椭圆的标准方程》蒋老师_江苏省高中青年教师优质课观摩h6747高二数学优质课展示《椭圆的标准方程》磊老师_江苏省高中青年教师优质课观摩h6748高二数学优质课展示《椭圆的标准方程》潘老师_江苏省高中青年教师优质课观摩h6749高二数学优质课展示《椭圆的标准方程》濮阳老师_江苏省高中青年教师优质课观摩h6750高二数学优质课展示《椭圆的标准方程》邱老师_江苏省高中青年教师优质课观摩h6751高二数学优质课展示《椭圆的标准方程》徐老师_江苏省高中青年教师优质课观摩h6752高二数学优质课展示《椭圆的标准方程》杨老师_江苏省高中青年教师优质课观摩h6753高二数学优质课展示《椭圆的标准方程》营老师_江苏省高中青年教师优质课观摩h6754高二数学优质课展示《椭圆的标准方程》翟老师_江苏省高中青年教师优质课观摩h6755高二数学优质课展示《椭圆的标准方程》赵老师_江苏省高中青年教师优质课观摩h6757高一数学优质课展示必修5《一元二次不等式》h6756高二数学优质课展示《椭圆上的点对两焦点张角的探究》h6758高二数学优质课展示选修2《平均变化率》曹老师_江苏省高中青年数学教师优秀课观摩与评比活动h6759高二数学优质课展示选修2《平均变化率》董老师_江苏省高中青年数学教师优秀课观摩与评比活动h6760高二数学优质课展示选修2《平均变化率》杜老师_江苏省高中青年数学教师优秀课观摩与评比活动h6763高二数学优质课展示选修2《平均变化率》侯老师_江苏省高中青年数学教师优秀课观摩与评比活动h6761高二数学优质课展示选修2《平均变化率》葛老师_江苏省高中青年数学教师优秀课观摩与评比活动h6764高二数学优质课展示选修2《平均变化率》朱老师_江苏省高中青年数学教师优秀课观摩与评比活动h6766高三数学优质课展示《空间的距离复习课》h6765高三数学优质课展示《等值线的判读与运用》h6768高一数学优质课展必修2《平面图形的翻折》h6767高三数学优质课展示《探索性问题和开放性问题》h6771高一数学优质课展示《函数的单调性》淮老师_江苏省高中青年教师优质课观摩h6773高一数学优质课展示《函数的单调性》秦老师_江苏省高中青年教师优质课观摩h6772高一数学优质课展示《函数的单调性》陆老师_江苏省高中青年教师优质课观摩h6769高一数学优质课展示《分期付款》杨老师_江苏省高中青年数学教师优秀课观摩与评比活动h6774高一数学优质课展示《函数的单调性》沈老师_江苏省高中青年教师优质课观摩h6775高一数学优质课展示《函数的单调性》水老师_江苏省高中青年教师优质课观摩h6777高一数学优质课展示《函数的单调性》张老师_江苏省高中青年教师优质课观摩h5073高三数学优质课展示《第二轮高考数学复习：第四讲复数变换专题》h6778高一数学优质课展示《函数的单调性》解老师_江苏省高中青年教师优质课观摩活动h6781高一数学优质课展示《函数的单调性》吴老师_江苏省高中青年教师优质课观摩活动h6780高一数学优质课展示《函数的单调性》陆老师_江苏省高中青年教师优质课观摩活动h6782高一数学优质课展示《函数的单调性》杨老师_江苏省高中青年教师优质课观摩活动h6776高一数学优质课展示《函数的单调性》伍老师_江苏省高中青年教师优质课观摩h6784高一数学优质课展示《函数的奇偶性》h6783高一数学优质课展示《函数的单调性》张老师_江苏省高中青年教师优质课观摩活动h6779高一数学优质课展示《函数的单调性》凌老师_江苏省高中青年教师优质课观摩活动h6788高一数学优质课展示《空间几何体的表面积》浦老师h6790高一数学优质课展示《映射的概念》钱老师h6789高一数学优质课展示《生活中的变量关系》h6791高一数学优质课展示必修3《算法的含义》唐老师h5075高三数学优质课展示《第二轮高考数学复习：第一讲函数不等式专题（上）》h7780高中数学特级教师精品示范课《复数的乘法和除法》h7781高中数学特级教师精品示范课《复数的概念》h6785高一数学优质课展示《函数综合运用》h7773高一数学优质课展示必修2《空间线面的位置关系》_陈老师h7782高中数学特级教师精品示范课《复数的加法和减法》h7783高中数学特级教师精品示范课《复数复习》h7784高中数学特级教师精品示范课《极坐标系》h7787高中数学特级教师精品示范课《圆锥曲线复习（二）》h6786高一数学优质课展示《角的概念的推广》h7788高中数学特级教师精品示范课《圆锥曲线复习（一）》h7772高一数学优质课展示《直线与平面垂直的判定》人教版_蔡老师h7792高二数学特级教师精品示范课《排列组合应用问题》h7785高中数学特级教师精品示范课《极坐标系和直角坐标的互化》h7793高二数学特级教师精品示范课《组合与组合数公式（二）》h7790高二数学特级教师精品示范课《排列组合应用问题（续）》h7786高中数学特级教师精品示范课《圆锥曲线的轨迹问题》h7799高三数学特级教师精品示范课《函数综合复习》h30081高三数学优质课展示《恒成立问题(一)》人教版_俞老师h7791高二数学特级教师精品示范课《排列组合应用问题（一）》h75147高一数学优质课展示《函数的单调性》人教a版_黎老师h75149高二数学优质课展示《等差数列求和》_黄老师h77343高一数学优质课展示《任意角的三角涵数》高教版_郑老师h75148高一数学优质课展示《指数函数及其性质（1）》人教a版_刘老师。

《利用函数性质判定方程解的存在》教学设计教材：普通高中课程标准实验教科书高中数学(北师大版)必修1第四章函数的应用一、教学目标(一)知识与技能1.结合方程解的几何意义，理解函数零点的定义；2.结合零点定义的探究，掌握方程的实数解与其相应函数零点之间的等价关系；3.结合几类基本初等函数的图象特征，掌握判断函数的零点个数和所在区间的方法.(二)过程与方法1.通过化归与转化思想的引导，培养学生从已有认知结构出发，寻求解决棘手问题方法的习惯；2.通过数形结合思想的渗透，培养学生主动应用数学思想的意识；3.通过习题与探究知识的相关性设置，引导学生深入探究得出判断函数的零点个数和所在区间的方法；4.通过对函数与方程思想的不断剖析，促进学生对知识灵活应用的能力。

(三)情感、态度与价值观1.让学生体验化归与转化、数形结合、函数与方程这三大数学思想在解决数学问题时的意义与价值；2.培养学生锲而不舍的探索精神和严密思考的良好学习习惯；3.使学生感受学习、探索发现的乐趣与成功感。

二、教学重点与难点教学重点:零点的概念及零点存在性的判定。

教学难点:探究判断函数的零点个数和所在区间的方法.三、教学的方法与手段授课类型：新授课教学方法：启发式教学、探究式学习教学辅助: 多媒体四、教学过程(一)问题引入,揭示课题1、教师：同学们回顾一下,我们初中已经学过一元一次方程、二元一次方程组、一元二次方程，并掌握了一些方程的求解公式，那么我们今天继续来讨论方程解的问题。

请同学们先来看大屏幕这个问题。

思考1：判断下列方程是否有实数解，有几个实数解？x-=2(1)10(3)60-+=(4)ln260x x--=2(2)60x x+-=x x学生活动：回答，思考解法。

教师：第四个方程若利用初中的求解方法我们难以判断！大家想一下，我们初中里面学习过函数与方程之间的关系，那么我们这节课就来学习《利用函数性质判定方程解的存在》（揭示课题）。

通过这节课的学习我们就可以解决第四个问题（揭示课题:利用函数性质判定方程解的存在）教师：我们继续来讨论思考1的这一元二次方程。

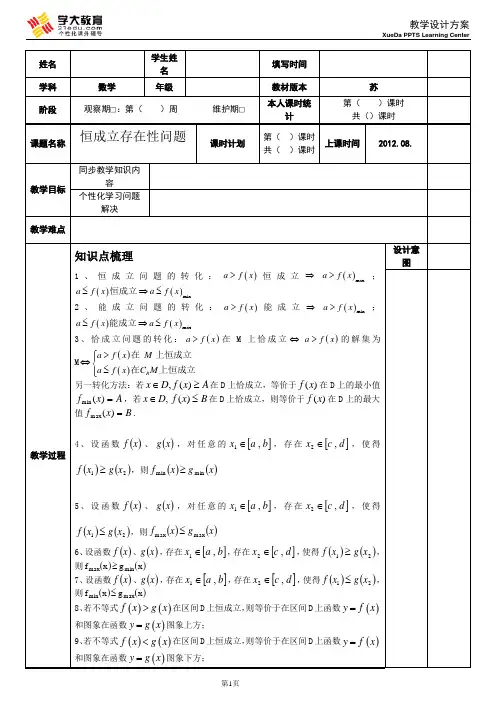
适用学科 适用区域 知识点高中数学 苏教版 1.恒成立问题 2.存在性问题适用年级 课时时长（分钟）高二 2 课时教学目标1. 能利用导数熟练解决恒成立问题 ． 2. 能利用导数熟练解决存在性问题教学重点 教学难点【知识导图】分辨恒成立问题、存在性问题 理解最大最小值成立教学过程一、导入【教学建议】 导入是一节课必备的一个环节， 是为了激发学生的学习兴趣， 帮助学生尽快进入学习状 态。

导入的方法很多，仅举两种方法： ① 情境导入，比如讲一个和本讲内容有关的生活现象； ② 温故知新，在知识体系中，从学生已有知识入手，揭示本节知识与旧知识的关系，帮学 生建立知识网络。

极值与最值的区别和联系(1)函数的极值表示函数在一点附近的情况，是在局部对函数值的比较；函数的最值是 函数在整个定义域上的情况，是对函数在整个定义域上的函数值的比较． (2)函数的极值不一定是最值，需对极值和区间端点的函数值进行比较，或者考察函数第 1 页在区间内的单调性． (3)如果连续函数在区间(a，b)内只有一个极值，那么极大值就是最大值，极小值就是最 小值． (4)可用函数的单调性求 f(x)在区间上的最值，若 f(x)在[a，b]上单调递增，则 f(x)的最大 值为 f(b)，最小值为 f(a)，若 f(x)在[a，b]上单调递减，则 f(a)为函数的最大值，f(b)为函数的 最小值．二、知识讲解（ 1）恒成立问题的转化： 考点 1 恒成立问题 a  f  x  恒成立  a  f  x max ； a  f  x  恒成立  a  f  x min （2）能成立问题的转化： a  f  x  能成立  a  f  x min ； a  f  x 能成立  a  f  x max （3）恰成立问题的转化： a  f  x  在 M 上恰成立  a  f  x  的解集为 M a  f  x  在 M 上恒成立  a  f  x  在CR M 上恒成立另一转化方法：若 x  D, f ( x)  A 在 D 上恰成立，等价于 f ( x ) 在 D 上的最小值f min ( x)  A ，若 x  D, f ( x)  B 在 D 上恰成立，则等价于 f ( x) 在 D 上的最大值f max ( x)  B .（4）若不等式 f  x   g  x  在区间 D 上恒成立，则等价于在区间 D 上函数 y  f  x  和图 象在函数 y  g  x  图象上方； （5）若不等式在区间 D 上恒成立，则等价于在区间 D 上函数 y  f  x  和图象在函数y  g  x  图象下方；考点 2 存在性问题（1）设函数 f x  、 g x  ，对任意的 x1  a , b ，存在 x 2  c , d ，使得 f x1   g x2  ， 则 f min x   g min x 第 2 页（2）设函数 f x  、 g x  ，对任意的 x1  a , b ，存在 x 2  c , d ，使得 f x1   g x2  ， 则 f max x  g max x 。

高三二轮复习专题《恒成立与存在性问题的解题策略》教学设计作者：郝松宝来源：《教育教学论坛》 2014年第47期郝松宝（河南省郑州市第二外国语学校，河南郑州450041）摘要：新课标下的高考越来越注重对学生的综合能力的考查，而“恒成立与存在性问题”便是一个考查学生综合能力的最佳途径，并逐渐成为最近几年高考的一个热点，而且其形式逐渐多样化，出现的试题大多数以综合性较强的解答题为主.因此研究此类问题的解题策略就显得尤为重要了.关键词：恒成立问题；存在性问题；函数的最值；等价转化中图分类号：G633.6 文献标志码：A 文章编号：1674-9324（2014）47-0058-03【设计理念】课标下的高考越来越注重对学生的综合能力的考查，恒成立与存在性问题便是一个考查学生综合能力的重要途径，成为近几年高考的一个热点，其形式逐渐多样化.它主要涉及函数的图象与性质，渗透着化归与转化、函数与方程、数形结合等多种数学思想与方法，在培养等学生的综合能力方面起到了重要的作用. 近三年的全国各地高考数学试卷中都出现恒成立与存在性问题，其形式逐渐多样化，但都是集中考查了函数、导数等重要知识.题型结构基本上都是以函数为载体，以导数为工具，考查函数性质及导数应用为目标，其中运用导数确定含参数函数的参数取值范围是一类常见的探索性问题中，主要是求存在性问题或恒成立问题中的参数的范围.以2013高考试卷为例，部分试卷中出现恒成立与存在性的题目如下：全国I文第24题、全国I理第21题、全国Ⅲ理第21题、辽宁理第21题、重庆理第16题等.【教学目标】知识与技能：能把恒成立与存在性问题的转化为函数最值，并掌握解决此类问题的基本方法.过程与方法：体会函数与方程思想、转化与化归思想、数形结合思想三大数学思想的应用.情感、态度与价值观：通过对恒成立与存在性问题的学习，体会普遍联系与辩证统一哲学观点，进一步激发数学学习兴趣，获取数学学习的成就感.【教学重点】理解恒成立问题与存在性问题的实质就是函数最值问题，掌握解决恒成立与存在性问题的基本方法.【教学难点】如何利用转化与化归的方法来处理恒成立与存在性问题.【教学过程】一、核心知识点梳理“恒成立”的含义，一定是比“比最大的还大”或“比最小的还小”. 因此恒成立问题往往又可以转化为求函数最值的问题.恒成立、能成立、恰成立问题的区别与联系：恒成立、能成立、恰成立问题是函数最值的所呈现的三种不同形式，例如：（x）恒成立，求实数a取值范围.（答案略）【设计意图】通过对近两年高考压轴题的练习，让学生深刻体会高考是如何考查恒成立与存在性问题的.进一步辨析恒成立、能成立、恰成立问题的区别与联系，熟练恒成立、能成立、恰成立问题解决方法.四、归纳生成恒成立、能成立、恰成立问题的区别与联系：恒成立、能成立、恰成立问题是函数最值的所呈现的三种不同形式，它们的共同点是均能等价转化为函数的最值问题.【设计意图】课堂上学生先总结，教师再点拨.帮助学生形成知识网络.五、布置作业：针对性专项练习（略）【设计意图】巩固深化所学知识.。

利用常数分离法解决一类恒成立问题教学目标：1．会求三次函数的导数，如32(0)y ax bx cx d a =+++≠，则'y = ；2．会求函数形如(0,0)b y ax a b x=+>>在给定区间上的最值； 3．会用基本不等式：(0,0)a b a b +≥>>. 教学重、难点：重点：利用常数分离法解决含一个参数的二次函数恒成立问题；难点：如何解决形如：()M f x ≤或()M f x ≥的问题.基础自测:引例.已知3211132y x ax x =-++是(0,)+∞上的单调递增函数，则a 的取值范围是（ ） .0A a < .22B a -≤≤ .2C a < .2D a ≤设置说明：(1)已知单调性可得出/0y ≥，学生的可能错误是/0y >，又/0y ≥是导函数在(0,)+∞上恒大于等于O ，也是恒成立问题）(2)通过学生对2'10y x ax =-+≥在(0,)+∞上恒成立问题的解法讨论，学生的可能解法有: 000⎧≤⎪≤⎨⎪∆≤⎩a x=a 解法1:对称轴x=或22 2a ∴≤ 解法2：记2()1g x x ax =-+，求其最小值大于等于0即可。

可以通过配方法或求导来求出2()1g x x ax =-+在(0,)+∞上的最小值.（3）通过对以上解法的更正（也许学生讨论会有不周到之处），追问学生是否有不对a 进行讨论的方法？可以让学生回答或教师得出本堂课要学习的方法: 常数分离法。

（4）通过对以上这几种方法的对比，得出常数分离法的优点，引起学生的学习兴趣。

（5）对该引例进行小结：①若()f x 在M 上递增/()0f x ⇒≥在M 上恒成立；②使用基本不等式需满足：“一正、二定、三相等”。

典例剖析：例1．已知函数3()31f x x ax =+-的导函数为/()f x ，/()()3g x f x ax =--. （1）若/()60x g x ⋅+>对一切2x ≥恒成立，求实数a 的取值范围；（2）若对满足01a ≤≤的一切a 的值，都有()0g x <，求实数x 的取值范围.解：（1）/22()33()333f x x a g x x a ax =+∴=+-- /()6g x x a ∴=-即2660x ax -+>对一切2x ≥恒成立学生回答：解法1：即66a x x<+对一切2x ≥恒成立 记6()6h x x x=+在2x ≥上恒成立 有/26()6h x x=-在2x ≥上恒大于0， 即6()6h x x x=+在2x ≥上单调递增 min ()(2)15h x h ∴== 15a ∴<可能的陷阱：学生会回答用基本不等式去解决，利用基本不等式解决时要注意适用的条件：“一正、二定、三相等、四检验”会发现取不到等号。