空间向量的坐标表示

空间向量的坐标表示与数量积空间向量是指具有大小和方向的量，可以用坐标表示。

在三维空间中，一个向量可以由其在坐标系中的坐标表示。

坐标表示的形式可以是直角坐标、柱坐标或球坐标等，而本文将主要讨论向量的直角坐标表示以及与数量积的关系。

一、直角坐标表示直角坐标系是三维空间中最常用的坐标系。

一个向量在直角坐标系中的坐标表示为(x, y, z)，其中x、y、z分别表示向量在X轴、Y轴和Z轴上的投影长度。

向量的坐标表示使我们能够方便地进行向量运算，比如向量的加减、数量积等。

下面以一个具体的向量为例进行说明。

假设有向量A，它的起始点在原点O(0, 0, 0)，终点在点P(x, y, z)。

根据直角坐标系的定义，我们可以得到向量A的坐标表示为A(x, y, z)。

这表示向量A在X轴上的投影长度为x，在Y轴上的投影长度为y，在Z轴上的投影长度为z。

二、数量积的计算数量积是一种向量运算，它可以衡量两个向量之间的相似程度。

数量积的计算公式为：A·B = |A||B|cosθ其中，A·B表示向量A和向量B的数量积，|A|和|B|分别表示向量A和向量B的长度，θ表示向量A与向量B之间的夹角。

具体地，我们可以通过向量的坐标来计算数量积。

设向量A的坐标表示为A(x1, y1, z1)，向量B的坐标表示为B(x2,y2, z2)。

根据数量积的计算公式，我们可以得到：A·B = x1x2 + y1y2 + z1z2三、应用举例假设有向量A(1, 2, 3)和向量B(4, 5, 6)，我们可以通过坐标表示计算它们的数量积。

首先，根据数量积的计算公式，我们可以得到：A·B = (1)(4) + (2)(5) + (3)(6)= 4 + 10 + 18= 32因此，向量A和向量B的数量积为32。

数量积的计算结果可以告诉我们这两个向量之间的相似程度。

如果数量积为正数，表示两个向量之间的夹角为锐角；如果数量积为负数，表示两个向量之间的夹角为钝角；如果数量积为零，表示两个向量垂直。

向量的坐标表示在数学中，向量是一个具有大小和方向的量。

为了方便计算和分析，我们常常使用向量的坐标表示方法。

向量的坐标表示可以帮助我们更直观地理解和操作向量。

一、二维对于二维空间中的向量，我们可以使用横纵坐标来表示。

假设有一个向量v，它在二维平面上的起点为原点(0,0)，终点为点P(x,y)，那么向量v的坐标表示就是(x,y)。

例如，有一个向量v，它在二维平面上的起点为原点，终点为点P(3,4)。

那么向量v的坐标表示为(3,4)。

二、三维对于三维空间中的向量，我们可以使用三个坐标轴来表示。

假设有一个向量u，它在三维空间中的起点为原点(0,0,0)，终点为点Q(x,y,z)，那么向量u的坐标表示就是(x,y,z)。

例如，有一个向量u，它在三维空间中的起点为原点，终点为点Q(1,2,3)。

那么向量u的坐标表示为(1,2,3)。

三、向量表示方法的应用向量的坐标表示方法在各个领域都有广泛应用。

以下是一些常见应用：1. 几何学：在几何学中，向量的坐标表示方法被用于描述线段、向量的长度和方向等概念。

通过向量的坐标表示，我们可以更方便地计算几何图形的属性。

2. 物理学：在物理学中，向量的坐标表示方法被用于描述物体的位移、速度、加速度等物理量。

通过向量的坐标表示，我们可以更精确地描述物体在空间中的运动状态。

3. 计算机图形学：在计算机图形学中，向量的坐标表示方法被广泛用于表示图像的位置、方向、形状等信息。

通过向量的坐标表示，我们可以实现计算机生成的三维图形和特效效果。

4. 统计学：在统计学中，向量的坐标表示方法被用于表示多维数据和样本。

通过向量的坐标表示，我们可以进行数据分析、模式识别等统计学方法。

总结：通过向量的坐标表示方法，我们可以更直观地理解和操作向量。

无论是二维向量还是三维向量，坐标表示都为我们提供了便利的计算和分析工具。

向量的坐标表示方法在几何学、物理学、计算机图形学和统计学等领域都有重要的应用。

掌握向量的坐标表示方法对于理解和应用相关概念都非常重要。

空间矢量的坐标表示法一、中点公式坐标空间中，P （x 1 , y 1 , z 1），Q （x 2 , y 2 , z 2）两点连线段的中点M 的坐标为121212,,222x x y y z z ⎛⎫ ⎪⎝⎭＋＋＋。

二、距离公式坐标空间中，P （x 1 , y 1 , z 1），Q （x 2 , y 2 , z 2）两点的距离为PQ三、空间矢量的坐标表示法 1. 对于坐标空间中的任意一个矢量v v ，将始点放在原点，若其终点坐标为（a , b , c ），则 v v ＝（a , b , c ），称为v v 的坐标表示。

其中a 、b 、c 分别称为矢量v v 的x 分量、y 分量、z 分量。

2. 若A 、B 两点的坐标分别为A （x 1 , y 1 , z 1），B （x 2 , y 2 , z 2），则： AB uu u v ＝（x 2－x 1 , y 2－y 1 , z 2－z 1）。

四、空间矢量的加、减法与系数乘法 设a v ＝（x 1 , y 1 , z 1），b v ＝（x 2 , y 2 , z 2）为坐标空间中的两矢量，则： 1. a v ＋b v ＝（x 1＋x 2 , y 1＋y 2 , z 1＋z 2）。

2. a v －b v ＝（x 1－x 2 , y 1－y 2 , z 1－z 2）。

3. r a v ＝（rx 1 , ry 1 , rz 1），其中r 为实数。

五、分点公式设A （x 1 , y 1 , z 1），B （x 2 , y 2 , z 2）是坐标空间中的相异两点，若P 点在线段AB 上，且PA ：PB ＝m ：n ，则P 点坐标为121212,,nx mx ny my nz mz m nm n m n ⎛⎫ ⎪⎝⎭＋＋＋＋＋＋。

六、线性组合 1. 当O ，A ，B 三点不共线时，则对同平面上的任一点P ，OP uuv 都可写成OA uu v 和OB uuv 的线性 组合，而且表示法是唯一的，即存在唯一一组实数x ，y 使得OP uuv ＝x OA uu v ＋y OB uuv 。

解析几何中空间向量的坐标表示法及应用空间向量是指在三维空间中具有大小和方向的矢量，是解析几何中重要的概念。

在几何学、物理学、工程学等领域中，空间向量的概念都具有重要的应用价值。

在这篇文章中，我们将探讨空间向量的坐标表示法及其应用，希望能对各位读者有所帮助。

一、空间向量的坐标表示法在二维平面中，一个向量可以由其在平面直角坐标系下的坐标表示。

同样地，在三维空间中，一个向量可以由其在空间直角坐标系下的坐标表示。

这里我们简单地介绍一下空间向量的坐标表示法。

在空间直角坐标系下，任意一个向量都可以表示成一个三元组$(x,y,z)$ 的形式。

其中，$x$，$y$，$z$ 分别表示向量在 $x$，$y$，$z$ 方向上的投影长度，也就是向量的坐标。

例如，我们有一向量 $\vec{V}$，其起点为点 $A(x_1,y_1,z_1)$，终点为点 $B(x_2,y_2,z_2)$。

则 $\vec{V}$ 的坐标表示为 $(x_2-x_1,y_2-y_1,z_2-z_1)$。

这里的坐标表示是相对于原点 $(0,0,0)$ 的。

不难发现，空间向量的坐标表示方式与向量的平移无关，因此在坐标系中选取不同的点作为坐标原点，其坐标表示方式是相同的。

二、空间向量的应用空间向量的研究及其应用涉及到多个学科领域，例如几何学、物理学、工程学、计算机科学等。

在下面的内容中，我们将以几何学为例，介绍一些空间向量的基本应用。

1. 向量的加法及减法空间向量的加法及减法同样可以通过坐标表示法来求解。

具体而言，设向量 $\vec{a}$ 和向量 $\vec{b}$ 的坐标分别为$(a_1,a_2,a_3)$ 和 $(b_1,b_2,b_3)$，则向量 $\vec{a}+\vec{b}$ 的坐标表示为 $(a_1+b_1,a_2+b_2,a_3+b_3)$；向量 $\vec{a}-\vec{b}$ 的坐标表示为 $(a_1-b_1,a_2-b_2,a_3-b_3)$。

2－3 空間向量的坐標表示法空間向量的坐標表示法要點整理要點整理甲、空間向量的坐標表示法1. 空間向量的表示法：設P (x 1 , y 1 , z 1) , Q (x 2 , y 2 , z 2)– y 1 , z 2 – z 1)，||。

2. 方向角：= (a , b , c )為一向量，若從x 軸、y 軸、z 的有向角分別為α、β、γ（0 ≤ α , β , γ ≤ π），則α , β , γ3. 方向餘弦：若α , β , γ= (a , b , c )的方向角，則稱cos α =222c b a a ++，cos β =222c b a b ++，cos γ的方向餘弦。

【註】 (1)任意非零向量的方向餘弦必滿足cos 2α + cos 2β + cos 2γ = 1，且sin 2α + sin β + sin γ = 2α| cos β| cos γ)。

4. 分點公式：設P (a 1 , b 1 , c 1)，Q (a 2 , b 2 , c 2)，R 為直線PQ 上一點，滿足RQ PR := m : n 。

(1)若P −R −Q (R 為PQ 的內分點)，則R 的坐標為),,(212121nm mc nc n m mb nb n m ma ma ++++++= 。

(2)若P −Q −R (R 為PQ 的外分點)，則R 的坐標為,,(212121nm mc nc n m mb nb n m ma na −+−−+−−+−。

乙、空間向量的內積1. 內積：= (a 1 , a 2 , a 3)= (b 1 , b 2 , b 3)，= || cos θ = a 1b 1 + a 2b 2 + a 3b 3。

2. 內積性質：(1)⋅ (2) ⋅+) =+⋅。

(3)⋅= || || cos0° = |2。

(4)⇔。

3. 向量的夾角： 若均非零向量，且其夾角為θ（0 ≤ θ < π），則cos θ= =232221232221332211b b b a a a b a b a b a ++⋅++++。

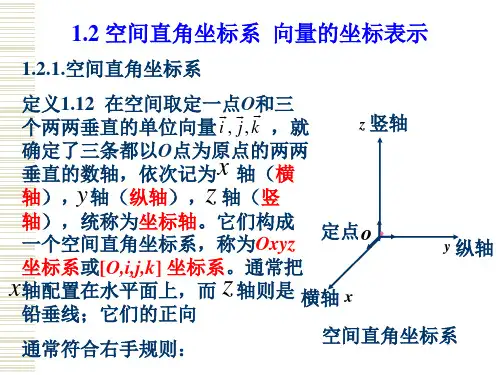
空间向量的坐标表示本次课课堂教学内容要点一、空间向量的基本定理1.空间向量的基本定理：如果三个向量a、b、c不共面，那么对空间任一向量p，存在唯一的有序实数组x、y、z，使p=x a+y b+z c．2.基底、基向量概念：由空间向量的基本定理知，若三个向量a、b、c不共面，那么所有空间向量所组成的集合就是{p|p=x a+y b+z c，x、y、z∈R}，这个集合可看做是由向量a、b、c生成的，所以我们把{a、b、c}称为空间的一个基底．a、b、c叫做基向量，空间任意三个不共面的向量都可构成空间的一个基底．要点诠释:1.空间任意三个不共面的向量都可以作为空间向量的一个基底；2.由于0可视为与任意一个非零向量共线，与任意两个非零向量共面，所以，三个向量不共面，就隐含着它们都不是0；3.一个基底是指一个向量组，一个基向量是指基底中的某一个向量，二者是相关联的不同概念．要点二、空间向量的坐标表示1.单位正交基底若空间的一个基底的三个基向量互相垂直，且长为1，这个基底叫单位正交基底，常用{,,}i j k 表示；2.空间直角坐标系在空间选定一点O 和一个单位正交基底{,,}i j k ，以点O 为原点，分别以,,i j k 的方向为正方向建立三条数轴：x 轴、y 轴、z 轴，它们都叫坐标轴．我们称建立了一个空间直角坐标系O xyz -，点O 叫原点，向量,,i j k 都叫坐标向量。

通过每两个坐标轴的平面叫坐标平面，分别称为xOy 平面，yOz 平面，zOx 平面；3.空间直角坐标系中的坐标给定一个空间直角坐标系和向量a ，其坐标向量为i ，j ，k ，若a =a 1i+a 2j+a 3k ，则有序数组（a 1，a 2，a 3）叫做向量a 在此直角坐标系中的坐标，上式可简记作a =（a 1，a 2，a 3）．在空间直角坐标系Oxyz 中，对于空间任一点A ，对应一个向量OA ，若OA xi yj zk =++ ，则有序数组（x ，y ，z ）叫点A 在此空间直角坐标系中的坐标，记为A （x ，y ，z ），其中x 叫做点A 的横坐标，y 叫点A 的纵坐标，z 叫点A 的竖坐标．写点的坐标时，三个坐标之间的顺序不可颠倒．要点诠释：1.空间任一点P 的坐标的确定．过P 作面xOy 的垂线，垂足为P ＇，在面xOy 中，过P ＇分别作x 轴、y 轴的垂线，垂足分别为A 、C ，则x=|P ＇C|，y=|AP ＇|，z=|PP ＇|．如图．2.空间相等向量的坐标是唯一的；另外，零向量记作0(0,0,0)= 。