空间向量的坐标运算

空间向量的坐标与运算空间向量是向量的一种特殊形式，用于表示空间中的位置和方向。

在三维空间中，我们可以用三个坐标轴来表示空间向量的三个分量，分别是x、y和z轴的坐标。

通过对空间向量的坐标进行运算，我们可以进行各种有趣的空间几何计算。

首先，我们来看一下空间向量的表示。

一个三维向量可以表示为(Vx, Vy, Vz)，其中Vx、Vy和Vz分别是向量在x、y和z轴上的坐标。

如果我们在空间中有两点A(x1, y1, z1)和B(x2, y2, z2)，我们可以通过这两点的坐标求出空间向量AB的坐标。

坐标运算是对空间向量的坐标进行运算。

常用的坐标运算有加法、减法、数量乘法和点乘。

首先，让我们来看一下向量的加法和减法。

如果有两个向量A(x1,y1, z1)和B(x2, y2, z2)，它们的坐标和分别是(x1+x2, y1+y2, z1+z2)。

也就是说，向量的坐标相加就是分别将对应坐标相加。

同样，向量的减法也是使用相同的方式。

接下来，我们来看一下向量的数量乘法。

向量的数量乘法是将向量的坐标分别乘以一个标量。

如果有一个向量A(x, y, z)和一个标量k，那么A乘以k的结果就是(kx, ky, kz)。

最后，我们来看一下向量的点乘。

向量的点乘也叫数量积，结果是一个标量。

如果有两个向量A(x1, y1, z1)和B(x2, y2, z2)，它们的点乘结果等于x1*x2 + y1*y2 + z1*z2。

点乘的结果可以用来判断两个向量之间的夹角、平行性等。

除了以上的基本运算外，我们还可以进行其他更复杂的运算，如叉乘、模长计算等。

叉乘是两个向量的乘积，结果是一个新的向量。

叉乘的结果正交于原来的两个向量，并且模长与原向量之积等于原向量之间的夹角的正弦值。

空间向量的坐标和运算在几何学、物理学等许多学科中都有广泛的应用。

通过对坐标的运算，我们可以计算两点之间的距离、判断两个向量之间的关系等。

在计算机图形学、计算机游戏等领域，也经常使用空间向量的坐标和运算来表示和处理三维图形。

高二数学空间向量的坐标运算【本讲主要内容】空间向量的坐标运算空间直角坐标系，空间向量的坐标表示，空间向量的坐标运算，空间向量平行，垂直的坐标表示形式。

【知识掌握】 【知识点精析】1. 空间直角坐标系（1）单位正交基底，空间直角坐标系，右手直角坐标系（2）坐标：在空间直角坐标系O-xyz 中，对空间任一点A ，对应一个向量OA →，于是存在唯一的有序实数组x 、y 、z ，使OA xi yj zk =++，则实数组（x ，y ，z ）叫做点A 在此空间直角坐标系中的坐标。

2. 向量的直角坐标运算设a a a ab b b b ==()()123123，，，，，则a b a b a b a b +=+++()112233，，a b a b a b a b -=---()112233，，a b a b a b a b ⋅=++112233a b a b a b a b R //⇔===∈112233λλλλ，，，或a b a b a b 112233==a b a b a b a b ⊥⇔++=11223303. 夹角和距离公式（1）夹角公式：设a a a ab b b b ==()()123123，，，，，则cos <>=++++⋅++a b a b a b a b a a a b b b ，112233122232122232（2）距离公式：设A x y z B x y z ()()111222，，，，， 则d x x y y z z AB =-+-+-()()()122122122（3）平面的法向量：如果表示向量a 的有向线段所在直线垂直于平面α，则称这个向量垂直于平面α，记作a ⊥α。

如果 a ⊥α，那么向量a 叫做平面α的法向量。

【解题方法指导】1. 在证明线线平行时，利用a b a b //⇔=λ即()()a a a b b b 123123，，，，=λλλ，在证明线面平行或面面平行时，需转化为线线平行问题。

空间向量坐标运算空间向量是指在空间中有大小和方向的线段。

空间向量的坐标运算包括向量的加法、减法、数乘和内积。

下面将对这些运算进行详细介绍。

一、向量的加法设空间中有两个向量A和B，它们的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)。

向量的加法即将两个向量的对应分量相加得到一个新的向量C。

它的坐标为(Ax+Bx, Ay+By, Az+Bz)。

例如，设A = (1, 2, 3)和B = (4, 5, 6)，则A+B = (1+4, 2+5, 3+6) = (5, 7, 9)。

二、向量的减法向量的减法是指将一个向量减去另一个向量。

设向量A和B的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)，则向量A减去向量B的坐标为(Ax-Bx, Ay-By, Az-Bz)。

例如，设A = (1, 2, 3)和B = (4, 5, 6)，则A-B = (1-4, 2-5, 3-6) = (-3, -3, -3)。

三、向量的数乘向量的数乘是指一个向量乘以一个实数。

设向量A的坐标为(Ax, Ay, Az)，实数k，则向量A乘以实数k的坐标为(kAx, kAy, kAz)。

例如，设A = (1, 2, 3)，k = 2，则kA = (2*1, 2*2, 2*3) = (2, 4,6)。

四、向量的内积向量的内积又称为点乘，它是两个向量之间的一种运算。

设向量A和B的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)，则向量A与向量B的内积为Ax*Bx + Ay*By + Az*Bz。

例如，设A = (1, 2, 3)和B = (4, 5, 6)，则A·B = 1*4 + 2*5 +3*6 = 32。

向量的内积有以下几个性质：1. 交换律：A·B = B·A；2. 分配律：(A+B)·C = A·C + B·C；3. 数乘结合律：(kA)·B = k(A·B) = A·(kB)。

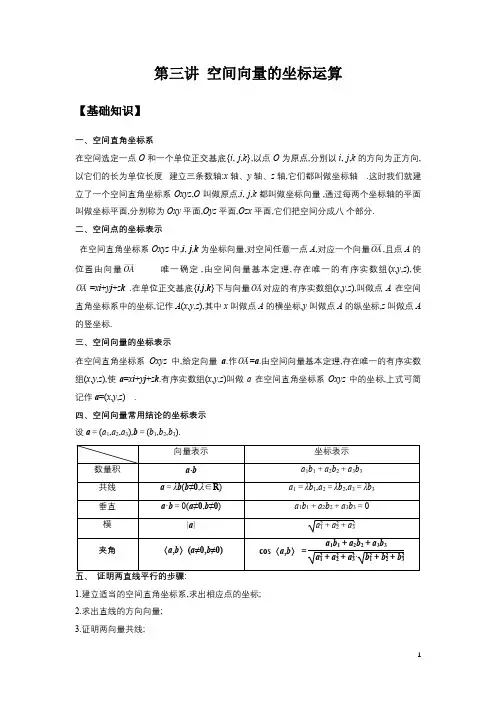
第三讲空间向量的坐标运算【基础知识】一、空间直角坐标系在空间选定一点O和一个单位正交基底{i, j,k},以点O为原点,分别以i, j,k的方向为正方向,以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i, j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.二、空间点的坐标表示在空间直角坐标系Oxyz中,i, j,k为坐标向量,对空间任意一点A,对应一个向量OA,且点A的位置由向量OA唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使OA=x i+y j+z k.在单位正交基底{i,j,k}下与向量OA对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A 的竖坐标.三、空间向量的坐标表示在空间直角坐标系Oxyz中,给定向量a.作OA=a.由空间向量基本定理,存在唯一的有序实数组(x,y,z),使a=x i+y j+z k.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,上式可简记作a=(x,y,z).四、空间向量常用结论的坐标表示设a＝(a1,a2,a3),b＝(b1,b2,b3).1.建立适当的空间直角坐标系,求出相应点的坐标;2.求出直线的方向向量;3.证明两向量共线;4.说明其中一个向量所在直线上的一点不在另一个向量所在的直线上,即表示方向向量的 有向线段不共线,即可得证. 六、证明两直线垂直的步骤:1.根据已知条件和图形特征,建立适当的空间直角坐标系,正确地写出各点的坐标;2.根据所求点的坐标求出两直线方向向量的坐标;3.计算两直线方向向量的数量积为0;4.由方向向量垂直得到两直线垂直. 七、求两异面直线夹角的步骤1.求异面直线a ,b 上的方向向量的坐标:a =(x 1,y 1,z 1),b =(x 2,y 2,z 2);2.利用公式cos<a ,b >= 求解;3.设异面直线a ,b 所成的角为θ,则cos θ=|cos<a ,b >|.【考点讲解】考点一：求点的坐标例1．已知空间点(3,1,4)P --，则点P 关于y 轴对称的点的坐标为（ ） A ．(3,1,4)--- B ．(3,1,4)-- C ．(3,1,4)-D ．(3,1,4)考点二：求向量的坐标例2．给定空间三个点()1,1,2A ､()3,7,1B -､()5,4,0C . (1)求以向量AB ､AC 为一组邻边的平行四边形的面积S ； (2)求与向量AB ､AC 都垂直的单位向量a .考点三：线性运算的坐标表示例3．已知向量()3,2,5a =-，()1,5,1b =-，则3a b -=（ ） A ．8,11(),14-B ．9,3(),15-C ．10,1(),16-D ．(0,13,2)考点四：数量积运算的坐标表示例4．（多选）已知空间向量()1,1,1a =，()1,0,2b =-，则下列正确的是（ ） A ．()0,1,3a b +=B ．3a =C ．2a b ⋅=D ．a <，4b π→>=考点五：求长度或距离例5．空间两点()1,2,3A 、()2,0,5B 之间的距离为______．考点六：求角度例6．已知()cos ,1,sin a αα=-，()sin ,1,cos b αα=-，则向量a b +与a b -的夹角为（ ） A ．90° B ．60°C ．30°D ．0°考点七：根据平行或垂直求参数的值例7.已知点(2,0,2)A -，(1,1,2)B -，(3,0,4)C -，设a AB =，b AC =． (1)求a ，b 夹角的余弦值．(2)若向量ka b +，2ka b -垂直，求k 的值． (3)若向量a b λ-，a b λ-平行，求λ的值．【课堂练习】1.已知向量(2,1,3),(,2,6)a b x →→=-=-，若a b →→⊥，则实数x 的值为（ ） A ．7B ．8C ．9D ．102.若向量()1,,0a λ=，(2,1,2)b =-且a 与b 的夹角余弦值为23，则实数λ等于（ ） A ．0B ．－43C ．0或－43D ．0或433.平行六面体1111ABCD A B C D -中，()()11,2,3,1,2,4AC C =-，则点1A 的坐标为（ ） A ．()0,4,7B ．()2,0,1-C ．()2,0,1-D ．()2,0,14. （多选）已知平面{}00P n P P α=⋅=，其中点0P 是平面α内的一定点，n 是平面α的一个法向量，若0P 坐标为()2,3,4，()1,1,1n =，则下列各点中在平面α内的是（ ） A ．()1,3,5B ．()4,3,2C ．()2,3,8-D ．()2,3,8-5. （多选）已知正方体1111ABCD A B C D -的棱长为1，,,P Q R 分别在111,,AB CC D A 上，并满足111(01)1D R AP CQ a a PB QC RA a===<<-，设1,,AB i AD j AA k ===，设PQR ∆的重心为G ，下列说法正确的是（ ）A ．向量,,i j i j k +-可以构成一组基底B ．当12a =时，111j+333DG i k =-C ．当13a =时，PQ 在平面1ADD ．对任意实数a ，总有0RG DG ⋅=6.已知空间三点A (1，-1，-1)，B (-1，-2，2)，C (2，1，1)，则AB 在AC 上的投影向量的模是______.7.设空间向量,,i j k 是一组单位正交基底，若空间向量a 满足对任意的,,x y a xi y j --的最小值是2，则3a k +的最小值是_________．8.已知空间中三点(),1,2A m -，()3,1,4B -，()1,,1C n -． (1)若A ，B ，C 三点共线，求m n +的值；(2)若AB ，BC 的夹角是钝角，求m n +的取值范围．【课后练习】1.若点(2,5,1)A --，(1,4,2)B ---，(3,3,)C m n +-在同一条直线上，则m n -=（ ） A ．21B ．4C ．-4D ．102.已知直线2,l l l 的方向向量分别为()()1,4,2,2,1,a b m =-=-，若12l l ⊥，则m 等于（ ） A ．0B ．1C ．2D ．33.设,x y ∈R ，向量(,1,1),(1,,1),(2,4,2)a x b y c ===-，且,a c b c ⊥∥，则||x y +=（ ） A ．1B ．2C ．3D ．44.已知(1,0,1)a =，(,1,2)b x =，且3a b ⋅=，则向量a 与b 的夹角为（ ） A ．60︒B ．120︒C ．30D ．150︒5. （多选）对于非零空间向量a ，b ，c ，现给出下列命题，其中为真命题的是（ ） A ．若0a b ⋅<，则a ，b 的夹角是钝角 B ．若()1,2,3a =，()1,1,1b =--，则a b ⊥ C ．若a b b c ⋅=⋅，则a c =D ．若()1,0,0a =，()0,2,0b =，()0,0,3c =，则a ，b ，c 可以作为空间中的一组基底 6．（多选）已知空间向量()2,1,1a =--，()3,4,5b =，则下列结论正确的是（ ） A ．()2//a b a + B ．53a b = C ．()56a a b ⊥+D ．a 与b 夹角的余弦值为7．（多选）已知空间中三点()0,1,0A ，()1,2,0B ，()1,3,1C -，则正确的有（ ） A ．AB 与AC 是共线向量 B ．AB 的单位向量是()1,1,0C ．AB 与BC 夹角的余弦值是D ．平面ABC 的一个法向量是()1,1,3-8. 平面α经过点()0,0,2A 且一个法向量()1,1,1n =--，则平面α与x 轴的交点坐标是______．9．已知()1,1,2A -，()1,0,1B -．设D 在直线AB 上，且2AD DB =，设1,,13C λλλ⎛⎫++ ⎪⎝⎭，若CD AB ⊥，则实数λ=______．10.空间中，两两互相垂直且有公共原点的三条数轴构成直角坐标系，如果坐标系中有两条坐标轴不垂直，那么这样的坐标系称为“斜坐标系”.现有一种空间斜坐标系，它任意两条数轴的夹角均为60°，我们将这种坐标系称为“斜60°坐标系”.我们类比空间直角坐标系，定义“空间斜60°坐标系”下向量的斜60°坐标：,,i j k 分别为“斜60°坐标系”下三条数轴（x 轴､y 轴､z 轴）正方向的单位向量，若向量n xi yj zk =++，则n 与有序实数组（x ，y ，z ）相对应，称向量n 的斜60°坐标为[x ，y ，z ]，记作[,,]n x y z =. (1)若[]1,2,3a =，[1,1,2]b =-，求a b +的斜60°坐标；(2)在平行六面体11ABCD ABC D -中，AB =AD =2，AA 1=3，1160BAD BAA DAA ∠=∠=∠=，如图，以{}1,,AB AD AA 为基底建立“空间斜60°坐标系”.①若1BE EB =，求向量1ED 的斜60坐标； ①若[]2,,0AM t =，且1AM AC ⊥，求AM .。

空间向量坐标运算空间向量是指具有大小和方向的直线段，在三维空间中通常用坐标表示。

空间向量的坐标运算包括向量的加法、减法、数量乘法、点乘和叉乘等。

下面将详细介绍这些运算。

1. 向量的加法和减法向量的加法和减法是指将两个向量相加或相减得到一个新的向量，其坐标运算规律如下：- 加法：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的和的坐标为(u1+v1, u2+v2, u3+v3)；- 减法：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的差的坐标为(u1-v1, u2-v2, u3-v3)。

2. 向量的数量乘法向量的数量乘法是指将一个向量乘以一个实数得到一个新的向量，其坐标运算规律如下：- 数量乘法：若向量u的坐标为(u1, u2, u3)，实数k，则向量u 乘以k的坐标为(k*u1, k*u2, k*u3)。

3. 向量的点乘向量的点乘又称为内积，是指将两个向量进行乘法运算得到一个标量（实数），其计算公式如下：- 点乘：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的点乘的结果为u1*v1 + u2*v2 + u3*v3。

4. 向量的叉乘向量的叉乘又称为外积，是指将两个向量进行乘法运算得到一个新的向量，其计算公式如下：- 叉乘：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的叉乘的坐标为((u2*v3 - u3*v2), (u3*v1 -u1*v3), (u1*v2 - u2*v1))。

通过以上的描述可以看出，向量的加法、减法、数量乘法都是按照对应位置进行运算，只要对应坐标进行相加、相减或乘以相同的实数即可。

点乘和叉乘则需要对应坐标进行特定的运算。

需要注意的是，向量的坐标运算不关心向量的起点和终点，只关心向量的大小和方向。

9.6空间向量的坐标运算亠、空间直角坐标系:如果空间的一个基底的三个基向量互相垂直，且长都为1，这个基底叫做单位正交基底，常用｛i, j,k｝表示。

r r u 在空间选定一点0和一个单位正交基底｛i, j,k｝，r r u J 以点O为原点，分别以i、j、k的方向为正方向建立三条数轴：x轴、y轴、z轴，它们都叫做坐标轴。

这时我们称建立了一个空间直角坐标系O- xyz，点0叫r r u做原点，向量i、j、k都叫做坐标向量。

通过每两个坐标轴的平面叫做坐标平面，分别称为xOy平面，yOz 平面，zOx平面。

u注意：①作空间直角坐标系O- xyz时，一般使? xOy 135 °（或45 °）, ? yOz 90 °。

②在空间直角坐标系中，让右手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指指向z轴的正方向，则称这个坐标系为右手直角坐标系。

说明右手直角坐标系的特点是：从Ox到Oy是逆时针方向。

③如无特别说明，以后建立的坐标系都是右手直角坐标系。

给定一个空间直角坐标系和向量a，且设i、j、k 为坐标向量，根据空间向量基本定理可知：存在唯一的有序实数组(a i,a2, a3)，使r r r ua = a i i + a2 j + a3 k有序实数组(a i,a2,a3)叫做向量\在空间直角坐标系O- xyz中的坐标，可简记作ra = (a i, a2, a3)z在空间直角坐标系O- xyz中，对空间任一点A，r对应一个向量OA，于是存在唯一的有序实数组x、y、z，使um r r uOA = xi + yj + zk有序实数组(x, y, z)叫做点A的坐标，记作A (x,y,z )，其中x 叫做点A 的横坐标，y 叫做点A 的 纵坐标,z 叫做点A 的竖坐标。

二、空间向量的直角坐标运算：r rI •设 a = (a i , a 2, a 3)? b = (bi ,6 ,b s )，则 ① a + b = (a i + b,a 2 + 6,a 3+ b 3); r r② a - b = (a i - b i ,a 2- b 2,a 3- b s );r③ I a = (l a i ,l a 2,l a 3)(l ? R );r r④ a ?b a i b i + a 2 b 2 + a 3 b s ;r r⑤ a 八 b ? a i b i a 26+ a 3b s = 0;l a i = l bi ^a 2 l b 2(l ? R ) =l b 3①AB 的中点坐标是 严产，皿产，电产); uuur uuur uuur② AB = OB - OA =(X 2- x i , y 2- y i 卫-Z i )。

9.6 空间向量的坐标运算一、空间直角坐标系：如果空间的一个基底的三个基向量互相垂直，且长都为1，这个基底叫做单位正交基底，常用{},,i j k r r u r表示。

在空间选定一点O 和一个单位正交基底{},,i j k r r u r，以点O 为原点，分别以i r 、j r 、k u r的方向为正方向建立三条数轴：x 轴、y 轴、z 轴，它们都叫做坐标轴。

这时我们称建立了一个空间直角坐标系-O xyz ，点O 叫做原点，向量i r 、j r 、k u r都叫做坐标向量。

通过每两个坐标轴的平面叫做坐标平面，分别称为xOy 平面，yOz 平面，zOx 平面。

注意：O xyz时，一般使①作空间直角坐标系-?xOy135o（或45o），?yOz90o。

②在空间直角坐标系中，让右手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指指向z轴的正方向，则称这个坐标系为右手直角坐标系。

说明右手直角坐标系的特点是：从Ox到Oy是逆时针方向。

③如无特别说明，以后建立的坐标系都是右手直角坐标系。

给定一个空间直角坐标系和向量a r，且设i r 、j r 、k u r为坐标向量，根据空间向量基本定理可知：存在唯一的有序实数组(),,a a a 123，使=++a a i a j a k 123r r r u r有序实数组(),,a a a 123叫做向量a r在空间直角坐标系-O xyz 中的坐标，可简记作()=,,a a a a 123r在空间直角坐标系-O xyz 中，对空间任一点A ，对应一个向量OA uu u r，于是存在唯一的有序实数组x 、y 、z ，使=++OA xi y j zk u u u r r r u r有序实数组(),,x y z 叫做点A 的坐标，记作(),,A x y z ，其中x 叫做点A 的横坐标，y 叫做点A 的纵坐标，z 叫做点A 的竖坐标。

二、空间向量的直角坐标运算：Ⅰ．设()=,,a a a a 123r ，()=,,b b b b 123r，则 ①()+=+++,,a b a b a b a b 112233r r； ②()-=---,,a b a b a b a b 112233r r；③()()=?,,a a a a R l l l l l 123r； ④?++a b a b a b a b 112233r r； ⑤^?+=a b a b a b a b 1122330r r；⑥()ì=ïïï??íïïï=ïî//a b a b a b R a b l l l l 112233r r 。

空间向量运算的坐标表示1.理解空间向量坐标的概念，会确定一些简单几何体的顶点坐标．2.掌握空间向量的坐标运算规律，会判断两个向量的共线或垂直．3.掌握空间向量的模、夹角公式和两点间距离公式，并能运用这些知识解决一些相关问题．1．空间向量的坐标运算设a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3)，则a ＋b ＝(a 1＋b 1，a 2＋b 2，a 3＋b 3)，a －b ＝(a 1－b 1，a 2－b 2，a 3－b 3)，λa ＝(λa 1，λa 2，λa 3)，a ·b ＝a 1b 1＋a 2b 2＋a 3b 3．2．空间向量的平行、垂直及模、夹角设a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3)，则a ∥b ⇔a ＝λb ⇔a 1＝λb 1，a 2＝λb 2，a 3＝λb 3(λ∈R )；a ⊥b ⇔a ·b|a |＝a ·a cos 〈a ，b 〉＝a ·b |a ||b |＝1122a 3b 3a 21＋a 22＋a 23b 21＋b 22＋b 23. 3．空间中两点间的距离公式在空间直角坐标系中，设A (a 1，b 1，c 1)，B (a 2，b 2，c 2)，则A ，B 两点间的距离d ＝|AB →|1．判断(正确的打“√”，错误的打“×”)(1)空间向量a ＝(1，1，1)的长度为1.( )(2)若向量a·b ＝0，则向量a 与向量b 垂直．( )(3)设a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3)，则a ∥b ⇔a 1b 1＝a 2b 2＝a 3b 3.( ) (4)任给向量a ，b ，都有a·b ≤|a ||b |.( )答案：(1)× (2)× (3)× (4)√2．已知向量a ＝(4，－2，－4)，b ＝(6，－3，2)，则下列结论正确的是( )A ．a ＋b ＝(10，－5，－6)B ．a －b ＝(2，－1，－6)C ．a ·b ＝10D ．|a |＝6答案：D3．已知A (3，3，3)，B (6，6，6)，O 为原点，则OA→与BO →的夹角是( )A ．0B ．πC.3π2 D ．2π答案：B4．已知a ＝(2，1，3)，b ＝(－4，5，x )，若a ⊥b ，则x ＝________． 答案：1探究点一 空间向量的坐标运算已知O 为原点，A ，B ，C ，D 四点的坐标分别为A (2，－4，1)，B (3，2，0)，C (－2，1，4)，D (6，3，2)．求满足下列条件的点P 的坐标．(1)OP→＝2(AB →－AC →)；(2)AP →＝AB →－DC →. [解] (1)AB→－AC →＝CB → ＝(3，2，0)－(－2，1，4)＝(5，1，－4)，所以OP→＝2(5，1，－4)＝(10，2，－8)， 所以点P 的坐标为(10，2，－8)．(2)设P (x ，y ，z )，则AP→＝(x －2，y ＋4，z －1)． 又AB→＝(1，6，－1)，DC →＝(－8，－2，2)， 所以AB→－DC →＝(9，8，－3)， 所以(x －2，y ＋4，z －1)＝(9，8，－3)，所以⎩⎪⎨⎪⎧x －2＝9，y ＋4＝8，z －1＝－3，解得⎩⎪⎨⎪⎧x ＝11，y ＝4，z ＝－2，所以点P 的坐标为(11，4，－2)．向量的坐标即终点坐标减去起点坐标所得的坐标．求点的坐标时，一定要注意向量的起点是否在原点，在原点时，向量的坐标与终点坐标相同；不在原点时，向量的坐标加上起点坐标才是终点坐标．1.(1)设向量a ＝(2，1，6)，b ＝(－8，－3，2)，则①3a －4b ＝________；②12a ·b ＝________．(2)已知△ABC 中，A (2，－5，3)，AB→＝(4，1，2)，BC →＝(3，－2，5)，求顶点B 、C 的坐标及CA →.解：(1)①3a －4b ＝3(2，1，6)－4(－8，－3，2)＝(6，3，18)－(－32，－12，8)＝(38，15，10)．故填(38，15，10)．②12a ·b ＝12[2×(－8)＋1×(－3)＋6×2]＝12×(－7)＝－72.故填－72.(2)设B (x ，y ，z )，C (x 1，y 1，z 1)，所以AB →＝(x －2，y ＋5，z －3)，BC →＝(x 1－x ，y 1－y ，z 1－z )．因为AB →＝(4，1，2)，所以⎩⎪⎨⎪⎧x －2＝4，y ＋5＝1，z －3＝2解得⎩⎪⎨⎪⎧x ＝6，y ＝－4，z ＝5.所以B 的坐标为(6，－4，5)．因为BC →＝(3，－2，5)，所以⎩⎪⎨⎪⎧x1－6＝3，y 1＋4＝－2，z 1－5＝5解得⎩⎪⎨⎪⎧x 1＝9，y 1＝－6，z 1＝10.所以C 的坐标为(9，－6，10)，CA →＝(－7，1，－7).探究点二 坐标形式下的平行与垂直已知空间三点A (－2，0，2)、B (－1，1，2)、C (－3，0，4)．设a ＝AB →，b ＝AC →.(1)设|c |＝3，c ∥BC →，求c ；(2)若k a ＋b 与k a －2b 互相垂直，求k .[解] (1)因为BC →＝(－2，－1，2)且c ∥BC →，所以设c ＝λBC →＝(－2λ，－λ，2λ)(λ∈R )，所以|c |＝ （－2λ）2＋（－λ）2＋（2λ）2＝3|λ|＝3. 解得λ＝±1.所以c ＝(－2，－1，2)或c ＝(2，1，－2)．(2)因为a ＝AB→＝(1，1，0)，b ＝AC →＝(－1，0，2)， 所以k a ＋b ＝(k －1，k ，2)，k a －2b ＝(k ＋2，k ，－4)．因为(k a ＋b )⊥(k a －2b )，所以(k a ＋b )·(k a －2b )＝0，即(k －1，k ，2)·(k ＋2，k ，－4)＝2k 2＋k －10＝0.解得k ＝2或k ＝－52.将本例(2)中“若k a ＋b 与k a －2b 互相垂直”改为“若k a ＋b 与a ＋k b 互相平行”，其他条件不变，求k 的值．解：a ＝(－1＋2，1－0，2－2)＝(1，1，0)，b ＝(－3＋2，0－0，4－2)＝(－1，0，2)，所以k a ＋b ＝(k ，k ，0)＋(－1，0，2)＝(k －1，k ，2)． a ＋k b ＝(1，1，0)＋(－k ，0，2k )＝(1－k ，1，2k )，因为k a ＋b 与a ＋k b 平行，所以k a ＋b ＝λ(a ＋k b )，即(k －1，k ，2)＝λ(1－k ，1，2k )，所以⎩⎪⎨⎪⎧k －1＝λ（1－k ），k ＝λ·1，2＝λ·2k ，则⎩⎪⎨⎪⎧k ＝－1，λ＝－1或⎩⎪⎨⎪⎧k ＝1，λ＝1.(1)平行与垂直的判断①应用向量的方法判定两直线平行，只需判断两直线的方向向量是否共线；②判断两直线是否垂直，关键是判断两直线的方向向量是否垂直，即判断两向量的数量积是否为0.(2)平行与垂直的应用①适当引入参数(比如向量a ，b 平行，可设a ＝λb )，建立关于参数的方程；②选择坐标形式，以达到简化运算的目的．2.设a ＝(1，5，－1)，b ＝(－2，3，5)．(1)若(k a ＋b )∥(a －3b )，求k ；(2)若(k a ＋b )⊥(a －3b )，求k .解：k a ＋b ＝(k －2，5k ＋3，－k ＋5)．a －3b ＝(1＋3×2，5－3×3，－1－3×5)＝(7，－4，－16)．(1)因为(k a ＋b )∥(a －3b )，所以k －27＝5k ＋3－4＝－k ＋5－16，解得k ＝－13. (2)因为(k a ＋b )⊥(a －3b )，所以(k －2)×7＋(5k ＋3)×(－4)＋(－k ＋5)×(－16)＝0，解得k ＝1063.探究点三 向量夹角与长度的计算如图所示，正四棱锥S -ABCD 的侧棱长为2，底面边长为3，E 是SA 的中点，O 为底面ABCD 的中心．(1)求CE 的长；(2)求异面直线BE 与SC 所成角的余弦值．[解] 如图，以O 为原点，以OA→，OB →，OS →所在的直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系．因为侧棱长为2，底面边长为3，E 为SA 的中点，所以A ⎝ ⎛⎭⎪⎫62，0，0，S ⎝⎛⎭⎪⎫0，0，22， C ⎝ ⎛⎭⎪⎫－62，0，0，B ⎝ ⎛⎭⎪⎫0，62，0，E ⎝ ⎛⎭⎪⎫64，0，24. (1)CE →＝⎝ ⎛⎭⎪⎫364，0，24， 所以|CE →|＝⎝ ⎛⎭⎪⎫3642＋02＋⎝ ⎛⎭⎪⎫242 ＝142，即CE ＝142.⎝⎭SC →＝⎝⎛⎭⎪⎫－62，0，－22， 所以cos 〈BE →，SC →〉＝BE →·SC →|BE →|·|SC →|＝－12×2＝－12， 故异面直线BE 与SC 所成角的余弦值为12.运用空间向量的坐标运算解决立体几何问题的一般步骤(1)建系：根据题目中的几何图形建立恰当的空间直角坐标系； (2)求坐标：①求出相关点的坐标；②写出向量的坐标；(3)论证、计算：结合公式进行论证、计算；(4)转化：转化为几何结论．3.(1)已知a ＋b ＝(2，2，23)，a －b ＝(0，2，0)，则cos 〈a ，b 〉＝( )A.13B.16C.63D.66(2)已知△ABC 的顶点分别为A (1，－1，2)，B (5，－6，2)，C (1，3，－1)，则边AC 上的高BD ＝( )A ．5 B.41C ．4D ．2 5解析：(1)选C.由已知得a ＝(1，2，3)，b ＝(1，0，3)，所以cos 〈a ，b 〉＝a ·b |a ||b |＝1＋0＋36×4＝63. (2)选A.设AD→＝λAC →(λ∈R )，因为AC →＝(0，4，－3)，所以AD →＝(0，4λ，－3λ)．又AB→＝(4，－5，0)， 所以BD→＝AD →－AB →＝(－4，4λ＋5，－3λ)． 由AC →·BD →＝0，得λ＝－45，所以BD →＝⎝⎛⎭⎪⎫－4，95，125，所以|BD→|＝5，即BD ＝5.1．判断空间两向量(直线)平行与垂直的思路(1)空间两个向量平行、垂直与平面两个向量平行、垂直的表达式不一样，但实质是一致的．(2)判定空间两直线平行或垂直只需判断两直线对应的方向向量是否平行或垂直．2．特殊向量的坐标表示(1)当向量a 平行于x 轴时，纵坐标、竖坐标都为0，即a ＝(x ，0，0)(x ∈R )；(2)当向量a 平行于y 轴时，横坐标、竖坐标都为0，即a ＝(0，y ，0)(y ∈R )；(3)当向量a 平行于z 轴时，横坐标、纵坐标都为0，即a ＝(0，0，z )(z ∈R )；(4)当向量a 平行于xOy 平面时，竖坐标为0，即a ＝(x ，y ，0)(x ，y ∈R )；(5)当向量a 平行于yOz 平面时，横坐标为0，即a ＝(0，y ，z )(y ，z ∈R )；(6)当向量a 平行于xOz 平面时，纵坐标为0，即a ＝(x ，0，z )(x ，z ∈R )．1．已知a ＝(1，1，0)，b ＝(0，1，1)，c ＝(1，0，1)，p ＝a －b ，q ＝a ＋2b －c ，则p ·q ＝( )A ．－1B ．1C ．0D ．－2解析：选A.因为p ＝a －b ＝(1，0，－1)，q ＝a ＋2b －c ＝(0，3，1)，所以p ·q ＝1×0＋0×3＋(－1)×1＝－1，故选A.2．已知a ＝(1，0，1)，b ＝(x ，1，2)，且a ·b ＝3，则向量a 与b 的夹角为( )A.5π6B.2π3C.π3D.π6解析：选D.因为a ·b ＝x ＋2＝3，所以x ＝1.所以b ＝(1，1，2)．所以cos 〈a ，b 〉＝a ·b |a |·|b |所以a 与b 的夹角为π6.3．已知点A (－1，3，1)，B (－1，3，4)，若AP→＝2PB →，则点P 的坐标是________．解析：设点P (x ，y ，z )，则由AP→＝2PB →，得(x ＋1，y －3，z －1)＝2(－1－x ，3－y ，4－z )，则⎩⎪⎨⎪⎧x ＋1＝－2－2x ，y －3＝6－2y ，z －1＝8－2z ，解得⎩⎪⎨⎪⎧x ＝－1，y ＝3，z ＝3，即P (－1，3，3)． 答案：(－1，3，3)4．已知向量a ＝(x ，4，1)，b ＝(－2，y ，－1)，c ＝(3，－2，z )，且a ∥b ，b ⊥c .(1)求向量a ，b ，c ；(2)求向量a ＋c 与向量b ＋c 所成角的余弦值．解：(1)因为a ∥b ，所以x －2＝4y ＝1－1， 解得x ＝2，y ＝－4，此时a ＝(2，4，1)，b ＝(－2，－4，－1)．又由b ⊥c 得b·c ＝0，故(－2，－4，－1)·(3，－2，z )＝－6＋8－z ＝0，得z ＝2，此时c ＝(3，－2，2)．(2)由(1)得，a ＋c ＝(5，2，3)，b ＋c ＝(1，－6，1)，因此向量a ＋c 与向量b ＋c 所成角θ的余弦值为cos θ＝5－12＋338×38＝－219.[A 基础达标]1．已知向量a ＝(1，1，0)，b ＝(－1，0，2)，则|3a ＋b |为( ) A.15 B ．4C ．5 D.17解析：选D.3a ＋b ＝3(1，1，0)＋(－1，0，2)＝(3，3，0)＋(－1，0，2)＝(2，3，2)，故|3a ＋b |＝4＋9＋4＝17.2．若向量a ＝(1，1，x )，b ＝(1，2，1)，c ＝(1，1，1)，满足条件(c －a )·(2b )＝－2，则x 的值为( )A ．2B ．－2C ．0D ．1解析：选A.因为c －a ＝(0，0，1－x )，2b ＝(2，4，2)， 所以(c －a )·(2b )＝2(1－x )＝2－2x ＝－2.所以x ＝2.3．若△ABC 中，∠C ＝90°，A (1，2，－3k )，B (－2，1，0)，C (4，0，－2k )，则k 的值为( ) A.10 B ．－10C ．2 5D ．±10解析：选D.CB→＝(－6，1，2k )， CA→＝(－3，2，－k )， 则CB→·CA →＝(－6)×(－3)＋2＋2k ×(－k ) ＝－2k 2＋20＝0，所以k ＝±10.4．已知a ＝(x ，1，2)，b ＝(1，2，－y )，且(2a ＋b )∥(－a ＋2b )，则( )A ．x ＝13，y ＝1B ．x ＝12，y ＝－4C ．x ＝2，y ＝－14D ．x ＝1，y ＝－1解析：选B.2a ＋b ＝(2x ＋1，4，4－y )，－a ＋2b ＝(2－x ，3，－2y －2)，因为(2a ＋b )∥(－a ＋2b )，则存在非零实数λ，使得2a ＋b ＝λ(－a ＋2b )，所以⎩⎪⎨⎪⎧2x ＋1＝（2－x ）λ，4＝3λ，4－y ＝（－2y －2）λ，所以⎩⎨⎧x ＝12，y ＝－4. 5．若A (x ，5－x ，2x －1)，B (1，x ＋2，2－x )，则当|AB→|取最小值时，x 的值等于( )A ．19B ．－87C.87D.1914解析：选C.因为AB→＝(1－x ，2x －3，3－3x )， 所以|AB→|＝ （1－x ）2＋（2x －3）2＋（3－3x ）2 ＝ 14⎝ ⎛⎭⎪⎫x －872＋57. 故当x ＝87时，|AB→|有最小值． 6．已知a ＝(1，m ，3)，b ＝(－2，4，n )，若a ∥b ，则m －n ＝________． 解析：因为a ∥b ，所以b ＝λa .所以⎩⎪⎨⎪⎧λ＝－2，m λ＝4，3λ＝n .所以⎩⎪⎨⎪⎧λ＝－2，m ＝－2，n ＝－6.所以m －n ＝4.答案：47．已知2a ＋b ＝(0，－5，10)，c ＝(1，－2，－2)，a ·c ＝4，|b |＝12，则〈b ，c 〉＝________．解析：由题意，得|c |＝3，(2a ＋b )·c ＝0×1＋(－5)×(－2)＋10×(－2)＝－10，所以2a ·c ＋b ·c ＝－10.又a ·c ＝4，所以b ·c ＝－18，所以cos〈b ，c 〉＝b ·c |b |·|c |＝－12，所以〈b ，c 〉＝120°. 答案：120°8．若a ＝(x ，2，2)，b ＝(2，－3，5)的夹角为钝角，则实数x 的取值范围是________．解析：a·b ＝2x －2×3＋2×5＝2x ＋4，设a ，b 的夹角为θ，因为θ为钝角，所以cos θ＝a·b |a ||b |＜0，又|a |＞0，|b |＞0，所以a·b ＜0，即2x ＋4＜0，所以x ＜－2.又a ，b 不会反向，所以实数x 的取值范围是(－∞，－2)． 答案：(－∞，－2)9．已知向量a ＝(6，－3，2)，b ＝(4，－2，－4)．求：(1)|a |；(2)(3a ＋2b )·(－2a ＋b )．解：(1)|a |＝a 2＝62＋（－3）2＋22＝7.(2)因为|b |＝b 2＝42＋（－2）2＋（－4）2＝6，a ·b ＝6×4＋(－3)×(－2)＋2×(－4)＝22，所以(3a ＋2b )·(－2a ＋b )＝－6a 2＋3a ·b －4a ·b ＋2b 2＝－244.10．已知四边形ABCD 的顶点坐标分别是A (3，－1，2)，B (1，2，－1)，C (－1，1，－3)，D (3，－5，3)，求证：四边形ABCD 是一个。