当前位置：文档之家 › 沈阳建筑大学城市建设学院-理论力学练习册答案-第十五章 虚位移原理

沈阳建筑大学城市建设学院-理论力学练习册答案-第十五章 虚位移原理

  • 格式：doc
  • 大小：365.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

虚位移与虚位移原理

虚位移与虚位移原理

虚位移与虚位移原理虚位移与虚位移原理2010-04-22 10：528.2.1虚位移为了便于理解虚位移的概念，现把虚位移和实位移进行对比阐述。

1实位移--位置函数的微分实位移是质点系在微小的时间间隔内实际发生的位移，可用位置函数的微分表示。

设由n个质点组成的完整约束系统，其自由度为k，选取一组广义坐标，则每个点的位置可用其位置矢径表示。

满足该质点系的约束方程，取其微分(8-4)式(8-4)中，是满足约束条件的增量，是系统受不平衡力系作用而实际发生的微小位移，由动力学方程和运动初始条件确定。

由上式得到的不但是约束许可的，而且其大小和方向还满足运动的初始条件，并有一组惟一的值，称为质点系的一组实位移，而称为质点系的一组广义实位移。

2虚位移--位置函数的变分虚位移是质点系在某瞬时发生的一切为约束允许的微小位移，可用位置函数的变分表示。

(8-5)与实位移不同，虚位移是约束许可的，与主动力和运动初始条件无关的，不需要经历时间的假想微小位移。

在某一时刻，质点的虚位移可以有多个。

系统静平衡时，实位移不可能发生，而虚位移则只要约束允许即可发生。

是质点系的一组虚位移，而称为质点系的一组广义虚位移。

在定常约束下，实位移一定是虚位移中的一个。

如图8.6所示单摆，虚位移可为和，而实位移仅为其一。

但在非定常约束下，实位移一般不可能是虚位移中的一个，如图8.2中所示小球，其实位移中，摆长随时间变化，而虚位移是在固定时刻，摆长不变时的位移，二者显然不同。

思考8-3①试画出思考8-1图(a)中质点B以及图(b)中套筒D的实位移和虚位移。

②试画出图8.5中双摆的虚位移。

3虚位移的计算计算质点系中各点的虚位移以及确定这些虚位移之间的关系涉及质点系的位形变化，内容十分广泛。

这里主要针对定常完整约束的刚体系统，介绍通常采用的几何法与解析法。

例8.1试确定图所示曲柄连杆机构中，A，B两点虚位移之间的关系。

解①几何法。

此处可用求实位移的方法来确定各点虚位移之间的关系。

15 理论力学--虚位移原理及其应用

15 理论力学--虚位移原理及其应用

(i = 1, 2,⋯, n )
O θ1 l1 M1(x1，2) y θ2 y l2 M2(x2，y2) x
如图15-5所示双摆。质点系由两个 质点组成，受到两个几何约束，广义坐 标数（或自由度数）为 2 ，可以选取角
ϕ 1和 ϕ 2作为广义坐标， ϕ 1和 ϕ 2相互
独立。
图 15-5
15.2.4 虚位移分析 15.2.4.1 几何法 应用几何学或运动学的方法求各点虚位移间的关 系。首先根据系统的约束条件，确定自由度，给定虚 位移，画出虚位移图，然后应用运动学的方法求有关 点虚位移间的关系。 质点的无限小位移与该点的速度成正比，即dr = v dt。 两质点无限小位移大小之比等于两点速度大小之比。 两质点虚位移大小之比等于对应点虚速度大小之比。 可以应用运动学中的速度分析方法（如瞬心法、速度 投影法、速度合成定理等）去建立虚位移间的关系。
本章重点 虚位移、理想约束的概念，应用虚位移原理 求解物体系的平衡问题。 本章难点 广义坐标、广义力的概念，广义坐标形式的 虚位移原理。
15.1 约束及其分类 . 15.1.1 约束与约束方程 位形（Configuration）： 位形 质点系内各质点在空间的位置的集合。 约束（Constraints）： 约束 在非自由质点系中，那些预先给定的限制质点系 位形或速度的运动学条件。 例如，限制刚体内任意两点间的距离不变的条件 ，限制车轮在直线轨道上滚动而不滑动的条件 约束方程（Contraint equations）： 约束方程 限制条件的数学方程式。
f j ( x1 , y1 , z1 ; ⋯; xn , yn , zn ) = 0
( j = 1, 2,⋯, s )
（15-3）
15.2 虚位移与自由度 . 15.2.1 虚位移 质点或质点系在给定位置（或瞬时），为约束所 容许的任何无限小位移，称为质点或质点系在该位置 的虚位移 虚位移（Virtual displacement）。 虚位移 虚线位移：δ r ， δ r = δ x i + δ y j + δ z k 。 虚角位移：δϕ ， δθ 。

第十五章虚位移原理

第十五章虚位移原理
F 2l δφ
F'
B
A
W
FN s 2Fl 0


2π
s
h
h s 2π
δs FN
FN h W (2Fl 2π ) 0
FN h 2 Fl 0 2π
1 FN 4π Fl h
例题
第15章 虚位移原理
例 题 1
例题
第15章 虚位移原理
2 1 2 1
2
2 1
y
x22 y22 l32 ( x1 x2 ) ( y1 y2 ) l
2 2 2
l2 m1
m2 （x ，y ） 2 2
l3 x
l1
（x1，y1）
例3：曲柄连杆机构 约束方程为：
2 2 xA yA r2
y

r φ
A （xA，yA） l
B x （xB，yB）
xC
xC
例题
第15章 虚位移原理
例 题 7
已知图所示结构，各杆都以光滑铰链连接，且有 AC=CE=BC=CD=DG=GE=l。在点G作用一铅直方向的力F，求 支座B的水平约束反力FBx。
sin ( ) M FAr cos FB r 0 cos
例：图示平面等腰三角形机构，在C点作用主动力P,系统 处于平衡，求A、B两处的约束反力。
A、B两处共有4个反力，应逐个求之。 先求哪个反力，则解除该方向的约束，代 之以对应的反力。暂时不求的则不要解除， 仍保持原约束的性质。
力学小魔术
一根重为F的均质杆简支于A,B支座上，支座的反力 分别为F/2。如果突然将支座B撤去，显然在重力矩 作用下AB杆将绕A点顺时针转动而掉下。现在，允 许在AB杆上采取一些措施，但不能对系统施加绕A 点的外力矩，使得在支座B撤去后，AB杆仍能维持 水平而不掉下。你能做到吗？

虚位移原理

虚位移原理

1 1 3 2 Q Q M 0 2 2 4 l
FA 850 N

P
Q
Q
M
rE
A B C D
若求 E处支座反力, 则 系统的虚位移分析如 图示.
FE
l 4
E
q=400N/m , P = 200N .
M = 200 m.N . l = 8m
l 8
l 8
l 8
l 8
l 8
第十五章 虚位移原理
虚位移的英文名词是 virtual displacement . 意 思是‘ 可能的位移’. 不管是‘ 虚’ 也好, 还 是‘ 可能 ’ 也好, 它的力学含义是: 仅为约束 条件所允许的位移.
引言
质点被约束在某一平面上, 其 上有力的作用.
显然, 在此平面上有无限多为 约束所允许的 位移.
FBx B F1'yC F1yG FyG 0
式中 F1 = F1'= kδ0
2 FB l sin k 0 l cos 3k 0 l cos 3 Fl cos 0 FB 3 Fctg k 0 ctg 2
F1
y
在图示坐标下 E
D
F1'
k
yG 3l sin yC l sin x B 2 l cos
ix
·C A θ θ B
( F
FB
x
x i Fiy yi ) 0
yG 3l cos yC l cos x B 2l sin
f ( xi , yi , zi ) 0 或
f ( x, y, z ) 0
2. 虚位移
定义: 在给定瞬时, 质点系在约束条件允许下所能实现的任意假想 的无限小的位移.

15虚位移原理

15虚位移原理
第15章 虚位移原理
第15章
虚位移原理
返回总目录
15.1
第15章 虚位移原理
本章内容
•约束、自由度和广义坐标 •虚 位 2
第15章 虚位移原理
15.1 约束、自由度和广义坐标
一、约束与约束方程
一质点系不受任何限制可在空间作自由运动，这样的质点系称为自由质 点系；若质点系中各质点的位置和运动受到一定限制，则称此质点系为非自 由质点系。限制质点或质点系位置和运动的各种条件，称为约束，这些限制 条件用数学方程表示出来，称为约束方程。根据约束的形式和性质，约束可 分为如下几类： 1. 几何约束和运动约束 只限制质点或质点系在空间的几何位置的约 束称为几何约束。例如图15.1所示的无重刚杆为 摆杆的单摆，其中质点M可绕固定点O在平面Oxy 内摆动，摆长为l。由于刚杆OM的限制，质点M 必须在以点O为圆心、以l为半径的圆周上运动。 若以x、y表示质点的坐标，则其位置坐标必须满 足条件 2 2 2 x y l
π F rB co s P rC 0 2
P C θ θ A
①
B
δr δrB
F
C
由速度投影定理，BC杆上任意两点的速度在此两 点连线的投影相等，B、C两点的虚位移在BC连线上 的投影也应该相等，由图有
π π rC co s rB co s 2 2 2
F i ri F N ri 0
i
对于质点系内所有质点，都可以得到与上式相同的式子。将所有等式两 边分别相加，得
F
i
r
i
F
i
Ni
r 0
i
由于质点系具有理想约束，则约束反力在虚位移中所作的虚功为零，即， 代入上式得 Fi r 0 于是得

虚位移原理

虚位移原理
和 FB 作用点的虚位移，如图所示。 因 AB 是刚杆，两端位移在 AB 上
的投影应相等，即
|rA | sin ( ) |rB | cos
可见 A，B 两点的虚位移大小之比等于
|rA | cos |rB | sin ( )
根据虚位移原理的平衡方程，有
W FA | rA | FB | rB | 0
yB
d
cos2
yC yB
O
例题4
y l B
θ
FA A
rA
rB x
C d
FC rC
38
例题
虚位移原理
例题4
应用虚位移原理得 y
W FA sin xA FA cos yA FCyC 0
(FAl
sin
2
FAl
cos2
Fc d
cos2
)
0
O
因 0 ，故有
FC
l d
cos2
FA
l B
θ
d FC
)
0
y MAA φ
δφ
F1 F2 FG
B
C
F3
H E
D
因广义坐标的独立变分δφ为任意微量
δyF1
δyG1 δyD1 δyH1
0
δyB1
故
MA
2F1
8 3
F2
4 3
F3
1867
N m
44
例题
虚位移原理
例题5
2. 为了求出固定端A的约束力FA， 应将A端约束换成铅直滚轮，而把固定 端的铅直约束力FA视作为主动力。
三、虚位移
在质点系运动过程的某瞬时，质点系在约束允许的条件 下，可能实现的任何无限小位移，称为质点系（在该瞬时） 的虚位移。

6理论力学---第十五章虚位移原理

6理论力学---第十五章虚位移原理
34
[例6]
滑套D套在光滑直杆AB上，并
带动杆CD在铅直滑道上滑动。已知
=0o时，弹簧等于原长，弹簧刚度系数
三、虚功
力 F 在质点发生的虚位移 r 上所作的功称为虚功，记为W。
W F r W Xx Yy Zz
20
理想约束
如果在质点系的任何虚位移上，质点系的所有约束反力的
虚功之和等于零，则称这种约束为理想约束。
质点系受有理想约束的条件：
WN N i ri 0
rG rG rE rG FG 2 rE rB rB FG 4 r r 4 3 rB 4rB E B r 1 1 11 11 1 r E C 12 rB 12 8 96 6 rB
11 P 11 m RB 1 P 2 1 8 2 96
18
2、解析法 将C、A、B点的坐标表示成 广义坐标 的函数，得
xC acos , yC asin x A l cos , y A lsin x B 2acos , y B 0
对广义坐标 求变分，得各点 虚位移在相应坐标轴上的投影：
xC asin , yC acos x A lsin , y A l cos x B 2asin , y B 0 19
1、约束 限制非自由质点（或质点系）运动的各种条件称为约束。 将约束的限制条件以数学方程来表示，则称为约束方程。
例如：
x2 y 2 l 2
平面单摆
4
曲柄连杆机构
x A2 y A2 r 2
( xB x A ) 2 ( y B y A ) 2 l 2
yB 0
约束的分类 根据约束的形式和性质划分为不同的类型

理论力学15-2虚功原理N

理论力学15-2虚功原理N
1 x B yC tan 2 1 [ FCy F ( tan )]yC 0 2 δyC 是任意的，∴ 1 FCy F tan ( ) 2
F
x B
y
x
若用几何法分析虚位移： 几何法分析虚位移，无需 对AB 杆，δrB方向如图， 设定坐标系。 由协调关系，δyC方向如图。 两虚位移在BC杆方向投影应相等： rB cos(2 90) rC cos(90 ) rB sin 2 rC sin 两虚位移关系： rC 2rB cos 用虚功方程 (FCy视为主动力) FCy (rC ) F (rB cos(90 )) 0
2 rD rE 3
3 r2 rE 4
四) 用虚功方程 ( Fi ri ) 0 10 r1 FD (rD ) 6 r2 3(- ) 0 3rE rE rE 2rE rD r1 r2
3 3 6 4 1 2 3 1 [10 FD ( ) 6 3( )]rE 0 3 3 4 6 FD 11(kN ) ( )
四、虚位移原理应用
一) 用虚位移原理求平衡位置的主动力
基本步骤： 1. 受力分析 画出全部可作虚功的主动力； 2. 虚位移分析 1) 变分法：建坐标系，列出虚位移点的坐标， 进行变分计算，建立虚位移之间的关系。 2) 几何法：根据虚位移的协调关系及虚位移的 投影关系，建立虚位移之间的关系。 3. 使用虚位移原理：
若求B点约束反力，虚位移图？
若求A点约束反力，虚位移图？
二) 用虚位移原理求平衡时的约束反力 虚位移原理是作用于质点系上所有主动力在任 何虚位移中所作虚功之和为零。 它与约束反力无关，似乎无法求约束反力。 若用该原理求约束反力，可沿所求约束反力方 向解除相应约束，并用一假想的主动力代替。 再用虚位移原理，求出该假想施加的“主动 力”，仍可得到对应的约束反力。

第15章虚位移原理例题

第15章虚位移原理例题

已知ctgθ=2。
解：将杆BD截断，暴露出内力
F
、F
给出力
P
、
F
处的虚位移 rD、rB
几何法： rC cos rD
C
rC cos(90 2 ) rB cos
A
θ
θ rC D F Fθ
rB
B
由虚功原理 PrD FrB 0 0
PrC cos F 2sinrC 0 (P cos 2F sin )rC 0
P
rD
F P ctg P
2
FNB
P1
Hale Waihona Puke r1 rBP2rC rB
M
rB
FNB
P1
r1 rB
P2
rC rB
M
rB
M
FNB
而
r1 rB
1 2
,
rC rB
181
,
rB
rG
4
1rB
rE
6
1rB
rC
12
1rB
1 12
181
11 96
FNB
1 2
P1
11 8
P2
11 96
M
例11： 书15-15
用虚位移原理求图示桁架中杆BD的内力，
例9：三铰拱上有载荷作用力P及力偶M， 各尺寸如图，求B铰的约束力。 解：（1）求B 铰水平约束力：
解除B 铰的水平约束，代之以水平力FBx 分析主动力：M，P，FBx ，
给虚位移，求虚位移关系：
C*为刚体CDB的瞬心，
刚体CDB的虚转角也为 。 rD a (1)
rB 2a (2)
列虚功方程：
re
300
cos

理论力学-虚位移原理

理论力学-虚位移原理
而虚位移原理则将利用后一种情况，他通过主动力在 约束所许可的位移上的表现（通过功的形式）来给出质点 系的平衡条件。
因此，在虚位移原理中，首先要研究加在质点系上的 各种约束，以及约束所许可的位移的普遍性质。
第六章 虚位移原理
§6-2 约束和约束方程
约束与约束方程 约束的类型
第六章 虚位移原理
§6-2 约束和约束方程
式中xA，yA和xB，yB分别为A，B两点的直角坐标。上述方程表明这四 个坐标并非都独立。可以消去其中的某三个，从而只剩下一个独立坐标，
这一坐标完全确定了此质点系的位置。
以后我们改称系统的位置为位形。
第六章 虚位移原理
§6-2 约束和约束方程
约束实例
曲面
图示质点A在曲面上运动，质点A的约束方程就是曲面 的曲面方程：
z
f (x, y, z) 0
A（x, y, z)
z
y
x
x
y
第六章 虚位移原理
§6-2 约束和约束方程
约束类型
三、约束的类型
按照约束对质点系运动限制的不同情况，可将约束分类如下：
1.完整约束和非完整约束
其约束方程的一般形式为
f j (x1, y1, z1; ...; xn , yn , zn; x1, y1, z1, ...; xn, yn, zn; t) 0
约束类型
第六章 虚位移原理
非完整约束
§6-2 约束和约束方程
约束类型
2.定常约束和非定常约束
● 如果约束方程中不含时间t，这种约束称为定常约束或稳 定约束。
定常约束一般形式为
f j (x1, y1, z1; ...; xn, yn, zn; x1, y1, z1,...; xn, yn, zn;) 0

理论力学虚位移原理

理论力学虚位移原理

Y
AB
X
特殊力系做功的计算
1、汇交力系合力做功
合力主矢 FR Fi
W FR dr Fi dr Fi dr Wi
AB
AB
AB
合力在有限路径做功等于分力在有限路径上做功之和
2、内力做功 内力的特点：成对出现，大小相等，方向相反
设两个质点M1， M2 相互作用力F12 ，F21
dr
由于约束力作用线与位移方向
恒垂直，因此做功恒等于零。
N
光滑铰链约束
固定铰约束点处位移恒等于零，因此做功恒等于零； 活动铰可移动方向约束力恒垂直，因此做功恒等于零。
中间铰处约束力做功恒等于零——自行分析
凡是约束反力做功恒等于零的约束称为理想约束
有势力做功
有势力——做功仅与力作用的起止位置有关而与移动路径无关。
自由度和广义坐标
自由度：描述在几何约束条件下质点系位形的独立参变 量的个数。
对于n个自由质点组成的质点系，可用3n个直角坐标（xi ，yi，zi）
i=1，2，3…n，描述每一个质点所在的位置称为质点系的位形。整
个系统有3n个自由度。
对于n个质点组成的非自由质点系，设其有S个约束方程，表明描 述质点系位形的3n个直角坐标不独立。这时，可以选取独立的k个 参数表示质点系的位形，而
k 3n S
设 q1, q2 qk 为描述系统位形的独立参数，称为广义坐标。
两个质点组成质点系
Z
(x2 , y2 , z2 )
约束方程
(x1 x2 )2 ( y1 y2 )2 (z1 z2 )2 l 2
Y
自由度数 k 3 2 1 5

(x1, y1, z1)

理论力学练习册及答案

理论力学练习册及答案
解：动点取杆OA上A点，动系固连杆O1C上，定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理 作加速度图。
取 方向投影，得：
再取动点杆O1C上C点，动系固连套筒B上，定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理:
作加速度图。
取 方向投影，得：
取 方向投影，得：
第八章 刚体平面运动
8-1.已知图示机构滑块B，沿水平方向按规律SB=0.01t2+0.18t m移动，通过连杆AB带动半径R＝0.1 m的轮子沿水平方向只滚不滑。求当t=1 s时，点A和点C在图示位置的速度和加速度。
解：当 时，
由于杆AB作瞬时平动，且P为轮C
的速度瞬心，故有：
8-2.曲柄OA=17 cm，绕定轴O转动的角速度ωOA=12 rad/s，AB=12 cm，BD=44 cm，滑块C、D分别沿着铅垂与水平滑道运动，在图示瞬时OA铅垂，求滑块C与D的速度。
2、研究滑块A运动副，求 ,
3、分别作套筒o运动副、滑块A运动副
加速度图，
4、研究杆BE，作O、A加速度图，
5、分别列O、A点加速度投影式求解
7-7.圆盘半径OA=r，可绕其边缘上一点A转动，从而带动直杆BC绕B点转动，AB=3r，且直杆与圆盘始终相切，当圆盘中心运动到AB连线上时，圆盘转动的角速度为ω，角加速度为ε，求此瞬时直杆BC的角速度和角加速度。
8-5.滑块B、D在铅直导槽中滑动，通过连杆BA及CD与轮子A相连，各连接处都是光滑铰链。轮A放在水平面上，AB=10 cm，CD=13 cm。在图示瞬时，即轮心A至两铅垂导槽的距离均为8 cm时，可在水平面上自由滚动的轮子，其轮心速度νA=30 cm/s，方向水平向右。求此时滑块D的速度。

理论力学第十五章虚位移原理

理论力学第十五章虚位移原理

将约束的限制条件以数学方程来表示，则称为约束方程。

平面单摆
2
22l y x =+：
曲柄连杆机构
2
22r y x A A =+ , )()(222=-+-A B A B y l y y x x 当约束条件与时间有关，并随时间变化时称为非定常约束定常约束。

前面的例子中约束条件皆不随时间变化，它们都是定常约束。

由一条穿过固定圆环的细绳刚杆
x 2+y 2=l 2
绳
x 2+y 2≤l 2
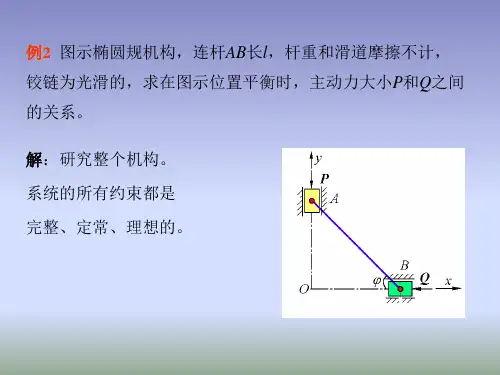
§15-2sin sin 21a x a x ==M
δϕδϕ对广义坐标ϕ求变分，得各点虚位移在相应坐标轴上的投影：
cos ,sin cos ,sin ⋅=⋅⋅=⋅C l y l a y a δϕϕδδϕϕδϕϕδδϕϕ2、光滑铰链
、无重刚杆'⋅+⋅=r N r N W N δδδ=⋅=r N W N δ，y
)(
0a )cos 2sin 2=+δψψψb F b ψδψϕδϕcos 2b +
)=δϕϕ0
2=--δθδm r P C B
B C B r m r r P r r δδθδδδ++21
8111211121614 , 8
11 , 21
1⨯=⋅=⋅=⋅===B C B E B G B C B r r r r r r r r r r δδδδδδδδδδ11111：这是一个已知系统平衡，求作用于系统上主动力之间关系的问题。

将弹簧力计入主动力，系统简化为理想约束系统，故0
] tg sec =δθθθ
力可选束反
只解由。

虚位移原理习题解答

虚位移原理习题解答

7－1. 在图示机构中，曲柄OA 上作用一力偶，其矩为M ，另在滑块D 上作用水平力F 。

机构尺寸如图所示。

求当机构平衡时，力F 与力偶矩M 的关系。

解 设OA 杆虚位移为δϕ，则A 、B 、C 、D 各点虚位移如图，θδθδθδθδδϕδcos 2cos cos 2cos D B A B A r r r r a r ===由上述各式和虚功方程0=+-D r F M δδϕ解出θ2tan Fa M =7－2. 图示桁架中，已知AD=DB=6m ，CD=3m ，节点D 处载荷为P 。

试用虚位移原理求杆3的内力。

解 B 、C 、D 各点虚位移如图所示，θδδθδθδcos ,2sin cos C D c B r r r r ==代入虚功方程 03=-B D r F r P δδ解得杆3的内力 P PF ==θcot 23 7－3. 组合梁由铰链C 铰接AC 和CE 而成，载荷分布如图所示。

已知跨度l=8m ，P=4900N ，均布力q=2450N/m ，力偶矩M=4900N ⋅m ；求支座反力。

N 2450N 14700N 2450==-=E B A F F F ，，7－4 组合梁由水平梁AC 、CD 组成，如图所。

已知：F 1= 20kN ，F 2 = 12kN ，q = 4kN/m ，M = 2kN ·m 。

不计梁自重，试求：固定端A 和支座B 处的约束力。

组合梁由水平梁AC 、CD 组成，如图12－16a 所。

已知：F 1= 20kN ，F 2 = 12kN ，q = 4kN/m ，M = 2kN ·m 。

不计梁自重，试求：固定端A 和支座B 处的约束力。

(a)(b)2 222(d )(e)图12－16 例题12－5图解：组合梁为静定结构，其自由度为零，不可能发生虚位移。

为能应用虚位移原理确定A 、B 二处的约束力，可逐次解除一个约束，代之以作用力，使系统具有一个自由度，并解除约束处的正应力视为主动力；分析系统各主动力作用点的虚位移以及相应的虚功，应用虚位移原理建立求解约束力的方程。

第十五章 虚位移原理(Y)

第十五章 虚位移原理(Y)

作用力和运动的初始条件。
非自由质点系——质点系的运动状态受到某些预先给定的限制。 （运动的初始条件也要满足这些限制条件）
1、约束及约束方程
约束——非自由质点或质点系受到的预先给定的限制。
约束方程——将约束的限制条件以数学方程式表示出来。
曲柄连杆机构
平面单摆
x A2 y A2 r 2
2
yB 0
x y l
2
2
( xB xA )2 ( yB y A )2 l 2
2、约束的分类
根据约束的形式和性质，可将约束划分为不同的类型， 通常按如下分类：
（1）几何约束
限制质点系在空间几何位置的条件称为几何约束。 几何约束方程的一般形式为:
f r ( x1 , y1 , z1 , , xn , yn , zn ) 0
三、虚位移原理
1、虚位移原理
具有双面、定常、理想约束的质点系平衡的充要条件是： 作用于质点系的所有主动力在任何虚位移上所作的虚功
之和等于零。
Fi ri 0
用几何法表示为：
Firi cosi 0
用解析式表示为：
(F
xi
xi Fy iyi Fzi zi ) 0
即各质点虚位移之比等于各质点速度之比。
v A rA vB rB
刚体平动
r1 r2 rn rC
刚体绕定轴转动
v1 v2 vn vC
vA AC vB BC vD DC
rA AC
rB BC
x2 y 2 (l0 vt)2
x2 y 2 l 2
（4）双面约束和单面约束

虚位移原理——精选推荐

虚位移原理——精选推荐

虚位移原理虚位移原理提供了静力学问题的一种全新的解法，它还是分析力学的基础。

虚位移原理是设计用来消除平衡方程中的约束力，主要是用来求解平衡系统的主动力之间的关系或平衡位置。

另外，通过解除约束，将内力或约束力转化为主动力，则虚位移原理也可用来求解内力和约束力，而且这比以前的列平衡方程的常规方法更有效。

一、力的功元功：力在微小位移上所做的功称为元功。

其数学表达式为：t d W v F ∙=δ或r F d W ∙=δ，其中v 和r d 分别为力F 作用点的速度和微小位移。

变力在曲线路径上做的功可以用曲线积分计算。

等效力系做功定理: 等效力系在刚体的位移上所做的功相等。

即：若},,{},,{11m P P F F n =，则∑∑===mj jn i i P W F W 11)()(。

在计算力的功时，为计算方便，可以利用上述定理。

例如：图4-1(a)所示鼓轮上缠绕有柔索，在力F （大小和方向不变）作用下在地面上纯滚动。

计算在轮心沿直线移动S 距离过程中力F 所做的功。

(a) (b) 图4-1由于力F 的作用点的位移不易计算，我们可将F 平移到轮心，同时附加一力偶M (其力偶矩的大小为=M Fr ,如图4－1b 所示）以保持力系等效，即},{}{M F F =。

新的力系},{M F 在轮心沿直线移动S 距离过程中所作的功较易计算：ϕθM FS W +=cos ，其中：ϕ为圆盘轮心移动S 距离时，圆盘转动的角度，即RS ＝ϕ，于是上式可写成cos SW FS Fr R θ=+⋅ 它等于在轮心沿直线位移S 距离过程中力F 所做的功。

返回主目录二、约束及其分类约束：对质点或质点系运动所加的限制。

如某质点被限制在固定曲面上运动,则该质点就是受到了约束。

约束体对被约束体的运动是通过力的作用(称为约束力)来加以限制的,但是约束与受力是应区别对待的两个不同概念,这可以通过下面的例子来区分.(a)(b) (c)图4-2对图4-2中所示的系统：在(a)中，质点A 被固定在刚性杆上并球铰链连接接在固定点o 。

理论力学12—虚位移原理(选讲)

理论力学12—虚位移原理(选讲)
y A
j
d rA
dj
l
可得
δrB vB BC sin(j ) δrA vA AC cos

O

x
d rB
B
2. 解析法
解析法是利用对约束方程或坐标表达式进行 变分以求出虚位移之间的关系。例如
椭圆规机构如图, xA, yA坐标有约束方程
x y l
2 B 2 A
2
y dyA A(xA, yA)
由于d≠0, 于是得
FA 2FB tan
例: 图示机构中, 当曲柄OC绕轴摆动时, 滑块A沿曲柄 自由滑动, 从而带动杆AB在铅垂导槽内移动。求机构 d rC 平衡时力F1与F2的关系。 解1: (几何法)以系统为研 C d r A 究对象 , 受的主动力有 F1 、 F1 y F2。给系统一组虚位移如 A d j 图。
只能限制质点某方向的运动 , 而不能限制相反 方向运动的约束称为单面约束(非固执约束)。 其约束方程的一般形式为
f j ( x1, y1, z1, , xn , yn , zn ) 0
15.1.1 约束类型及分类 四、完整约束与非完整约束 如果约束方程中不包含坐标对时间的导数 , 或 者约束方程中的微分项可以积分为有限形式 , 这类约束称为完整约束。 如果在约束方程中包含坐标对时间的导数 , 并 且方程不可能积分为有限形式 , 这类约束称为 非完整约束。
y

yA r
0
运动约束方程的一般形式为
C
f j ( x1, y1, z1, , xn , yn , zn , x1, y1, z1, , xn , yn , zn ) 0
15.1.1 约束类型及分类 二、定常约束与非定常约束 约束条件不随时间变化的约束称为定常约束。 在定常约束中不显含时间t。 约束条件随时间变化的约束称为非定常约束。

虚位移原理应用功的概念分析系统的平衡问题

虚位移原理应用功的概念分析系统的平衡问题

第十五章虚位移原理§15－1 约束•虚位移•虚功§15－2 虚位移原理§15－3 应用举例虚位移原理应用功的概念分析系统的平衡问题，是研究静力学平衡问题的另一途径。

1．约束及分类约束：限制质点或质点系运动的条件称为约束。

表示这些限制条件的数学方程称为约束方程。

（1）几何约束和运动约束几何约束：限制质点或质点系在空间的几何位置的条件。

如图1所示的平面单摆，其约束方程可表示为§15－1 约束•虚位移•虚功o yx),(yxA图1222lyx=+又如图2所示的曲柄连杆机构，其约束方程则为222ay x AA =+222)()(by y x x A B A B =-+-0=B y 运动约束：约束对质点或质点系的运动进行限制的条件。

如车轮沿直线轨道作纯滚动，如图3所示。

Oyxba),(A A y x A ),(B B y x B 图2ωrv o yx图3ry =000=-ωr v )0(0=-ϕ&&r x 其几何约束为运动约束为（2）定常约束和非定常约束定常约束：约束条件不随时间改变的约束。

如图1、2、3中各例的约束条件皆不随时间变化，它们均是定常约束。

非定常约束：约束条件随时间而改变的约束。

如图4所示，重物由一条穿过固定圆环的细绳系住。

设初始摆长为，匀速拉动绳子。

其约束方程为M 0l v oyx ),(y x M lvϕ图42022)(vt l y x -=+方程中显含时间，此约束为非定常约束。

t（3）完整约束和非完整约束完整约束：这类约束的约束方程中不包含坐标对时间的导数，或者方程中的微分项可以积分为有限形式。

如图3中，运动约束方程虽是微分形式，但可以积分为有限形式，故为完整约束。

00=-ϕ&&r x 非完整约束：这类约束的约束方程中包含坐标对时间的导数（如运动约束），且方程不可积分为有限形式。

（4）单侧约束和双侧的约束单侧约束：只能限制质点或质点系单一方向运动的约束。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第15章 虚位移原理
15-2 图示曲柄式压榨机的销钉B 上作用有水平力F ，此力位于平面ABC 内。

作用线平分∠ABC 。

设AB=BC ，∠ABC=θ2，各处摩擦及杆重不计，求对物体的压缩力。

解： （1）取整个系统为研究对象 （2）受力分析
拆掉被压榨物体，用力D F
代替。

此时主动力为：D F F ,
，约束为理想约束。

（3）给虚位移求关系D B r r
δδ,
C B ,点虚位移在BC 连线上投影相等：
)90cos()902cos(0θδθδ-=-D B r r 即：D B r r δθδ=cos 2 （4）由虚位移原理：
0)90cos(0
=--D D B r F r F δθδ 代入虚位移关系： θF t g F D 2
1
=
15-3在图示机构中，当曲柄OC 绕O 轴摆动时，滑块A 沿曲柄滑动，从而带动杆AB 在铅直导槽K 内移动。

已知：OC=a ，OK=l ，在点C 处垂直于曲柄作用一力F 1；而在点B 沿BA 作用一力F 2。

求机构平衡时F 2与F 1的关系。

解：
（1）取整个系统为研究对象 （2）受力分析 主动力为：21,F F
，约束为理想约束。

（3）给虚位移求关系C A r r δδ, 虚位移满足合成关系：r A e A A r r r δδδ+=
ϕδδcos A e
A r r =
A A e A C r l a a l r OC OA r r δϕϕϕδδδ⋅=⋅=⋅=2cos cos /cos
（4）由虚位移原理：
012=-C A r F r F δδ 0cos 212=⋅-A A r l
a F r F δϕδ
则：l a F F ϕ2
12cos =
1
1
15-4 在图示机构中，曲柄OA 上作用一力偶，其矩为M ，另在滑块D 作用水平力F 。

机构尺寸如图所示。

求当机构平衡时，力F 与力偶矩M 的关系。

解：
（4）取整个系统为研究对象
（5）受力分析
主动力为：M F ,
，约束为理想约束。

（6）给虚位移求位移关系 D B r r δδ,在BD 连线上投影相等：
θδθδcos )902180cos(00D B r r =-- 即： D B r r δθδ=sin 2 A B r r
δδ,在AB 连线上投影相等：
即：θ
θ
δδcos 2cos B A r r =
（4）由虚位移原理：
0=+-a
r M
r F A
D δδ
0cos 2cos sin 2=⋅+
⋅-θ
θ
δθδB B r a M r F
θ2cot a
M
F =
15-5 如图所示两等长杆AB 与BC 在点B 用铰链连接，又在杆的D 、E 两点连一弹簧。

弹簧的刚性系数为k ，当距离AC=a 时，弹簧内拉力为0。

如在点C 作用一水平力F ，杆系处于平衡，求距离AC 之值。

解：
（7）取整个系统为研究对象 （8）受力分析 弹簧用力代替
主动力为：E D F F F
,,
x l b DE = )()(a x l
kb
a l
b x l b k F F E D -=-==
约束为理想约束。

（9
θθθ
cos 2cos )(cos )(l x b l x b l x C E D =+=-= θδθ
δθδθδθδθ
δsin 2sin )(sin )(l x b l x b l x C E D -=+-=--=
（4）由虚位移原理：
0=-+E E D D C x F x F r F δδδ
0sin )()(sin ))((sin 2=+-+---⋅-θδθδθδθθδθb l a x l kb
b l a x l kb l F
则：22kb
F
l a x +=
x
15-6 图示桁架中，已知AD=DB=6m ，CD=3m ，节点D 处载荷为P 。

试用虚位移原理求杆3内力。

解： 将3杆截断，用内力代替 （10） 取整个系统为研究对象 （11） 受力分析 弹簧用力代替
主动力为：'33,,F F P 而：'
=33F F 约束为理想约束。

（12） 给虚位移和虚位移关系 B C D r r r δδδ,, D D
C r r r δδδ2
536622=+⋅= BC 为平面运动构件，B C r r
δδ,满足：
αδαδcos )290cos(0
B C r r =- 则：αδδsin 2C B r r =
2163==
αtg 则：D B r r δδ=
（4）由虚位移原理：
03=-B D r F r P δδ 03=-D D r F r P δδ 则：P F =3
B。