当前位置：文档之家 › 第四章 根轨迹法 习题

第四章 根轨迹法 习题

  • 格式：doc
  • 大小：110.50 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

自动控制原理简明教程 第四章 根轨迹法 习题答案

自动控制原理简明教程 第四章 根轨迹法 习题答案
另一个闭环极点为 S3 ，则
(S S3 )(S 1)2 S (S 3)2 4
则解得：
(S S3 )(S 1)2 S (S 1)2 4(S 1)2 (S 4)(S 1)2
则 (S S3) S 4 S3 4 （另外一个闭环极点） 临界阻尼时的闭环传递函数为
(S)
(S
4(S 1) 4)(S 1)2
d d 2 d 1 j d 1 j
n
(
1
m
1 ) 求分离点的坐标公式
i1 d Pi i1 d Zi
解得：d 1
分离角： l
180 l
180 2
900
此时对应为T值：
（应使用模值方程求得）
T S S2 1T 1
S 1 j S 1 j
P1(-1,j)
T=0
Z2
Z1
-2
-1
0
T=∞
传递函数（写成零极点乘积形式） 解：系统结构图如下：
R(S) -
G(S)
C(S)
如果没有特别强调是正反馈，则单位反馈系统都 是单位负反馈系统。该题为参量根轨迹。 根轨迹方程：1 G(S) 1 4(S k) 0
S(S 1)(S 5)
特征方程：
D(S) S 3 6S 2 9S 4k 0
等效开环传递函数为：
G开 (S)
4k S(S
3)2
1
4k S (S 3)2
0
开环零点： m 0
开环极点： n 3, P1 0, P2 3, P3 3 则根轨迹有3条分支，有3条渐近线。
根轨迹与实轴的交点：
n
m
a
Pi Zi
i 1
i 1
nm
3 3 2 3
渐近线与实轴正方向夹角

第四章根轨迹法4-2

第四章根轨迹法4-2

P( s )Q( s ) P( s )Q( s ) 0
即 其中
P( s ) Q( s ) P( s ) Q( s )
d [ln P(s)] d [ln Q(s)]
ds
ds
P(s) (s z1 )(s z2 ) (s zm )
Q(s)- (s p1 )(s p2 ) (s pn )
的 j 值。工作在此点时，系统处于临界稳定状态。
介绍二种常用的求交点的方法。 (1) 利用特征方程求取。用 j 替代s，令虚部、实部分别等
于 零，求得 和对应的K1。 (2) 利用劳斯表求取。将劳斯表中s2行系数构造的辅助方程
求得。若根轨迹与虚轴的交点多于两个，则应取劳斯 阵列中大于2的偶次方行的系数构造的辅助方程求得。
i1
ib
8 虚轴交点 （1）满足特征方程 1 G( j)H( j) 0 的 j 值；
（2）由劳斯判据求临界稳定时的特征根；
9
根之和与 根之积
n
pcj
n
p
j
j 1
j 1
n
j 1
pcj
1
n
n
j 1
pj
K1
m
i 1
zi
19
例1: 系统的开环传递函数 试画根轨迹。
G(s)H(s)
K1
s(s 4)(s 6)
ω4 -36ω2 K0 jω80 - 8ω2 0
ω4 -36ω2 K0 0
jω80 - 8ω2 0
求得 ω 10 , K0 260
( (4)出射角
极点-p3的出射角 ： 3 180 (2k 1) (2 90 180 2 ) 90
同理不难求得极点-p4处的出射角： 4 90

自控原理第四章书后习题答案

自控原理第四章书后习题答案

4-1 绘制具有下列开环传递函数的负反馈系统的根轨迹1、()()()()54*++=s s s K s H s G解：（1）3个开环极点为：p 1=0，p 2=-4，p 3=-5。

（2）实轴上的根轨迹（-4，0），（-∞，-5）（3）303054011-=----=--=∑∑==mn zp n i mj jiσ()() ,,331212ππππϕ±±=+=-+=k mn k a(4) 分离点：1110d 45d d ++=++ d=-1.47, d=-4.53(舍) （5）与虚轴的交点：在交点处，s=j ω，同时也是闭环系统的特征根，必然符合闭环特征方程，于是有：()020********=++--=+++*=*K j j K s s sj s ωωωω整理得： 0203=-ωω；092=-*ωK 解得01=ω；203,2±=ω；18092==*ωK 最后，根据以上数据精确地画出根轨迹。

2、()()()()11.02*++=s s s K s H s G 解：（1）开环极点有3个，分别为：p 1=p 2=-0，p 3=-1，开环零点为z=-0.1 （2）实轴上的根轨迹为：[-1 -0.1] (3) 渐进线有两条，45.0131.010011-=-+--=--=∑∑==mn zp n i mj jiσ()() ,23,2131212ππππϕ±±=-+=-+=k mn k a (4) 分离点：1111d 10.1d d d ++=++ d=0, d=--0.4(舍), d=0.25(舍)分离角：()() ,23,221212ππππϕ±±=+=+=k lk d 最后，精确地画出根轨迹。

4-3 已知系统的开环传递函数为()()()2*1+=s s K s H s G ① 绘制系统的根轨迹图；② 确定实轴上的分离点及K *的值； ③ 确定使系统稳定的K *值范围。

第四章 根轨迹法(1)

第四章 根轨迹法(1)

第四章 根轨迹法
（1）当 K * = 0时，s1 = 0、s2 = －2， 此时闭环极点就是开环极点。 （2）当0＜ K * ＜1时， s1 、 s2 均为负 实数，且位于负实轴的（－2，0） 一 段上。 （3）当K * = 1时，s1 = s2 = －1，两 个负实数闭环极点重合在一起。 （4）当1＜ K * ＜∞时， s1， 1 1 k * 2 两个闭环极点变为一对共轭复数极点。 s1 、 s2 的实部不随K * 变化，其位于过 （－1，0）点且平行于虚轴的直线上。 （5）当K * ＝∞时， s1 = －1+ j∞、 s2 = －1－j∞，此时s1、s2将趋于无限 远处。
第四章 根轨迹法
② 位于s1左边的实数零、极 点： (S1 – P4 ) 、(S1 – Z1 ) 、 向量引起的相角为0°
∴ 判断 s1是否落在根轨迹 上，位于s1左边的零、极点不 考虑。
③ 位于s1右边的实数零、极点： 每个零、极点提供180°相 角，其代数和为奇数，则满足相角条件。
第四章 根轨迹法
a
(0) (1 j1) (1 j1) (4) (1) 5 4 1 3
60 180 2k 1 180 2k 1 a 180 nm 3 300
k 0 k 1 k 2
第四章 根轨迹法
五、法则五 根轨迹分离点和分离角
K G( s) H ( S )
* i 1 n j 1
(s z )
i
m
S (s p j )
-1
m个开环零点 n个开环极点 K *根轨迹增益
∴在s平面上凡是满足上式的任意一个点s1、s2、…、 s∞，都 是闭环特征根，即闭环极点。
第四章 根轨迹法

根轨迹例题

根轨迹例题
4s 3 72s 2 200s 400 0
求得分离点为： （6）根轨迹的起始角：
s 15
因为开环有一对共轭复数极点，需求 p3、 4 处的根轨迹起始角。
p (2k 1) ( p3 zi ) ( p3 p j )
3
m
n
i 1
j 1 j 3
系统的大致根轨迹如图：
确定K值范围：与分离点s1相应的
K g s . s 1. s 4 s0.46 0.88
K K g 4 0.22
因此，若使系统在阶跃响应下为衰减振荡型，K的取值 范围应为 0.22 K 5 。
例2：已知控制系统前向通道和反馈通道传递函数分别为：
实部为零 虚部为零
5 6 ＝ 3
k 1391
（rad/s ）
k K 3.47 400
根据以上结果画出概略的根轨迹图。
例1：已知系统的开环传递函数为： K G( s) H ( s) s( s 1)(0.25s 1) （1）绘制系统的根轨迹图； （2）为使系统的阶跃响应呈现衰减形式，试确定K值范围。 解： 系统的开环传递函数为
K [例]开环传递函数为 Gk (s) s(0.05s 1)(0.05s 2 0.2s 1) ，试绘制系
统的根轨迹。
解：将开环传递函数写成绘制根轨迹的标准形式
k Gk ( s) s( s 20)(s 2 4s 20) (k 400K )
开环有四个极点：
p1 0 p2 20 p3、 4 2 4 j
Kg 4K G( s) H ( s) s( s 1)(s 4) s( s 1)(s 4)
其中
K g 4K

自动控制原理第四章根轨迹法

自动控制原理第四章根轨迹法

i 1
j 1
开环极点到此被测零点 (终点)的矢量相角
8. 根轨迹的平衡性(根之和） （ n-m 2）
特征方程 Qs KPs 0
sn an1sn1 a1s a0 K sm bm1sm1 b1s b0 0
n
Qs KPs s p j sn cn1sn1 c1s c0 0 j 1
i 1
j1
k 0,1,2,
s zoi i 开环有限零点到s的矢量的相角
s poj j 开环极点到s的矢量的相角
矢量的相角以逆时针方向为正。
幅值条件：
s
m
m
s zoi
li
A s
i 1 n
i 1 n
s poj
Lj
j 1
j1
li αi
-zoi
Lj βj
×
-poj
开 环 有 限 零 点 到s的 矢 量 长 度 之 积 开环极点到s的矢量长度之积
， 2 2
c 2k 11800 2
由此可推理得到出射角：
其余开环极点到被测极 点(起点)的矢量相角
n1
m
c 2k 1180o j i
j 1
i 1
有限零点到被测极点
(起点)的矢量相角
同理入射角：
其余开环有限零点到被测 零点(终点)的矢量相角
m1
n
r 2k 1180o i j
1 GsHs 0
m
GsHs
KPs Qs
K
i 1
n
s
s
zoi
poj
j 1
P s sm bm1sm1 b1s b0
Q s sn an1sn1 a1s a0
于是，特征方程

第四章 根轨迹法习题

第四章 根轨迹法习题

第四章 根轨迹法习题4-1 系统的开环传递函数为 )4)(2)(1()()(*+++=s s s Ks H s G试证明点311j s +-=在根轨迹上，并求出相应的根轨迹增益*K 和开环增益K 。

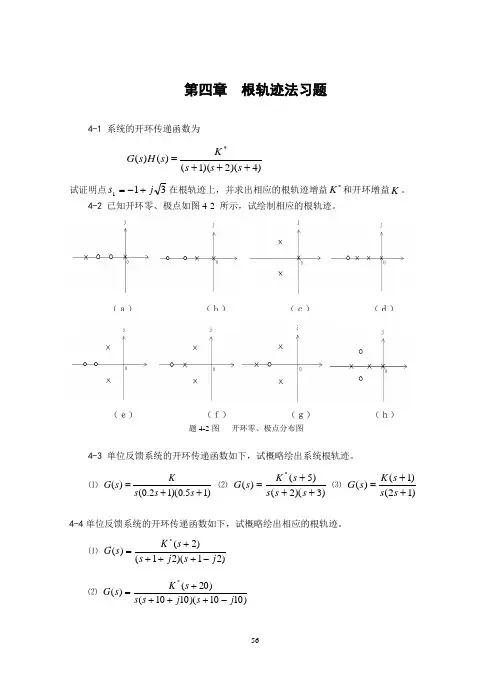
4-2 已知开环零、极点如图4-2 所示，试绘制相应的根轨迹。

4-3 单位反馈系统的开环传递函数如下，试概略绘出系统根轨迹。

⑴ )15.0)(12.0()(++=s s s Ks G ⑵ )3)(2()5()(*+++=s s s s K s G ⑶ )12()1()(++=s s s K s G4-4单位反馈系统的开环传递函数如下，试概略绘出相应的根轨迹。

⑴ )21)(21()2()(*j s j s s K s G -++++=⑵ )1010)(1010()20()(*j s j s s s K s G -++++=4-５ 系统的开环传递函数如下，试概略绘出相应的根轨迹。

⑴ )208()()(2++=*s s s Ks H s G ⑵ )5)(2)(1()()(+++=*s s s s Ks H s G⑶ )22)(3()2()()(2++++=*s s s s s K s H s G ⑷ )164)(1()1()()(2++-+=*s s s s s K s H s G4-６ 已知单位反馈系统的开环传递函数)(s G ，要求： （1）确定)20)(10()()(2+++=*s s s z s K s G 产生纯虚根为1j ±的z 值和*K 值；（2）概略绘出)23)(23)(5.3)(1()(j s j s s s s Ks G -+++++=*的闭环根轨迹图（要求确定根轨迹的渐近线、分离点、与虚轴交点和起始角）。

4-７ 已知控制系统的开环传递函数为 22)94(2)()(+++=*s s s K s H s G ）（试概略绘制系统根轨迹。

4-８ 已知系统的开环传递函数为)93()(2++=*s s s Ks G试用根轨迹法确定使闭环系统稳定的K 值范围。

自动控制_根轨迹(例题)

自动控制_根轨迹(例题)

n
m
n
m
nm

j 1
i 1
nm
这是与实轴交点为－，斜率为 tg

(2k 1) nm
是渐近线方程。渐近线与实轴的夹角(称为渐近线的倾斜角为
k 0,1,2
( 2k 1) 的直线方程。也就 nm
180



0
n m 1
nm 2
90 0

和
实轴上的会合点和分离点的求法
由此得： D( d ) K gd N ( d ) 0 ' ' D ( ) K N ( d ) 0 d gd 即：
N ' ( s ) D( s ) N ( s ) D ' ( s ) 0 D( s ) K gd N ( s) s d
二．根据相角条件确定根轨迹上的点
设某一系统的开环零极点如图，在Ｓ 平面中的任意一点 S0 ，用相角条件可
s0
O
× p2
以判断 S0 是不是根轨迹的点。
1、从 S0 到各零极点连直线
2、用量角器量 (s0 p1 )，…等各个角 3、将量好的值代入（＊＊）式，若等
式成立，则 S0 就是根轨迹上的点
j 1 i 1 i
当 Kg= 0 时，有 s = pj ( j =1, 2, … , n) 上式说明Kg= 0时，闭环特征方程的根就是开环极点。
将特征方程改写为：
1 Kg
(s p ) (s z ) 0
j 1 j i 1 i
n
m
当 Kg 时，有
s = zi
( i =1, 2, … , m)
z1
o

《自动控制原理》第4章_根轨迹分析法

《自动控制原理》第4章_根轨迹分析法
一般有两个解，从中
因此求分离点和会合点公式： 可以判断是分离点或
N(s)D '(s) N '(s)D(s) 0 会合点，只有满足条
Kg 0
件Kg≥0的是有用解。
例4-1.设系统结构如图， 试绘制其概略根轨迹。
R(s)
k(s 1) c(s)
s(s 2)(s 3)
解：画出 s 平面上的开环零点（-1），开环极点（0， -2，-3）。
逆时针为正。（- ， ）
m
n
pj (2k 1) ( z j pi ) pj pi
j 1
j 1
ji
m
n
zi (2k 1) ( z j zi ) p j zi
j 1
j 1
j i
k 0,1,
k 0, 1,
例3.设系统开环传递函数为： G(s) Kg(s 1.5)(s 2 j)(s 2 j) s(s 2.5)(s 0.5 j1.5)(s 0.5 j1.5)
K
s1
00
0.5 1
1 1 j1
s2
K
K 2.5
2
K 1
1 K 0
1 j1
2 1
2 1 j 3 1 j 3
1 j 1 j
j
2
1
0
K 0.5
1
2
一、根轨迹的一般概念
开环系统（传递函数）的某一个参数从零变化到 无穷大时，闭环系统特征方程根在 s 平面上的轨迹 称为根轨迹。
根轨迹法:图解法求根轨迹。 借助开环传递函数来求闭环系统根轨迹。
nm
独立的渐近线只有（n-m）条 u=0,1…,(n-m-1)
（2）渐近线与实轴的交点
分子除以分母

自动控制原理-第四章-根轨迹法16

自动控制原理-第四章-根轨迹法16

§4.3
广义根轨迹
§4.3.1 参数根轨迹 — 除 K* 之外其他参数变化时系统的根轨迹
例2
系统开环传递函数
G(s)
(s a) 4，a=0→∞
s2 (s 1)
变化，绘制根轨迹；x1时，
F(s)?
解. (1) D(s) s3 s2 1 s 1 a 0
4
构造 “ 等效开环传递函数 ”
4 G*(s)
开环稳定 ≠ 闭环稳定
负反馈未必一定能改善系统性能
§4.4
绘制根轨迹的基本法则（20）
例3 单位反馈系统的开环传递函数为 G(s) K *(Ts 1) ，选定K*值，绘制
当T变化时的根轨迹。
s(s 1)( s 2)
D(s) s(s 1)( s 2) K *(Ts 1) 0
G*(s)
90
④ 与虚轴交点：7D(s) 4s3 s2 (14K 10)s 7(K 1) 0
ReD( j) 2 7(K 1) 0 ImD( j) 4 3 (14 10) 0
0
K 1
2
K9 7
§4.2
绘制根轨迹的基本法则（19）
例1 系统结构图如图所示
（1）绘制当K*= 0→∞ 时系统的根轨迹； （2）分析系统稳定性随K*变化的规律。 解. (2) 分析：
j)]
3
(2
20T
)
0
2.582
T 0.233
K * 20 K* 6 K* 3
自动控制原理
（第 16 讲）
§4 根轨迹法
§4.1 根轨迹法的基本概念 §4.2 绘制根轨迹的基本法则 §4.3 广义根轨迹 §4.4 利用根轨迹分析系统性能
自动控制原理
（第 16 讲）

自动控制原理-题库-第四章-线性系统根轨迹-习题

自动控制原理-题库-第四章-线性系统根轨迹-习题

4-1将下述特征方程化为适合于用根轨迹法进行分析的形式，写出等价的系统开环传递函数。

（1）210s cs c +++=，以c 为可变参数。

（2）3(1)(1)0s A Ts +++=，分别以A 和T 为可变参数。

（3）1()01I D P k k s k G s ss τ⎡⎤+++=⎢⎥+⎣⎦，分别以P k 、I K 、T 和τ为可变参数。

4-2设单位反馈控制系统的开环传递函数为(31)()(21)K s G s s s +=+试用解析法绘出开环增益K 从0→+∞变化时的闭环根轨迹图。

4-2已知开环零极点分布如下图所示，试概略绘出相应的闭环根轨迹图。

4-3设单位反馈控制系统的开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求确定分离点坐标）。

（1）()(0.21)(0.51)KG s s s s =++（2）(1)()(21)K s G s s s +=+（3）(5)()(2)(3)K s G s s s s +=++4-4已知单位反馈控制系统的开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求算出起始角）。

（1）(2)()(12)(12)K s G s s s j s j +=+++-（2）(20)()(1010)(1010)K s G s s s j s j +=+++-4-5设单位反馈控制系统开环传递函数如为*2()()(10)(20)K s z G s s s s +=++试确定闭环产生纯虚根1j ±的z 值和*K 值。

4-6已知系统的开环传递函数为*22(2)()()(49)K s G s H s s s +=++试概略绘出闭环根轨迹图。

4-7设反馈控制系统中*2()(2)(5)KG s s s s =++（1）设()1H s =，概略绘出系统根轨迹图，判断闭环系统的稳定性（2）设()12H s s =+，试判断()H s 改变后的系统稳定性，研究由于()H s 改变所产生的影响。

机电控制工程基础习题课课后习题答案 第四章习题

机电控制工程基础习题课课后习题答案 第四章习题

1)
0.4(s 1)(s 5) s3 9s2 26s 18
习题 3 已知单位负反馈系统的开环传递函数为
0.25(s a) G(s) s2 (s 1)
a的变化范围为(0, ) ，试绘制系统的闭环根轨迹。
解：系统闭环特征方程为 D(s) s3 s2 0.25s 0.25a
即有
1
s3
0.25a s2 0.25s
分离角2k1pill为根轨迹分支数10525比较12知系统1不稳定2稳定且系统性能由一对共轭复极点主导极点决定随着k值增大第三个极点逐渐靠近零点成为偶极子系统性能仍由这对共轭复极点决定练习的根皆为实数试确定参数的范围
习题４－ 2 (2) G(s)H (s) K (0.4s 1) K *(s 2.5)
s(0.2s 1) s(s 5)
i
(3) G(s)H (s) K (0.5s 1)(0.25s 1) K (s 2)(s 4)
(s 1)(0.125s 1) (s 1)(s 8)
i
习题４－3 已知单位负反馈系统开环传递函数为 G(s)
K
s(s 1)(0.5s 1)
，试作出Ｋ从 0 变化的闭环根轨迹（按步骤做，写明
60
,180
, 120
（4）根轨迹的分离点。
由分离点方程
d
K *(3s2 2s 0.25)
dx G1(s)
s2 (s 0.5)
0
解得：
d1
1 2
, d2
1 6
（5）根轨迹与虚轴的交点。
根据闭环特征方程写劳斯表如下
s3
1
0.25
s2
1
0.25a
s1
0.25-0.25a
当a=1时，劳斯表的 s1 行元素全为零，辅助方程为

根轨迹法习题及答案

根轨迹法习题及答案

第四章 根轨迹法习题及答案4-1 系统的开环传递函数为)4s )(2s )(1s (K )s (H )s (G *+++=试证明3j 1s 1+-=在根轨迹上，并求出相应的根轨迹增益*K 和开环增益K 。

解 若点1s 在根轨迹上，则点1s 应满足相角条件π)12()()(+±=∠k s H s G ，如图所示。

对于31j s +-=，由相角条件=∠)s (H )s (G 11-++-∠-)13j 1(0=++-∠-++-∠)43j 1()23j 1(ππππ-=---632满足相角条件，因此311j s +-=在根轨迹上。

将1s 代入幅值条件：143j 123j 113j 1K s H )s (G *11=++-⋅++-⋅++-=）（解出 ： 12K *= ， 238K K *==4-2 已知单位反馈系统的开环传递函数如下，试求参数b 从零变化到无穷大时的根轨迹方程，并写出2b =时系统的闭环传递函数。

（1）)b s )(4s (02)s (G ++=（2）)b s )(2s (s )b 2s (01)s (G +++=解 (1) )4j 2s )(4j 2s ()4s (b 20s 4s )4s (b )s (G 2-++++=+++=' 28s 6s 20)s (G 1)s (G )s (2++=+=Φ(2) )10s 2s (s )20s 2s (b )s (G 22++++='=)3j 1s )(3j 1s (s )19j 1s )(19j 1s (b -+++-+++ 40s 14s 4s )4s (10)s (G 1)s (G )s (23++++=+=Φ 4-3 已知单位反馈系统的开环传递函数)b s )(4s (s2)s (G ++=，试绘制参数b 从零变化到无穷大时的根轨迹，并写出s=-2这一点对应的闭环传递函数。

解 )6s (s )4s (b )s (G ++='根轨迹如图。

第四章习题答案

第四章习题答案

解：系统结构图为：
R(S) G(S) C(S)
特征方程为：1 + G ( S ) = 0
S 3 + 2S 2 + S + S + a = 0 S + 2S + 2S + a = 0
3 2
S +a 1+ =0 2 S ( S + 1)
a 整理： 1 + 3 =0 2 S + 2S + 2S
∴ 等效开环传递函数为：
∴闭环特征方程为：S 3 + 6S 2 + 9S + a = 0
a 1+ 3 =0 整理得： 2 S + 6S + 9S
（根轨迹方程）
令
a a G(S ) = 3 = 2 S + 6 S + 9 S S ( S + 3) 2
为等效的开环传递函数
根轨迹方程：G ( S ) = −1 当 a 从0 → ∞ 时，开环零点： m = 0 ，开环极点：
( S + 2)( S + 1) ( S + 2)( S + 1) S ( S + 1) = φ (S ) = ( S + 2)( S + 1) S ( S + 1) + ( S + 2)( S + 1) 1+ S ( S + 1) ( S + 2)( S + 1) ( S + 2)( S + 1) = = 2( S + 1)( S + 1) 2( S + 1) 2
d1 = −2 + 3
d 2 = −2 − 3 舍掉，不在根轨迹上

自动控制原理 第四章 线性系统的根轨迹方法(2011-3) (2)

自动控制原理 第四章 线性系统的根轨迹方法(2011-3) (2)
要求等价为：
பைடு நூலகம்β = 45
−ξπ 1−ξ 2
β = 60
[ s]
j
⎧45° < β < 60° ⎨ ⎩ 2 < ωn < 5
−5
−2
0
13
ξ ξ ξ ξ ξ ξ ξ
= 0.0 σ % = 100% = 0.4 σ % = 25% = 0.5 σ % = 15% = 0.6 σ % = 10% = 0.7 σ % = 5% = 0.8 σ % = 2% = 1.0 σ % = 0%
A
ξ = 0.5
Im
λ3 = −2.34 X
−2
λ1 = −0.33 + j0.58
−1
X
−0.5
60
0
X
Re
λ2 = −0.33 − j0.58
21
三、高阶系统动态性能指标估算
1、高阶系统单位阶跃响应
(1) 高阶系统的单位阶跃响应包括常数项和响应模态。 (2) 除常数项以外，高阶系统的单位阶跃响应是系统模态的组 合，组合系数即部分分式系数。 (3) 模态由闭环极点确定，而部分分式系数与闭环零点、极点 分布有关，闭环零点、极点对系统动态性能均有影响。
ξ ≥ 1− r
( α)
2
ωd ≤ r
α − r ≤ ωn ≤ α + r
α − r ≤ ξωn ≤ α + r
如果设定区域
ξωn ≥ q
则选择 r ≤ min
(α − q , α
ξ ≥ ξ min
1− ξ
2 min
)
8
[例]：如图系统，求系统具有最小阻尼时K值及相应的 动态性能和稳态误差。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章 根轨迹法
4-1试粗略画出对应反馈控制系统具有以下前向和反馈传递函数的根轨迹图： ()()()
()s s H s s s K s G 6.01,01.01.02
+=++=
4-2 试粗略地画出反馈系统函数 ()()()()
2
411+-+=
s s s K
s G 的根轨迹。

4-3 对应负反馈控制系统，其前向和反馈传递函数为 ()()()
()1,42)
1(2
=+++=
s H s s s s K s G 试粗略地画出系统的根轨迹。

4-4 对应正反馈重做习题4-3，试问从你的结果中得出什么结论？
4-5 试画出具有以下前向和反馈传递函数的，正反馈系统根轨迹的粗略图。

()()()()1,412
2=++=
s H s s K
s G
4-6 试确定反馈系统开环传递函数为 ()()()()()
5
284)
2(2
+++++=
s s s s s s K s H s G 对应-∞<K<∞的根轨迹。

指明所有根轨迹上的相应特征。

4-7 设一负反馈系统，其开环传递函数 ()()()()()
90020040)4(2
++++=
s s s s s K s H s G a) 画出根轨迹并表明根轨迹上全部特征值。

b) 增益值在一个什么样的范围内，系统才是稳定的？ c) 画出系统的伯德图，并使其稳定性和不稳定性区域，与根轨迹图连系起来说明。

4-8 对应负反馈情况，重做习题4-7.
4-9 对应如下的负反馈控制系统，粗略地作出根轨迹，并确定系统稳定下K 的范围。

()()()
()1,41)
6(=+++=
s H s s s s K s G
4-10 对应习题4-10图所示系统，根据以下条件，试确定导致系统稳定的正实数增益K 的范围：
a) 具有负反馈的系统。

b) 具有正反馈的系统。

习题4-10图
4-11 已知反馈系统的开环传递函数
*
()()(1)(2)
K G s H s s s s =
++ 试绘制系统的根轨迹图，详细列写根轨迹的计算过程，其中包括零点、极点、渐近线及与实轴交点，根轨迹分离点及与虚轴的交点、渐近线与实轴夹角。

求出根轨迹及与虚轴相交时的K *
及相应的开环增益K 。

4-12 已知负反馈系统的闭环特征方程
K 1+(s+14)(s 2
+2s+2)=0
(1) 绘制系的根轨迹图（0<K1<∞）；
(2) 确定使复数闭环主导极点的阻尼系数ζ=0.5的K 1值。

4-13 已知某单位反馈系统的开环传递函数
*2
()(1)
K G s s s =+
试绘制系统的根轨迹图，说明其稳定性。

如果负实轴上增加一个零点-a(0≤a ≤1)，对系统的稳定性有何影响，仍以根轨迹图来说明。

4-14 已知某单位反馈系统的闭环根轨迹图如习题4-14图所示
（1）确定使系统稳定的根轨迹增益K *
的范围； （2）写出系统临界阻尼时的闭环传递函数。

习题4-14图
4-15已知某单位反馈系统的开环传递函数
*(1)()(2)(3)
K s G s s s s +=
++
试绘制闭环系统的概略根轨迹。

4-16已知反馈系统的开环传递函数
*
2
()()(4)(420)
K G s H s s s s s =+++ 试绘制闭环系统的概略根轨迹。

4-17如果某单位反馈系统的开环传递函数为
*()1
K G s s =
+
试用解析法绘制K *
从零到无穷时的闭环系统的根轨迹图，并判断下列点是否在根轨迹上：
（-2+j0），（0+j1），（-3+j2）
4-18 设某单位反馈系统的开环传递函数为
*
()(0.011)(0.021)
K G s s s s =
++ (1) 绘制闭环系统的根轨迹；
(2)确定使系统临界稳定的开环增益K C ；
(3)确定使系统临界阻尼比相应的开环增益K C 。

4-19非最小相位系统的特征方程为
(s+1)(s+3)(s-1)(s-3)+K *(S 2
+4)=0
试绘制该系统的根轨迹图。

4-20已知反馈系统的开环传递函数
(0.251)()()(0.51)
K s G s H s s s +=
+ 试用根轨迹法确定系统无超调响应时的开环增益K 。

4-21 如习题4-21图所示控制系统： (1)绘制该系统的根轨迹图；
(2)求系统输出c(t)无振荡分量时的闭环传递函数。

习题4-21图
4-22 设负反馈系统的开环传递函数为
*
()()(3)(2)
K G s H s s s =
++ 试绘制闭环系统的概略根轨迹。

若系统： （1） 增加一个z=-5的零点； （2） 增加一个z=-2.5的零点； （3） 增加一个z=-0.5的零点。

试绘制增加零点后系统的根轨迹，并分析增加零点后根轨迹的变化规律和对系统性能的影响。

4-23 设负反馈系统的开环传递函数为
2
() , ()(1)
K
G s H s s a s s =
=++ （1） 利用MATLAB 有关函数作出0≤a<1时系统的根轨迹和单位阶跃响应曲线； （2） 讨论a 值变化对系统动态性能及稳定性的影响（0≤a<1）。