5常用概率分布3

概率论与数理统计公式整理在现代数学中，概率论与数理统计是两个重要的分支。

其中概率论是研究随机事件发生的可能性或概率的科学。

而数理统计则是利用概率论的方法，对已经发生的随机事件进行统计分析和推断。

本文将整理概率论与数理统计中常用的公式。

一、基本概率公式1.概率：$P(A)=\frac{n(A)}{n(S)}$其中，$P(A)$表示事件$A$发生的概率，$n(A)$表示事件$A$所包含的基本事件的个数，$n(S)$表示所有基本事件的个数。

2.加法原理：$P(A\cup B)=P(A)+P(B)-P(A\cap B)$其中，$A$和$B$是两个事件，$A\cup B$表示事件$A$和事件$B$中至少有一个发生的概率，$A\cap B$表示两个事件同时发生的概率。

3.条件概率：$P(B|A)=\frac{P(A\cap B)}{P(A)}$其中，$P(B|A)$表示在事件$A$发生的条件下，事件$B$发生的概率。

4.乘法定理：$P(A\cap B)=P(A)P(B|A)$其中，$P(A\cap B)$表示两个事件同时发生的概率，$P(B|A)$表示在事件$A$发生的条件下，事件$B$发生的概率。

二、概率分布1.离散随机变量的概率分布律：$\sum\limits_{i=1}^{+\infty}{p(x_i)}=1$其中，$p(x_i)$表示离散随机变量取值为$x_i$的概率。

2.连续随机变量的概率密度函数：$\int_{-\infty}^{+\infty}{f(x)}\mathrm{d}x=1$其中，$f(x)$表示连续随机变量在$x$处的概率密度。

3.数学期望：$E(x)=\sum\limits_{i=1}^{+\infty}{x_ip(x_i)}$或$E(x)=\int_{-\infty}^{+\infty}{xf(x)}\mathrm{d}x$其中，$E(x)$表示随机变量$x$的数学期望，$p(x_i)$表示$x_i$这一离散随机变量取到的带权概率。

目录1. 均匀分布 (1)2. 正态分布（高斯分布） (2)3. 指数分布 (2)4. Beta分布（：分布） (2)5. Gamm 分布 (3)6. 倒Gamm分布 (4)7. 威布尔分布（Weibull分布、韦伯分布、韦布尔分布） (5)8. Pareto 分布 (6)9. Cauchy分布（柯西分布、柯西-洛伦兹分布） (7)210. 分布（卡方分布） (7)8 11. t分布................................................9 12. F分布 ...............................................10 13. 二项分布............................................10 14. 泊松分布（Poisson 分布）.............................11 15. 对数正态分布........................................1. 均匀分布均匀分布X ~U（a,b）是无信息的，可作为无信息变量的先验分布。

2. 正态分布（高斯分布）当影响一个变量的因素众多，且影响微弱、都不占据主导地位时，这个变量 很可能服从正态分布，记作X~N （」f 2）。

正态分布为方差已知的正态分布N （*2）的参数」的共轭先验分布。

1 空f （x ）： —— e 2-J2 兀 o'E(X)， Var(X) _ c 23. 指数分布指数分布X ~Exp （ ）是指要等到一个随机事件发生，需要经历多久时间。

其 中，.0为尺度参数。

指数分布的无记忆性：Plx s t|X = P{X t}。

f （X ）二 y oiE(X) 一4. Beta 分布（一：分布）f （X ）二 E(X)Var(X)=(b-a)2 12Var(X)二1~2Beta 分布记为X 〜Be(a,b)，其中Beta(1,1)等于均匀分布，其概率密度函数 可凸也可凹。

第七章概率统计方法概率分布及数字特征；样本与统计量；参数估计法；案例分析：足球门的危险区域问题；案例分析：最优评卷问题。

1.一维随机变量与分布函数一.概率分布与数字特征随机变量：用数值表示的随机事件的函数。

分布函数：设ξ为一随机变量，对任意的实数x 有函数)()()(x P x P x F ≤=≤<-∞=ξξ称为随机变量ξ的分布函数。

对任意两个实数)(,2121x x x x <，则有)()()(1221x F x F x x P -=≤<ξ如果随机变量ξ所有取值有限个或可列无穷个数值，则这种随机变量为离散型随机变量。

非离散型的随机变量，则称为连续型的随机变量。

如果ξ为离散型随机变量，所有的取值为 ,2,1,=k x k ，则称 ,2,1,)(===k p x P k k ξ为随机变量ξ的分布列，其相应的分布函数为∑≤=x x k k px F )(。

如果ξ为连续型随机变量，则分布函数定义为 ⎰∞-=xdx x f x F )()(,其中)(x f 为一个非负可积函数，称之为随机变量ξ的分布密度，或密度函数。

具有下列性质： （1）0)(≥x f ； （2）1)(=⎰+∞∞-dx x f ；（3）dx x f a F b F b a P ba ⎰=-=≤<)()()()(ξ；（4）当)(x f 为连续函数时有)()(x f x F ='。

（1）数学期望设ξ为离散型随机变量，其分布列为 ,2,1,)(===k p x P k k ξ，如果级数∑∞=1k k k p x收敛，则称∑∞=1k k k p x 为随机变量ξ的数学期望，记为ξE ，即∑∞==1k k k p xE ξ。

2. 随机变量的数学期望与方差一.概率分布与数字特征设ξ为连续型随机变量，其分布密度函数为 )(x f ，如果dx x f x ⎰+∞∞-)(收敛，则称dx x xf ⎰+∞∞-)(为随机变量ξ的数学期望，记为ξE ，即dx x xf E ⎰+∞∞-=)(ξ。

目录1. 均匀分布 ...................................................................................................... 1 2. 正态分布（高斯分布） ........................................................................... 2 3. 指数分布 ...................................................................................................... 2 4. Beta 分布（β分布） ............................................................................. 2 5. Gamma 分布 .................................................................................................. 3 6. 倒Gamma 分布 ............................................................................................. 4 7. 威布尔分布(Weibull 分布、韦伯分布、韦布尔分布) ................. 5 8. Pareto 分布 ................................................................................................ 6 9. Cauchy 分布（柯西分布、柯西-洛伦兹分布） . (7)10. 2χ分布（卡方分布） (7)11. t 分布 ........................................................................................................ 8 12. F 分布 ........................................................................................................ 9 13. 二项分布 ................................................................................................ 10 14. 泊松分布（Poisson 分布） ............................................................. 10 15.对数正态分布 .......................................................................................111. 均匀分布均匀分布~(,)X U a b 是无信息的，可作为无信息变量的先验分布。

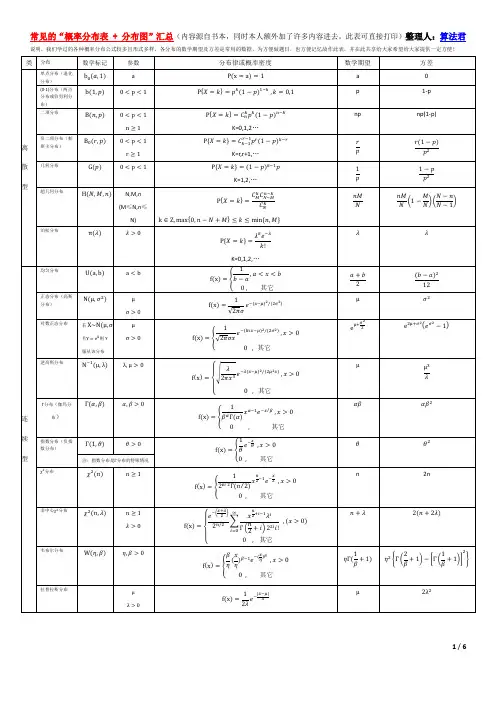
简单样本的概率分布在统计学中，概率分布是描述随机变量取值概率的数学表达方式。

对于简单样本的概率分布，我们通常指的是连续型随机变量的概率分布，如正态分布、泊松分布等。

这些分布形式在各种应用场景中都有广泛的应用，例如金融、生物、医学等领域。

一、简单样本的概率分布概念简单样本的概率分布是指从一个总体中随机抽取若干个样本，每个样本具有相同的概率分布形式。

通常，我们抽取的样本数量越多，样本的概率分布就越接近总体概率分布。

因此，简单样本的概率分布可以用来估计总体的概率分布。

二、常见的简单样本概率分布1.正态分布正态分布是最常见的连续型概率分布之一，其概率密度函数呈钟形曲线。

正态分布在自然界和人类社会中广泛存在，如人类的身高、考试分数等都呈现出正态分布的特点。

正态分布的数学表达式为：f(x)=1σ2πe−(x−μ)22σ2f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(x)=2πσ21e−2σ2(x−μ)2其中，μ是均值，σ是标准差。

2.泊松分布泊松分布是一种离散型概率分布，常用于描述单位时间内随机事件发生的次数。

泊松分布在物理学、生物学、经济学等领域都有应用。

泊松分布的数学表达式为：P(X=k)=λke−λP(X=k) = \frac{\lambda^k}{k!} e^{-\lambda}P(X=k)=k!λke −λ其中，λ是泊松分布的参数，表示单位时间内随机事件发生的平均次数。

3.二项分布二项分布是一种离散型概率分布，常用于描述随机试验中成功的次数。

例如，抛硬币试验、扔骰子等都可以用二项分布来描述。

二项分布的数学表达式为：P(X=k)=Cnkpk(1−p)n−kP(X=k) = C_n^k p^k (1-p)^{n-k}P(X=k)=knpk(1−p)n−k 其中，CnkC_n^kCnk表示组合数，即从 n 个不同元素中取出 k 个元素的组合方式数；p 是每次试验成功的概率；n 是试验次数。

常见的概率分布离散分布0-1分布(伯努利分布)它的分布律为：\[P\{X=k\}=p^k(1-p)^{1-k}, k=0,1, (0<p<1)\]0-1分布记作：\(X \sim b(1,p)\)期望：\(E(X)=p\)⽅差:\(D(X)=p(1-p)\)常⽤的场景：新⽣婴⼉性别的登记，招⽣考试的录取，产品的是否合格，硬币的正反⾯。

⼆项分布⼆项分布为\(n\)重伯努利实验的概率分布。

分布律为：\[P\{X=k\}=\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k},k=0,1,2,...,n,(0<p<1)\]\[\sum\limits_{k=0}^{n}P\{X=k\}=\sum\limits_{k=0}^{n}\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}=(p+1-p)^n=1\]⼆项分布记作：\( X \sim b(n,p)\)期望：\(E(X)=np\)⽅差:\(D(X)=np(1-p)\)常⽤的场景：⽐如⼀个⼈射击\(n\)次，其中\(k\)次命中的概率，抽查50台设备，其中10台出故障的概率等等。

从下⾯的图中，我们可以看到命中次数先增加，到了3达到最⼤，之后⼜逐渐减少，⼀般来说，对于固定的\(n,p\)，都具有这⼀性质。

（1）当\(（n+1）p\)不为整数时，⼆项概率\(P\{X=k\}\)在\(k=[(n+1)p]\)时达到最⼤值；（2）当\(（n+1）p\)为整数时，⼆项概率\(P\{X=k\}\)在\(k=(n+1)p,k=(n+1)p-1\)时达到最⼤值。

%每轮射击10次，命中概率0.3，射击10000轮，x中返回的是每轮中命中的次数x=binornd(10,0.3,10000,1);%bin的数⽬为10hist(x,10);N=100;p=0.4;k=0:N;%事件发⽣k次的概率pdf=binopdf(k,N,p);%事件发⽣不⼤于k次的概率cdf=binocdf(k,N,p);plotyy(k,pdf,k,cdf);grid on;多项分布多项式分布是⼆项式分布的扩展，在多项式分布所代表的实验中，⼀次实验会有多个互斥结果，⽽⼆项式分布所代表的实验中，⼀次实验只有两个互斥结果。