空间解析几何-第5章 正交变换与仿射变换

空间解析几何的正交变换正交变换的性质与计算正交变换是一类在空间解析几何中具有重要地位的变换。

它是指在空间中既保持长度不变，又保持两向量之间的夹角不变的变换。

在此文章中，我们将探讨正交变换的性质与计算方法。

一、正交变换的定义与性质正交变换在空间解析几何中被广泛运用。

它是指一个线性变换，使得空间中的任意向量经过该变换后，向量的长度保持不变，并且向量之间的夹角也保持不变。

具体而言，设给定空间中的两个向量A和B，经过正交变换T后，它们的长度和夹角分别为A'和B'。

则有以下性质：1. 长度不变：经过正交变换T后，向量的长度保持不变，即|A|=|A'|，|B|=|B'|。

2. 夹角不变：经过正交变换T后，向量之间的夹角保持不变，即∠(A,B)=∠(A',B')。

3. 内积不变：经过正交变换T后，向量之间的内积保持不变，即A·B=A'·B'。

4. 正交性：若经过正交变换T后的向量A'与向量B'垂直（即A'⊥B'），则原始向量A与B也一定垂直（即A⊥B）。

二、正交变换的计算方法根据上述性质，我们可以利用矩阵来计算正交变换。

设空间中的向量A=[a₁, a₂, a₃]，我们可以构造一个正交矩阵T，满足以下性质：1. T的行、列是正交单位向量2. T的行、列是长度为1的向量有了正交矩阵T，我们可以通过矩阵乘法来计算变换后的向量A'：A' = T·A计算变换后的向量B'时，同样可以使用上述公式。

对于特定的正交变换，我们可以使用不同的矩阵来进行计算。

例如：1. 旋转变换：设给定一个旋转轴n和一个旋转角度θ，对于任意向量n，它的旋转变换可以表示为：R(θ) = [cosθ+nₓ²(1-cosθ), nₓnᵧ(1-cosθ)-n n sinθ, nₓn_z(1-cosθ)+n_ssinθ][nₓnᵧ(1-cosθ)+n_sn_z, nᵧ²(1-cosθ)+n n sinθ, nᵧn_z(1-cosθ)-n_ssinθ][nₓn_z(1-cosθ)-n_ssinθ, nᵧn_z(1-cosθ)+n_ssinθ, n_z²(1-cosθ)+nnsinθ]其中n = [nₓ, nᵧ, n_z]为旋转轴的单位向量，θ为旋转角度。

空间几何的仿射变换几何学是研究图形、空间、数量等概念的学科。

其中，空间几何是研究空间运动和空间图形之间的关系的学科。

空间几何中有一个重要的概念叫做仿射变换，它在空间几何中有着广泛的应用，尤其是在计算机图形学和计算机视觉中。

一、什么是仿射变换先来看下什么是仿射变换。

简单地说，仿射变换是保持点之间的“比例关系”的变换，它是一种线性变换和平移变换的组合。

在二维平面中，一个仿射变换可以用一个$3\times3$的矩阵表示如下：$$\begin{bmatrix}s_{x}&r_{x}&t_{x}\\r_{y}&s_{y}&t_{y}\\0&0 &1\end{bmatrix}$$其中，$s_{x}$和$s_{y}$表示水平方向和垂直方向的缩放因子，$r_{x}$和$r_{y}$表示水平方向和垂直方向的倾斜，$t_{x}$和$t_{y}$表示水平方向和垂直方向的平移。

在三维空间中，一个仿射变换可以用一个$4\times4$的矩阵表示如下：$$\begin{bmatrix}s_{x}&r_{x}&p_{x}&t_{x}\\r_{y}&s_{y}&p_ {y}&t_{y}\\r_{z}&p_{z}&s_{z}&t_{z}\\0&0&0&1\end{bmatrix}$$其中，$s_{x}$、$s_{y}$和$s_{z}$表示三个方向的缩放因子，$r_{x}$、$r_{y}$和$r_{z}$表示绕三个坐标轴的旋转角度，$p_{x}$、$p_{y}$和$p_{z}$表示绕三个坐标轴的旋转中的剪切因子，$t_{x}$、$t_{y}$和$t_{z}$表示三个方向的平移量。

二、仿射变换的应用1. 计算机图形学在计算机图形学中，仿射变换可以用来实现图形的旋转、缩放、平移、剪切等操作。

比如，平移可以通过使用平移矩阵来实现：$$\begin{bmatrix}1&0&t_{x}\\0&1&t_{y}\\0&0&1\end{bmatrix} $$缩放可以通过使用缩放矩阵来实现：$$\begin{bmatrix}s_{x}&0&0\\0&s_{y}&0\\0&0&1\end{bmatrix} $$旋转可以通过使用旋转矩阵来实现：$$\begin{bmatrix}\cos\theta&-\sin\theta&0\\\sin\theta&\cos\theta&0\\0&0&1\end{bmatrix}$$等等。

解析几何中的仿射与相似变换解析几何是数学中一个重要的分支，研究的是平面和空间中的几何图形，其中涉及到各种各样的变换。

在解析几何中，仿射变换和相似变换是两个常见的变换类型，它们在几何图形的研究和应用中发挥着重要的作用。

一、仿射变换仿射变换是指保持直线平行性和直线上的点的比例关系的变换。

形式上，对于平面上的点P(x, y)，经过仿射变换得到的新点P'(x', y')满足以下关系：x' = a1x + a2y + a3y' = b1x + b2y + b3其中a1、a2、a3、b1、b2、b3是常数，且a1b2 - a2b1 ≠ 0。

对于仿射变换，我们可以将其分解成平移、旋转、缩放和剪切四个基本变换的组合。

具体而言：1. 平移变换：平移变换将点P(x, y)移动到新的位置P'(x', y')，其中新位置与原位置的坐标之差为一个常量向量(v1, v2)。

对于平面上的点P(x, y)，经过平移变换得到的新点P'(x', y')满足以下关系：x' = x + v1y' = y + v22. 旋转变换：旋转变换将点P(x, y)绕一个固定的点O(x0, y0)逆时针旋转θ弧度。

对于平面上的点P(x, y)，经过旋转变换得到的新点P'(x', y')满足以下关系：x' = (x - x0)cosθ - (y - y0)sinθ + x0y' = (x - x0)sinθ + (y - y0)cosθ + y03. 缩放变换：缩放变换将点P(x, y)绕一个固定的点O(x0, y0)按照比例因子k进行缩放。

对于平面上的点P(x, y)，经过缩放变换得到的新点P'(x', y')满足以下关系：x' = k(x - x0) + x0y' = k(y - y0) + y04. 剪切变换：剪切变换通过把点P(x, y)沿着某个方向按照比例因子k进行剪切。

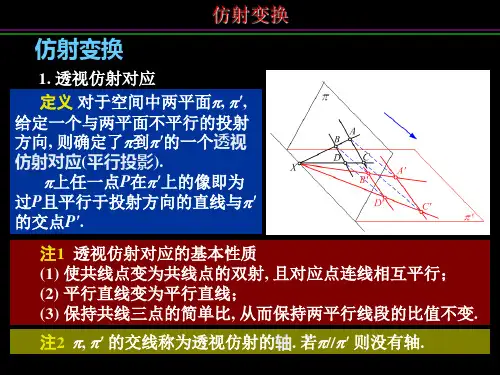
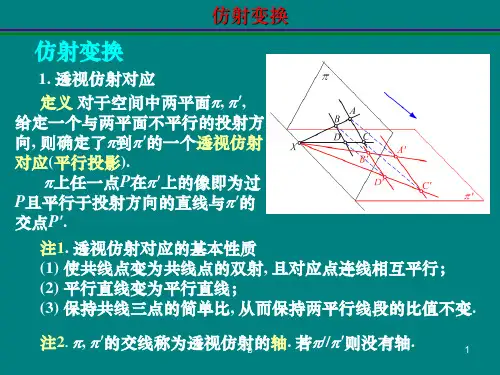
解析几何是数学中的一个分支，研究了几何图形在坐标系中的表示和性质。

而仿射变换是解析几何中的一个重要概念，它描述了几何图形在平移、旋转、缩放等变换下的性质和关系。

仿射变换是指在二维或三维空间中，通过平移、旋转、缩放、错切等操作，将一个几何图形映射到另一个几何图形的变换。

它保持了几何图形的平行性、共线性和比例性质，因此在很多几何问题的研究和应用中具有重要作用。

在二维空间中，仿射变换可以用矩阵表示。

设原始图形的坐标为(x, y)，经过仿射变换后的坐标为(x', y')，则可以表示为如下的矩阵形式：```[x'] [a b] [x] [e][y'] = [c d] * [y] + [f][1 ] [0 0] [1] [1]```其中，矩阵的左上角2x2部分表示旋转、缩放、错切等线性变换；右侧的列向量表示平移变换。

仿射变换具有许多重要的性质和应用。

首先，仿射变换可以保持几何图形的形状、大小和相对位置关系。

例如，通过平移可以将一个图形移动到另一个位置，通过旋转可以改变图形的朝向，通过缩放可以调整图形的大小。

其次，仿射变换可以用来解决许多几何问题。

例如，通过仿射变换可以计算两个几何图形之间的距离、角度、相交关系等。

它也可以用来生成各种特殊形状的图形，如椭圆、双曲线等。

此外，仿射变换还在计算机图形学、计算机视觉等领域中得到广泛应用。

通过仿射变换，可以实现图像的旋转、平移、缩放等操作，从而实现图像的处理和变换。

在计算机视觉中，仿射变换可以用来进行图像的校正、配准等操作。

总之，仿射变换是解析几何中的一个重要概念，它描述了几何图形在平移、旋转、缩放等变换下的性质和关系。

通过仿射变换，我们可以研究和解决许多几何问题，实现图形的处理和变换。

在实际应用中，仿射变换在计算机图形学、计算机视觉等领域中具有广泛的应用价值。

目录中文题目 (1)中文摘要关键词 (1)英文摘要关键词 (1)引言 (2)一、正交变换 (2)（一）正交变换的定义 (2)（二）正交变换在数学中的应用 (3)二、仿射变换 (10)（一）仿射变换的定义及其性质 (10)（二）仿射变换在数学中的应用 (11)三、射影变换 (14)（一）射影变换的定义 (14)（二）射影变换在数学中的应用 (16)四、近似变换 (19)（一）近似变换的定义 (19)（二）近似变换在数学中的应用 (20)结束语 (22)参考文献 (22)数学中的变换————几种常见变换在数学中的应用王鸾凤（渤海大学数学系 辽宁 锦州 121000 中国）摘要：数学中的数学变换有很多种，本文对几种常见的数学变换——正交变换、仿射变换、射影变换、相似变换的定义及其在数学中的应用做了总结。

正交变换是欧氏空间中的一类重要的变换，是保持向量内积不变的变换，正因为它有这一特征，使正交变换在高等代数中起着重要的作用。

不仅如此，正交变换在多元函数积分中、多元Tarlor 公式中也有独到的应用。

仿射变换是几何中的一个重要变换，它是从运动变换到射影变换的桥梁。

灵活的运用仿射变换，能使一些初等几何问题由繁到简。

射影变换中二维射影变换定理及其应用非常重要。

相似变换可以把求一个较复杂的函数()F x 迭代根转化为求一个较简单的函数()G x 迭代根的问题。

关键词：正交变换，仿射变换，射影变换，相似变换。

Transformation in mathematics----------------Several common transformations in the application of mathematicsWang Luanfeng(Department of Mathematics Bohai University Liaoning Jinzhou 121000 China)Abstract: There are many mathematical transformations in mathematics. In this paper, it summarizes the definition of the orthogonal transformation, affine representation, projective transformation and similar transformation. It also summarizes the application of problem-solving in mathematics. Orthogonal transformation is a major transformation in Euclidean space ，it maintains the measure of the transformation. Precisely because of this character, orthogonal transformation plays an important role in advanced algebra. Moreover, orthogonal transformation also has unique applications in the integration of multi-function, multi-formula, and so on. Affine transformation plays an important role in geometry, it is the transition from the movement to transform projective transform. Flexible usage of affine transformation makes some complex elementary geometry problems simple. The tow-dimensional projection transform theorem and its application is very important in the projective transformation. Similar transformation can make a complex problem of Gen-function iteration become simpler.Keywords: Orthogonal transformation ，Affine representation ，Projective transformation ， Similar transformation.引言我们在大学中学习了许多数学变换，接触了数学中的正交变换、仿射变换、射影变换、相似变换等，它们在数学中的应用非常广泛，正交变换在数学分析、高等几何、高等代数等学科中的解题有着很重要的应用，仿射变换、射影变换在高等几何中的图形变换的解题非常重要，相似变换在高等代数中的多项式解题有着非常灵活的应用，下面就这些数学变换的应用做出总结。

空间中的几何变换与仿射变换空间中的几何变换与仿射变换是几何学中重要的概念，它们描述了物体在空间中的平移、旋转、缩放和扭曲等变化。

本文将对这两种变换进行介绍，并探讨它们在计算机图形学和计算机视觉中的应用。

一、几何变换几何变换是指物体在空间中的位置和形状发生变化的操作。

常见的几何变换包括平移、旋转和缩放。

这些变换可以通过矩阵运算来表示。

1. 平移变换平移变换是物体在空间中沿着某一方向移动一定的距离。

它可以用一个平移向量来描述，即将物体的每个点坐标都加上平移向量的分量。

设物体上的一个点P坐标为 (x, y, z)，平移变换的平移向量为(dx, dy, dz)，则物体经过平移变换后的坐标为 (x+dx, y+dy, z+dz)。

2. 旋转变换旋转变换是物体围绕某一中心点旋转一定的角度。

它可以用旋转矩阵来表示，旋转矩阵的元素根据旋转轴和旋转角度的不同而有所变化。

对于二维空间，以原点为中心，逆时针旋转角度θ的旋转变换可以表示为以下矩阵形式：| cosθ -sinθ || si nθ cosθ |对于三维空间，旋转变换涉及到欧拉角和四元数等复杂的数学概念，这里不做详细讨论。

3. 缩放变换缩放变换是物体的每个点坐标根据缩放因子进行放大或缩小的操作。

它可以用一个缩放矩阵来表示。

设物体上的一个点P坐标为 (x, y, z)，缩放变换的缩放因子为(sx, sy, sz)，则物体经过缩放变换后的坐标为 (sx * x, sy * y, sz * z)。

二、仿射变换仿射变换是一种保持了直线、平行线和比例关系的变换。

它是几何变换的一种扩展，包含了平移、旋转、缩放和剪切等操作。

仿射变换可以用一个仿射矩阵来表示，仿射矩阵对应了一个线性变换和一个平移变换。

线性变换可以用矩阵乘法表示，而平移变换可以用平移向量加法表示。

1. 线性变换线性变换是指一个向量在空间中经过旋转和缩放等变换后的结果。

它可以用一个线性变换矩阵来表示。

设物体上的一个点P的坐标为 (x, y, z)，线性变换矩阵为 A，则物体经过线性变换后的坐标为 A * P。

仿射变换方程怎么解以仿射变换方程怎么解引言：仿射变换是一种常见的几何变换方法，可以用于对图像进行旋转、平移、缩放和错切等操作。

本文将介绍仿射变换方程的解法，帮助读者更好地理解和应用仿射变换。

一、什么是仿射变换？仿射变换是指在平面上对点进行旋转、平移、缩放和错切等操作的变换方式。

它可以通过一个线性变换和一个平移向量来表示。

具体而言，对于平面上的点 (x, y)，经过仿射变换后的点 (x', y') 可以通过以下公式计算得出：x′=xx+xx+xx′=xx+xx+x其中，a、b、c、d、e 和 f 是仿射变换的参数。

二、仿射变换方程的解法1.已知三对点坐标的情况下当给定三对点的坐标时，我们可以利用这些已知点来求解仿射变换方程的参数。

假设已知的点分别为 (x1, y1) -> (x1', y1')，(x2, y2) -> (x2', y2') 和 (x3, y3) -> (x3', y3')，则可以得到以下三个方程：x1′=xx1+xx1+xx1′=xx1+xx1+xx2′=xx2+xx2+xx2′=xx2+xx2+xx3′=xx3+xx3+xx3′=xx3+xx3+x通过解这个方程组，我们可以求解出a、b、c、d、e 和f 的值，从而得到仿射变换的参数。

2.已知变换矩阵的情况下除了通过已知点来求解仿射变换方程的参数，我们还可以通过已知变换矩阵的方式来解方程。

假设已知的变换矩阵为 M，即[x′1 x′1] = [x1 x1 1] x其中，[x′1 x′1] 是经过仿射变换后的点的坐标，[x1 x1 1] 是原始点的齐次坐标。

则根据仿射变换的定义，可以得到以下方程：x′1=x1x+x1x+xx′1=x1x+x1x+x通过解这个方程组，我们可以求解出仿射变换的参数。

三、应用实例仿射变换在计算机图形学和计算机视觉领域有着广泛的应用。

仿射变换理论及其在几何中的应用仿射变换理论在儿何中地位非常重要，它比正交变换解决的问题范围更广.本文中我们将看到仿射坐标系，在仿射坐标系中我们了解仿射变换和仿射变换的基本性质，例如包括仿射变换将直线变为直线，将平行的两条直线变为半行的两直线。

本文中还介绍单比，利用它证明了梅内劳斯(Menelaus)定理。

后來本文介绍了仿射不变性质，例如两个三角形面积的比是仿射不变量。

最后本文介绍了利用本文的有关性质解决一些问题。

这样使得读者更好的了解这篇文章。

欧式儿何就是研究正交变换下图形的不变性质与不变量，因此在初等平面儿何中都是讨论图形的那些与距离，角度,面积，等有关的性质，如三角形全等，平行，垂直等•但是图形的各种变形中，保持任意两点之间的距离不变的变换是十分特殊.例如，图形的放大，物体在阳光照射下变成它们的影子等，都不具有这种性质，即都不是正交变换•因此，我们考虑较正交变换广泛一点的点变换，即仿射变换.本文讨论了仿射变换的槪念及其性质，同时给出了其在儿何中的应用.1平面上的仿射坐标系与仿射变换我们引进仿射坐标系：在半面上任取一点。

及两个不共线的向量5 二O 瓦,=OE2(不一定是单位向量，EG,.不一定垂直的)这样我们就建立了仿射坐标系如图1对于平面上任一点尸，则向量。

户可唯一地表示为OP = xei + yei数组&y)称为关于仿射坐标系仁由,/},的仿射坐标.定理1. 0在仿射坐标系下，直线方程一定是关于仿射坐标系的一次方程Ax+By+C = 0,(1. 00)反之也真.证明在直线上任取两点小演，乂)，2(9,%),对于直线上任一点P幺有联II鹤，即&-演K-K'或(工一占)(治一必)一(丁一九)(毛一%)二。

，这是关于X,y的一次方程.反之，在(1.00)±取£ (公弘)及《(毛用)的坐标适合方程，即Ar. + B\,+C = 0, (1. 02)A V3 + By： + C = 0. (1. 03)只要证明任一坐标适合方程的点P' 3, y') 一定与共线即可，由TAx + By + C = Q, (1. 04)因A, B,C不全为零,(1.02), (1.03), (1.04)可理解为关于A, 5, C ,的齐次线性方程组，由于A,民。

空间直角坐标转换之仿射变换一、仿射变换仿射变换是空间直角坐标变换的一种，它是一种二维坐标到二维坐标之间的线性变换，保持二维图形的“平直线”和“平行性”，其可以通过一系列的原子变换的复合来实现，包括平移(Translation)、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切(Shear)。

此类变换可以用一个3×3的矩阵来表示，其最后一行为(0, 0, 1)。

该变换矩阵将原坐标(x, y)变换为新坐标(x', y')，这里原坐标和新坐标皆视为最末一行为(1)的三维列向量，原列向量左乘变换矩阵得到新的列向量：[x'] [m00 m01 m02] [x] [m00*x+m01*y+m02][y'] = [m10 m11 m12] [y] = [m10*x+m11*y+m12][1 ] [ 0 0 1 ] [1] [ 1 ]如果将它写成按旋转、缩放、平移三个分量的复合形式，则其代数式如下：x’= m00*x+m01*y+m02；y’= m10*x+m11*y+m12；其示意图如下：几种典型的仿射变换：1.public static AffineTransform getTranslateInstance(double tx, double ty)平移变换，将每一点移动到(x+tx, y+ty)，变换矩阵为：[ 1 0 tx ][ 0 1 ty ][ 0 0 1 ]（译注：平移变换是一种“刚体变换”，rigid-body transformation，中学学过的物理，都知道啥叫“刚体”吧，就是不会产生形变的理想物体，平移当然不会改变二维图形的形状。

同理，下面的“旋转变换”也是刚体变换，而“缩放”、“错切”都是会改变图形形状的。

）2.public static AffineTransform getScaleInstance(double sx, double sy)缩放变换，将每一点的横坐标放大（缩小）至sx倍，纵坐标放大（缩小）至sy倍，变换矩阵为：[ sx 0 0 ][ 0 sy 0 ][ 0 0 1 ]3.public static AffineTransform getShearInstance(double shx, double shy)剪切变换，变换矩阵为：[ 1 shx 0 ][ shy 1 0 ][ 0 0 1 ]相当于一个横向剪切与一个纵向剪切的复合[ 1 0 0 ][ 1 shx 0 ][ shy 1 0 ][ 0 1 0 ][ 0 0 1 ][ 0 0 1 ]（译注：“剪切变换”又称“错切变换”，指的是类似于四边形不稳定性那种性质，街边小商店那种铁拉门都见过吧？想象一下上面铁条构成的菱形拉动的过程，那就是“错切”的过程。