菱形知识要点归纳

菱形【要点梳理】要点一、菱形的定义有一组邻边相等的平行四边形叫做菱形.要点诠释：菱形的定义的两个要素：①是平行四边形.②有一组邻边相等.即菱形是一个平行四边形，然后增加一对邻边相等这个特殊条件.要点二、菱形的性质菱形除了具有平行四边形的一切性质外，还有一些特殊性质：1.菱形的四条边都相等；2.菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.3.菱形也是轴对称图形，有两条对称轴（对角线所在的直线），对称轴的交点就是对称中心.要点诠释：（1）菱形是特殊的平行四边形，是中心对称图形，过中心的任意直线可将菱形分成完全全等的两部分.（2）菱形的面积由两种计算方法：一种是平行四边形的面积公式：底×高；另一种是两条对角线乘积的一半（即四个小直角三角形面积之和）.实际上，任何一个对角线互相垂直的四边形的面积都是两条对角线乘积的一半.（3）菱形可以用来证明线段相等，角相等，直线平行，垂直及有关计算问题.要点三、菱形的判定菱形的判定方法有三种：1.定义：有一组邻边相等的平行四边形是菱形.2.对角线互相垂直的平行四边形是菱形.3.四条边相等的四边形是菱形.要点诠释：前两种方法都是在平行四边形的基础上外加一个条件来判定菱形，后一种方法是在四边形的基础上加上四条边相等.【典型例题】类型一、菱形的性质1、如图所示，菱形ABCD中，E、F分别是BC、CD上的点，∠B＝∠EAF＝60°，∠BAE ＝18°．求∠CEF的度数．【思路点拨】由已知∠B＝60°，∠BAE＝18°，则∠AEC＝78°．欲求∠CEF的度数，只要求出∠AEF的度数即可，由∠EAF＝60°，结合已知条件易证△AEF为等边三角形，从而∠AEF＝60°．【答案与解析】解：连接AC．∵四边形ABCD是菱形，∴ AB＝BC，∠ACB＝∠ACF．又∵∠B＝60°，∴△ABC是等边三角形．∴∠BAC＝∠ACB＝60°，AB＝AC．∴∠ACF＝∠B＝60°．又∵∠EAF＝∠BAC＝60°∴∠BAE＝∠CAF．∴△ABE≌△ACF．∴ AE＝AF．∴△AEF为等边三角形．∴∠AEF＝60°．又∵∠AEF＋∠CEF＝∠B＋∠BAE，∠BAE＝18°，∴∠CEF＝18°．【总结升华】当菱形有一个内角为60°时，连接菱形较短的对角线得到两个等边三角形，有助于求相关角的度数．在求角的度数时，一定要注意已知角与所求角之间的联系．2、已知：如图所示，四边形ABCD是菱形，过AB的中点E作AC的垂线EF，交AD于点M，交CD的延长线于点F．(1)求证：AM＝DM；(2)若DF＝2，求菱形ABCD的周长．【答案与解析】证明：(1)连接DB，则由菱形性质得BD⊥AC．又因为EF⊥AC，所以EF∥BD，即ME∥BD．又因为点E是AB的中点，所以点M是AD的中点．所以AM＝DM．(2)由(1)得DB∥EF．又BE∥DF，所以四边形EFDB是平行四边形．所以BE＝DF＝2．又因为12BE AB，即AB＝2BE＝2×2＝4．所以菱形ABCD的周长为4×4＝16．【总结升华】菱形四边相等，对角线互相垂直平分.举一反三：【变式】（2015春•潍坊期中）如图，在菱形ABCD中，对角线AC、BD相交于点O，E是AB的中点，如果EO=2，求四边形ABCD的周长．解：∵四边形ABCD为菱形，∴BO=DO，即O为BD的中点，又∵E是AB的中点，∴EO是△ABD的中位线，∴AD=2EO=2×2=4，∴菱形ABCD的周长=4AD=4×4=16．类型二、菱形的判定3、（2014春•郑州校级月考）如图，在等边三角形ABC中，BC=6cm，射线AG∥BC，点E从点A出发沿射线AG以lcm/s的速度运动，同时点F从点B出发沿线射BC以2cm/s 的速度运动，设运动时间为t（s）．（1）连接EF，当EF经过AC边的中点D时，求证：△ADE≌△CDF；（2）当t为多少时，四边形ACFE是菱形．【思路点拨】（1）由题意得到AD=CD，再由AG与BC平行，利用两直线平行内错角相等得到两对角相等，利用AAS即可得证；（2）若四边形ACFE是菱形，则有CF=AC=AE=6，由E的速度求出E运动的时间即可．【答案与解析】（1）证明：∵AG∥BC，∴∠EAD=∠DCF，∠AED=∠DFC，∵D为AC的中点，∴AD=CD，在△ADE和△CDF中，，∴△ADE≌△CDF（AAS）；（2）解：①若四边形ACFE是菱形，则有CF=AC=AE=6，则此时的时间t=6÷1=6（s）．故答案为：6s．【总结升华】此题考查了菱形的判定，全等三角形的判定与性质等知识，弄清题意是解本题的关键.【变式】已知，在△ABC中，AB＝AC＝a，M为底边BC上任意一点，过点M分别作AB、AC 的平行线交AC于P，交AB于Q.⑴求四边形AQMP的周长；⑵M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由.【答案】解：（1）∵MQ∥AP，MP∥AQ，∴四边形AQMP是平行四边形∴QM＝AP又∵AB＝AC，MP∥AQ，∴∠2＝∠C，△PMC是等腰三角形，PM＝PC∴QM＋PM＝AP＋PC＝AC＝a∴四边形AQMP的周长为2a（2）M位于BC的中点时，四边形AQMP为菱形.∵M位于BC的中点时,易证△QBM与△PCM全等,∴QM＝PM,∴四边形AQMP为菱形类型三、菱形的综合应用4、如图所示，菱形ABCD中，AB＝4，∠ABC＝60°，∠EAF＝60°，∠EAF的两边分别交BC、CD于E、F．(1)当点E、F分别在边BC、CD上时，求CE＋CF的值．(2)当点E、F分别在CB、DC的延长线时，CE、CF又存在怎样的关系，并证明你的结论．【思路点拨】(1)由菱形的性质可知AB＝BC，而∠ABC＝60°，即联想到△ABC为等边三角形，∠BAC＝60°，又∠EAF＝60°，所以∠BAE＝∠CAF，可证△BAE≌△CAF，得到BE＝CF，所以CE+CF＝BC．(2)思路基本与(1)相同但结果有些变化．【答案与解析】解：(1)连接AC．在菱形ABCD中，BC＝AB＝4，AB∥CD．∵∠ABC＝60°，∴ AB＝AC＝BC，∠BAC＝∠ACB＝60°．∴∠ACF＝60°，即∠ACF＝∠B．∵∠EAF＝60°，∠BAC＝60°，∴∠BAE＝∠CAF．∴△ABE≌△ACF(ASA)，∴ BE＝CF．∴ CE＋CF＝CE＋BE＝BC＝4．(2)CE－CF＝4．连接AC如图所示．∵∠BAC＝∠EAF＝60°，∴∠EAB＝∠FAC．∵∠ABC＝∠ACD＝60°，∴∠ABE＝∠ACF＝120°．∵ AB＝AC，∴△ABE≌△ACF(ASA)，∴ BE＝CF．∴ CE－CF＝CE－BE＝BC＝4．【总结升华】(1)菱形的性质的主要应用是证明角相等、线段相等、两直线平行、两线段互相垂直、互相平分等．(2)注意菱形中的60°角的特殊性，它让菱形这个特殊的平行四边形变得更加特殊，常与等边三角形发生联系．。

数学菱形知识点总结一、菱形的定义菱形是一个四边形，它有着以下几个特点：1. 四边相等：菱形的四条边长度相等。

2. 对角线相等：菱形的两条对角线长度相等。

3. 相邻角相等：菱形的相邻两个角是相等的，并且相邻角的和是180度。

二、菱形的性质菱形是一种特殊的平行四边形，在平行四边形的基础上，菱形还有以下几个特殊的性质：1. 对角线垂直：菱形的对角线互相垂直。

2. 对角平分：菱形的对角线互相平分对角。

3. 对角线平分：菱形的对角线互相平分四边形的面积。

4. 对角线角度：菱形的对角线夹角为90度。

三、菱形的面积菱形的面积可以通过以下公式计算：菱形的面积=对角线1乘以对角线2除以2即S=d1*d2/2其中，d1和d2分别是菱形的两条对角线的长度。

通过这个公式，我们可以很容易地计算菱形的面积。

四、菱形的周长菱形的周长可以通过以下公式计算：菱形的周长=4乘以边长即P=4L其中，L是菱形的边长。

通过这个公式，我们可以很容易地计算菱形的周长。

五、菱形的性质应用菱形的性质在实际问题中有着广泛的应用，包括以下几个方面：1. 计算几何中的面积：当我们知道了菱形的对角线长度时，可以利用菱形的面积公式计算菱形的面积，从而解决相关问题。

2. 计算几何中的周长：当我们知道了菱形的边长时，可以利用菱形的周长公式计算菱形的周长，从而解决相关问题。

3. 利用菱形的垂直性求解问题：利用菱形对角线的垂直性质，可以解决一些与菱形相关的几何问题。

六、总结菱形是数学中一个重要的几何图形，它具有独特的性质和广泛的应用。

通过本文的介绍，读者可以更加全面地理解和掌握菱形的相关知识，从而更好地解决与菱形相关的数学问题。

希望本文对读者有所帮助，谢谢！。

第一章特殊的平行四边形一、菱形：【知识梳理】1．菱形的定义：有一组邻边相等的平行四边形叫做菱形．2．菱形的性质菱形是特殊的平行四边形，它具有平行四边形的所有性质，•还具有自己独特的性质：①边的性质：对边平行且四边相等．②角的性质：邻角互补，对角相等．③对角线性质：对角线互相垂直平分且每条对角线平分一组对角．④对称性：菱形是中心对称图形，也是轴对称图形．菱形的面积等于底乘以高，等于对角线乘积的一半．点评：其实只要四边形的对角线互相垂直，其面积就等于对角线乘积的一半．3．菱形的判定判定①：一组邻边相等的平行四边形是菱形．判定②：对角线互相垂直的平行四边形是菱形．判定③：四边相等的四边形是菱形．【例题精讲】板块一、菱形的性质例1.如图，菱形ABCD的对角线交于点O，AC=16cm，BD=12cm．（1）求菱形ABCD的边长；（2）求菱形ABCD的高DM．例2.如图，在菱形ABCD中，AB=BD，点E，F分别在AB，AD上，且AE=DF．连接BF与DE相交于点G，连接CG与BD相交于点H．求证：（1）求∠BGD的度数。

（2）求证：DG+BG=CG例3.将两张宽度相等的长方形纸片叠放在一起得到如图29所示的四边形ABCD .(1)求证：四边形ABCD 是菱形．(2)如果两张长方形纸片的长都是8，宽都是2，那么菱形ABCD 的周长是否存在最大值或最小值？如果存在，请求出来；如果不存在，请简要说明理由．例4.已知，菱形ABCD 中，E 、F 分别是BC 、CD 上的点，若AE AF EF AB ===，求C ∠的度数．FEDCBA跟踪练习：1.如图,在菱形ABCD 中,AB=5,对角线AC=6.若过点A 作AE ⊥BC,垂足为E,则AE 的长为( )A.4B.2.4C.4.8D.52.如图，在菱形ABCD 中，∠B=60°，AB=2，E 、F 分别是BC 和CD 的中点，连接AE 、EF 、AF ，则△AEF 的周长为（ ）A.23B.33C.43D.3.3.如图所示,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()A.15°或30°B.30°或45°C.45°或60°D.30°或60°4．如图1－1－38，在给定的一张平行四边形纸片ABCD上作一个菱形，甲、乙两人的作法如下：图1－1－38甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于点M，O，N，连接AN，CM，则四边形ANCM是菱形．乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于点E，F，连接EF，则四边形ABEF是菱形．根据两人的作法可判断()A．甲正确，乙错误B．甲错误，乙正确C．甲、乙均正确D．甲、乙均错误5. (1) 如图所示,在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4 cm.那么,菱形ABCD 的面积是________,对角线BD的长是________.(2) 如图：菱形ABCD中，AB=2，∠B=120°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是_________．6.如图，在四边形ABCD中，E为AB上一点，△ADE和△BCE都是等边三角形，AB、 BC、CD、DA的中点分别为P、Q、M、N，试判断四边形PQMN为怎样的四边形，并证明你的结论．7.如图所示，在菱形ABCD中，∠ABC=60°，DE∥AC交BC的延长线于点E．求证：DE=BE．8.如图，在菱形ABCD中，∠A=60°，AB=4，O为对角线BD的中点，过O点作OE⊥AB，垂足为E．（1）求∠ABD的度数；（2）求线段BE的长．9.如图，四边形ABCD是菱形，BE⊥AD、BF⊥CD，垂足分别为E、F．（1）求证：BE=BF；（2）当菱形ABCD的对角线AC=8，BD=6时，求BE的长．10.如图，在菱形ABCD中，P是AB上的一个动点（不与A、B重合），连接DP交对角线AC于E连接BE．（1）证明：∠APD=∠CBE；（2）若∠DAB=60°，试问P点运动到什么位置时，△ADP的面积等于菱形ABCD面积的，为什么？11.如图所示，在矩形ABCD中，AB=4cm，BC=8cm、点P从点D出发向点A运动，同时点Q从点B出发向点C运动，点P、Q的速度都是1cm/s．（1）在运动过程中，四边形AQCP可能是菱形吗？如果可能，那么经过多少秒后，四边形AQCP是菱形？（2）分别求出菱形AQCP的周长、面积．【作业】一. 选择题：1..在菱形ABCD中，AB=5cm，则此菱形的周长为（）A. 5cmB. 15cmC. 20cmD. 25cm2.如图，在菱形ABCD中，∠BAD=60°，BD=4，则菱形ABCD的周长是____3.已知菱形ABCD的对角线AC、BD的长度是6和8，则这个菱形的周长是（）A、20B、14C、28D、244.如图，菱形ABCD的周长是16，∠A=60°，则对角线BD的长度为（）A．2 B．23 C．4 D．435.已知菱形ABCD中，对角线AC与BD交于点O，∠BAD=120°，AC=4，则该菱形的面积是（ ） A 、16错误!未找到引用源。

菱形面积的知识点总结一、菱形的定义菱形是一种特殊的四边形，其四条边相等，对角线相等且互相垂直。

菱形的性质独特，其面积的计算也有其特殊的方法。

在日常生活中，我们可以看到许多物体的形状类似菱形，了解菱形的性质和计算方法对我们理解这些事物和进行实际计算有一定的帮助。

二、菱形的面积计算菱形的面积计算可以通过两种方法进行，一种是利用菱形的对角线长度来计算，另一种是利用菱形的内切圆的半径来计算。

1. 利用对角线计算菱形的面积设菱形的对角线长度分别为d1和d2，则菱形的面积S可由下式计算得出：S = (d1 * d2) / 2其中，d1和d2分别为菱形的两条对角线长度。

2. 利用内切圆半径计算菱形的面积设菱形的内切圆的半径为r，则菱形的面积S可由下述公式计算得出：S = 4 * (r * r)其中，r为菱形的内切圆的半径。

在实际计算中，我们可以根据菱形的已知条件，选择合适的计算方法，来求解菱形的面积。

三、菱形的性质除了面积的计算，菱形还具有一些重要的性质，这些性质在物理、数学等领域都有一定的应用价值。

1. 对角线互相垂直菱形的两条对角线互相垂直，也就是说，对角线的交点处的角度为90度，这个性质在物理学上具有一定的应用价值，对于一些倾斜的结构体或者机械构件的设计和分析有一定的帮助。

2. 对角线长度相等菱形的两条对角线长度相等，这一特性也体现了菱形的对称性，对于图形的构造和分析有一定的帮助。

3. 内切圆菱形可以内切一个圆，这个圆的半径就是菱形的内切圆的半径，菱形的内切圆和菱形本身具有一定的对称性，而内切圆半径也可以用来计算菱形的面积。

四、菱形的应用菱形的性质和面积计算方法在日常生活和工作中都有一定的应用。

1. 建筑设计在建筑设计中，有很多建筑结构的形状类似菱形，比如钢筋混凝土的楼梯结构、玻璃幕墙的构造等，了解菱形的性质和计算方法可以帮助设计师更好地理解和设计这些建筑结构。

2. 机械设计在机械设计制造领域，有很多机械构件的形状也类似菱形，比如传送带的支撑结构、轴承的支撑结构等，了解菱形的性质和计算方法可以帮助工程师更好地设计和分析这些机械构件。

有关菱形知识点总结一、菱形的定义菱形是一种具有四个边长相等的四边形，同时具有两条对角线互相垂直且等长的特殊几何形状。

菱形的定义可以用几何学的术语表示为：一个具有四个相等边长的四边形，并且具有两条互相垂直且等长的对角线的图形即为菱形。

二、菱形的性质1. 对角线相等菱形的两条对角线互相垂直且等长。

这是菱形独特的性质之一，也是区分菱形与其他四边形的重要特征。

可以通过勾股定理来证明菱形的对角线相等。

2. 对角线平分菱形的两条对角线分别将菱形对角的角度平分。

这个性质可以很容易地通过菱形的几何构图来呈现。

3. 对边相等菱形的四条边互相等长，即具有相等的边长。

这是菱形的基本特征之一，也是菱形与其他四边形的区别之一。

4. 内角性质菱形内角之间的夹角和为360度。

这个性质可以通过菱形的内角和为360度来证明。

5. 对角度性质菱形的内角均为直角，且每个内角大小为90度。

6. 对顶点性质菱形的每个顶点均为菱形的对角线的交点，即对角线的中点。

7. 对角线角度菱形的对角线之间的夹角为90度。

这个性质是由于菱形的对角线互相垂直而得出的。

三、菱形的公式1. 面积公式菱形的面积公式为：S= d1*d2/2，其中S为菱形的面积，d1和d2分别表示菱形的两条对角线的长度。

2. 周长公式菱形的周长公式为：P= 4a，其中P为菱形的周长，a表示菱形的一个边长。

四、菱形的应用菱形作为一种特殊的四边形，在几何学中具有很多应用，常见的有以下几个方面：1. 建筑设计在建筑设计中，菱形的几何形状常常被运用到建筑物的外观设计中。

例如，一些现代建筑的外墙设计就会采用菱形的图案来增加建筑的美观性和独特性。

2. 画框设计在画框设计中，菱形的形状常常被用作画框的设计图案。

例如，一些艺术品的画框就会采用菱形的形状来突出画作的艺术感。

3. 几何学教学在几何学教学中，菱形作为一种特殊的四边形，经常被用来进行几何学知识的教学。

通过菱形的性质和公式等知识点的学习，可以帮助学生更好地理解和掌握几何学的知识。

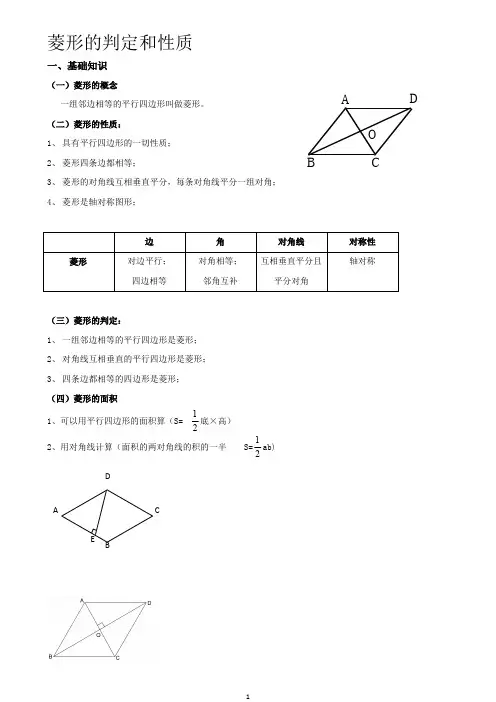
BCADO菱形的判定和性质一、基础知识（一）菱形的概念一组邻边相等的平行四边形叫做菱形。

（二）菱形的性质：1、 具有平行四边形的一切性质；2、 菱形四条边都相等；3、 菱形的对角线互相垂直平分，每条对角线平分一组对角；4、 菱形是轴对称图形；边 角 对角线 对称性 菱形对边平行； 四边相等对角相等； 邻角互补互相垂直平分且平分对角轴对称（三）菱形的判定：1、 一组邻边相等的平行四边形是菱形；2、 对角线互相垂直的平行四边形是菱形；3、 四条边都相等的四边形是菱形； （四）菱形的面积1、可以用平行四边形的面积算（S=21底×高） 2、用对角线计算（面积的两对角线的积的一半 S=21ab)ABCDE二、例题讲解考点一 ：菱形的判定例1：下列命题正确的是（ ）（A ） 一组对边相等，另一组对边平行的四边形一定是平行四边形 （B ） 对角线相等的四边形一定是矩形 （C ） 两条对角线互相垂直的四边形一定是菱形（D ） 两条对角线相等且互相垂直平分的四边形一定是正方形 练习1：菱形的对角线具有( ) A ．互相平分且不垂直 B ．互相平分且相等 C ．互相平分且垂直 D ．互相平分、垂直且相等练习2：如图，菱形ABCD 中，对角线AC 、BD 相交于点O ，M 、N 分别是边AB 、AD 的中点，连接OM 、ON 、MN ，则下列叙述正确的是（ ） A ．△AOM 和△AON 都是等边三角形B ．四边形AMON 与四边形ABCD 是位似图形C ．四边形MBON 和四边形MODN 都是菱形D ．四边形MBCO 和四边形NDCO 都是等腰梯形练习3：如图，在三角形ABC 中，AB ＞AC ，D 、E 分别是AB 、AC 上的点，△ADE 沿线段DE 翻折，使点A 落在边BC 上，记为A '．若四边形ADA E '是菱形，则下列说法正确的是( )A ．DE 是△ABC 的中位线B ．AA '是BC 边上的中线 C ．AA '是BC 边上的高D ．AA '是△ABC 的角平分线ABCDEA 'DBCA NM O练习4：如图，下列条件之一能使平行四边形ABCD 是菱形的为（ ） ①AC BD ⊥ ②90BAD ∠= ③AB BC = ④AC BD = A ．①③B ．②③C ．③④D ．①②③例2 ：已知AD 是△ABC 的平分线，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ，则四边形AEDF 是什么四边形？请说明理由．变化：若D 是等腰三角形底边BC 的中点，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ，则四边形AEDF 是什么四边形？请说明理由．练习1：如图，AD 是Rt △ABC 斜边上的高，BE 平分∠B 交AD 于G ，交AC 于E ，过E 作EF ⊥BC 于F ，试说明四边形AEFG 是菱形．练习2：如图，E 是菱形ABCD 边AD 的中点，EF ⊥AC 于点H ，交CB 延长线于点F ，交AB 于点G ，求证：AB 与EF 互相平分。

菱形知识点全总结1. 菱形是一个四边形，有四条边，每两条边长度相等，且相邻的两条边夹角是直角。

2. 菱形也可以被看作是一个平行四边形，因为它有两组对边互相平行。

二、菱形的性质1. 对角线的性质a. 菱形的对角线互相垂直且相等长。

b. 对角线互相平分对角。

2. 边的性质a. 菱形的四条边长度相等。

b. 相邻边夹角是直角。

c. 相对边互相平行。

3. 角的性质a. 菱形的每个内角是直角。

b. 菱形的四个角相等。

4. 对角线与边的关系a. 对角线、边和角的关系可以应用正弦、余弦和正切的关系式来计算。

三、菱形的相关公式1. 菱形的周长公式周长 = 4 × 边长2. 菱形的面积公式面积 = 对角线1 × 对角线2 ÷ 2四、菱形的应用1. 几何图形的构建菱形是一种常见的几何图形，可以作为其他几何图形的组成部分。

2. 建筑设计在建筑设计中，菱形常用于窗户、天花板和地板的设计。

3. 工程测量在工程测量中，菱形可以用于测量与角度有关的工程数据。

4. 人造物体许多人造物体，如菱形图案的地砖、墙壁等，都设计成菱形的形状。

五、菱形的属性1. 对角线的垂直性对角线互相垂直是菱形的重要属性，可以用于解决与菱形相关的几何问题。

2. 对角线的长度确定对角线的长度可以帮助我们计算菱形的面积和周长。

3. 菱形的边长知道菱形的边长可以帮助我们确定其它属性，如周长和面积。

六、菱形的相关定理1. 菱形的内角和是360°因为菱形是一个四边形，所以它的内角和等于360°。

2. 菱形的每个角都是90°证明：根据菱形的定义和角的性质，可以得出菱形的每个角都是90°。

3. 菱形的属性定理根据对角线的垂直性和长度、边长的关系，可以得出一些菱形的属性定理，用于解决相关的几何问题。

七、菱形的相关图形1. 平行四边形菱形可以被看作是一个特殊的平行四边形，因为它有两组对边互相平行，同时也有其他平行四边形的性质。

(完整版)第十八章菱形知识点总结
1. 菱形定义和特性
菱形是一种几何形状，具有以下特性：
- 拥有四条边和四个角，其中每个角都是直角。

- 两条对角线相等且垂直交叉。

- 对角线的交点称为菱形的中心。

2. 菱形的性质
- 对角线相等性质：菱形的两条对角线相等。

- 对角线垂直性质：菱形的两条对角线相互垂直。

- 边长平行性质：菱形的相邻边互相平行。

3. 菱形的周长和面积计算公式
- 周长计算公式：菱形的周长等于边长乘以4，即 `周长 = 4 ×边长`。

- 面积计算公式：菱形的面积等于对角线之积的一半，即 `面积= (对角线1 ×对角线2) / 2`。

4. 菱形的相关图形和实际应用
- 平行四边形：菱形的特殊情况，具有相邻边平行的性质。

- 菱形切割：通过两个垂直相交的菱形切割，可以得到多个边长相等的小菱形。

- 菱形形状的物体：例如球场的中央足球场草坪通常呈现菱形形状。

5. 菱形的重要性和研究价值
- 菱形是几何学中重要的基本形状之一，了解和掌握菱形的定义和性质对进一步研究和理解其他几何形状非常有帮助。

- 菱形相关的计算公式可以应用于解决实际生活中的问题，例如计算球场草坪的总面积等。

- 掌握菱形的切割方法和相关技巧，能够发展和培养几何思维和想象力。

6. 总结
第十八章菱形知识点总结了菱形的定义、特性、性质、周长和面积计算公式，以及菱形的相关图形和实际应用。

菱形作为几何学中的重要形状，掌握其知识和技巧对学习和应用几何学具有重要意义。

希望这份总结能够帮助你更好地理解和掌握菱形的相关知识。

数学知识点总结之菱形
数学知识点总结之菱形
菱形是特殊的平行四边形之一。

有一组邻边相等的平行四边形称为菱形。

下面是小编为大家收集的数学知识点总结之菱形，希望能够帮助到大家。

菱形：
①一组邻边相等的平行四边形是菱形。

②领心的四条边相等，两条对角线互相垂直平分，每一组对角线平分一组对角。

③判定条件：定义/对角线互相垂直的平行四边形/四条边都相等的四边形。

以上就是对菱形知识点的总结学习，相信同学们已经很好的记住了，上面的知识一定对同学们的学习有很好的帮助。

拓展：
平面直角坐标系：
在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系。

水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴，两坐标轴的交点为平面直角坐标系的.原点。

平面直角坐标系的要素：
①在同一平面；
②两条数轴；
③互相垂直；
④原点重合。

三个规定：
①正方向的规定横轴取向右为正方向，纵轴取向上为正方向。

②单位长度的规定；一般情况，横轴、纵轴单位长度相同；实际有时也可不同，但同一数轴上必须相同。

③象限的规定：右上为第一象限、左上为第二象限、左下为第三
象限、右下为第四象限。

相信上面对平面直角坐标系知识的讲解学习，同学们已经能很好的掌握了吧，希望同学们都能考试成功。

菱形的断定及知识点归纳
菱形的断定
① 四条边都相等的四边形是菱形。

② 对角线互相垂直且平分的平行四边形是菱形。

③ 一组邻边相等的平行四边形是菱形。

④对角线平分一组对角的平行四边形是菱形。

菱形知识点归纳
1、菱形的定义 :有一组邻边相等的平行四边形叫做菱形。

2、菱形的性质:⑴ 矩形具有平行四边形的一切性质;
⑵ 菱形的四条边都相等;
⑶ 菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。

⑷ 菱形是轴对称图形。

提示:利用菱形的性质可证得线段相等、角相等，它的对角线互相垂直且把菱形分成四个全等的直角三角形，由此又可与勾股定理联络，
可得对角线与边之间的关系，即边长的平方等于对角线一半的平方和。

3、菱形的断定方法:
⑴ 定义:一组邻边相等的平行四边形是菱形。

⑵ 判断方法1:对角线互相垂直的平行四边形是菱形。

⑶ 判断方法2:四条边相等的四边形是菱形。

4、菱形面积的计算:
菱形面积 = 底×高 = 对角线长乘积的一半 S菱形
=1/2×ab(a、b为两条对角线)
归纳:对角线互相垂直的四边形的面积等于对角线长乘积的一半。

希望上面对菱形知识点的总结学习，同学们都能很好的掌握，相信同学们一定能很好的参加考试工作。

初中数学知识点总结:平面直角坐标系
下面是对平面直角坐标系的内容学习，希望同学们很好的掌握下面的内容。

小学菱形知识点总结归纳
一、菱形的定义
菱形是一个特殊的四边形，它具有以下特点：
1. 所有四条边相等；
2. 相对的两条边平行；
3. 相对的两个角相等；
4. 对角线相交于90度角。

在图形上，菱形通常用菱形符号（♦）来表示。

二、菱形的性质
1. 对角线相等：菱形的两条对角线互相垂直且相等。

2. 内角和：菱形的内角和为360度，即每个角为90度。

3. 对角线的中点角：菱形的对角线交点处的各条边的中点构成的角均为90度角。

4. 对角线平分内角：菱形的对角线平分相对的两个内角。

三、菱形的计算
1. 计算菱形的面积：菱形的面积计算公式为A= d1 * d2 / 2，其中d1和d2分别为菱形的对角线的长度。

2. 计算菱形的周长：菱形的周长计算公式为P= 4 * a，其中a为菱形的边长。

四、菱形的应用
1. 几何题目：在数学课堂上，老师会出一些涉及菱形的几何题目，通过计算和推理来帮助学生掌握菱形的性质和应用。

2. 日常生活：在日常生活中，我们可以看到很多菱形的物体，比如菱形的地砖、菱形的邮票等。

了解菱形的性质有助于我们更好地理解这些物体的特点和结构。

总结：
小学阶段，学生需要掌握菱形的定义、性质、计算和应用。

通过理论学习和实际应用，帮助学生对菱形有更深入的理解和掌握。

掌握菱形的知识有助于培养学生的逻辑思维能力和几何直觉，为学习中学阶段的几何学打下坚实的基础。

菱形几何知识点总结一、菱形的定义菱形是一种特殊的四边形，具有以下几个特点：1. 四条边相等：菱形的四条边长都相等，记作AB=BC=CD=DA。

2. 对角线相等：菱形的两条对角线相等，记作AC=BD。

3. 对角相等：菱形的四个角都相等，每个角为90度。

二、菱形的性质1. 对角相等：菱形的四个角都是直角，即每个角都等于90度。

2. 对角线相交于垂直平分点：菱形的两条对角线在交点处互相垂直，并且将对角互相平分。

3. 相邻角互补：菱形的相邻角之和等于180度。

例如角A+角B=180度，角B+角C=180度等。

这是因为菱形的相邻角是对角。

4. 边相等：菱形的四条边都相等。

5. 对角线的长度：菱形的对角线长度相等，即AC=BD。

6. 等腰梯形：两对相邻的边相等，所以菱形也是一个等腰梯形。

三、菱形的相关定理1. 相反角相等定理：在菱形中，对角相等。

2. 对角线平分相交角定理：菱形的对角线平分相交角。

3. 对角线长度相等定理：在菱形中，对角线相等。

4. 菱形的边平分角定理：菱形的对角线相交的交点平分菱形的各个顶角。

5. 菱形的角平分边定理：在菱形中，菱形的对角线平分菱形的各个角。

通过掌握以上定理，我们可以更好地理解和运用菱形的相关知识。

四、菱形的相关例题下面我们通过一些例题来练习和应用菱形的相关知识。

例题1：在菱形ABCD中，AC=6cm，BD=8cm，求菱形ABCD的周长。

解：由于菱形的所有边长相等，所以菱形ABCD的周长为4*6=24cm。

例题2：在菱形ABCD中，AC=10cm，角A=60度，求菱形ABCD的面积。

解：由于菱形的对角相等，所以菱形ABCD的面积可以通过角A的三角函数求得，设菱形ABCD的对角为2θ，其中θ=30度，则菱形ABCD的面积为S=AC^2*sinθ*cosθ=100cm^2。

例题3：在菱形ABCD中，AC=6cm，对角线BD=8cm，求菱形ABCD的面积。

解：根据菱形的对角线长度相等定理，对于菱形ABCD，AC=BD=8cm，所以菱形ABCD的面积为S=AC*BD/2=24cm^2。

菱形的判定知识点总结一、菱形的定义菱形是一种四边形，具有以下特征：1. 四条边长相等：菱形的四条边的长度都相等。

2. 对角线相等：菱形的两条对角线的长度相等。

3. 相对角相等：菱形的相对角也相等。

根据菱形的定义，我们可以使用这些特征来判定一个四边形是否为菱形。

二、菱形的判定方法1. 根据边长判定：如果一个四边形的四条边长都相等，那么它就是一个菱形。

例如，如果一个四边形的四条边的长度分别为a，a，a，a，则可以判定为菱形。

2. 根据对角线判定：如果一个四边形的对角线长度相等，那么它就是一个菱形。

例如，如果一个四边形的对角线的长度分别为d，d，则可以判定为菱形。

3. 根据边长和对角线判定：如果一个四边形的四条边长相等且对角线长度相等，那么它就是一个菱形。

例如，如果一个四边形的四条边的长度分别为a，a，a，a，且对角线的长度分别为d，d，则可以判定为菱形。

除了以上方法外，学生还需要掌握菱形的性质以及相关的定理。

以下是菱形的一些性质和定理：1. 菱形的对角线互相垂直：菱形的对角线互相垂直，并且将菱形分成四个全等的直角三角形。

这个性质对于理解菱形的形状和结构非常重要。

2. 菱形的对边平行：菱形的对边是平行的。

这个性质可以帮助我们证明菱形的性质和定理，以及解决相关的几何问题。

3. 菱形的对角线角平分：菱形的对角线将菱形的内角平分。

这个性质可以帮助我们证明菱形的内角之间的关系，并且解决相关的角平分问题。

4. 菱形的内角和为360度：菱形的四个内角的和为360度。

这个定理可以帮助我们计算菱形的内角之和，并且解决相关的角度问题。

通过掌握菱形的定义、判定方法、性质和定理，学生可以更好地理解和掌握菱形的知识，并且能够运用这些知识解决相关的几何问题。

因此，学生在学习菱形的过程中，应该注重理解和掌握菱形的定义和特征，练习菱形的判定方法，掌握菱形的性质和定理，以及解决相关的几何问题。

通过不断地练习和应用，学生可以更好地掌握菱形的知识，并且在考试中取得更好的成绩。

八年级菱形的性质知识点
菱形是一种特殊的四边形，其中所有边的长度相等，对角线相互垂直且长度相等。

在八年级的学习中，菱形的性质是不可避免的一部分。

下面将介绍八年级菱形的性质知识点。

一、菱形的定义
菱形是一种四边形，其四条边长度相等。

又称为矮胖子、斜方形。

二、菱形的性质
1. 对角线垂直
菱形的两条对角线互相垂直，也就是说，对角线相交的角度为90度。

2. 对角线相等
菱形的两条对角线相等，即AC=BD。

3. 平行四边形的性质
菱形的两个对角线将其分成两个直角三角形，这两个直角三角
形是相似的，并且它们分别与菱形三个顶点连成的三角形相似。

另外，如果菱形的两个对角线在顶点处相交，则该菱形是一个
正方形。

4. 对顶角
菱形的四个内角分别为90度、90度、90度和90度，也就是说，菱形的相邻两角和为180度。

三、菱形的应用
1. 计算菱形的面积
菱形的面积可以通过以下公式计算：
面积=对角线 1 ×对角线 2 ÷2
例如，如果菱形的对角线长分别为6厘米和8厘米，那么它的面积为6×8÷2=24平方厘米。

2. 解决几何问题
在许多几何问题中，我们需要使用到菱形的性质。

例如，我们需要计算汽车运动时的最短路径，或者掌握一些建筑物的特殊设计。

四、结论
菱形是一种特殊的四边形，其对角线相互垂直且长度相等。

在八年级菱形的学习中，我们必须掌握其性质，以便能够解决许多几何问题。

此外，菱形还具有漂亮的外观，因此在建筑和工业设计中，它们经常被用来作为特殊形状的元素。

人教版八年级菱形知识点归纳很实用
人教版八年级菱形知识点归纳
本文档总结了人教版八年级数学中与菱形相关的知识点，帮助学生更好地理解和掌握该内容。

1. 菱形的定义和特点
- 菱形的定义：具有四条边相等且两两相交于4个顶点的四边形。

- 菱形的特点：
- 对角线相互垂直；
- 对角线相等；
- 每个内角都是直角。

2. 菱形的性质
- 外接圆性质：
- 菱形的四个顶点在一个圆上；
- 外接圆的半径等于菱形对角线的一半。

- 内切圆性质：
- 菱形的内切圆的圆心和菱形的重心重合；- 内切圆的半径等于菱形一条边的一半。

- 长菱形与短菱形：
- 长菱形：对角线一长一短；
- 短菱形：对角线相等。

- 菱形的面积计算：
- 面积等于对角线的乘积的一半。

3. 菱形相关的公式
- 设菱形边长为a，对角线长度为d：
- 面积公式：S = (d1 * d2) / 2
- 周长公式：P = 4a
4. 菱形的解题技巧
- 根据菱形的对称性质简化解题步骤；
- 利用菱形的性质求解问题；
- 注意计算时保持准确性和精度。

以上是人教版八年级数学中与菱形相关的知识点归纳。

希望对学生们的研究有所帮助。

数学菱形判定知识点总结一、菱形的定义菱形是一种特殊的四边形，它具有以下特点：1. 四边相等：菱形的四条边长度相等。

2. 对角线相等：菱形的对角线长度相等。

3. 对角线垂直：菱形的对角线互相垂直。

4. 相邻角互补：菱形的相邻角互补，即相邻的两个角的和为180°。

二、菱形的判定方法1. 利用对角线判定菱形：如果一个四边形的对角线相等，则这个四边形是菱形；即AC=BD，则ABCD为菱形。

2. 利用边长判定菱形：如果一个四边形的四边相等，则这个四边形是菱形；即AB=BC=CD=DA，则ABCD为菱形。

3. 利用角度判定菱形：如果一个四边形的相邻角互补且对角线相等，则这个四边形是菱形；即∠A+∠B=∠B+∠C=∠C+∠D=∠D+∠A=180°，并且AC=BD，则ABCD为菱形。

三、菱形的性质1. 对角线垂直：菱形的对角线互相垂直；即AC⊥BD。

2. 对角线平分：菱形的对角线互相平分；即AC=BD。

3. 角性质：菱形的内角为90°；即∠A=∠B=∠C=∠D=90°。

4. 边长性质：菱形的四边相等；即AB=BC=CD=DA。

四、菱形的应用1. 解题方法：在解题过程中，如果遇到了菱形的相关问题，可以根据菱形的判定方法和性质来解答。

通过判定四边形是否满足菱形的条件，再根据菱形的性质进行推理和计算，从而得出答案。

2. 几何证明：在几何证明中，菱形的性质和判定方法经常被应用。

可以利用菱形的对角线垂直、对角线平分等性质，来推导出与菱形相关的定理和结论。

3. 建模应用：菱形作为一种特殊的几何图形，在建模过程中也有着特殊的应用。

例如在建筑、设计等领域中，可以利用菱形的性质和特点来构建特定的结构和图案。

五、拓展延伸菱形是一种特殊的四边形，它的性质和应用涉及到了数学的多个知识点。

在学习菱形的基础上，可以进一步拓展延伸相关的数学知识，例如平行四边形、矩形、正方形等特殊的四边形，从而更好地理解和运用几何知识。

菱形知识点总结及典型试题知识点一：菱形的定义：一组邻边相等的平行四边形叫做菱形。

知识点二：菱形的性质：①具有平行四边形的一切性质；①菱形的四条边都相等；①菱形的两条对角线互相垂直,并且每一条对角线平分一组对角；①菱形既是中心对称图形又是轴对称图形，对称中心是两条对角线的交点，对称轴是对角线所在的直线。

知识点三：.菱形的判定方法：①有一组邻边相等的平行四边形是菱形；①对角线互相平分且垂直的四边形是菱形；①对角线互相垂直的平行四边形是菱形；④四条边都相等四边形是菱形；每条对角线平分一组对角的四边形是菱形。

14.有关菱形面积的计算：①由于菱形的对角线互相垂直平分,11()22ABD CBDS S S BD OA OC BD AC ∆=+=+=⋅；①也可以用平行四边形的面积计算公式=底⨯高。

典型试题一．选择题（共9小题）1．如图，在菱形ABCD中，∠A=60°，E，F分别是AB，AD的中点，DE，BF相交于点G，连接BD，CG，有下列结论：①∠BGD=120°；②BG+DG=CG；③∠BDF∠∠CGB．其中正确的结论有（）A．0个B．1个C．2个D．3个2．如图，菱形ABCD的边长为1，BD=1，E，F分别是边AD，CD上的两个动点，且满足AE+CF=1，设∠BEF的面积为s，则s的取值范围是（）A.1/4≤s≤1B.3√3/4≤s≤√3C.3√3/16≤s≤ √3/4D.3√3/8≤s≤ /2√33．如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC=∠BEF=60°，则PG/PC==（）A.√2 B.√3 C.√2/2 D.√3/3 5．如图，在菱形ABCD中，∠A=110°，E，F分别是边AB和BC的中点，EP∠CD于点P，则∠FPC=（）A．35° B．45° C．50° D．55°1．7．如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP∠CD于点P，则∠FPC=（）A．35° B．45° C．50° D．55°8．如图，在菱形ABCD中，若∠B=60°，点E、F分别在AB、AD上，且BE=AF，则∠AEC+∠AFC 的度数等于（）A．120° B．140° C．160° D．180°9．如图，边长为1的菱形ABCD中，∠DAB=60°．连结对角线AC，以AC为边做第二个菱形ACEF，∠FAC=60°．连结AE，再以AE为边做第三个菱形AEGH，使∠HAE=60°…按此规律所作的第2014个菱形的边长是（）A.(√3)2012 B.(√3)2013 C.(√3)2014 D.(√3)201510．如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为（）A.2√3B.3√3C.6√3 9√3/211.如图，两个连接在一起的菱形的边长都是1cm，一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行，当电子甲虫爬行2014cm时停下，则它停的位置是（）A．点F B．点E C．点A D．点C12．如图，菱形ABCD的边长为4，过点A、C作对角线AC的垂线，分别交CB和AD的延长线于点E、F，AE=3，则四边形AECF的周长为（）A．22 B．18 C．14 D．11二．填空题（共21小题）1．如图，菱形ABCD中，E、F分别是BC、CD的中点，过点E作EG∠AD于G，连接GF．若∠A=80°，则∠DGF的度数为．2．如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒∠DEF为等边三角形，则t的值为.3．如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将∠AMN沿MN所在直线翻折得到∠A′MN，连接A′C，则A′C长度的最小值是4．如图，在Rt∠ABC中，∠ACB=90°，AC=BC=6cm，点P从点A出发，沿AB方向以每秒√2 cm 的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将∠PQC沿BC翻折，点P的对应点为点P′，设Q点运动的时间为t秒，若四边形QPCP′为菱形，则t的值为.5．如图，已知菱形ABCD，E、F分别为AB、BC的中点，EP∠DC，垂足为P，连接PF，若∠A=110°，则∠FPC= ．6．如图，边长为1的菱形ABCD中，A在原点，B在x轴正半轴上，∠DAB=60°．连接对角线AC，以AC为边作第二个菱形ACC1D1，∠D1AC=60°；连接AC1，再以AC2为边作第三个菱形AC1C2D2，使∠D2AC1=60°，…，C、C1、C2、C3…按逆时针方向排列，按此规律所作的第2015个菱形AC2013C2014D2014的顶点C2014的坐标为.7．如图，菱形OABC的面积为3√3，顶点O的坐标为（0，0），顶点A的坐标为（3，0），顶点B在第一象限，边BC与y轴交于点D，点E在边OA上．将四边形ABDE沿直线DE翻折，使点A落在这个坐标平面内的点F处，且AE∠EF．则点F的坐标为.8．如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF，若菱形ABCD的边长为2cm，∠A=120°，则EF= cm．9．如图，四边形ABCD与四边形AEFG都是菱形，其中点C在AF上，点E，G分别在BC，CD上，若∠BAD=135°，∠EAG=75°，则AB/AE= .10．如图，菱形ABCD的顶点分别在x轴或y轴上，物体甲和物体乙分别由点A（2，0）同时出发，沿菱形ABCD的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以3个单位/秒匀速运动，则两个物体运动后的第2013次相遇地点的坐标是．11．如图，将正∠ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小三角形，若m/n =47/25 ，则∠ABC的边长是．12．如图，将两张长为4，宽为1的矩形纸条交叉并旋转，使重叠部分成为一个菱形．旋转过程中，当两张纸条垂直时，菱形周长的最小值是4，那么菱形周长的最大值是. 13．如图，已知菱形ABCD的边AB=10，对角线BD=12，BD边上有2012个不同的点P1，P2，…，P2012，过Pi（i=1，2，…，2012）作P i E i∠AB于E i，P i F i∠AD于F i，则P1E1+P1F1+P2E2+P2F2+…+P2012E2012+P2012F2012的值为.14．如图，在菱形ABCD中，已知E、F分别是边AB、BC的中点，CE、DF交于点G．若∠CGF 的面积为2，则菱形ABCD的面积为．15．如图①，在菱形ABCD中，AD=BD=1，现将∠ABD沿AC方向向右平移到∠A1B1D1的位置，得到图②，则阴影部分的周长为．16．如图，在一个内角为60°的菱形ABCD中，边长为4，将它绕点O顺时针旋转90°后得到菱形A′B′C′D′，则阴影部分的周长为.17．已知直线AB交平面直角坐标系xOy两坐标轴的A（10，0）、B（0，5）两点，在直线AB上有一动点M，在坐标系内有另一点N，若以点O、B、M、N为顶点构成的四边形为菱形，则点N的坐标为.18．如图，菱形ABCD的周长为16，以AB为一边画等边∠ABE，点E、D在直线AB的同侧，在AC上找一点P，使EP+DP最小，则这个最小值为．19．如图，在菱形ABCD中，对角线AC、BD相交于点O，且AC=12，BD=16，E为AD的中点，点P在BD上移动，若∠POE为等腰三角形，则所有符合条件的点P共有个．20．如图所示，两个全等菱形的边长为1米，一个微型机器人由A点开始按A-＞B-＞C-＞D-＞E-＞F-＞C-＞G-＞A的顺序沿菱形的边循环运动，行走2009米停下，则这个微型机器人停在点．21．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为．22．如图在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2014次，点B的落点依次为B1，B2，B3，则B2014的坐标为。